Segmentotopes

• Segmentotopes
• Convex Segmentochora
  • Cases with Tetrahedral Axis
  • Cases with Octahedral Axis
  • Cases with Icosahedral Axis
  • Cases with n-Prismatic or n-Antiprismatic Axis
  • Non-Lace-Prismatics
  • Complete Table
  • Close Relatives
  • Further Reading
• Convex Segmentotera

In 2000 Klitzing published^[1] on segmentotopes in general resp. his research on convex segmentochora in special. Segmentotopes are polytopes which bow to the following conditions:

• all vertices on the surface of 1 hypersphere
• all vertices on 2 parallel hyperplanes
• all edges of 1 length

The first condition shows that the circumradius is well defined. Moreover, in union with condition 3 this implies that all 2D faces have to be regular. The sandwich type 2nd condition implies that all edges, which aren't contained completely within one of the hyperplanes, would join both, i.e. having one vertex each in either plane. Thence segmentotopes have to be monostratic. In fact, segmentotopes are the monostratic orbiforms. (Orbiforms, a terminus which had been created several years later only, just use the first and third condition of those.) Finally it follows, that the bases have to be orbiforms, while all the lacing elements have to be (lower dimensional) segmentotpes.

The naming of individual segmentotopes usually is based on the 2 base polytopes: top-base polytope atop bottom-base polytope. Symbolically one uses the parallelness of those bases: P_top || P_bottom. (For the smaller segmentotopes the choice of bases need not be unique.)

Segmentotopes are closely related to lace prisms. In fact those concepts have a large common intersection, but they are not identical. While lace prisms need an axis of symmetry (in fact one which is describable as Dynkin symbol), one uses the terminus "axis" in the context of segmentotopes only in the sense of the line defined by the centers of the circumspheres of d-1 dimensional bases. (Thus the topic of axial polytopes does more relate to lace towers (as multistratic generalizations of lace prisms) than to segmetotopes. None the less there is a large overlap.) – Note that the radius R of the d-1 dimensional circumsphere used for a segmentotpal base of dimension d-k might well be larger than the radius r of its d-k dimensional circumsphere: for k > 1 the latter might well be placed within the former with some additional shift s:   R² = r² + s². For a simple example just consider squippy, the 4-fold pyramid, which is just half of an oct, when being considered as line || triangle: the subdimensional base, the single edge, there is placed off-set.

Convex Segmentochora

Just as polytopes are distinguished dimensionally as polygons, polyhedra, polychora, etc. so too are segmentotopes.
The only segmentogons (without any further adjectivic restriction) clearly are
- regular triangle   (point || line) and
- square   (line || line).
Segmentohedra already include infinite series like
- pyramids   (base being 2 < n/d < 6:   point || {n/d}),
- prisms   (bases being 2 < n/d:   {n/d} || {n/d}),
- antiprisms and retroprisms   (bases being 2 < n/d resp. 3/2 < n/d < 2:   {n/d} || {n/(n-d)}),
- cupolae and cuploids(*)   (top base being 6/5 < n/d < 6, d odd resp. even:   {n/d} || {2n/d}),
- cupolaic blends(*)   (top base being 6/5 < n/d < 6, d odd:   ( {2n/d}[2{n/d}]{2n/d} ) || {4n/2d}).
(*) Grünbaumian bottom base understood to be withdrawn.
For convex ones d clearly has to be 1 and several of the above series then become finite.

Polychora generally have the disadvantage not being visually accessible. Segmentochora are not so hard for that: Just consider the 2 base polyhedra displayed concentrically, perhaps slightly scaled, while the lacings then get slightly deformed. Mathematically speaking, axial projections (view-point at infinity) and central projections (finite view-point), either one being taken on the axis for sure, from 4D onto 3D generally are well "viewable" for such monostratic figures. Especially when using real 3D graphics (like the here used VRMLs) instead of further projections onto 2D as in usual pictures: Note that all pictures at "segmentochoron display" within individual polychoron files will be linked to such VRML files.

Cases with Tetrahedral Axis:

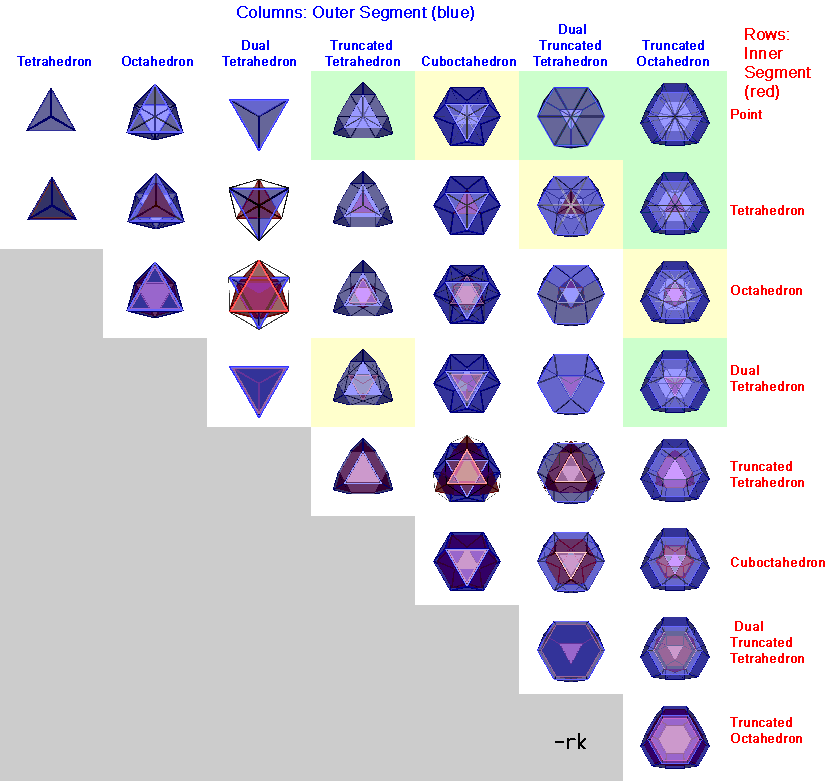
Cases with Octahedral Axis:

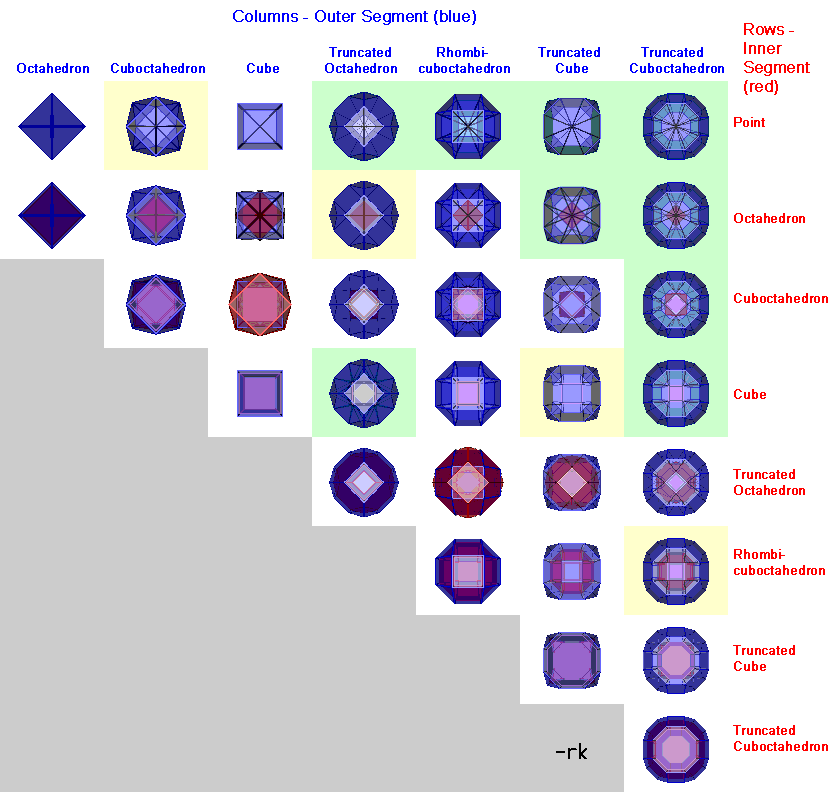
Cases with Icosahedral Axis:

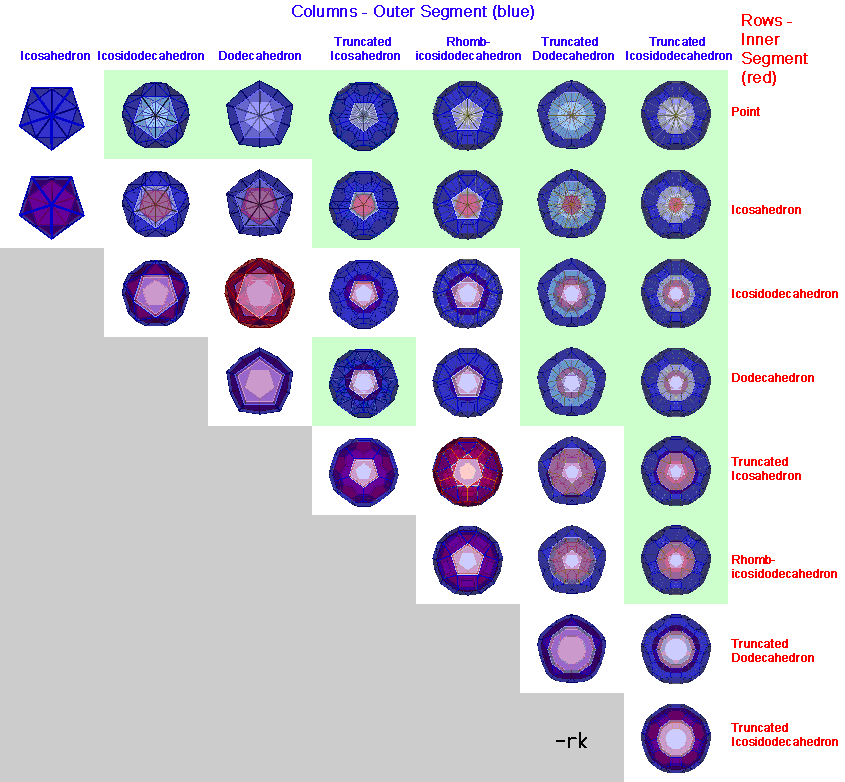
Cases with n-Prismatic or n-Antiprismatic Axis:

Non-Lace-Prismatics:

Just as used within Johnson solids several of the above segmentochora allow diminishings. Those generally break some symmetries of one or both bases, and therefore too of the axial symmetry. Thus there is no longer a unifying symmetry according to which a Dynkin symbol could be designed, being the premise for lace prisms. Even so, such diminished ones are fully valid segmentotopes (following the above 3 conditions). An easy 3D example could be again line || triangle, the alternate description of the above mentioned squippy. The easiest 4D one clearly is squippypy (i.e. a 1/4 of the hex). – Gyrations in some spare cases might apply as well, even so those in general would conflict to the requirement of exactly 2 vertex layers.

But there is also a generic non-lace-prismatic convex segmentochoron with octahedral symmetry at one base, with icosahedral symmetry at the other. (The common subsymmetry clearly is the pyrital. But that one does not bow to Dynkin symbol description.) That one uses as faces 1 cube (as bottom base), 6 trip (as line || square), 12 squippy (as triangle || line), 8 tet (as triangle || point), and 1 ike (as top base).

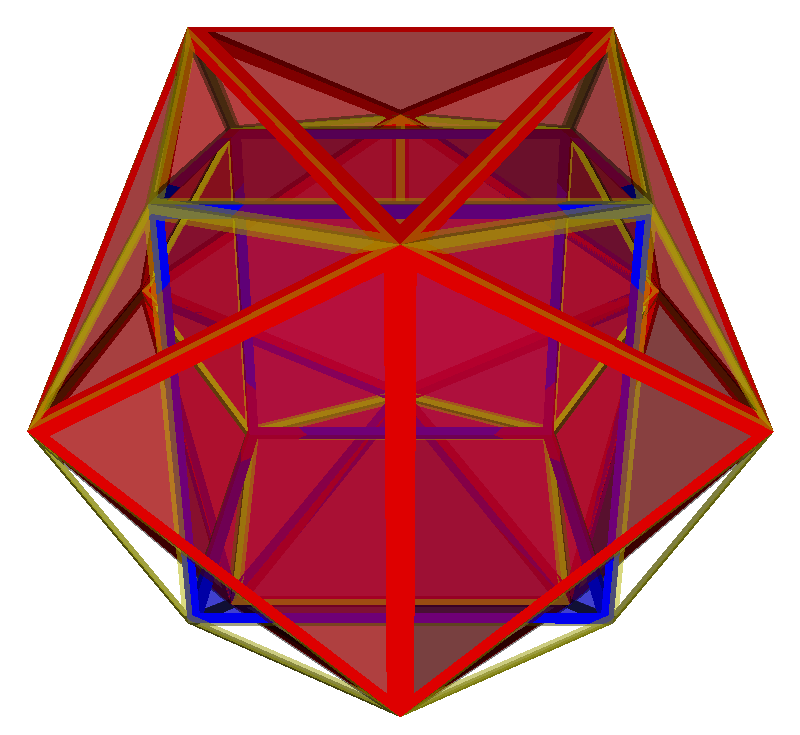
Full Table:

K-4.1   pt || tet
K-4.1.1 line || perp {3}

K-4.2   tet || dual tet

K-4.3   pt || oct
K-4.3.1 {3} || gyro tet

K-4.4   pt || squippy
K-4.4.1 line || tet
K-4.4.2 {3} || incl {3}
K-4.4.3 line || perp {4}

K-4.5   tet || oct

K-4.6   tet || squippy
K-4.6.1 {3} || oct
K-4.6.2 {3} || gyro trip

K-4.7   line || squippy
K-4.7.1 {3} || tet
K-4.7.2 pt || trip
K-4.7.3 {3} || otho {4}
   (where 1 {3}-edge || 2 {4}-edges)

K-4.8   {3} || squippy
K-4.8.1 {4} || tet
K-4.8.2 line || ortho trip

K-4.9   tet || tet
K-4.9.1 line || para trip
K-4.9.2 {4} || ortho {4}

K-4.10   {3} || trip

K-4.11   oct || oct
K-4.11.1 trip || gyro trip

K-4.12   squippy || squippy
K-4.12.1 {4} || trip
K-4.12.2 line || cube

K-4.13   trip || refl ortho trip

K-4.14   {4} || squap
K-4.14.1 {4} || gyro cube

K-4.15   oct || cube

K-4.16   squippy || gyro cube

K-4.17   {4} || gyro squippy
K-4.17.1 pt || squap

K-4.18   trip || trip
K-4.18.1 {4} || cube

K-4.19   squap || squap
K-4.19.1 cube || gyro cube

K-4.20   cube || cube

K-4.21   cube || ike

K-4.22   {5} || pap
K-4.22.1 {5} || gyro pip

K-4.23   tet || co

K-4.24   tet || tricu

K-4.25   {3} || tricu
K-4.25.1 {6} || trip

K-4.26   {4} || squippy
K-4.26.1 pt || cube

K-4.27   {3} || gyro tricu
K-4.27.1 {6} || oct

K-4.28   {4} || co

K-4.29   oct || co

K-4.30   oct || tricu

K-4.31   squippy || co

K-4.32   squippy || tricu

K-4.33   {3} || teddi

K-4.34   {5} || pip

K-4.35   cube || co

K-4.36   ike || ike

K-4.37   gyepip || gyepip

K-4.38   peppy || peppy
K-4.38.1 line || pip

K-4.39   pap || pap
K-4.39.1 pip || gyro pip

K-4.40   mibdi || mibdi

K-4.41   teddi || teddi

K-4.42   pip || pip

K-4.43   co || co

K-4.44   tobcu || tobcu

K-4.45   tricu || tricu
K-4.45.1 trip || hip

K-4.46   {6} || hap
K-4.46.1 {6} || gyro hip

K-4.47   {6} || hip

K-4.48   co || tut

K-4.49   tobcu || tut

K-4.50   tricu || tut

K-4.51   {6} || tricu
K-4.51.1 {3} || hip

K-4.52   oct || tut

K-4.53   hap || hap
K-4.53.1 hip || gyro hip

K-4.54   hip || hip

K-4.55   tut || inv tut

K-4.56   tet || tut

K-4.57   tut || tut

K-4.58   {8} || oap
K-4.58.1 {8} || gyro op

K-4.59   {8} || op

K-4.60   snic || snic

K-4.61   co || sirco

K-4.62   co || escu

K-4.63   co || op

K-4.64   {4} || gyro squacu
K-4.64.1 {8} || squap

K-4.65   oap || oap
K-4.65.1 op || gyro op

K-4.66   sirco || sirco

K-4.67   gyesquibcu || gyesquibcu

K-4.68   escu || escu

K-4.69   squacu || squacu
K-4.69.1 cube || op

K-4.70   op || op

K-4.71   cube || sirco

K-4.72   cube || gyesquibcu

K-4.73   {4} || squacu
K-4.73.1 {8} || cube

K-4.74   doe || doe

K-4.75   sirco || toe

K-4.76   tut || toe

K-4.77   doe || id

K-4.78   ike || doe

K-4.79   gyepip || doe

K-4.80   {5} || gyro peppy
K-4.80.1 pt || pap

K-4.81   pap || doe

K-4.82   mibdi || doe

K-4.83   teddi || doe

K-4.84   pt || ike

K-4.85   pt || gyepip

K-4.86   pt || peppy
K-4.86.1 line || perp {5}

K-4.87   pt || mibdi

K-4.88   pt || teddi

K-4.89   toe || toe

K-4.90   id || id

K-4.91   pobro || pobro

K-4.92   pero || pero

K-4.93   {10} || dap
K-4.93.1 {10} || gyro dip

K-4.94   {10} || dip

K-4.95   co || toe

K-4.96   dap || dap
K-4.96.1 dip || gyro dip

K-4.97   dip || dip

K-4.98   toe || tic

K-4.99    tic || tic

K-4.100   sirco || tic

K-4.101   esquigybcu || tic

K-4.102   sirco || gyro tic

K-4.103   escu || tic

K-4.104   escu || gyro tic

K-4.105   {8} || squacu
K-4.105.1 {4} || op

K-4.106   op || tic

K-4.107   oct || sirco

K-4.108   squippy || escu

K-4.109   squippy || squacu

K-4.110   snid || snid

K-4.111   srid || srid

K-4.112   gyrid || gyrid

K-4.113   pabgyrid || pabgyrid

K-4.114   mabgyrid || mabgyrid

K-4.115   tagyrid || tagyrid

K-4.116   dirid || dirid

K-4.117   pecu || pecu
K-4.117.1 pip || dip

K-4.118   pagydrid || pagydrid

K-4.119   magydrid || magydrid

K-4.120   bagydrid || bagydrid

K-4.121   pabidrid || pabidrid

K-4.122   mabidrid || mabidrid

K-4.123   gybadrid || gybadrid

K-4.124   tedrid || tedrid

K-4.125   girco || girco

K-4.126   srid || ti

K-4.127   ti || ti

K-4.128   tic || girco

K-4.129   co || tic

K-4.130   tid || tid

K-4.131   id || srid

K-4.132   id || drid

K-4.133   {5} || gyro pecu
K-4.133.1 {10} || pap

K-4.134   id || pabidrid

K-4.135   id || mabidrid

K-4.136   id || tedrid

K-4.137   ike || id

K-4.138   gyepip || id

K-4.139   peppy || pero

K-4.140   gyepip || pero

K-4.141   {5} || peppy
K-4.141.1 pt || pip

K-4.142   pap || id

K-4.143   mibdi || id

K-4.144   pap || pero

K-4.145   mibdi || pero

K-4.146   {5} || pero

K-4.147   teddi || id

K-4.148   teddi || pero

K-4.149   toe || girco

K-4.150   grid || grid

K-4.151   ti || tid

K-4.152   doe || srid

K-4.153   doe || drid

K-4.154   {5} || pecu
K-4.154.1 {10} || pip

K-4.155   doe || pabidrid

K-4.156   doe || mabidrid

K-4.157   doe || tedrid

K-4.158   id || ti

K-4.159   srid || tid

K-4.160   gyrid || tid

K-4.161   pabgyrid || tid

K-4.162   mabgyrid || tid

K-4.163   tagyrid || tid

K-4.164   drid || tid

K-4.165   {10} || pecu
K-4.165.1 {5} || dip

K-4.166   pagydrid || tid

K-4.167   magydrid || tid

K-4.168   bagydrid || tid

K-4.169   pabidrid || tid

K-4.170   mabidrid || tid

K-4.171   gybadrid || tid

K-4.172   tedrid || tid

K-4.173   tid || grid

K-4.174   {n} || n-ap
K-4.174.1 {n} || gyro n-p

K-4.175   {n} || n-p

K-4.176   n-ap || n-ap
K-4.176.1 n-p || gyro n-p

K-4.177   n-p || n-p

Close Relatives:

1. In 2012 two sets of closely related monostratic polytopes where found:

   • n-py || inv gyro n-py   (2<n<6)   and
   • n-cu || inv gyro n-cu   (6/5<n<6).

   In fact the constraint, of the lacing edges all having unit lengths too, results in some specific shift values for the base polyhedra. As those base polyhedra on the other hand are not degenerate, this conflicts to having a common circumsphere in general: within the case of pyramids only the special value n=3 results in a true convex segmentochoron (being the hex), within the case of cupolae only the special value n=2 results in a true convex segmentochoron (being trip || refl ortho trip). Even so, the values n=3,4,5 resp. n=2,3,4,5 would well generate monostratic convex regular-faced polychora (CRFs).

   The closeness even could be pushed on a bit. If one of the (equivalent) bases each, which are segmentohedra in turn, would be diminished by omitting the smaller top face, i.e. maintaining therefrom only the larger bottom face, those would re-enter the range of valid segmentochora again: {n} || gyro n-py resp. {2n} || n-cu. In fact, here the necessary shifts of the bases could be assembled at the degenerate base alone. There a non-zero shift is known to be allowed.

   Without narrowing those findings, those 2 families could be de-mystified a bit by using different axes: the pyramidal case is nothing but the bipyramid of the n-antiprism, while the cupolaic case is nothing but the bistratic lace tower xxo-n-oxx oxo&#xt.

2. Besides of considering 2 parallel hyperplanes cutting out monostratic layers of larger polychora, in 2012 (and more deeply in 2013) considerations about 2 intersecting equatorial hyperplanes were done. Those clearly cut out wedges. The specific choice of those hyperplanes made up the terminus lunae. Only the CRF ones were considered. The following lunae are known so far:

   • Lunae of hex: cells being squippy and tet
     • 1/4-luna of hex = squippypy = pt || squippy (thus a segmentochoron) – hyperplanes intersect at 90°.
   • Lunae of ico: cells being tricu, oct, and squippy
     • 2/6-luna of ico = oct || tricu (thus a segmentochoron) – hyperplanes intersect at 120°.
     • 1/6-luna of ico = {3} || gyro tricu (thus a segmentochoron) – hyperplanes intersect at 60°.
   • Lunae of ex: cells being pero, peppy, and tet
     • 4/10-luna of ex – hyperplanes intersect at 144°.
     • 3/10-luna of ex – hyperplanes intersect at 108°.
     • 2/10-luna of ex – hyperplanes intersect at 72°.
     • 1/10-luna of ex – hyperplanes intersect at 36°.

3. Surely the convexity restriction could be released. Some 3D examples can be found on the page on axials. A quite immediate 4D case could be e.g. gikepy.

Further Reading

• ↑ Convex Segmentochora – (PDF)
  published as: "Convex Segmentochora", by Dr. R. Klitzing, Symmetry: Culture and Science, vol. 11, 139-181, 2000
• external link (hosted by J. McNeill)

----
 5D
----

(Just some) Convex Segmentotera

hix =  pt || pen
hix =  line || ortho tet
hix =  {3} || ortho {3}

tac =  pen || dual pen

hexpy =  pt || hex (segment of tac)

line || ortho oct (segment of tac)

{3} || ortho {4} (segment of tac)

hin =  hex || gyro hex

rappy =  pt || rap (segment of hin)

tet || inv tepe (segment of hin)

pen || inv rap (segment of hin)

oct || hex (bidiminishing of hin)
tet || rap (bidiminishing of hin)

penp =  pen || pen

rix =  pen || rap

pt || tepe (segment of rix)

oct || tepe (segment of rix)

{3} || triddip (segment of rix)

tratet =  tet || tepe
tratet =  {3} || triddip
tratet =  trip || lacing-ortho trip

hexip =  hex || hex

dot =  rap || inv rap

pt || triddip (segment of dot)

tet || ope (segment of dot)

troct =  oct || ope
troct =  triddip || gyro triddip

rappip =  rap || rap
rappip =  ope || tepe

trip || tisdip (segment of rappip)

squatet =  tepe || tepe
squatet =  {4} || tisdip
squatet =  cube || lacing-ortho cube

tratrip =  trip || tisdip
tratrip =  triddip || triddip

squoct =  ope || ope
squoct =  tisdip || {3}-gyro tisdip

hex || ico (segment of rat)

rap || spid (segment of rat)

pt || ope (segment of rat)

pen || spid (segment of scad)

tracube =  cube || tes
tracube =  tisdip || tisdip

petet =  {5} || trapedip
petet =  pip || lacing-ortho pip

poct =  trapedip || {3}-gyro trapedip

trike =  ike || ipe

pent =  tes || tes

icope =  ico || ico

spiddip =  spid || spid

trapedippip =  pip || squipdip
trapedippip =  trapedip || trapedip

traco =  co || cope

hatet =  {6} || thiddip
hatet =  hip || lacing-ortho hip

squike =  ipe || ipe

rap || srip (segment of spix)

spid || srip (segment of spix)

tet || cope (segment of spix)

pecube =  squipdip || squipdip

hoct =  thiddip || {3}-gyro thiddip

squaco =  cope || cope

ico || rit (segment of nit)

rap || srip (segment of nit)

srip || inv srip (segment of nit)

oct || cope (segment of nit)

pt || tisdip (segment of nit)

srippip =  srip || srip

rap || tip (segment of sarx)

srip || tip (segment of sarx)

co || tuttip (segment of sarx)

{3} || thiddip (segment of sarx)

tratut =  tut || tuttip

hacube =  shiddip || shiddip

rittip =  rit || rit

tippip =  tip || tip

squatut =  tuttip || tuttip

pen || tip (segment of rin)

tip || deca (segment of rin)

srip || deca (segment of sibrid)

otet =  {8} || todip
otet =  op || lacing-ortho op

owoct =  todip || {3}-gyro todip

decap =  deca || deca

trasirco =  sirco || sircope

tradoe =  doe || dope

ocube =  sodip || sodip

squasirco =  sircope || sircope

sidpithip =  sidpith || sidpith (segment of scant)

squadoe =  dope || dope

rit || thex (segment of sirhin)

prip || tip (segment of cappix)

hiddip || triddip (segment of card)

prip || inv prip (segment of card)

prip || srip (segment of card)

thexip =  thex || thex

tratoe =  toe || tope

prippip =  prip || prip

exip =  ex || ex

gappip =  gap || gap

sadip =  sadi || sadi

trid =  id || iddip

squatoe =  tope || tope

ico || thex (segment of sart)

rico || thex (segment of sart)

prip || inv srip (segment of sart)

{3} || shiddip (segment of sart)

squid =  iddip || iddip

ricope =  rico || rico

grip || prip (segment of pattix)

tut || tope (segment of pattix)

tratic =  tic || ticcup

rico || rit (segment of spat)

prip || spid (segment of spat)

grippip =  grip || grip

squatic =  ticcup || ticcup

spiccup =  spic || spic

srittip =  srit || srit (segment of span)

sidpith || srit (segment of span)

deca || grip (segment of pirx)

tahp =  tah || tah

tattip =  tat || tat

srit || tat (segment of sirn)

rap || tip (segment of sirn)

sirco || ticcup (segment of sirn)

{4} || todip (segment of sirn)

rico || tah (segment of sibrant)

grip || srip (segment of sibrant)

co || tope (segment of sibrant)

gippiddip =  gippid || gippid

trasrid =  srid || sriddip

gippid || grip (segment of cograx)

squasrid =  sriddip || sriddip

tragirco =  girco || gircope

squagirco =  gircope || gircope

prittip =  prit || prit (segment of cappin)

trati =  ti || tipe

squati =  tipe || tipe

prohp =  proh || proh (segment of carnit)

prit || proh (segment of carnit)

prit || srit (segment of carnit)

hodip || tisdip (segment of carnit)

sricope =  srico || srico

ticope =  tico || tico

gippid || prip (segment of pattit)

proh || tat (segment of capt)

tah || tico (segment of pirt)

tratid =  tid || tiddip

grittip =  grit || grit (segment of prin)

squatid =  tiddip || tiddip

roxip =  rox || rox

grit || proh (segment of pattin)

tut || tuttip (segment of pattin)

contip =  cont || cont

pricope =  prico || prico

gidpithip =  gidpith || gidpith (segment of cogart)

hipe =  hi || hi

tragrid =  grid || griddip

squagrid =  griddip || griddip

gidpith || grit (segment of cogrin)

gricope =  grico || grico

rahipe =  rahi || rahi

thipe =  thi || thi

texip =  tex || tex

grixip =  grix || grix

gippiccup =  gippic || gippic

sidpixhip =  sidpixhi || sidpixhi

srixip =  srix || srix

srahip =  srahi || srahi

xhip =  xhi || xhi

prahip =  prahi || prahi

grahip =  grahi || grahi

3,n-dippip =  n-p || 4,n-dip
3,n-dippip =  3,n-dip || 3,n-dip

n,cube-dip =  4,n-dip || 4,n-dip

n,m-dippip =  n,m-dip || n,m-dip