|
Acronym
|
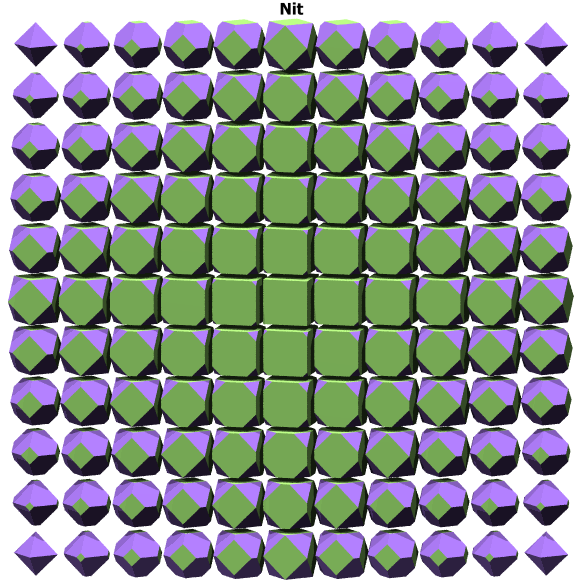
nit
|
|
Name
|
penteractitriacontiditeron,
birectified penteract,
birectified triacontiditeron,
birectified pentacross,
Gosset polytope 02,1,1,
equatorial cross-section of rat-first brag
|
|
Field of sections
|
 ©
|
|
Circumradius
|
sqrt(3/2) = 1.224745
|
Inradius
wrt. rap
|
3/sqrt(10) = 0.948683
|
Inradius
wrt. ico
|
1/sqrt(2) = 0.707107
|
|
Vertex figure
|
 ©  ©
|
Lace city
in approx. ASCII-art
|
o3x3o x3o3x o3x3o -- o3x3o4o (ico)
x3o3o x3x3o o3x3x o3o3x -- o3o3x4o (rit)
o3x3o x3o3x o3x3o -- o3x3o4o (ico)
\ \ \ \
\ \ \ +-- o3x3o3o (rap)
\ \ +------- x3o3x3o (srip)
\ +------------ o3x3o3x (inv. srip)
+----------------- o3o3x3o (inv. rap)
|
 ©
|
x3o4o o3x4o x3o4o -- o3x3o4o (ico)
o3x4o o3o4q o3x4o -- o3o3x4o (rit)
x3o4o o3x4o x3o4o -- o3x3o4o (ico)
|
(the yellow dots, taken alone, represent a vertex inscribed squaco)
|
Lace hyper city
in approx. ASCII-art
|
o3x
x3o x3o
x3x
o3x o3x
x3o
o3o
o3x o3x
o3u
x3x x3x
u3o
x3o x3o
o3o
o3x
x3o x3o
x3x
o3x o3x
x3o
(left to right -or- top to bottom: ico || rit || ico)
(upper-left front to lower-right back: rap || srip || inv. srip || inv. rap)
|
o4o x4o o4o
x4o o4q x4o
o4o x4o o4o
|
x4o o4q x4o
o4q o4q
x4o o4q x4o
|
o4o x4o o4o
x4o o4q x4o
o4o x4o o4o
|
(per layer: ico || rit || ico)
|
|
Coordinates
|
(1/sqrt(2), 1/sqrt(2), 1/sqrt(2), 0, 0) & all permutations, all changes of sign
|
|
Volume
|
31 sqrt(2)/10 = 4.384062
|
|
Surface
|
[60+11 sqrt(5)]/3 = 28.198916
|
|
General of army
|
(is itself convex)
|
|
Colonel of regiment
|
(is itself locally convex
– uniform polyteral members:
& others)
|
Dihedral angles
(at margins)
|
- at tet between rap and rap: arccos(-3/5) = 126.869898°
- at oct between ico and rap: arccos[-1/sqrt(5)] = 116.565051°
- at oct between ico and ico: 90°
|
|
Face vector
|
80, 480, 640, 280, 42
|
|
Confer
|
- uniform relative:
-
squaco
- related segmentotera:
-
rapasrip
sripa
coa tutcup
ica tutcup
icarit
tisdippy
octacope
coarit
squadinit
trial tricupe
octco tuttric
- related CRFs:
-
mibdinit
odnit
bodnit
- ambification:
-
sibrant
- ambification pre-image:
-
hin
- general polytopal classes:
-
Wythoffian polytera
lace simplices
partial Stott expansions
Coxeter-Elte-Gosset polytopes
- analogs:
-
birectified orthoplex brOn
birectified hypercube brCn
rectified Gossetic r(1n,2)
|
External
links
|
|
Incidence matrix according to Dynkin symbol
o3o3x3o4o
. . . . . | 80 ♦ 12 | 12 12 | 4 12 3 | 4 3
----------+----+-----+---------+-----------+------
. . x . . | 2 | 480 | 2 2 | 1 4 1 | 2 2
----------+----+-----+---------+-----------+------
. o3x . . | 3 | 3 | 320 * | 1 2 0 | 2 1
. . x3o . | 3 | 3 | * 320 | 0 2 1 | 1 2
----------+----+-----+---------+-----------+------
o3o3x . . ♦ 4 | 6 | 4 0 | 80 * * | 2 0
. o3x3o . ♦ 6 | 12 | 4 4 | * 160 * | 1 1
. . x3o4o ♦ 6 | 12 | 0 8 | * * 40 | 0 2
----------+----+-----+---------+-----------+------
o3o3x3o . ♦ 10 | 30 | 20 10 | 5 5 0 | 32 *
. o3x3o4o ♦ 24 | 96 | 32 64 | 0 16 8 | * 10
o3o3x3o4/3o
. . . . . | 80 ♦ 12 | 12 12 | 4 12 3 | 4 3
------------+----+-----+---------+-----------+------
. . x . . | 2 | 480 | 2 2 | 1 4 1 | 2 2
------------+----+-----+---------+-----------+------
. o3x . . | 3 | 3 | 320 * | 1 2 0 | 2 1
. . x3o . | 3 | 3 | * 320 | 0 2 1 | 1 2
------------+----+-----+---------+-----------+------
o3o3x . . ♦ 4 | 6 | 4 0 | 80 * * | 2 0
. o3x3o . ♦ 6 | 12 | 4 4 | * 160 * | 1 1
. . x3o4/3o ♦ 6 | 12 | 0 8 | * * 40 | 0 2
------------+----+-----+---------+-----------+------
o3o3x3o . ♦ 10 | 30 | 20 10 | 5 5 0 | 32 *
. o3x3o4/3o ♦ 24 | 96 | 32 64 | 0 16 8 | * 10
o3x3o *b3o3o
. . . . . | 80 ♦ 12 | 6 6 12 | 3 6 6 4 | 3 2 2
-------------+----+-----+-------------+-------------+---------
. x . . . | 2 | 480 | 1 1 2 | 1 2 2 1 | 2 1 1
-------------+----+-----+-------------+-------------+---------
o3x . . . | 3 | 3 | 160 * * | 1 2 0 0 | 2 1 0
. x3o . . | 3 | 3 | * 160 * | 1 0 2 0 | 2 0 1
. x . *b3o . | 3 | 3 | * * 320 | 0 1 1 1 | 1 1 1
-------------+----+-----+-------------+-------------+---------
o3x3o . . ♦ 6 | 12 | 4 4 0 | 40 * * * | 2 0 0
o3x . *b3o . ♦ 6 | 12 | 4 0 4 | * 80 * * | 1 1 0
. x3o *b3o . ♦ 6 | 12 | 0 4 4 | * * 80 * | 1 0 1
. x . *b3o3o ♦ 4 | 6 | 0 0 4 | * * * 80 | 0 1 1
-------------+----+-----+-------------+-------------+---------
o3x3o *b3o . ♦ 24 | 96 | 32 32 32 | 8 8 8 0 | 10 * *
o3x . *b3o3o ♦ 10 | 30 | 10 0 20 | 0 5 0 5 | * 16 *
. x3o *b3o3o ♦ 10 | 30 | 0 10 20 | 0 0 5 5 | * * 16
ooo3xox3oxo4ooo&#xt → both heights = 1/sqrt(2) = 0.707107
(ico || pseudo rit || ico)
o..3o..3o..4o.. & | 48 * ♦ 8 4 0 | 4 8 8 4 0 | 4 2 4 8 1 0 | 1 4 2
.o.3.o.3.o.4.o. | * 32 ♦ 0 6 6 | 0 0 6 12 6 | 0 0 2 12 3 2 | 0 4 3
----------------------+-------+------------+-------------------+--------------------+-------
... x.. ... ... & | 2 0 | 192 * * | 1 2 1 0 0 | 2 1 1 2 0 0 | 1 2 1
oo.3oo.3oo.4oo.&#x & | 1 1 | * 192 * | 0 0 2 2 0 | 0 0 1 4 1 0 | 0 2 2
... ... .x. ... | 0 2 | * * 96 | 0 0 0 2 2 | 0 0 0 4 1 1 | 0 2 2
----------------------+-------+------------+-------------------+--------------------+-------
o..3x.. ... ... & | 3 0 | 3 0 0 | 64 * * * * | 2 0 1 0 0 0 | 1 2 0
... x..3o.. ... & | 3 0 | 3 0 0 | * 128 * * * | 1 1 0 1 0 0 | 1 1 1
... xo. ... ...&#x & | 2 1 | 1 2 0 | * * 192 * * | 0 0 1 2 0 0 | 0 2 1
... ... ox. ...&#x & | 1 2 | 0 2 1 | * * * 192 * | 0 0 0 2 1 0 | 0 1 2
... .o.3.x. ... | 0 3 | 0 0 3 | * * * * 64 | 0 0 0 2 0 1 | 0 2 1
----------------------+-------+------------+-------------------+--------------------+-------
o..3x..3o.. ... & ♦ 6 0 | 12 0 0 | 4 4 0 0 0 | 32 * * * * * | 1 1 0
... x..3o..4o.. & ♦ 6 0 | 12 0 0 | 0 8 0 0 0 | * 16 * * * * | 1 0 1
oo.3xo. ... ...&#x & ♦ 3 1 | 3 3 0 | 1 0 3 0 0 | * * 64 * * * | 0 2 0
... xo.3ox. ...&#x & ♦ 3 3 | 3 6 3 | 0 1 3 3 1 | * * * 128 * * | 0 1 1
... ... oxo4ooo&#xt ♦ 2 4 | 0 8 4 | 0 0 0 8 0 | * * * * 24 * | 0 0 2
.o.3.o.3.x. ... ♦ 0 4 | 0 0 6 | 0 0 0 0 4 | * * * * * 16 | 0 2 0
----------------------+-------+------------+-------------------+--------------------+-------
o..3x..3o..4o.. & ♦ 24 0 | 96 0 0 | 32 64 0 0 0 | 16 8 0 0 0 0 | 2 * *
oo.3xo.3ox. ...&#x & ♦ 6 4 | 12 12 6 | 4 4 12 6 4 | 1 0 4 4 0 1 | * 32 *
... xox3oxo4ooo&#xt ♦ 12 12 | 24 48 24 | 0 16 24 48 8 | 0 2 0 16 6 0 | * * 8
oxo3xox3oxo *b3ooo&#xt → both heights = 1/sqrt(2) = 0.707107
(ico || pseudo rit || ico)
o..3o..3o.. *b3o.. & | 48 * ♦ 8 4 0 0 | 4 4 4 2 8 2 0 0 | 2 2 2 4 4 4 1 0 0 | 1 2 2 2
.o.3.o.3.o. *b3.o. | * 32 ♦ 0 6 3 3 | 0 0 0 6 6 6 3 3 | 0 0 0 6 6 2 3 1 1 | 0 2 2 3
-------------------------+-------+---------------+--------------------------+--------------------------+----------
... x.. ... ... & | 2 0 | 192 * * * | 1 1 1 0 1 0 0 0 | 1 1 1 1 1 1 0 0 0 | 1 1 1 1
oo.3oo.3oo. *b3oo.&#x & | 1 1 | * 192 * * | 0 0 0 1 2 1 0 0 | 0 0 0 2 2 1 1 0 0 | 0 1 1 2
.x. ... ... ... | 0 2 | * * 48 * | 0 0 0 2 0 0 2 0 | 0 0 0 4 0 0 1 1 0 | 0 2 0 2
... ... .x. ... | 0 2 | * * * 48 | 0 0 0 0 0 2 0 2 | 0 0 0 0 4 0 1 0 1 | 0 0 2 2
-------------------------+-------+---------------+--------------------------+--------------------------+----------
o..3x.. ... ... & | 3 0 | 3 0 0 0 | 64 * * * * * * * | 1 1 0 1 0 0 0 0 0 | 1 1 0 1
... x..3o.. ... & | 3 0 | 3 0 0 0 | * 64 * * * * * * | 1 0 1 0 1 0 0 0 0 | 1 0 1 1
... x.. ... *b3o.. & | 3 0 | 3 0 0 0 | * * 64 * * * * * | 0 1 1 0 0 1 0 0 0 | 1 1 1 0
ox. ... ... ...&#x & | 1 2 | 0 2 1 0 | * * * 96 * * * * | 0 0 0 2 0 0 1 0 0 | 0 1 0 2
... xo. ... ...&#x & | 2 1 | 1 2 0 0 | * * * * 192 * * * | 0 0 0 1 1 1 0 0 0 | 0 1 1 1
... ... ox. ...&#x & | 1 2 | 0 2 0 1 | * * * * * 96 * * | 0 0 0 0 2 0 1 0 0 | 0 0 1 2
.x.3.o. ... ... | 0 3 | 0 0 3 0 | * * * * * * 32 * | 0 0 0 2 0 0 0 1 0 | 0 2 0 1
... .o.3.x. ... | 0 3 | 0 0 0 3 | * * * * * * * 32 | 0 0 0 0 2 0 0 0 1 | 0 0 2 1
-------------------------+-------+---------------+--------------------------+--------------------------+----------
o..3x..3o.. ... & ♦ 6 0 | 12 0 0 0 | 4 4 0 0 0 0 0 0 | 16 * * * * * * * * | 1 0 0 1
o..3x.. ... *b3o.. & ♦ 6 0 | 12 0 0 0 | 4 0 4 0 0 0 0 0 | * 16 * * * * * * * | 1 1 0 0
... x..3o.. *b3o.. & ♦ 6 0 | 12 0 0 0 | 0 4 4 0 0 0 0 0 | * * 16 * * * * * * | 1 0 1 0
ox.3xo. ... ...&#x & ♦ 3 3 | 3 6 3 0 | 1 0 0 3 3 0 1 0 | * * * 64 * * * * * | 0 1 0 1
... xo.3ox. ...&#x & ♦ 3 3 | 3 6 0 3 | 0 1 0 0 3 3 0 1 | * * * * 64 * * * * | 0 0 1 1
... xo. ... *b3oo.&#x & ♦ 3 1 | 3 3 0 0 | 0 0 1 0 3 0 0 0 | * * * * * 64 * * * | 0 1 1 0
oxo ... oxo ...&#xt ♦ 2 4 | 0 8 2 2 | 0 0 0 4 0 4 0 0 | * * * * * * 24 * * | 0 0 0 2
.x.3.o. ... *b3.o. ♦ 0 4 | 0 0 6 0 | 0 0 0 0 0 0 4 0 | * * * * * * * 8 * | 0 2 0 0
... .o.3.x. *b3.o. ♦ 0 4 | 0 0 0 6 | 0 0 0 0 0 0 0 4 | * * * * * * * * 8 | 0 0 2 0
-------------------------+-------+---------------+--------------------------+--------------------------+----------
o..3x..3o.. *b3o.. & ♦ 24 0 | 96 0 0 0 | 32 32 32 0 0 0 0 0 | 8 8 8 0 0 0 0 0 0 | 2 * * *
ox.3xo. ... *b3oo.&#x & ♦ 6 4 | 12 12 6 0 | 4 0 4 6 12 0 4 0 | 0 1 0 4 0 4 0 1 0 | * 16 * *
... xo.3ox. *b3oo.&#x & ♦ 6 4 | 12 12 0 6 | 0 4 4 0 12 6 0 4 | 0 0 1 0 4 4 0 0 1 | * * 16 *
oxo3xox3oxo ... ♦ 12 12 | 24 48 12 12 | 8 8 0 24 24 24 4 4 | 2 0 0 8 8 0 6 0 0 | * * * 8
oxoo3xoxo3oxox3ooxo&#xt → all heights = sqrt(2/5) = 0.632456
(rap || pseudo srip || pseudo inv srip || inv rap)
o...3o...3o...3o... & | 20 * ♦ 6 6 0 0 0 | 3 6 3 6 6 0 0 0 0 0 | 3 2 3 6 2 3 0 0 0 0 | 1 2 3 1
.o..3.o..3.o..3.o.. & | * 60 ♦ 0 2 2 4 4 | 0 0 2 1 4 1 2 2 6 6 | 0 0 1 2 2 5 1 4 2 2 | 0 1 3 3
--------------------------+-------+-------------------+----------------------------------+-------------------------------+-----------
.... x... .... .... & | 2 0 | 60 * * * * | 1 2 0 1 0 0 0 0 0 0 | 2 1 1 2 0 0 0 0 0 0 | 1 1 2 0
oo..3oo..3oo..3oo..&#x & | 1 1 | * 120 * * * | 0 0 1 1 2 0 0 0 0 0 | 0 0 1 2 1 2 0 0 0 0 | 0 1 2 1
.x.. .... .... .... & | 0 2 | * * 60 * * | 0 0 1 0 0 1 0 0 2 0 | 0 0 1 0 0 2 0 2 1 0 | 0 0 2 2
.... .... .x.. .... & | 0 2 | * * * 120 * | 0 0 0 0 1 0 1 1 0 1 | 0 0 0 1 1 1 1 1 0 1 | 0 1 2 1
.oo.3.oo.3.oo.3.oo.&#x | 0 2 | * * * * 120 | 0 0 0 0 0 0 0 0 2 2 | 0 0 0 0 0 2 0 2 1 1 | 0 0 2 2
--------------------------+-------+-------------------+----------------------------------+-------------------------------+-----------
o...3x... .... .... & | 3 0 | 3 0 0 0 0 | 20 * * * * * * * * * | 2 0 1 0 0 0 0 0 0 0 | 1 0 2 0
.... x...3o... .... & | 3 0 | 3 0 0 0 0 | * 40 * * * * * * * * | 1 1 0 1 0 0 0 0 0 0 | 1 1 1 0
ox.. .... .... ....&#x & | 1 2 | 0 2 1 0 0 | * * 60 * * * * * * * | 0 0 1 0 0 2 0 0 0 0 | 0 0 2 1
.... xo.. .... ....&#x & | 2 1 | 1 2 0 0 0 | * * * 60 * * * * * * | 0 0 1 2 0 0 0 0 0 0 | 0 1 2 0
.... .... ox.. ....&#x & | 1 2 | 0 2 0 1 0 | * * * * 120 * * * * * | 0 0 0 1 1 1 0 0 0 0 | 0 1 1 1
.x..3.o.. .... .... & | 0 3 | 0 0 3 0 0 | * * * * * 20 * * * * | 0 0 1 0 0 0 0 2 0 0 | 0 0 2 1
.... .o..3.x.. .... & | 0 3 | 0 0 0 3 0 | * * * * * * 40 * * * | 0 0 0 1 0 0 1 0 0 1 | 0 1 2 0
.... .... .x..3.o.. & | 0 3 | 0 0 0 3 0 | * * * * * * * 40 * * | 0 0 0 0 1 0 1 1 0 0 | 0 1 1 1
.xo. .... .... ....&#x & | 0 3 | 0 0 1 0 2 | * * * * * * * * 120 * | 0 0 0 0 0 1 0 1 1 0 | 0 0 1 2
.... .ox. .... ....&#x & | 0 3 | 0 0 0 1 2 | * * * * * * * * * 120 | 0 0 0 0 0 1 0 1 0 1 | 0 0 2 1
--------------------------+-------+-------------------+----------------------------------+-------------------------------+-----------
o...3x...3o... .... & ♦ 6 0 | 12 0 0 0 0 | 4 4 0 0 0 0 0 0 0 0 | 10 * * * * * * * * * | 1 0 1 0
.... x...3o...3o... & ♦ 4 0 | 6 0 0 0 0 | 0 4 0 0 0 0 0 0 0 0 | * 10 * * * * * * * * | 1 1 0 0
ox..3xo.. .... ....&#x & ♦ 3 3 | 3 6 3 0 0 | 1 0 3 3 0 1 0 0 0 0 | * * 20 * * * * * * * | 0 0 2 0
.... xo..3ox.. ....&#x & ♦ 3 3 | 3 6 0 3 0 | 0 1 0 3 3 0 1 0 0 0 | * * * 40 * * * * * * | 0 1 1 0
.... .... ox..3oo..&#x & ♦ 1 3 | 0 3 0 3 0 | 0 0 0 0 3 0 0 1 0 0 | * * * * 40 * * * * * | 0 1 0 1
oxo. .... oxo. ....&#xt & ♦ 1 5 | 0 4 2 2 4 | 0 0 2 0 2 0 0 0 2 2 | * * * * * 60 * * * * | 0 0 1 1
.... .o..3.x..3.o.. & ♦ 0 6 | 0 0 0 12 0 | 0 0 0 0 0 0 4 4 0 0 | * * * * * * 10 * * * | 0 1 1 0
.xo.3.ox. .... ....&#x & ♦ 0 6 | 0 0 3 3 6 | 0 0 0 0 0 1 0 1 3 3 | * * * * * * * 40 * * | 0 0 1 1
.xo. .... .... .ox.&#x ♦ 0 4 | 0 0 2 0 4 | 0 0 0 0 0 0 0 0 4 0 | * * * * * * * * 30 * | 0 0 0 2
.... .ox.3.xo. ....&#x ♦ 0 6 | 0 0 0 6 6 | 0 0 0 0 0 0 2 0 0 6 | * * * * * * * * * 20 | 0 0 2 0
--------------------------+-------+-------------------+----------------------------------+-------------------------------+-----------
o...3x...3o...3o... & ♦ 10 0 | 30 0 0 0 0 | 10 20 0 0 0 0 0 0 0 0 | 5 5 0 0 0 0 0 0 0 0 | 2 * * *
.... xo..3ox..3oo..&#x & ♦ 4 6 | 6 12 0 12 0 | 0 4 0 6 12 0 4 4 0 0 | 0 1 0 4 4 0 1 0 0 0 | * 10 * *
oxo.3xox.3oxo. ....&#xt & ♦ 6 18 | 12 24 12 24 24 | 4 4 12 12 12 4 8 4 12 24 | 1 0 4 4 0 6 1 4 0 4 | * * 10 *
oxo. .... oxo.3oox.&#xt & ♦ 1 9 | 0 6 6 6 12 | 0 0 3 0 6 1 0 2 12 6 | 0 0 0 0 2 3 0 2 3 0 | * * * 20
ox(uoo)xo3xo(oxo)ox3ox(oou)xo ox(ouo)xo&#xt → all non-zero heights = height = 1/2
(oct || pseudo cope || pseudo compound of u-tet + u-laced ope + dual u-tet || pseudo cope || inv oct)
o.(...)..3o.(...)..3o.(...).. o.(...).. & | 12 * * * ♦ 4 8 0 0 0 0 0 0 | 4 8 8 4 0 0 0 0 0 0 0 0 | 1 8 2 4 4 0 0 0 0 0 0 | 2 4 1 0
.o(...)..3.o(...)..3.o(...).. .o(...).. & | * 48 * * ♦ 0 2 4 1 2 2 1 0 | 0 4 1 2 2 4 2 4 1 2 2 0 | 0 2 2 4 1 2 2 4 1 1 0 | 1 2 2 2
..(o..)..3..(o..)..3..(o..).. ..(o..).. & | * * 8 * ♦ 0 0 0 0 12 0 0 0 | 0 0 0 0 0 12 6 0 0 6 0 0 | 0 0 0 6 0 4 0 6 3 0 0 | 0 2 3 2
..(.o.)..3..(.o.)..3..(.o.).. ..(.o.).. | * * * 12 ♦ 0 0 0 0 0 8 0 4 | 0 0 0 0 0 0 0 8 8 0 4 4 | 0 0 2 0 0 0 8 4 0 4 1 | 2 0 1 4
----------------------------------------------+------------+-------------------------+-------------------------------------+--------------------------------+----------
..(...).. x.(...).. ..(...).. ..(...).. & | 2 0 0 0 | 24 * * * * * * * | 2 0 2 0 0 0 0 0 0 0 0 0 | 1 4 0 0 1 0 0 0 0 0 0 | 2 2 0 0
oo(...)..3oo(...)..3oo(...).. oo(...)..&#x & | 1 1 0 0 | * 96 * * * * * * | 0 2 1 1 0 0 0 0 0 0 0 0 | 0 2 1 2 1 0 0 0 0 0 0 | 1 2 1 0
.x(...).. ..(...).. ..(...).. ..(...).. & | 0 2 0 0 | * * 96 * * * * * | 0 1 0 0 1 1 0 1 0 0 0 0 | 0 1 1 1 0 1 1 1 0 0 0 | 1 1 1 1
..(...).. ..(...).. ..(...).. .x(...).. & | 0 2 0 0 | * * * 24 * * * * | 0 0 0 2 0 0 2 0 0 0 0 0 | 0 0 0 4 1 0 0 0 1 0 0 | 0 2 2 0
.o(o..)..3.o(o..)..3.o(o..).. .o(o..)..&#x & | 0 1 1 0 | * * * * 96 * * * | 0 0 0 0 0 2 1 0 0 1 0 0 | 0 0 0 2 0 1 0 2 1 0 0 | 0 1 2 1
.o(.o.)..3.o(.o.)..3.o(.o.).. .o(.o.)..&#x & | 0 1 0 1 | * * * * * 96 * * | 0 0 0 0 0 0 0 2 1 0 1 0 | 0 0 1 0 0 0 2 2 0 1 0 | 1 0 1 2
.o(...)o.3.o(...)o.3.o(...)o. .o(...)o.&#x | 0 2 0 0 | * * * * * * 24 * | 0 0 0 0 0 0 0 0 0 2 2 0 | 0 0 0 0 0 0 0 4 1 1 0 | 0 0 2 2
..(...).. ..(.x.).. ..(...).. ..(...).. | 0 0 0 2 | * * * * * * * 24 | 0 0 0 0 0 0 0 0 2 0 0 2 | 0 0 0 0 0 0 4 0 0 1 1 | 2 0 0 2
----------------------------------------------+------------+-------------------------+-------------------------------------+--------------------------------+----------
o.(...)..3x.(...).. ..(...).. ..(...).. & | 3 0 0 0 | 3 0 0 0 0 0 0 0 | 16 * * * * * * * * * * * | 1 2 0 0 0 0 0 0 0 0 0 | 2 1 0 0
ox(...).. ..(...).. ..(...).. ..(...)..&#x & | 1 2 0 0 | 0 2 1 0 0 0 0 0 | * 96 * * * * * * * * * * | 0 1 1 1 0 0 0 0 0 0 0 | 1 1 1 0
..(...).. xo(...).. ..(...).. ..(...)..&#x & | 2 1 0 0 | 1 2 0 0 0 0 0 0 | * * 48 * * * * * * * * * | 0 2 0 0 1 0 0 0 0 0 0 | 1 2 0 0
..(...).. ..(...).. ..(...).. ox(...)..&#x & | 1 2 0 0 | 0 2 0 1 0 0 0 0 | * * * 48 * * * * * * * * | 0 0 0 2 1 0 0 0 0 0 0 | 0 2 1 0
.x(...)..3.o(...).. ..(...).. ..(...).. & | 0 3 0 0 | 0 0 3 0 0 0 0 0 | * * * * 32 * * * * * * * | 0 1 0 0 0 1 1 0 0 0 0 | 1 1 0 1
..(...).. ..(...).. .x(o..).. ..(...)..&#x & | 0 2 1 0 | 0 0 1 0 2 0 0 0 | * * * * * 96 * * * * * * | 0 0 0 1 0 1 0 1 0 0 0 | 1 1 0 1
..(...).. ..(...).. ..(...).. .x(o..)..&#x & | 0 2 1 0 | 0 0 0 1 2 0 0 0 | * * * * * * 48 * * * * * | 0 0 0 2 0 0 0 0 1 0 0 | 0 1 2 0
.x(.o.).. ..(...).. ..(...).. ..(...)..&#x & | 0 2 0 1 | 0 0 1 0 0 2 0 0 | * * * * * * * 96 * * * * | 0 0 1 0 0 0 1 1 0 0 0 | 1 0 1 1
..(...).. .o(.x.).. ..(...).. ..(...)..&#x & | 0 1 0 2 | 0 0 0 0 0 2 0 1 | * * * * * * * * 48 * * * | 0 0 0 0 0 0 2 0 0 1 0 | 1 0 0 2
.o(o..)o.3.o(o..)o.3.o(o..)o. .o(o..)o.&#x & | 0 2 1 0 | 0 0 0 0 2 0 1 0 | * * * * * * * * * 48 * * | 0 0 0 0 0 0 0 2 1 0 0 | 0 0 2 1
.o(.o.)o.3.o(.o.)o.3.o(.o.)o. .o(.o.)o.&#x | 0 2 0 1 | 0 0 0 0 0 2 1 0 | * * * * * * * * * * 48 * | 0 0 0 0 0 0 0 2 0 1 0 | 0 0 1 2
..(.o.)..3..(.x.).. ..(...).. ..(...).. & | 0 0 0 3 | 0 0 0 0 0 0 0 3 | * * * * * * * * * * * 16 | 0 0 0 0 0 0 2 0 0 0 1 | 2 0 0 1
----------------------------------------------+------------+-------------------------+-------------------------------------+--------------------------------+----------
o.(...)..3x.(...)..3o.(...).. ..(...).. & ♦ 6 0 0 0 | 12 0 0 0 0 0 0 0 | 8 0 0 0 0 0 0 0 0 0 0 0 | 2 * * * * * * * * * * | 2 0 0 0
ox(...)..3xo(...).. ..(...).. ..(...)..&#x & ♦ 3 3 0 0 | 3 6 3 0 0 0 0 0 | 1 3 3 0 1 0 0 0 0 0 0 0 | * 32 * * * * * * * * * | 1 1 0 0
ox(.o.).. ..(...).. ox(.o.).. ..(...)..&#xt & ♦ 1 4 0 1 | 0 4 4 0 0 4 0 0 | 0 4 0 0 0 0 0 4 0 0 0 0 | * * 24 * * * * * * * * | 1 0 1 0
ox(..o).. ..(...).. ..(...).. ox(..o)..&#xt & ♦ 1 4 1 0 | 0 4 2 2 4 0 0 0 | 0 2 0 2 0 2 2 0 0 0 0 0 | * * * 48 * * * * * * * | 0 1 1 0
..(...).. xo(...).. ..(...).. ox(...)..&#x & ♦ 2 2 0 0 | 1 4 0 1 0 0 0 0 | 0 0 2 2 0 0 0 0 0 0 0 0 | * * * * 24 * * * * * * | 0 2 0 0
..(...).. .o(o..)..3.x(o..).. ..(...)..&#x & ♦ 0 3 1 0 | 0 0 3 0 3 0 0 0 | 0 0 0 0 1 3 0 0 0 0 0 0 | * * * * * 32 * * * * * | 0 1 0 1
.x(.o.)..3.o(.x.).. ..(...).. ..(...)..&#x & ♦ 0 3 0 3 | 0 0 3 0 0 6 0 3 | 0 0 0 0 1 0 0 3 3 0 0 1 | * * * * * * 32 * * * * | 1 0 0 1
..(...).. ..(...).. .x(oo.)x. ..(...)..&#xr & ♦ 0 4 1 1 | 0 0 2 0 4 4 2 0 | 0 0 0 0 0 2 0 2 0 2 2 0 | * * * * * * * 48 * * * | 0 0 1 1
..(...).. ..(...).. ..(...).. .x(o.o)x.&#xr & ♦ 0 4 2 0 | 0 0 0 2 8 0 2 0 | 0 0 0 0 0 0 4 0 0 4 0 0 | * * * * * * * * 12 * * | 0 0 2 0
..(...).. .o(.x.)o. ..(...).. ..(...)..&#x ♦ 0 2 0 2 | 0 0 0 0 0 4 1 1 | 0 0 0 0 0 0 0 0 2 0 2 0 | * * * * * * * * * 24 * | 0 0 0 2
..(.o.)..3..(.x.)..3..(.o.).. ..(...).. ♦ 0 0 0 6 | 0 0 0 0 0 0 0 12 | 0 0 0 0 0 0 0 0 0 0 0 8 | * * * * * * * * * * 2 | 2 0 0 0
----------------------------------------------+------------+-------------------------+-------------------------------------+--------------------------------+----------
ox(.o.)..3xo(.x.)..3ox(.o.).. ..(...)..&#xt & ♦ 6 12 0 6 | 12 24 24 0 0 24 0 12 | 8 24 12 0 8 0 0 24 12 0 0 8 | 1 8 6 0 0 0 8 0 0 0 1 | 4 * * *
ox(..o)..3xo(..o).. ..(...).. ox(..o)..&#xt & ♦ 3 6 1 0 | 3 12 6 3 6 0 0 0 | 1 6 6 6 2 6 3 0 0 0 0 0 | 0 2 0 3 3 2 0 0 0 0 0 | * 16 * *
ox(uoo)xo ..(...).. ox(oou)xo ox(ouo)xo&#xt ♦ 2 16 4 2 | 0 16 16 8 32 16 8 0 | 0 16 0 8 0 16 16 16 0 16 8 0 | 0 0 4 8 0 0 0 8 4 0 0 | * * 6 *
.x(.oo)x.3.o(.xo)o. ..(...).. ..(...)..&#xr & ♦ 0 6 1 3 | 0 0 6 0 6 12 3 3 | 0 0 0 0 2 6 0 6 6 3 6 1 | 0 0 0 0 0 2 2 3 0 3 0 | * * * 16
oox3oxo4qoo oxo4ooq&#zx → heights = 0
(tegum sum of q-cube, squaco, and gyro (q,x)-squoct)
seen in the above lace hyper city as central 4-layered line-tower, rhombical oriented 3-layered x-square tower, and dualy-oriented 2-layered q-square tower respectively, from front to back
o..3o..4o.. o..4o.. | 8 * * ♦ 12 0 0 0 0 | 12 12 0 0 0 0 0 | 4 3 12 0 0 0 0 | 4 3 0
.o.3.o.4.o. .o.4.o. | * 48 * ♦ 2 4 2 4 0 | 4 4 2 2 8 4 0 | 2 1 8 4 2 2 0 | 4 2 1
..o3..o4..o ..o4..o | * * 24 ♦ 0 0 0 8 4 | 0 0 0 8 8 4 4 | 0 0 4 8 4 2 1 | 4 1 2
------------------------+---------+-----------------+-----------------------+---------------------+-------
oo.3oo.4oo. oo.4oo.&#x | 1 1 0 | 96 * * * * | 2 2 0 0 0 0 0 | 1 1 4 0 0 0 0 | 2 2 0
... .x. ... ... ... | 0 2 0 | * 96 * * * | 1 0 1 0 2 0 0 | 1 0 2 2 0 1 0 | 2 1 1
... ... ... .x. ... | 0 2 0 | * * 48 * * | 0 2 0 0 0 2 0 | 0 1 4 0 1 0 0 | 2 2 0
.oo3.oo4.oo .oo4.oo&#x | 0 1 1 | * * * 192 * | 0 0 0 1 2 1 0 | 0 0 2 2 1 1 0 | 2 1 1
..x ... ... ... ... | 0 0 2 | * * * * 48 | 0 0 0 2 0 0 2 | 0 0 0 4 1 0 1 | 2 0 2
------------------------+---------+-----------------+-----------------------+---------------------+-------
... ox. ... ... ...&#x | 1 2 0 | 2 1 0 0 0 | 96 * * * * * * | 1 0 2 0 0 0 0 | 2 1 0
... ... ... ox. ...&#x | 1 2 0 | 2 0 1 0 0 | * 96 * * * * * | 0 1 2 0 0 0 0 | 1 2 0
.o.3.x. ... ... ... | 0 3 0 | 0 3 0 0 0 | * * 32 * * * * | 1 0 0 2 0 0 0 | 2 0 1
.ox ... ... ... ...&#x | 0 1 2 | 0 0 0 2 1 | * * * 96 * * * | 0 0 0 2 1 0 0 | 2 0 1
... .xo ... ... ...&#x | 0 2 1 | 0 1 0 2 0 | * * * * 192 * * | 0 0 1 1 0 1 0 | 1 1 1
... ... ... .xo ...&#x | 0 2 1 | 0 0 1 2 0 | * * * * * 96 * | 0 0 2 0 1 0 0 | 2 1 0
..x3..o ... ... ... | 0 0 3 | 0 0 0 0 3 | * * * * * * 32 | 0 0 0 2 0 0 1 | 1 0 2
------------------------+---------+-----------------+-----------------------+---------------------+-------
oo.3ox. ... ... ...&#x ♦ 1 3 0 | 3 3 0 0 0 | 3 0 1 0 0 0 0 | 32 * * * * * * | 2 0 0
... ... qo. ox.4oo.&#zx ♦ 2 4 0 | 8 0 4 0 0 | 0 8 0 0 0 0 0 | * 12 * * * * * | 0 2 0
... oxo ... oxo ...&#xt ♦ 1 4 1 | 4 2 2 4 0 | 2 2 0 0 2 2 0 | * * 96 * * * * | 1 1 0
.ox3.xo ... ... ...&#x ♦ 0 3 3 | 0 3 0 6 3 | 0 0 1 3 3 0 1 | * * * 64 * * * | 1 0 1
.ox ... ... .xo ...&#x ♦ 0 2 2 | 0 0 1 4 1 | 0 0 0 2 0 2 0 | * * * * 48 * * | 2 0 0
... .xo4.oo ... .oq&#zx ♦ 0 4 2 | 0 4 0 8 0 | 0 0 0 0 8 0 0 | * * * * * 24 * | 0 1 1
..x3..o4..o ... ... ♦ 0 0 6 | 0 0 0 0 12 | 0 0 0 0 0 0 8 | * * * * * * 4 | 0 0 2
------------------------+---------+-----------------+-----------------------+---------------------+-------
oox3oxo ... oxo ...&#x ♦ 1 6 3 | 6 6 3 12 3 | 6 3 2 6 6 6 1 | 2 0 3 2 3 0 0 | 32 * *
... oxo4qoo oxo4ooq&#zx ♦ 4 16 4 | 32 16 16 32 0 | 16 32 0 0 32 16 0 | 0 4 16 0 0 4 0 | * 6 *
.ox3.xo4.oo ... .oq&#zx ♦ 0 12 12 | 0 24 0 48 24 | 0 0 8 24 48 0 16 | 0 0 0 16 0 6 2 | * * 4
ox(ou)x(xo)oo3oo(xo)x(ou)xo ox(oo)x(oo)xo4oo(qo)o(qo)oo&#xt → all heights = 1/sqrt(6) = 0.408248
(pt || pseudo tisdip || pseudo compound of bidual (x,q)-tisdip and u-{3} || pseudo shiddip || pseudo compound of para-dual (x,q)-tisdip and dual u-{3} || pseudo dual-para tisdip || pt)
...