Acronym	spid
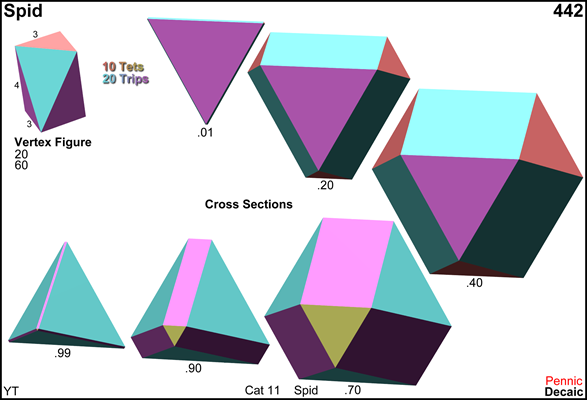
Name	small prismatodecachoron, runcinated pentachoron, expanded pentachoron, pyroperichoron, tetaco gyrobicupola, vertex figure of cypit, lattice A4 contact polytope (span of its roots), equatorial cross-section of pen-first scad, equatorial cross-section of rap-first rat
	©
Cross sections	©
Circumradius	1
Inradius wrt. tet	sqrt(5/8) = 0.790569
Inradius wrt. trip	sqrt(5/12) = 0.645497
Vertex figure	©
Vertex layers	Layer Symmetry Subsymmetries   o3o3o3o o3o3o . o3o . o o . o3o . o3o3o 1 x3o3o3x x3o3o . tet first x3o . x trip first x . o3x trip first . o3o3x tet first 2a x3o3x . x3x . o o . x3x . x3o3x 2b o3o . u u . o3o 3 o3o3x . opposite tet o3x . x opposite trip x . x3o opposite trip . x3o3o opposite tet
Lace city in approx. ASCII-art	_+------------ x x3o (trip) _/ _+------- compound of u o3o and o x3x _/ _/ _+-- x o3x (inv trip) x3o o3o -- x3o3o (tet) x3o x3x o3x -- x3o3x (co) o3o o3x -- o3o3x (dual tet)
	x o o x -- x3o3o (tet) 1 2 x x uo ou x x -- x3o3x (co) 6 78 3 o x x o -- o3o3x (dual tet) 5 4
	© o o + - o - # + o + - o o where: o = equatorial vertices +,- = perpendicular edges above/below # = 2 equatorial vertices at double-length perpendicular distance
Lace hyper city in approx. ASCII-art	x x x x x3o (trip) o o o u o o o compound of u o3o and o x3x x x x x o3x (inv trip)
Volume	35 sqrt(5)/48 = 1.630466
Surface	5 sqrt(2)/6+5 sqrt(3) = 9.838765
General of army	(is itself convex)
Colonel of regiment	(is itself locally convex – other uniform polychoral members: by cells: cho co oho tet trip nipdip 5 0 0 5 10 piphid 0 5 0 5 10 duhd 0 0 5 10 0 phud 0 0 5 0 20 spid 0 0 0 10 20 )
Dihedral angles	at {4} between trip and trip:   arccos(-2/3) = 131.810315° at {3} between tet and trip:   arccos(-sqrt(3/8)) = 127.761244°
Dual	m3o3o3m
Face vector	20, 60, 70, 30
Confer	more general: xPo3o...o3oPxQ*a   compounds: dopix   related segmentochora: tet || co   tet || tricu   {6} || trip   related CRFs: gyspid   decompositions: spidpy   ambification: respid   general polytopal classes: Wythoffian polychora   bistratic lace towers   lace simplices   analogs: maximal epanded simplex eSn
External links

Note that spid can be thought of as the external blend of 10 pens + 20 trippies. This decomposition is described as the degenerate segmentoteron ox3oo3oo3ox&#x.

By virtue of an outer symmetry this is a non-quasiregular monotoxal polychoron, that is all edges belong to the same equivalence class.

Incidence matrix according to Dynkin symbol

x3o3o3x

. . . . | 20 ♦  3  3 |  3  6  3 | 1  3  3 1
--------+----+-------+----------+----------
x . . . |  2 | 30  * |  2  2  0 | 1  2  1 0
. . . x |  2 |  * 30 |  0  2  2 | 0  1  2 1
--------+----+-------+----------+----------
x3o . . |  3 |  3  0 | 20  *  * | 1  1  0 0
x . . x |  4 |  2  2 |  * 30  * | 0  1  1 0
. . o3x |  3 |  0  3 |  *  * 20 | 0  0  1 1
--------+----+-------+----------+----------
x3o3o . ♦  4 |  6  0 |  4  0  0 | 5  *  * *
x3o . x ♦  6 |  6  3 |  2  3  0 | * 10  * *
x . o3x ♦  6 |  3  6 |  0  3  2 | *  * 10 *
. o3o3x ♦  4 |  0  6 |  0  0  4 | *  *  * 5

or
. . . .    | 20 ♦  6 |  6  6 |  2  6
-----------+----+----+-------+------
x . . .  & |  2 | 60 |  2  2 |  1  3
-----------+----+----+-------+------
x3o . .  & |  3 |  3 | 40  * |  1  1
x . . x    |  4 |  4 |  * 30 |  0  2
-----------+----+----+-------+------
x3o3o .  & ♦  4 |  6 |  4  0 | 10  *
x3o . x  & ♦  6 |  9 |  2  3 |  * 20

snubbed forms: β3o3o3x, β3o3o3β

x3o3/2o3/2x

. .   .   . | 20 ♦  3  3 |  3  6  3 | 1  3  3 1
------------+----+-------+----------+----------
x .   .   . |  2 | 30  * |  2  2  0 | 1  2  1 0
. .   .   x |  2 |  * 30 |  0  2  2 | 0  1  2 1
------------+----+-------+----------+----------
x3o   .   . |  3 |  3  0 | 20  *  * | 1  1  0 0
x .   .   x |  4 |  2  2 |  * 30  * | 0  1  1 0
. .   o3/2x |  3 |  0  3 |  *  * 20 | 0  0  1 1
------------+----+-------+----------+----------
x3o3/2o   . ♦  4 |  6  0 |  4  0  0 | 5  *  * *
x3o   .   x ♦  6 |  6  3 |  2  3  0 | * 10  * *
x .   o3/2x ♦  6 |  3  6 |  0  3  2 | *  * 10 *
. o3/2o3/2x ♦  4 |  0  6 |  0  0  4 | *  *  * 5

x3/2o3o3/2x

.   . .   . | 20 ♦  3  3 |  3  6  3 | 1  3  3 1
------------+----+-------+----------+----------
x   . .   . |  2 | 30  * |  2  2  0 | 1  2  1 0
.   . .   x |  2 |  * 30 |  0  2  2 | 0  1  2 1
------------+----+-------+----------+----------
x3/2o .   . |  3 |  3  0 | 20  *  * | 1  1  0 0
x   . .   x |  4 |  2  2 |  * 30  * | 0  1  1 0
.   . o3/2x |  3 |  0  3 |  *  * 20 | 0  0  1 1
------------+----+-------+----------+----------
x3/2o3o   . ♦  4 |  6  0 |  4  0  0 | 5  *  * *
x3/2o .   x ♦  6 |  6  3 |  2  3  0 | * 10  * *
x   . o3/2x ♦  6 |  3  6 |  0  3  2 | *  * 10 *
.   o3o3/2x ♦  4 |  0  6 |  0  0  4 | *  *  * 5

xxo3ooo3oxx&#xt   → both heights = sqrt(5/8) = 0.790569
(tet || pseudo co || dual tet)

o..3o..3o..    | 4  * * ♦ 3  3  0  0  0 0 | 3  6  3 0 0 0  0  0 0 | 1 3 3 1 0 0 0 0
.o.3.o.3.o.    | * 12 * ♦ 0  1  2  2  1 0 | 0  2  2 1 2 1  2  2 0 | 0 1 2 1 1 2 1 0
..o3..o3..o    | *  * 4 ♦ 0  0  0  0  3 3 | 0  0  0 0 0 0  3  6 3 | 0 0 0 0 1 3 3 1
---------------+--------+-----------------+-----------------------+----------------
x.. ... ...    | 2  0 0 | 6  *  *  *  * * | 2  2  0 0 0 0  0  0 0 | 1 2 1 0 0 0 0 0
oo.3oo.3oo.&#x | 1  1 0 | * 12  *  *  * * | 0  2  2 0 0 0  0  0 0 | 0 1 2 1 0 0 0 0
.x. ... ...    | 0  2 0 | *  * 12  *  * * | 0  1  0 1 1 0  1  0 0 | 0 1 1 0 1 1 0 0
... ... .x.    | 0  2 0 | *  *  * 12  * * | 0  0  1 0 1 1  0  1 0 | 0 0 1 1 0 1 1 0
.oo3.oo3.oo&#x | 0  1 1 | *  *  *  * 12 * | 0  0  0 0 0 0  2  2 0 | 0 0 0 0 1 1 1 0
... ... ..x    | 0  0 2 | *  *  *  *  * 6 | 0  0  0 0 0 0  0  2 2 | 0 0 0 0 0 1 2 1
---------------+--------+-----------------+-----------------------+----------------
x..3o.. ...    | 3  0 0 | 3  0  0  0  0 0 | 4  *  * * * *  *  * * | 1 1 0 0 0 0 0 0
xx. ... ...&#x | 2  2 0 | 1  2  1  0  0 0 | * 12  * * * *  *  * * | 0 1 1 0 0 0 0 0
... ... ox.&#x | 1  2 0 | 0  2  0  1  0 0 | *  * 12 * * *  *  * * | 0 0 1 1 0 0 0 0
.x.3.o. ...    | 0  3 0 | 0  0  3  0  0 0 | *  *  * 4 * *  *  * * | 0 1 0 0 1 0 0 0
.x. ... .x.    | 0  4 0 | 0  0  2  2  0 0 | *  *  * * 6 *  *  * * | 0 0 1 0 0 1 0 0
... .o.3.x.    | 0  3 0 | 0  0  0  3  0 0 | *  *  * * * 4  *  * * | 0 0 0 1 0 0 1 0
.xo ... ...&#x | 0  2 1 | 0  0  1  0  2 0 | *  *  * * * * 12  * * | 0 0 0 0 1 1 0 0
... ... .xx&#x | 0  2 2 | 0  0  0  1  2 1 | *  *  * * * *  * 12 * | 0 0 0 0 0 1 1 0
... ..o3..x    | 0  0 3 | 0  0  0  0  0 3 | *  *  * * * *  *  * 4 | 0 0 0 0 0 0 1 1
---------------+--------+-----------------+-----------------------+----------------
x..3o..3o..    ♦ 4  0 0 | 6  0  0  0  0 0 | 4  0  0 0 0 0  0  0 0 | 1 * * * * * * *
xx.3oo. ...&#x ♦ 3  3 0 | 3  3  3  0  0 0 | 1  3  0 1 0 0  0  0 0 | * 4 * * * * * *
xx. ... ox.&#x ♦ 2  4 0 | 1  4  2  2  0 0 | 0  2  2 0 1 0  0  0 0 | * * 6 * * * * *
... oo.3ox.&#x ♦ 1  3 0 | 0  3  0  3  0 0 | 0  0  3 0 0 1  0  0 0 | * * * 4 * * * *
.xo3.oo ...&#x ♦ 0  3 1 | 0  0  3  0  3 0 | 0  0  0 1 0 0  3  0 0 | * * * * 4 * * *
.xo ... .xx&#x ♦ 0  4 2 | 0  0  2  2  4 1 | 0  0  0 0 1 0  2  2 0 | * * * * * 6 * *
... .oo3.xx&#x ♦ 0  3 3 | 0  0  0  3  3 3 | 0  0  0 0 0 1  0  3 1 | * * * * * * 4 *
..o3..o3..x    ♦ 0  0 4 | 0  0  0  0  0 6 | 0  0  0 0 0 0  0  0 4 | * * * * * * * 1

or
o..3o..3o..    & | 8  * ♦  3  3  0 | 3  6  3 0 0 | 1 3  3 1
.o.3.o.3.o.      | * 12 ♦  0  2  4 | 0  4  4 2 2 | 0 2  2 1
-----------------+------+----------+-------------+---------
x.. ... ...    & | 2  0 | 12  *  * | 2  2  0 0 0 | 1 2  1 0
oo.3oo.3oo.&#x & | 1  1 |  * 24  * | 0  2  2 0 0 | 0 1  2 1
.x. ... ...    & | 0  2 |  *  * 24 | 0  1  1 1 1 | 0 1  2 1
-----------------+------+----------+-------------+---------
x..3o.. ...    & | 3  0 |  3  0  0 | 8  *  * * * | 1 1  0 0
xx. ... ...&#x & | 2  2 |  1  2  1 | * 24  * * * | 0 1  1 0
... ... ox.&#x & | 1  2 |  0  2  1 | *  * 24 * * | 0 0  1 1
.x.3.o. ...    & | 0  3 |  0  0  3 | *  *  * 8 * | 0 1  0 1
.x. ... .x.      | 0  4 |  0  0  4 | *  *  * * 6 | 0 0  2 0
-----------------+------+----------+-------------+---------
x..3o..3o..    & ♦ 4  0 |  6  0  0 | 4  0  0 0 0 | 2 *  * *
xx.3oo. ...&#x & ♦ 3  3 |  3  3  3 | 1  3  0 1 0 | * 8  * *
xx. ... ox.&#x & ♦ 2  4 |  1  4  4 | 0  2  2 0 1 | * * 12 *
... oo.3ox.&#x & ♦ 1  3 |  0  3  3 | 0  0  3 1 0 | * *  * 8

x(ou)x x(xo)o3o(xo)x&#xt   → both heights = sqrt(5/12) = 0.645497
(trip || compound of pseudo {6} with perp pseudo u-line || gyro trip)

o(..). o(..).3o(..).     | 6 * * * | 1 2  2 1 0 0  0 0 0 0 | 2 1 2 2 1 2  2 0 0 0 0 0 0 | 1 2 1 1 2 1 0 0 0 0
.(o.). .(o.).3.(o.).     | * 6 * * | 0 0  2 0 1 1  2 0 0 0 | 0 0 1 2 2 0  2 1 2 2 0 0 0 | 0 1 1 0 2 2 1 1 0 0
.(.o). .(.o).3.(.o).     | * * 2 * | 0 0  0 3 0 0  0 3 0 0 | 0 0 0 0 0 3  6 0 0 0 3 0 0 | 0 0 0 1 3 3 0 0 1 0
.(..)o .(..)o3.(..)o     | * * * 6 | 0 0  0 0 0 0  2 1 1 2 | 0 0 0 0 0 0  2 2 1 2 2 2 1 | 0 0 0 0 1 2 1 2 1 1
-------------------------+---------+-----------------------+----------------------------+--------------------
x(..). .(..). .(..).     | 2 0 0 0 | 3 *  * * * *  * * * * | 2 0 2 0 0 0  0 0 0 0 0 0 0 | 1 2 1 0 0 0 0 0 0 0
.(..). x(..). .(..).     | 2 0 0 0 | * 6  * * * *  * * * * | 1 1 0 1 0 1  0 0 0 0 0 0 0 | 1 1 0 1 1 0 0 0 0 0
o(o.). o(o.).3o(o.).&#x  | 1 1 0 0 | * * 12 * * *  * * * * | 0 0 1 1 1 0  1 0 0 0 0 0 0 | 0 1 1 0 1 1 0 0 0 0
o(.o). o(.o).3o(.o).&#x  | 1 0 1 0 | * *  * 6 * *  * * * * | 0 0 0 0 0 2  2 0 0 0 0 0 0 | 0 0 0 1 2 1 0 0 0 0
.(..). .(x.). .(..).     | 0 2 0 0 | * *  * * 3 *  * * * * | 0 0 0 2 0 0  0 0 2 0 0 0 0 | 0 1 0 0 2 0 1 0 0 0
.(..). .(..). .(x.).     | 0 2 0 0 | * *  * * * 3  * * * * | 0 0 0 0 2 0  0 0 0 2 0 0 0 | 0 0 1 0 0 2 0 1 0 0
.(o.)o .(o.)o3.(o.)o&#x  | 0 1 0 1 | * *  * * * * 12 * * * | 0 0 0 0 0 0  1 1 1 1 0 0 0 | 0 0 0 0 1 1 1 1 0 0
.(.o)o .(.o)o3.(.o)o&#x  | 0 0 1 1 | * *  * * * *  * 6 * * | 0 0 0 0 0 0  2 0 0 0 2 0 0 | 0 0 0 0 1 2 0 0 1 0
.(..)x .(..). .(..).     | 0 0 0 2 | * *  * * * *  * * 3 * | 0 0 0 0 0 0  0 2 0 0 0 2 0 | 0 0 0 0 0 0 1 2 0 1
.(..). .(..). .(..)x     | 0 0 0 2 | * *  * * * *  * * * 6 | 0 0 0 0 0 0  0 0 0 1 1 1 1 | 0 0 0 0 0 1 0 1 1 1
-------------------------+---------+-----------------------+----------------------------+--------------------
x(..). x(..). .(..).     | 4 0 0 0 | 2 2  0 0 0 0  0 0 0 0 | 3 * * * * *  * * * * * * * | 1 1 0 0 0 0 0 0 0 0
.(..). x(..).3o(..).     | 3 0 0 0 | 0 3  0 0 0 0  0 0 0 0 | * 2 * * * *  * * * * * * * | 1 0 0 1 0 0 0 0 0 0
x(o.). .(..). .(..).&#x  | 2 1 0 0 | 1 0  2 0 0 0  0 0 0 0 | * * 6 * * *  * * * * * * * | 0 1 1 0 0 0 0 0 0 0
.(..). x(x.). .(..).&#x  | 2 2 0 0 | 0 1  2 0 1 0  0 0 0 0 | * * * 6 * *  * * * * * * * | 0 1 0 0 1 0 0 0 0 0
.(..). .(..). o(x.).&#x  | 1 2 0 0 | 0 0  2 0 0 1  0 0 0 0 | * * * * 6 *  * * * * * * * | 0 0 1 0 0 1 0 0 0 0
.(..). x(.o). .(..).&#x  | 2 0 1 0 | 0 1  0 2 0 0  0 0 0 0 | * * * * * 6  * * * * * * * | 0 0 0 1 1 0 0 0 0 0
o(oo)o o(oo)o3o(oo)o&#xr | 1 1 1 1 | 0 0  1 1 0 0  1 1 0 0 | * * * * * * 12 * * * * * * | 0 0 0 0 1 1 0 0 0 0
.(o.)x .(..). .(..).&#x  | 0 1 0 2 | 0 0  0 0 0 0  2 0 1 0 | * * * * * *  * 6 * * * * * | 0 0 0 0 0 0 1 1 0 0
.(..). .(x.)o .(..).&#x  | 0 2 0 1 | 0 0  0 0 1 0  2 0 0 0 | * * * * * *  * * 6 * * * * | 0 0 0 0 1 0 1 0 0 0
.(..). .(..). .(x.)x&#x  | 0 2 0 2 | 0 0  0 0 0 1  2 0 0 1 | * * * * * *  * * * 6 * * * | 0 0 0 0 0 1 0 1 0 0
.(..). .(..). .(.o)x&#x  | 0 0 1 2 | 0 0  0 0 0 0  0 2 0 1 | * * * * * *  * * * * 6 * * | 0 0 0 0 0 1 0 0 1 0
.(..)x .(..). .(..)x     | 0 0 0 4 | 0 0  0 0 0 0  0 0 2 2 | * * * * * *  * * * * * 3 * | 0 0 0 0 0 0 0 1 0 1
.(..). .(..)o3.(..)x     | 0 0 0 3 | 0 0  0 0 0 0  0 0 0 3 | * * * * * *  * * * * * * 2 | 0 0 0 0 0 0 0 0 1 1
-------------------------+---------+-----------------------+----------------------------+--------------------
x(..). x(..).3o(..).     ♦ 6 0 0 0 | 3 6  0 0 0 0  0 0 0 0 | 3 2 0 0 0 0  0 0 0 0 0 0 0 | 1 * * * * * * * * *
x(o.). x(x.). .(..).&#x  ♦ 4 2 0 0 | 2 2  4 0 1 0  0 0 0 0 | 1 0 2 2 0 0  0 0 0 0 0 0 0 | * 3 * * * * * * * *
x(o.). .(..). o(x.).&#x  ♦ 2 2 0 0 | 1 0  4 0 0 1  0 0 0 0 | 0 0 2 0 2 0  0 0 0 0 0 0 0 | * * 3 * * * * * * *
.(..). x(.o).3o(.o).&#x  ♦ 3 0 1 0 | 0 3  0 3 0 0  0 0 0 0 | 0 1 0 0 0 3  0 0 0 0 0 0 0 | * * * 2 * * * * * *
.(..). x(xo)o .(..).&#xr ♦ 2 2 1 1 | 0 1  2 2 1 0  2 1 0 0 | 0 0 0 1 0 1  2 0 1 0 0 0 0 | * * * * 6 * * * * *
.(..). .(..). o(xo)x&#xr ♦ 1 2 1 2 | 0 0  2 1 0 1  2 2 0 1 | 0 0 0 0 1 0  2 0 0 1 1 0 0 | * * * * * 6 * * * *
.(o.)x .(x.)o .(..).&#x  ♦ 0 2 0 2 | 0 0  0 0 1 0  4 0 1 0 | 0 0 0 0 0 0  0 2 2 0 0 0 0 | * * * * * * 3 * * *
.(o.)x .(..). .(x.)x&#x  ♦ 0 2 0 4 | 0 0  0 0 0 1  4 0 2 2 | 0 0 0 0 0 0  0 2 0 2 0 1 0 | * * * * * * * 3 * *
.(..). .(.o)o3.(.o)x&#x  ♦ 0 0 1 3 | 0 0  0 0 0 0  0 3 0 3 | 0 0 0 0 0 0  0 0 0 0 3 0 1 | * * * * * * * * 2 *
.(..)x .(..)o3.(..)x     ♦ 0 0 0 6 | 0 0  0 0 0 0  0 0 3 6 | 0 0 0 0 0 0  0 0 0 0 0 3 2 | * * * * * * * * * 1

(xoxxox)(uo) (oxxoxx)(ou)&#xr   → height(1,2) = height(3,7) = height(3,8) = height(4,5) = height(6,7) = height(6,8) = 1/sqrt(2) = 0.707107
                                  height(1,6) = height(1,7) = height(2,3) = height(2,8) = height(3,4) = height(3,8) = height(4,7) = height(5,6) = height(5,8) = sqrt(3)/2 = 0.866025

(o.....)(..) (o.....)(..)     | 2 * * * * * * * | 1 2 0 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 2 1 2 1 2 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 1 1 2 1 1 2 0 0 0 0 0 0 0 0 0 0
(.o....)(..) (.o....)(..)     | * 2 * * * * * * | 0 2 1 0 0 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 1 2 0 0 2 2 0 1 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 1 2 1 0 0 2 1 1 0 0 0 0 0 0 0 0
(..o...)(..) (..o...)(..)     | * * 4 * * * * * | 0 0 0 0 0 1 0 1 1 1 1 0 0 0 0 1 0 0 0 0 0 0 | 0 0 0 0 1 0 0 1 1 1 1 1 1 1 0 0 0 1 1 1 1 0 0 0 0 0 0 | 0 1 0 0 0 1 1 1 1 1 1 1 0 0 0 0
(...o..)(..) (...o..)(..)     | * * * 2 * * * * | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 1 0 0 1 2 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 1 2 2 2 0 0 0 2 1 | 0 0 0 0 0 0 0 0 1 2 1 2 1 0 0 1
(....o.)(..) (....o.)(..)     | * * * * 2 * * * | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 0 2 1 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 2 1 2 2 1 2 | 0 0 0 0 0 0 0 0 0 1 0 2 2 1 1 1
(.....o)(..) (.....o)(..)     | * * * * * 4 * * | 0 0 0 1 0 0 0 0 0 0 0 1 1 1 1 0 0 0 1 0 0 0 | 0 0 1 1 0 1 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 | 0 0 1 1 1 1 0 0 0 0 0 1 1 1 1 0
(......)(o.) (......)(o.)     | * * * * * * 2 * | 0 0 0 0 1 0 0 0 0 2 0 2 0 0 0 0 1 0 0 0 0 0 | 0 0 0 0 2 0 2 0 0 0 0 1 0 2 0 1 0 0 0 0 2 2 0 0 0 0 0 | 0 1 0 0 1 2 0 0 0 0 1 2 1 0 0 0
(......)(.o) (......)(.o)     | * * * * * * * 2 | 0 0 0 0 0 0 1 0 0 0 2 0 2 0 0 0 0 1 0 0 0 0 | 0 0 0 0 0 2 0 0 0 2 0 0 1 2 0 0 1 0 0 2 0 0 0 0 2 0 0 | 0 0 1 0 0 2 0 1 0 1 0 2 0 0 1 0
------------------------------+-----------------+---------------------------------------------+-------------------------------------------------------+--------------------------------
(x.....)(..) (......)(..)     | 2 0 0 0 0 0 0 0 | 1 * * * * * * * * * * * * * * * * * * * * * | 2 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 1 0 2 1 0 0 0 0 0 0 0 0 0 0 0 0
(oo....)(..) (oo....)(..)&#x  | 1 1 0 0 0 0 0 0 | * 4 * * * * * * * * * * * * * * * * * * * * | 1 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 1 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0
(......)(..) (.x....)(..)     | 0 2 0 0 0 0 0 0 | * * 1 * * * * * * * * * * * * * * * * * * * | 0 2 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 1 2 0 0 0 0 1 0 0 0 0 0 0 0 0 0
(o....o)(..) (o....o)(..)&#x  | 1 0 0 0 0 1 0 0 | * * * 4 * * * * * * * * * * * * * * * * * * | 0 0 1 1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0
(o.....)(o.) (o.....)(o.)&#x  | 1 0 0 0 0 0 1 0 | * * * * 2 * * * * * * * * * * * * * * * * * | 0 0 0 0 2 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 0 1 0 0 1 2 0 0 0 0 0 0 0 0 0 0
(.oo...)(..) (.oo...)(..)&#x  | 0 1 1 0 0 0 0 0 | * * * * * 4 * * * * * * * * * * * * * * * * | 0 0 0 0 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0
(.o....)(.o) (.o....)(.o)&#x  | 0 1 0 0 0 0 0 1 | * * * * * * 2 * * * * * * * * * * * * * * * | 0 0 0 0 0 2 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 0 0 1 0 0 2 0 1 0 0 0 0 0 0 0 0
(..x...)(..) (......)(..)     | 0 0 2 0 0 0 0 0 | * * * * * * * 2 * * * * * * * * * * * * * * | 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0
(......)(..) (..x...)(..)     | 0 0 2 0 0 0 0 0 | * * * * * * * * 2 * * * * * * * * * * * * * | 0 0 0 0 0 0 0 0 1 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 | 0 1 0 0 0 0 1 0 1 0 1 0 0 0 0 0
(..o...)(o.) (..o...)(o.)&#x  | 0 0 1 0 0 0 1 0 | * * * * * * * * * 4 * * * * * * * * * * * * | 0 0 0 0 1 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 | 0 1 0 0 0 1 0 0 0 0 1 1 0 0 0 0
(..o...)(.o) (..o...)(.o)&#x  | 0 0 1 0 0 0 0 1 | * * * * * * * * * * 4 * * * * * * * * * * * | 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 | 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0
(.....o)(o.) (.....o)(o.)&#x  | 0 0 0 0 0 1 1 0 | * * * * * * * * * * * 4 * * * * * * * * * * | 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 | 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0
(.....o)(.o) (.....o)(.o)&#x  | 0 0 0 0 0 1 0 1 | * * * * * * * * * * * * 4 * * * * * * * * * | 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0 0 | 0 0 1 0 0 1 0 0 0 0 0 1 0 0 1 0
(.....x)(..) (......)(..)     | 0 0 0 0 0 2 0 0 | * * * * * * * * * * * * * 2 * * * * * * * * | 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 | 0 0 1 1 0 0 0 0 0 0 0 0 0 1 1 0
(......)(..) (.....x)(..)     | 0 0 0 0 0 2 0 0 | * * * * * * * * * * * * * * 2 * * * * * * * | 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 | 0 0 0 1 1 0 0 0 0 0 0 0 1 1 0 0
(..oo..)(..) (..oo..)(..)&#x  | 0 0 1 1 0 0 0 0 | * * * * * * * * * * * * * * * 4 * * * * * * | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0
(...o..)(o.) (...o..)(o.)&#x  | 0 0 0 1 0 0 1 0 | * * * * * * * * * * * * * * * * 2 * * * * * | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 1 2 1 0 0 0
(....o.)(.o) (....o.)(.o)&#x  | 0 0 0 0 1 0 0 1 | * * * * * * * * * * * * * * * * * 2 * * * * | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 2 0 0 | 0 0 0 0 0 0 0 0 0 1 0 2 0 0 1 0
(....oo)(..) (....oo)(..)&#x  | 0 0 0 0 1 1 0 0 | * * * * * * * * * * * * * * * * * * 4 * * * | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 | 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0
(...x..)(..) (......)(..)     | 0 0 0 2 0 0 0 0 | * * * * * * * * * * * * * * * * * * * 1 * * | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 2 0 | 0 0 0 0 0 0 0 0 1 2 0 0 0 0 0 1
(...oo.)(..) (...oo.)(..)&#x  | 0 0 0 1 1 0 0 0 | * * * * * * * * * * * * * * * * * * * * 4 * | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 1 | 0 0 0 0 0 0 0 0 0 1 0 1 1 0 0 1
(......)(..) (....x.)(..)     | 0 0 0 0 2 0 0 0 | * * * * * * * * * * * * * * * * * * * * * 1 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 2 | 0 0 0 0 0 0 0 0 0 0 0 0 2 1 0 1
------------------------------+-----------------+---------------------------------------------+-------------------------------------------------------+--------------------------------
(xo....)(..) (......)(..)     | 2 1 0 0 0 0 0 0 | 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 2 * * * * * * * * * * * * * * * * * * * * * * * * * * | 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
(......)(..) (ox....)(..)     | 1 2 0 0 0 0 0 0 | 0 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | * 2 * * * * * * * * * * * * * * * * * * * * * * * * * | 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(x....x)(..) (......)(..)&#x  | 2 0 0 0 0 2 0 0 | 1 0 0 2 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 | * * 2 * * * * * * * * * * * * * * * * * * * * * * * * | 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0
(......)(..) (o....x)(..)&#x  | 1 0 0 0 0 2 0 0 | 0 0 0 2 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 | * * * 2 * * * * * * * * * * * * * * * * * * * * * * * | 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0
(ooo...)(o.) (ooo...)(o.)&#xr | 1 1 1 0 0 0 1 0 | 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 | * * * * 4 * * * * * * * * * * * * * * * * * * * * * * | 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 cycle (1237)
(oo...o)(.o) (oo...o)(.o)&#xr | 1 1 0 0 0 1 0 1 | 0 1 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 | * * * * * 4 * * * * * * * * * * * * * * * * * * * * * | 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 cycle (1286)
(o....o)(o.) (o....o)(o.)&#x  | 1 0 0 0 0 1 1 0 | 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 | * * * * * * 4 * * * * * * * * * * * * * * * * * * * * | 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0
(.ox...)(..) (......)(..)&#x  | 0 1 2 0 0 0 0 0 | 0 0 0 0 0 2 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | * * * * * * * 2 * * * * * * * * * * * * * * * * * * * | 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0
(......)(..) (.xx...)(..)&#x  | 0 2 2 0 0 0 0 0 | 0 0 1 0 0 2 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 | * * * * * * * * 2 * * * * * * * * * * * * * * * * * * | 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0
(.oo...)(.o) (.oo...)(.o)&#x  | 0 1 1 0 0 0 0 1 | 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 | * * * * * * * * * 4 * * * * * * * * * * * * * * * * * | 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0
(..x...)(..) (..x...)(..)     | 0 0 4 0 0 0 0 0 | 0 0 0 0 0 0 0 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 | * * * * * * * * * * 1 * * * * * * * * * * * * * * * * | 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0
(......)(..) (..x...)(o.)&#x  | 0 0 2 0 0 0 1 0 | 0 0 0 0 0 0 0 0 1 2 0 0 0 0 0 0 0 0 0 0 0 0 | * * * * * * * * * * * 2 * * * * * * * * * * * * * * * | 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0
(..x...)(.o) (......)(..)&#x  | 0 0 2 0 0 0 0 1 | 0 0 0 0 0 0 0 1 0 0 2 0 0 0 0 0 0 0 0 0 0 0 | * * * * * * * * * * * * 2 * * * * * * * * * * * * * * | 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0
(..o..o)(oo) (..o..o)(oo)&#x  | 0 0 1 0 0 1 1 1 | 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 | * * * * * * * * * * * * * 4 * * * * * * * * * * * * * | 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 cycle (3768)
(.....x)(..) (.....x)(..)     | 0 0 0 0 0 4 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 0 0 0 0 0 0 0 | * * * * * * * * * * * * * * 1 * * * * * * * * * * * * | 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0
(......)(..) (.....x)(o.)&#x  | 0 0 0 0 0 2 1 0 | 0 0 0 0 0 0 0 0 0 0 0 2 0 0 1 0 0 0 0 0 0 0 | * * * * * * * * * * * * * * * 2 * * * * * * * * * * * | 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0
(.....x)(.o) (......)(..)&#x  | 0 0 0 0 0 2 0 1 | 0 0 0 0 0 0 0 0 0 0 0 0 2 1 0 0 0 0 0 0 0 0 | * * * * * * * * * * * * * * * * 2 * * * * * * * * * * | 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0
(..xx..)(..) (......)(..)&#x  | 0 0 2 2 0 0 0 0 | 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 2 0 0 0 1 0 0 | * * * * * * * * * * * * * * * * * 2 * * * * * * * * * | 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0
(......)(..) (..xo..)(..)&#x  | 0 0 2 1 0 0 0 0 | 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 2 0 0 0 0 0 0 | * * * * * * * * * * * * * * * * * * 2 * * * * * * * * | 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0
(..ooo.)(.o) (..ooo.)(.o)&#xr | 0 0 1 1 1 0 0 1 | 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 1 0 | * * * * * * * * * * * * * * * * * * * 4 * * * * * * * | 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 cycle (3458)
(..oo..)(o.) (..oo..)(o.)&#x  | 0 0 1 1 0 0 1 0 | 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 | * * * * * * * * * * * * * * * * * * * * 4 * * * * * * | 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0
(...ooo)(o.) (...ooo)(o.)&#xr | 0 0 0 1 1 1 1 0 | 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 1 0 1 0 | * * * * * * * * * * * * * * * * * * * * * 4 * * * * * | 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 cycle (4567)
(....ox)(..) (......)(..)&#x  | 0 0 0 0 1 2 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 2 0 0 0 | * * * * * * * * * * * * * * * * * * * * * * 2 * * * * | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0
(......)(..) (....xx)(..)&#x  | 0 0 0 0 2 2 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 2 0 0 1 | * * * * * * * * * * * * * * * * * * * * * * * 2 * * * | 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0
(....oo)(.o) (....oo)(.o)&#x  | 0 0 0 0 1 1 0 1 | 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 | * * * * * * * * * * * * * * * * * * * * * * * * 4 * * | 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0
(...xo.)(..) (......)(..)&#x  | 0 0 0 2 1 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 0 | * * * * * * * * * * * * * * * * * * * * * * * * * 2 * | 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1
(......)(..) (...ox.)(..)&#x  | 0 0 0 1 2 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 1 | * * * * * * * * * * * * * * * * * * * * * * * * * * 2 | 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1
------------------------------+-----------------+---------------------------------------------+-------------------------------------------------------+--------------------------------
(xo....)(..) (ox....)(..)&#x  ♦ 2 2 0 0 0 0 0 0 | 1 4 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 1 * * * * * * * * * * * * * * *
(......)(..) (oxx...)(o.)&#xr ♦ 1 2 2 0 0 0 1 0 | 0 2 1 0 1 2 0 0 1 2 0 0 0 0 0 0 0 0 0 0 0 0 | 0 1 0 0 2 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | * 2 * * * * * * * * * * * * * * cycle (1237)
(xo...x)(.o) (......)(..)&#xr ♦ 2 1 0 0 0 2 0 1 | 1 2 0 2 0 0 1 0 0 0 0 0 2 1 0 0 0 0 0 0 0 0 | 1 0 1 0 0 2 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 | * * 2 * * * * * * * * * * * * * cycle (1286)
(x....x)(..) (o....x)(..)&#x  ♦ 2 0 0 0 0 4 0 0 | 1 0 0 4 0 0 0 0 0 0 0 0 0 2 2 0 0 0 0 0 0 0 | 0 0 2 2 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 | * * * 1 * * * * * * * * * * * *
(......)(..) (o....x)(o.)&#x  ♦ 1 0 0 0 0 2 1 0 | 0 0 0 2 1 0 0 0 0 0 0 2 0 0 1 0 0 0 0 0 0 0 | 0 0 0 1 0 0 2 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 | * * * * 2 * * * * * * * * * * *
(ooo..o)(oo) (ooo..o)(oo)&#xr ♦ 1 1 1 0 0 1 1 1 | 0 1 0 1 1 1 1 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 | 0 0 0 0 1 1 1 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 | * * * * * 4 * * * * * * * * * * cycles (167)(238)
(.ox...)(..) (.xx...)(..)&#x  ♦ 0 2 4 0 0 0 0 0 | 0 0 1 0 0 4 0 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 2 2 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | * * * * * * 1 * * * * * * * * *
(.ox...)(.o) (......)(..)&#x  ♦ 0 1 2 0 0 0 0 1 | 0 0 0 0 0 2 1 1 0 0 2 0 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 0 2 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | * * * * * * * 2 * * * * * * * *
(..xx..)(..) (..xo..)(..)&#x  ♦ 0 0 4 2 0 0 0 0 | 0 0 0 0 0 0 0 2 2 0 0 0 0 0 0 4 0 0 0 1 0 0 | 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 2 2 0 0 0 0 0 0 0 0 | * * * * * * * * 1 * * * * * * *
(..xxo.)(.o) (......)(..)&#xr ♦ 0 0 2 2 1 0 0 1 | 0 0 0 0 0 0 0 1 0 0 2 0 0 0 0 2 0 1 0 1 2 0 | 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 2 0 0 0 0 0 1 0 | * * * * * * * * * 2 * * * * * * cycle (3458)
(......)(..) (..xo..)(o.)&#x  ♦ 0 0 2 1 0 0 1 0 | 0 0 0 0 0 0 0 0 1 2 0 0 0 0 0 2 1 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 2 0 0 0 0 0 0 | * * * * * * * * * * 2 * * * * *
(..oooo)(oo) (..oooo)(oo)&#xr ♦ 0 0 1 1 1 1 1 1 | 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 1 1 1 1 0 1 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 1 0 0 | * * * * * * * * * * * 4 * * * * cycles (347)(568)
(......)(..) (...oxx)(o.)&#xr ♦ 0 0 0 1 2 2 1 0 | 0 0 0 0 0 0 0 0 0 0 0 2 0 0 1 0 1 0 2 0 2 1 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 2 0 1 0 0 1 | * * * * * * * * * * * * 2 * * * cycle (4567)
(....ox)(..) (....xx)(..)&#x  ♦ 0 0 0 0 2 4 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 0 0 0 4 0 0 1 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 2 2 0 0 0 | * * * * * * * * * * * * * 1 * *
(....ox)(.o) (......)(..)&#x  ♦ 0 0 0 0 1 2 0 1 | 0 0 0 0 0 0 0 0 0 0 0 0 2 1 0 0 0 1 2 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 2 0 0 | * * * * * * * * * * * * * * 2 *
(...xo.)(..) (...ox.)(..)&#x  ♦ 0 0 0 2 2 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 4 1 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 | * * * * * * * * * * * * * * * 1