|
Acronym
|
tepe, K-4.9 (alt: dycuf)
|
|
Name
|
tetrahedron prism,
line || trip,
square - square bi-wedge,
digonal orthobicupolaic ring,
vertex figure of rix,
dyadic cupolafastegium,
equatorial cross-section of tet-first hin
|
|
|,>,O device
|
line pyramid pyramid prism = |>>|
|
|
|
 © ©
|
Segmentochoron display /
VRML
|
⭳ ⭳ ⭳  © ©
|
|
Cross sections
|
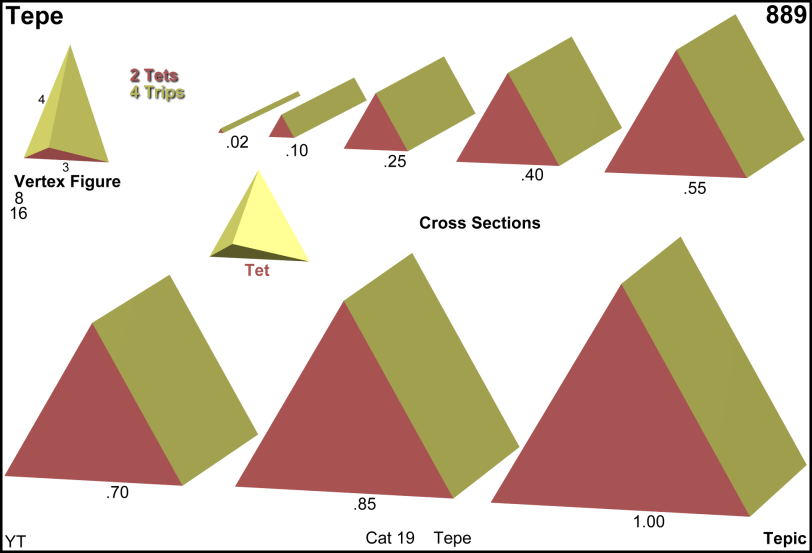 © ©
|
|
Circumradius
|
sqrt(5/8) = 0.790569
|
Lace city
in approx. ASCII-art
|
x x
x o x o
|
o x o x
x o x o
|
o3o o3o
x3o x3o
|
|
Coordinates
|
(1/sqrt(8), 1/sqrt(8), 1/sqrt(8), 1/2) & all even permutations and all even changes of sign in all but last coord., change of sign in last coord.
|
|
Volume
|
sqrt(2)/12 = 0.117851
|
|
Dihedral angles
|
- at {3} between tet and trip: 90°
- at {4} between trip and trip: arccos(1/3) = 70.528779°
|
|
Face vector
|
8, 16, 14, 6
|
|
Confer
|
- variations:
-
q x3o3o
f x3o3o
- more general:
-
n-cuf
- blends:
-
tutepe
- ambification:
-
retepe
- general polytopal classes:
-
Wythoffian polychora
segmentochora
lace simplices
|
External
links
|



|
Incidence matrix according to Dynkin symbol
x x3o3o
. . . . | 8 ♦ 1 3 | 3 3 | 3 1
--------+---+------+-----+----
x . . . | 2 | 4 * | 3 0 | 3 0
. x . . | 2 | * 12 | 1 2 | 2 1
--------+---+------+-----+----
x x . . | 4 | 2 2 | 6 * | 2 0
. x3o . | 3 | 0 3 | * 8 | 1 1
--------+---+------+-----+----
x x3o . ♦ 6 | 3 6 | 3 2 | 4 *
. x3o3o ♦ 4 | 0 6 | 0 4 | * 2
x x3o3/2o
. . . . | 8 ♦ 1 3 | 3 3 | 3 1
----------+---+------+-----+----
x . . . | 2 | 4 * | 3 0 | 3 0
. x . . | 2 | * 12 | 1 2 | 2 1
----------+---+------+-----+----
x x . . | 4 | 2 2 | 6 * | 2 0
. x3o . | 3 | 0 3 | * 8 | 1 1
----------+---+------+-----+----
x x3o . ♦ 6 | 3 6 | 3 2 | 4 *
. x3o3/2o ♦ 4 | 0 6 | 0 4 | * 2
x x3/2o3o
. . . . | 8 ♦ 1 3 | 3 3 | 3 1
----------+---+------+-----+----
x . . . | 2 | 4 * | 3 0 | 3 0
. x . . | 2 | * 12 | 1 2 | 2 1
----------+---+------+-----+----
x x . . | 4 | 2 2 | 6 * | 2 0
. x3/2o . | 3 | 0 3 | * 8 | 1 1
----------+---+------+-----+----
x x3/2o . ♦ 6 | 3 6 | 3 2 | 4 *
. x3/2o3o ♦ 4 | 0 6 | 0 4 | * 2
x x3/2o3/2o
. . . . | 8 ♦ 1 3 | 3 3 | 3 1
------------+---+------+-----+----
x . . . | 2 | 4 * | 3 0 | 3 0
. x . . | 2 | * 12 | 1 2 | 2 1
------------+---+------+-----+----
x x . . | 4 | 2 2 | 6 * | 2 0
. x3/2o . | 3 | 0 3 | * 8 | 1 1
------------+---+------+-----+----
x x3/2o . ♦ 6 | 3 6 | 3 2 | 4 *
. x3/2o3/2o ♦ 4 | 0 6 | 0 4 | * 2
x o3o4s
. demi( . . . ) | 8 ♦ 1 3 | 3 3 | 3 1
----------------+---+------+-----+----
x demi( . . . ) | 2 | 4 * | 3 0 | 3 0
. . o4s | 2 | * 12 | 1 2 | 2 1
----------------+---+------+-----+----
x . o4s | 4 | 2 2 | 6 * | 2 0
. sefa( o3o4s ) | 3 | 0 3 | * 8 | 1 1
----------------+---+------+-----+----
x sefa( o3o4s ) ♦ 6 | 3 6 | 3 2 | 4 *
. o3o4s ♦ 4 | 0 6 | 0 4 | * 2
x s2s4o
. demi( . . . ) | 8 ♦ 1 2 1 | 2 1 3 | 1 3
----------------+---+-------+-------+----
x demi( . . . ) | 2 | 4 * * | 2 1 0 | 0 3
. s2s . | 2 | * 8 * | 1 0 2 | 1 2
. . s4o | 2 | * * 4 | 0 1 2 | 1 2
----------------+---+-------+-------+----
x s2s . | 4 | 2 2 0 | 4 * * | 0 2
x . s4o | 4 | 2 0 2 | * 2 * | 0 2
. sefa( s2s4o ) | 3 | 0 2 1 | * * 8 | 1 1
----------------+---+-------+-------+----
. s2s4o ♦ 4 | 0 4 2 | 0 0 4 | 2 *
x sefa( s2s4o ) ♦ 6 | 3 4 2 | 2 1 2 | * 4
x s2s2s
. demi( . . . ) | 8 ♦ 1 1 1 1 | 1 1 1 3 | 3 1
----------------+---+---------+---------+----
x demi( . . . ) | 2 | 4 * * * | 1 1 1 0 | 3 0
. s2s . | 2 | * 4 * * | 1 0 0 2 | 2 1
. s 2 s | 2 | * * 4 * | 0 1 0 2 | 2 1
. . s2s | 2 | * * * 4 | 0 0 1 2 | 2 1
----------------+---+---------+---------+----
x s2s . | 4 | 2 2 0 0 | 2 * * * | 2 0
x s 2 s | 4 | 2 0 2 0 | * 2 * * | 2 0
x . s2s | 4 | 2 0 0 2 | * * 2 * | 2 0
. sefa( s2s2s ) | 3 | 0 1 1 1 | * * * 8 | 1 1
----------------+---+---------+---------+----
x sefa( s2s2s ) ♦ 6 | 3 2 2 2 | 1 1 1 2 | 4 *
. s2s2s ♦ 4 | 0 2 2 2 | 0 0 0 4 | * 2
x2o3o4s
demi( . . . . ) | 8 ♦ 1 3 | 3 3 | 1 3
----------------+---+------+-----+----
demi( x . . . ) | 2 | 4 * | 3 0 | 0 3
. . o4s | 2 | * 12 | 1 2 | 1 2
----------------+---+------+-----+----
x 2 o4s | 4 | 2 2 | 6 * | 0 2
sefa( . o3o4s ) | 3 | 0 3 | * 8 | 1 1
----------------+---+------+-----+----
. o3o4s ♦ 4 | 0 6 | 0 4 | 2 *
sefa( x2o3o4s ) ♦ 6 | 3 6 | 3 2 | * 4
starting figure: x o3o4x
x2s2s4o
demi( . . . . ) | 8 ♦ 1 2 1 | 2 1 3 | 1 3
----------------+---+-------+-------+----
demi( x . . . ) | 2 | 4 * * | 2 1 0 | 0 3
. s2s . | 2 | * 8 * | 1 0 2 | 1 2
. . s4o | 2 | * * 4 | 0 1 2 | 1 2
----------------+---+-------+-------+----
x2s2s . | 4 | 2 2 0 | 4 * * | 0 2
x 2 s4o | 4 | 2 0 2 | * 2 * | 0 2
sefa( . s2s4o ) | 3 | 0 2 1 | * * 8 | 1 1
----------------+---+-------+-------+----
. s2s4o ♦ 4 | 0 4 2 | 0 0 4 | 2 *
sefa( x2s2s4o ) ♦ 6 | 3 4 2 | 2 1 2 | * 4
starting figure: x x x4o
x2s2s2s
demi( . . . . ) | 8 ♦ 1 1 1 1 | 1 1 1 3 | 1 3
----------------+---+---------+---------+----
demi( x . . . ) | 2 | 4 * * * | 1 1 1 0 | 0 3
. s2s . | 2 | * 4 * * | 1 0 0 2 | 1 2
. s 2 s | 2 | * * 4 * | 0 1 0 2 | 1 2
. . s2s | 2 | * * * 4 | 0 0 1 2 | 1 2
----------------+---+---------+---------+----
x2s2s . | 4 | 2 2 0 0 | 2 * * * | 0 2
x2s 2 s | 4 | 2 0 2 0 | * 2 * * | 0 2
x 2 s2s | 4 | 2 0 0 2 | * * 2 * | 0 2
sefa( . s2s2s ) | 3 | 0 1 1 1 | * * * 8 | 1 1
----------------+---+---------+---------+----
. s2s2s ♦ 4 | 0 2 2 2 | 0 0 0 4 | 2 *
sefa( x s2s2s ) ♦ 6 | 3 2 2 2 | 1 1 1 2 | * 4
starting figure: x x x x
xx3oo3oo&#x → height = 1
(tet || tet)
o.3o.3o. | 4 * ♦ 3 1 0 | 3 3 0 | 1 3 0
.o3.o3.o | * 4 ♦ 0 1 3 | 0 3 3 | 0 3 1
------------+-----+-------+-------+------
x. .. .. | 2 0 | 6 * * | 2 1 0 | 1 2 0
oo3oo3oo&#x | 1 1 | * 4 * | 0 3 0 | 0 3 0
.x .. .. | 0 2 | * * 6 | 0 1 2 | 0 2 1
------------+-----+-------+-------+------
x.3o. .. | 3 0 | 3 0 0 | 4 * * | 1 1 0
xx .. ..&#x | 2 2 | 1 2 1 | * 6 * | 0 2 0
.x3.o .. | 0 3 | 0 0 3 | * * 4 | 0 1 1
------------+-----+-------+-------+------
x.3o.3o. ♦ 4 0 | 6 0 0 | 4 0 0 | 1 * *
xx3oo ..&#x ♦ 3 3 | 3 3 3 | 1 3 1 | * 4 *
.x3.o3.o ♦ 0 4 | 0 0 6 | 0 0 4 | * * 1
xx ox3oo&#x → height = sqrt(2/3) = 0.816497
(line || para trip)
o. o.3o. | 2 * ♦ 1 3 0 0 | 3 3 0 0 | 3 1 0
.o .o3.o | * 6 ♦ 0 1 1 2 | 1 2 2 1 | 2 1 1
------------+-----+---------+---------+------
x. .. .. | 2 0 | 1 * * * | 3 0 0 0 | 3 0 0
oo oo3oo&#x | 1 1 | * 6 * * | 1 2 0 0 | 2 1 0
.x .. .. | 0 2 | * * 3 * | 1 0 2 0 | 2 0 1
.. .x .. | 0 2 | * * * 6 | 0 1 1 1 | 1 1 1
------------+-----+---------+---------+------
xx .. ..&#x | 2 2 | 1 2 1 0 | 3 * * * | 2 0 0
.. ox ..&#x | 1 2 | 0 2 0 1 | * 6 * * | 1 1 0
.x .x .. | 0 4 | 0 0 2 2 | * * 3 * | 1 0 1
.. .x3.o | 0 3 | 0 0 0 3 | * * * 2 | 0 1 1
------------+-----+---------+---------+------
xx ox ..&#x ♦ 2 4 | 1 4 2 2 | 2 2 1 0 | 3 * *
.. ox3oo&#x ♦ 1 3 | 0 3 0 3 | 0 3 0 1 | * 2 *
.x .x3.o ♦ 0 6 | 0 0 3 6 | 0 0 3 2 | * * 1
xx xo ox&#x → height = 1/sqrt(2) = 0.707107
({4} || ortho {4})
o. o. o. | 4 * ♦ 1 1 2 0 0 | 1 2 2 1 0 | 2 1 1
.o .o .o | * 4 ♦ 0 0 2 1 1 | 0 2 1 2 1 | 1 2 1
------------+-----+-----------+-----------+------
x. .. .. | 2 0 | 2 * * * * | 1 2 0 0 0 | 2 1 0
.. x. .. | 2 0 | * 2 * * * | 1 0 2 0 0 | 2 0 1
oo oo oo&#x | 1 1 | * * 8 * * | 0 1 1 1 0 | 1 1 1
.x .. .. | 0 2 | * * * 2 * | 0 2 0 0 1 | 1 2 0
.. .. .x | 0 2 | * * * * 2 | 0 0 0 2 1 | 0 2 1
------------+-----+-----------+-----------+------
x. x. .. | 4 0 | 2 2 0 0 0 | 1 * * * * | 2 0 0
xx .. ..&#x | 2 2 | 1 0 2 1 0 | * 4 * * * | 1 1 0
.. xo ..&#x | 2 1 | 0 1 2 0 0 | * * 4 * * | 1 0 1
.. .. ox&#x | 1 2 | 0 0 2 0 1 | * * * 4 * | 0 1 1
.x .. .x | 0 4 | 0 0 0 2 2 | * * * * 1 | 0 2 0
------------+-----+-----------+-----------+------
xx xo ..&#x ♦ 4 2 | 2 2 4 1 0 | 1 2 2 0 0 | 2 * *
xx .. ox&#x ♦ 2 4 | 1 0 4 2 2 | 0 2 0 2 1 | * 2 *
.. xo ox&#x ♦ 2 2 | 0 1 4 0 1 | 0 0 2 2 0 | * * 2
or
o. o. o. & | 8 ♦ 1 1 2 | 1 2 3 | 3 1
--------------+---+-------+-------+----
x. .. .. & | 2 | 4 * * | 1 2 0 | 3 0
.. x. .. & | 2 | * 4 * | 1 0 2 | 2 1
oo oo oo&#x | 2 | * * 8 | 0 1 2 | 2 1
--------------+---+-------+-------+----
x. x. .. & | 4 | 2 2 0 | 2 * * | 2 0
xx .. ..&#x | 4 | 2 0 2 | * 4 * | 2 0
.. xo ..&#x & | 3 | 0 1 2 | * * 8 | 1 1
--------------+---+-------+-------+----
xx xo ..&#x & ♦ 6 | 3 2 4 | 1 2 2 | 4 *
.. xo ox&#x ♦ 4 | 0 2 4 | 0 0 4 | * 2
oox xxx&#x → height(1,2) = 1
height(1,3) = height(2,3) = sqrt(3)/2 = 0.866025
o.. o.. | 2 * * ♦ 1 1 2 0 0 0 0 | 1 1 2 2 0 0 0 | 1 1 2 0
.o. .o. | * 2 * ♦ 0 1 0 1 2 0 0 | 1 0 0 2 1 2 0 | 0 1 2 1
..o ..o | * * 4 ♦ 0 0 1 0 1 1 1 | 0 1 1 1 1 1 1 | 1 1 1 1
-----------+-------+---------------+---------------+--------
... x.. | 2 0 0 | 1 * * * * * * | 1 0 2 0 0 0 0 | 1 0 2 0
oo. oo.&#x | 1 1 0 | * 2 * * * * * | 1 0 0 2 0 0 0 | 0 1 2 0
o.o o.o&#x | 1 0 1 | * * 4 * * * * | 0 1 1 1 0 0 0 | 1 1 1 0
... .x. | 0 2 0 | * * * 1 * * * | 1 0 0 0 0 2 0 | 0 0 2 1
.oo .oo&#x | 0 1 1 | * * * * 4 * * | 0 0 0 1 1 1 0 | 0 1 1 1
..x ... | 0 0 2 | * * * * * 2 * | 0 1 0 0 1 0 1 | 1 1 0 1
... ..x | 0 0 2 | * * * * * * 2 | 0 0 1 0 0 1 1 | 1 0 1 1
-----------+-------+---------------+---------------+--------
... xx.&#x | 2 2 0 | 1 2 0 1 0 0 0 | 1 * * * * * * | 0 0 2 0
o.x ...&#x | 1 0 2 | 0 0 2 0 0 1 0 | * 2 * * * * * | 1 1 0 0
... x.x&#x | 2 0 2 | 1 0 2 0 0 0 1 | * * 2 * * * * | 1 0 1 0
ooo ooo&#x | 1 1 1 | 0 1 1 0 1 0 0 | * * * 4 * * * | 0 1 1 0
.ox ...&#x | 0 1 2 | 0 0 0 0 2 1 0 | * * * * 2 * * | 0 1 0 1
... .xx&#x | 0 2 2 | 0 0 0 1 2 0 1 | * * * * * 2 * | 0 0 1 1
..x ..x | 0 0 4 | 0 0 0 0 0 2 2 | * * * * * * 1 | 1 0 0 1
-----------+-------+---------------+---------------+--------
o.x x.x&#x ♦ 2 0 4 | 1 0 4 0 0 2 2 | 0 2 2 0 0 0 1 | 1 * * *
oox ...&#x ♦ 1 1 2 | 0 1 2 0 2 1 0 | 0 1 0 2 1 0 0 | * 2 * *
... xxx&#x ♦ 2 2 2 | 1 2 2 1 2 0 1 | 1 0 1 2 0 1 0 | * * 2 *
.ox .xx&#x ♦ 0 2 4 | 0 0 0 1 4 2 2 | 0 0 0 0 2 2 1 | * * * 1
or
o.. o.. & | 4 * ♦ 1 1 2 0 0 | 1 1 2 2 0 | 1 1 2
..o ..o | * 4 ♦ 0 0 2 1 1 | 0 2 2 1 1 | 2 1 1
-------------+-----+-----------+-----------+------
... x.. & | 2 0 | 2 * * * * | 1 0 2 0 0 | 1 0 2
oo. oo.&#x | 2 0 | * 2 * * * | 1 0 0 2 0 | 0 1 2
o.o o.o&#x & | 1 1 | * * 8 * * | 0 1 1 1 0 | 1 1 1
..x ... | 0 2 | * * * 2 * | 0 2 0 0 1 | 2 1 0
... ..x | 0 2 | * * * * 2 | 0 0 2 0 1 | 2 0 1
-------------+-----+-----------+-----------+------
... xx.&#x | 4 0 | 2 2 0 0 0 | 1 * * * * | 0 0 2
o.x ...&#x & | 1 2 | 0 0 2 1 0 | * 4 * * * | 1 1 0
... x.x&#x & | 2 2 | 1 0 2 0 1 | * * 4 * * | 1 0 1
ooo ooo&#x | 2 1 | 0 1 2 0 0 | * * * 4 * | 0 1 1
..x ..x | 0 4 | 0 0 0 2 2 | * * * * 1 | 2 0 0
-------------+-----+-----------+-----------+------
o.x x.x&#x & ♦ 2 4 | 1 0 4 2 2 | 0 2 2 0 1 | 2 * *
oox ...&#x ♦ 2 2 | 0 1 4 1 0 | 0 2 0 2 0 | * 2 *
... xxx&#x ♦ 4 2 | 2 2 4 0 1 | 1 0 2 2 0 | * * 2
xxxx&#x → all pairwise heights = 1
o... | 2 * * * ♦ 1 1 1 1 0 0 0 0 0 0 | 1 1 1 1 1 1 0 0 0 0 | 1 1 1 1 0
.o.. | * 2 * * ♦ 0 1 0 0 1 1 1 0 0 0 | 1 1 1 0 0 0 1 1 1 0 | 1 1 1 0 1
..o. | * * 2 * ♦ 0 0 1 0 0 1 0 1 1 0 | 0 1 0 1 1 0 1 1 0 1 | 1 1 0 1 1
...o | * * * 2 ♦ 0 0 0 1 0 0 1 0 1 1 | 0 0 1 0 1 1 0 1 1 1 | 0 1 1 1 1
--------+---------+---------------------+---------------------+----------
x... | 2 0 0 0 | 1 * * * * * * * * * | 1 0 0 1 0 1 0 0 0 0 | 1 0 1 1 0
oo..&#x | 1 1 0 0 | * 2 * * * * * * * * | 1 1 1 0 0 0 0 0 0 0 | 1 1 1 0 0
o.o.&#x | 1 0 1 0 | * * 2 * * * * * * * | 0 1 0 1 1 0 0 0 0 0 | 1 1 0 1 0
o..o&#x | 1 0 0 1 | * * * 2 * * * * * * | 0 0 1 0 1 1 0 0 0 0 | 0 1 1 1 0
.x.. | 0 2 0 0 | * * * * 1 * * * * * | 1 0 0 0 0 0 1 0 1 0 | 1 0 1 0 1
.oo.&#x | 0 1 1 0 | * * * * * 2 * * * * | 0 1 0 0 0 0 1 1 0 0 | 1 1 0 0 1
.o.o&#x | 0 1 0 1 | * * * * * * 2 * * * | 0 0 1 0 0 0 0 1 1 0 | 0 1 1 0 1
..x. | 0 0 2 0 | * * * * * * * 1 * * | 0 0 0 1 0 0 1 0 0 1 | 1 0 0 1 1
..oo&#x | 0 0 1 1 | * * * * * * * * 2 * | 0 0 0 0 1 0 0 1 0 1 | 0 1 0 1 1
...x | 0 0 0 2 | * * * * * * * * * 1 | 0 0 0 0 0 1 0 0 1 1 | 0 0 1 1 1
--------+---------+---------------------+---------------------+----------
xx..&#x | 2 2 0 0 | 1 2 0 0 1 0 0 0 0 0 | 1 * * * * * * * * * | 1 0 1 0 0
ooo.&#x | 1 1 1 0 | 0 1 1 0 0 1 0 0 0 0 | * 2 * * * * * * * * | 1 1 0 0 0
oo.o&#x | 1 1 0 1 | 0 1 0 1 0 0 1 0 0 0 | * * 2 * * * * * * * | 0 1 1 0 0
x.x.&#x | 2 0 2 0 | 1 0 2 0 0 0 0 1 0 0 | * * * 1 * * * * * * | 1 0 0 1 0
o.oo&#x | 1 0 1 1 | 0 0 1 1 0 0 0 0 1 0 | * * * * 2 * * * * * | 0 1 0 1 0
x..x&#x | 2 0 0 2 | 1 0 0 2 0 0 0 0 0 1 | * * * * * 1 * * * * | 0 0 1 1 0
.xx.&#x | 0 2 2 0 | 0 0 0 0 1 2 0 1 0 0 | * * * * * * 1 * * * | 1 0 0 0 1
.ooo&#x | 0 1 1 1 | 0 0 0 0 0 1 1 0 1 0 | * * * * * * * 2 * * | 0 1 0 0 1
.x.x&#x | 0 2 0 2 | 0 0 0 0 1 0 2 0 0 1 | * * * * * * * * 1 * | 0 0 1 0 1
..xx&#x | 0 0 2 2 | 0 0 0 0 0 0 0 1 2 1 | * * * * * * * * * 1 | 0 0 0 1 1
--------+---------+---------------------+---------------------+----------
xxx.&#x ♦ 2 2 2 0 | 1 2 2 0 1 2 0 1 0 0 | 1 2 0 1 0 0 1 0 0 0 | 1 * * * *
oooo&#x ♦ 1 1 1 1 | 0 1 1 1 0 1 1 0 1 0 | 0 1 1 0 1 0 0 1 0 0 | * 2 * * *
xx.x&#x ♦ 2 2 0 2 | 1 2 0 2 1 0 2 0 0 1 | 1 0 2 0 0 1 0 0 1 0 | * * 1 * *
x.xx&#x ♦ 2 0 2 2 | 1 0 2 2 0 0 0 1 2 1 | 0 0 0 1 2 1 0 0 0 1 | * * * 1 *
.xxx&#x ♦ 0 2 2 2 | 0 0 0 0 1 2 2 1 2 1 | 0 0 0 0 0 0 1 2 1 1 | * * * * 1
xxoo ooxx&#xr → height(1,2) = height(3,4) = 1
height(2,3) = height(4,1) = sqrt(3)/2 = 0.866025
(line || (para line || perp line) || perp line)
o(..). o(..). | 2 * * * ♦ 1 1 2 0 0 0 0 0 | 1 2 1 2 0 0 0 | 1 2 1 0
.(o.). .(o.). | * 2 * * ♦ 0 1 0 1 2 0 0 0 | 1 0 0 2 2 1 0 | 0 2 1 1
.(.o). .(.o). | * * 2 * ♦ 0 0 2 0 0 1 1 0 | 0 1 2 2 0 0 1 | 1 1 2 0
.(..)o .(..)o | * * * 2 ♦ 0 0 0 0 2 0 1 1 | 0 0 0 2 1 2 1 | 0 1 2 1
-----------------+---------+-----------------+---------------+--------
x(..). .(..). | 2 0 0 0 | 1 * * * * * * * | 1 2 0 0 0 0 0 | 1 2 0 0
o(o.). o(o.).&#x | 1 1 0 0 | * 2 * * * * * * | 1 0 0 2 0 0 0 | 0 2 1 0
o(.o). o(.o).&#x | 1 0 1 0 | * * 4 * * * * * | 0 1 1 1 0 0 0 | 1 1 1 0
.(x.). .(..). | 0 2 0 0 | * * * 1 * * * * | 1 0 0 0 2 0 0 | 0 2 0 1
.(o.)o .(o.)o&#x | 0 1 0 1 | * * * * 4 * * * | 0 0 0 1 1 1 0 | 0 1 1 1
.(..). .(.x). | 0 0 2 0 | * * * * * 1 * * | 0 0 2 0 0 0 1 | 1 0 2 0
.(.o)o .(.o)o&#x | 0 0 1 1 | * * * * * * 2 * | 0 0 0 2 0 0 1 | 0 1 2 0
.(..). .(..)x | 0 0 0 2 | * * * * * * * 1 | 0 0 0 0 0 2 1 | 0 0 2 1
-----------------+---------+-----------------+---------------+--------
x(x.). .(..).&#x | 2 2 0 0 | 1 2 0 1 0 0 0 0 | 1 * * * * * * | 0 2 0 0
x(.o). .(..).&#x | 2 0 1 0 | 1 0 2 0 0 0 0 0 | * 2 * * * * * | 1 1 0 0
.(..). o(.x).&#x | 1 0 2 0 | 0 0 2 0 0 1 0 0 | * * 2 * * * * | 1 0 1 0
oooo oooo&#xr | 1 1 1 1 | 0 1 1 0 1 0 1 0 | * * * 4 * * * | 0 1 1 0
.(x.)o .(..).&#x | 0 2 0 1 | 0 0 0 1 2 0 0 0 | * * * * 2 * * | 0 1 0 1
.(..). .(o.)x&#x | 0 1 0 2 | 0 0 0 0 2 0 0 1 | * * * * * 2 * | 0 0 1 1
.(..). .(.x)x&#x | 0 0 2 2 | 0 0 0 0 0 1 2 1 | * * * * * * 1 | 0 0 2 0
-----------------+---------+-----------------+---------------+--------
x(.o). o(.x).&#x ♦ 2 0 2 0 | 1 0 4 0 0 1 0 0 | 0 2 2 0 0 0 0 | 1 * * *
xxoo ....&#xr ♦ 2 2 1 1 | 1 2 2 1 2 0 1 0 | 1 1 0 2 1 0 0 | * 2 * *
.... ooxx&#xr ♦ 1 1 2 2 | 0 1 2 0 2 1 2 1 | 0 0 1 2 0 1 1 | * * 2 *
.(x.)o .(o.)x&#x ♦ 0 2 0 2 | 0 0 0 1 4 0 0 1 | 0 0 0 0 2 2 0 | * * * 1
or
o(..). o(..). & | 4 * ♦ 1 1 2 0 | 1 2 1 2 | 1 3
.(o.). .(o.). & | * 4 ♦ 0 1 2 1 | 1 1 2 2 | 1 3
-------------------+-----+---------+---------+----
x(..). .(..). & | 2 0 | 2 * * * | 1 2 0 0 | 1 2
o(o.). o(o.).&#x & | 1 1 | * 4 * * | 1 0 0 2 | 0 3
o(.o). o(.o).&#x & | 1 1 | * * 8 * | 0 1 1 1 | 1 2
.(x.). .(..). & | 0 2 | * * * 2 | 1 0 2 0 | 1 2
-------------------+-----+---------+---------+----
x(x.). .(..).&#x & | 2 2 | 1 2 0 1 | 2 * * * | 0 2
x(.o). .(..).&#x & | 2 1 | 1 0 2 0 | * 4 * * | 1 1
.(..). o(.x).&#x & | 1 2 | 0 0 2 1 | * * 4 * | 1 1
oooo oooo&#xr | 2 2 | 0 2 2 0 | * * * 4 | 0 2
-------------------+-----+---------+---------+----
x(.o). o(.x).&#x & ♦ 2 2 | 1 0 4 1 | 0 2 2 0 | 2 *
xxoo ....&#xr & ♦ 3 3 | 1 3 4 1 | 1 1 1 2 | * 4
oxxo3oooo&#xr → height(2,3) = height(4,1) = 1
height(1,2) = height(3,4) = sqrt(2/3) = 0.816497
(type: (pt || {3}) || (pt || {3}) )
o...3o... | 1 * * * ♦ 3 1 0 0 0 0 | 3 3 0 0 0 0 | 1 3 0 0
.o..3.o.. | * 3 * * ♦ 1 0 2 1 0 0 | 2 1 1 2 0 0 | 1 2 1 0
..o.3..o. | * * 3 * ♦ 0 0 0 1 2 1 | 0 1 0 2 1 2 | 0 2 1 1
...o3...o | * * * 1 ♦ 0 1 0 0 0 3 | 0 3 0 0 0 3 | 0 3 0 1
--------------+---------+-------------+-------------+--------
oo..3oo..&#x | 1 1 0 0 | 3 * * * * * | 2 1 0 0 0 0 | 1 2 0 0
o..o3o..o&#x | 1 0 0 1 | * 1 * * * * | 0 3 0 0 0 0 | 0 3 0 0
.x.. .... | 0 2 0 0 | * * 3 * * * | 1 0 1 1 0 0 | 1 1 1 0
.oo.3.oo.&#x | 0 1 1 0 | * * * 3 * * | 0 1 0 2 0 0 | 0 2 1 0
..x. .... | 0 0 2 0 | * * * * 3 * | 0 0 0 1 1 1 | 0 1 1 1
..oo3..oo&#x | 0 0 1 1 | * * * * * 3 | 0 1 0 0 0 2 | 0 2 0 1
--------------+---------+-------------+-------------+--------
ox.. ....&#x | 1 2 0 0 | 2 0 1 0 0 0 | 3 * * * * * | 1 1 0 0
oooo3oooo&#xr | 1 1 1 1 | 1 1 0 1 0 1 | * 3 * * * * | 0 2 0 0
.x..3.o.. | 0 3 0 0 | 0 0 3 0 0 0 | * * 1 * * * | 1 0 1 0
.xx. ....&#x | 0 2 2 0 | 0 0 1 2 1 0 | * * * 3 * * | 0 1 1 0
..x.3..o. | 0 0 3 0 | 0 0 0 0 3 0 | * * * * 1 * | 0 0 1 1
..xo ....&#x | 0 0 2 1 | 0 0 0 0 1 2 | * * * * * 3 | 0 1 0 1
--------------+---------+-------------+-------------+--------
ox..3oo..&#x ♦ 1 3 0 0 | 3 0 3 0 0 0 | 3 0 1 0 0 0 | 1 * * *
oxxo ....&#xr ♦ 1 2 2 1 | 2 1 1 2 1 2 | 1 2 0 1 0 1 | * 3 * *
.xx.3.oo.&#x ♦ 0 3 3 0 | 0 0 3 3 3 0 | 0 0 1 3 1 0 | * * 1 *
..xo3..oo&#x ♦ 0 0 3 1 | 0 0 0 0 3 3 | 0 0 0 0 1 3 | * * * 1
o(xo)x3o(oo)o&#xt
(type: pt || ({3} || pt) || para {3})
o(..).3o(..). | 1 * * * ♦ 3 1 0 0 0 0 | 3 3 0 0 0 0 | 1 3 0 0
.(o.).3.(o.). | * 3 * * ♦ 1 0 2 1 0 0 | 2 1 1 2 0 0 | 1 2 1 0
.(.o).3.(.o). | * * 1 * ♦ 0 1 0 0 3 0 | 0 3 0 0 3 0 | 0 3 0 1
.(..)o3.(..)o | * * * 3 ♦ 0 0 0 1 1 1 | 0 1 0 2 2 1 | 0 2 1 1
------------------+---------+-------------+-------------+--------
o(o.).3o(o.).&#x | 1 1 0 0 | 3 * * * * * | 2 1 0 0 0 0 | 1 2 0 0
o(.o).3o(.o).&#x | 1 0 1 0 | * 1 * * * * | 0 3 0 0 0 0 | 0 3 0 0
.(x.). .(..). | 0 2 0 0 | * * 3 * * * | 1 0 1 1 0 0 | 1 1 1 0
.(o.)o3.(o.)o&#x | 0 1 0 1 | * * * 3 * * | 0 1 0 2 0 0 | 0 2 1 0
.(.o)o3.(.o)o&#x | 0 0 1 1 | * * * * 3 * | 0 1 0 0 2 0 | 0 2 0 1
.(..)x .(..). | 0 0 0 2 | * * * * * 3 | 0 0 0 1 1 1 | 0 1 1 1
------------------+---------+-------------+-------------+--------
o(x.). .(..).&#x | 1 2 0 0 | 2 0 1 0 0 0 | 3 * * * * * | 1 1 0 0
o(oo)o o(oo)o&#xt | 1 1 1 1 | 1 1 0 1 1 0 | * 3 * * * * | 0 2 0 0
.(x.).3.(o.). | 0 3 0 0 | 0 0 3 0 0 0 | * * 1 * * * | 1 0 1 0
.(x.)x .(..).&#x | 0 2 0 2 | 0 0 1 2 0 1 | * * * 3 * * | 0 1 1 0
.(.o)x .(..).&#x | 0 0 1 2 | 0 0 0 0 2 1 | * * * * 3 * | 0 1 0 1
.(..)x3.(..)o | 0 0 0 3 | 0 0 0 0 0 3 | * * * * * 1 | 0 0 1 1
------------------+---------+-------------+-------------+--------
o(x.).3o(o.).&#x ♦ 1 3 0 0 | 3 0 3 0 0 0 | 3 0 1 0 0 0 | 1 * * *
o(xo)x .(..).&#xt ♦ 1 2 1 2 | 2 1 1 2 2 1 | 1 2 0 1 1 0 | * 3 * *
.(x.)x3.(o.)o&#x ♦ 0 3 0 3 | 0 0 3 3 0 3 | 0 0 1 3 0 1 | * * 1 *
.(.o)x3.(.o)o&#x ♦ 0 0 1 3 | 0 0 0 0 3 3 | 0 0 0 0 3 1 | * * * 1
©
©
©


