|
Acronym
|
tisdip, K-4.18
|
|
Name
|
triangle - square duoprism,
square - cube wedge,
vertex figure of nit
|
|
|,>,O device
|
line pyramid prism prism = |>||
|
|
|
|
|
|
 © ©  © ©
|
Segmentochoron display /
VRML
|
⭳
|
|
Cross sections
|
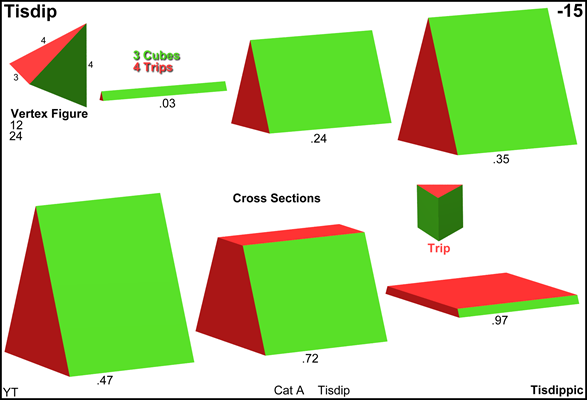 © ©
|
|
Circumradius
|
sqrt(5/6) = 0.912871
|
|
Coordinates
|
-
(1/2, 1/2, 1/2, 1/sqrt(12)) & all changes of sign in first 3 coords.
(cube face)
-
(1/2, 1/2, 0, -1/sqrt(3)) & all changes of sign in 1st & 2nd coord.
(opposite square)
|
|
Volume
|
sqrt(3)/4 = 0.433013
|
|
General of army
|
(is itself convex)
|
|
Colonel of regiment
|
(is itself locally convex)
|
|
Dihedral angles
|
|
|
Face vector
|
12, 24, 19, 7
|
|
Confer
|
- general duoprisms:
-
n,m-dip
2n,m-dip
3,n-dip
4,n-dip
- variations:
-
w x x3o
- ambification:
-
retisdip
- general polytopal classes:
-
Wythoffian polychora
segmentochora
bistratic lace towers
lace simplices
|
External
links
|




|
Incidence matrix according to Dynkin symbol
x3o x4o
. . . . | 12 ♦ 2 2 | 1 4 1 | 2 2
--------+----+-------+--------+----
x . . . | 2 | 12 * | 1 2 0 | 2 1
. . x . | 2 | * 12 | 0 2 1 | 1 2
--------+----+-------+--------+----
x3o . . | 3 | 3 0 | 4 * * | 2 0
x . x . | 4 | 2 2 | * 12 * | 1 1
. . x4o | 4 | 0 4 | * * 3 | 0 2
--------+----+-------+--------+----
x3o x . ♦ 6 | 6 3 | 2 3 0 | 4 *
x . x4o ♦ 8 | 4 8 | 0 4 2 | * 3
x x x3o
. . . . | 12 ♦ 1 1 2 | 1 2 2 1 | 2 1 1
--------+----+--------+---------+------
x . . . | 2 | 6 * * | 1 2 0 0 | 2 1 0
. x . . | 2 | * 6 * | 1 0 2 0 | 2 0 1
. . x . | 2 | * * 12 | 0 1 1 1 | 1 1 1
--------+----+--------+---------+------
x x . . | 4 | 2 2 0 | 3 * * * | 2 0 0
x . x . | 4 | 2 0 2 | * 6 * * | 1 1 0
. x x . | 4 | 0 2 2 | * * 6 * | 1 0 1
. . x3o | 3 | 0 0 3 | * * * 4 | 0 1 1
--------+----+--------+---------+------
x x x . ♦ 8 | 4 4 4 | 2 2 2 0 | 3 * *
x . x3o ♦ 6 | 3 0 6 | 0 3 0 2 | * 2 *
. x x3o ♦ 6 | 0 3 6 | 0 0 3 2 | * * 2
x3o x4/3o
. . . . | 12 ♦ 2 2 | 1 4 1 | 2 2
----------+----+-------+--------+----
x . . . | 2 | 12 * | 1 2 0 | 2 1
. . x . | 2 | * 12 | 0 2 1 | 1 2
----------+----+-------+--------+----
x3o . . | 3 | 3 0 | 4 * * | 2 0
x . x . | 4 | 2 2 | * 12 * | 1 1
. . x4/3o | 4 | 0 4 | * * 3 | 0 2
----------+----+-------+--------+----
x3o x . ♦ 6 | 6 3 | 2 3 0 | 4 *
x . x4/3o ♦ 8 | 4 8 | 0 4 2 | * 3
x3/2o x4o
. . . . | 12 ♦ 2 2 | 1 4 1 | 2 2
----------+----+-------+--------+----
x . . . | 2 | 12 * | 1 2 0 | 2 1
. . x . | 2 | * 12 | 0 2 1 | 1 2
----------+----+-------+--------+----
x3/2o . . | 3 | 3 0 | 4 * * | 2 0
x . x . | 4 | 2 2 | * 12 * | 1 1
. . x4o | 4 | 0 4 | * * 3 | 0 2
----------+----+-------+--------+----
x3/2o x . ♦ 6 | 6 3 | 2 3 0 | 4 *
x . x4o ♦ 8 | 4 8 | 0 4 2 | * 3
x3/2o x4/3o
. . . . | 12 ♦ 2 2 | 1 4 1 | 2 2
------------+----+-------+--------+----
x . . . | 2 | 12 * | 1 2 0 | 2 1
. . x . | 2 | * 12 | 0 2 1 | 1 2
------------+----+-------+--------+----
x3/2o . . | 3 | 3 0 | 4 * * | 2 0
x . x . | 4 | 2 2 | * 12 * | 1 1
. . x4/3o | 4 | 0 4 | * * 3 | 0 2
------------+----+-------+--------+----
x3/2o x . ♦ 6 | 6 3 | 2 3 0 | 4 *
x . x4/3o ♦ 8 | 4 8 | 0 4 2 | * 3
x4o s3s
. . demi( . . ) | 12 ♦ 2 2 | 1 1 4 | 2 2
----------------+----+-------+--------+----
x . demi( . . ) | 2 | 12 * | 1 0 2 | 1 2
. . sefa( s3s ) | 2 | * 12 | 0 1 2 | 2 1
----------------+----+-------+--------+----
x4o demi( . . ) | 4 | 4 0 | 3 * * | 0 2
. . s3s ♦ 3 | 0 3 | * 4 * | 2 0
x . sefa( s3s ) | 4 | 2 2 | * * 12 | 1 1
----------------+----+-------+--------+----
x . s3s ♦ 6 | 3 6 | 0 2 3 | 4 *
x4o sefa( s3s ) ♦ 8 | 8 4 | 2 0 4 | * 3
x x s3s
. . demi( . . ) | 12 ♦ 1 1 2 | 1 1 2 2 | 1 1 2
----------------+----+--------+---------+------
x . demi( . . ) | 2 | 6 * * | 0 1 2 0 | 1 0 2
. x demi( . . ) | 2 | * 6 * | 0 1 0 2 | 0 1 2
. . sefa( s3s ) | 2 | * * 12 | 1 0 1 1 | 1 1 1
----------------+----+--------+---------+------
. . s3s ♦ 3 | 0 0 3 | 4 * * * | 1 1 0
x x demi( . . ) | 4 | 2 2 0 | * 3 * * | 0 0 2
x . sefa( s3s ) | 4 | 2 0 2 | * * 6 * | 1 0 1
. x sefa( s3s ) | 4 | 0 2 2 | * * * 6 | 0 1 1
----------------+----+--------+---------+------
x . s3s ♦ 6 | 3 0 6 | 2 0 3 0 | 2 * *
. x s3s ♦ 6 | 0 3 6 | 2 0 0 3 | * 2 *
x x sefa( s3s ) ♦ 8 | 4 4 4 | 0 2 2 2 | * * 3
xx xx3oo&#x → height = 1
(trip || trip)
o. o.3o. | 6 * ♦ 1 2 1 0 0 | 2 1 1 2 0 0 | 1 2 1 0
.o .o3.o | * 6 ♦ 0 0 1 1 2 | 0 0 1 2 2 1 | 0 2 1 1
------------+-----+-----------+-------------+--------
x. .. .. | 2 0 | 3 * * * * | 2 0 1 0 0 0 | 1 2 0 0
.. x. .. | 2 0 | * 6 * * * | 1 1 0 1 0 0 | 1 1 1 0
oo oo3oo&#x | 1 1 | * * 6 * * | 0 0 1 2 0 0 | 0 2 1 0
.x .. .. | 0 2 | * * * 3 * | 0 0 1 0 2 0 | 0 2 0 1
.. .x .. | 0 2 | * * * * 6 | 0 0 0 1 1 1 | 0 1 1 1
------------+-----+-----------+-------------+--------
x. x. .. | 4 0 | 2 2 0 0 0 | 3 * * * * * | 1 1 0 0
.. x.3o. | 3 0 | 0 3 0 0 0 | * 2 * * * * | 1 0 1 0
xx .. ..&#x | 2 2 | 1 0 2 1 0 | * * 3 * * * | 0 2 0 0
.. xx ..&#x | 2 2 | 0 1 2 0 1 | * * * 6 * * | 0 1 1 0
.x .x .. | 0 4 | 0 0 0 2 2 | * * * * 3 * | 0 1 0 1
.. .x3.o | 0 3 | 0 0 0 0 3 | * * * * * 2 | 0 0 1 1
------------+-----+-----------+-------------+--------
x. x.3o. ♦ 6 0 | 3 6 0 0 0 | 3 2 0 0 0 0 | 1 * * *
xx xx ..&#x ♦ 4 4 | 2 2 4 2 2 | 1 0 2 2 1 0 | * 3 * *
.. xx3oo&#x ♦ 3 3 | 0 3 3 0 3 | 0 1 0 3 0 1 | * * 2 *
.x .x3.o ♦ 0 6 | 0 0 0 3 6 | 0 0 0 0 3 2 | * * * 1
ox xx4oo&#x → height = sqrt(3)/2 = 0.866025
({4} || cube)
o. o.4o. | 4 * ♦ 2 2 0 0 | 1 1 4 0 0 | 2 2 0
.o .o4.o | * 8 ♦ 0 1 1 2 | 0 1 2 2 1 | 2 1 1
------------+-----+---------+-----------+------
.. x. .. | 2 0 | 4 * * * | 1 0 2 0 0 | 1 2 0
oo oo4oo&#x | 1 1 | * 8 * * | 0 1 2 0 0 | 2 1 0
.x .. .. | 0 2 | * * 4 * | 0 1 0 2 0 | 2 0 1
.. .x .. | 0 2 | * * * 8 | 0 0 1 1 1 | 1 1 1
------------+-----+---------+-----------+------
.. x.4o. | 4 0 | 4 0 0 0 | 1 * * * * | 0 2 0
ox .. ..&#x | 1 2 | 0 2 1 0 | * 4 * * * | 2 0 0
.. xx ..&#x | 2 2 | 1 2 0 1 | * * 8 * * | 1 1 0
.x .x .. | 0 4 | 0 0 2 2 | * * * 4 * | 1 0 1
.. .x4.o | 0 4 | 0 0 0 4 | * * * * 2 | 0 1 1
------------+-----+---------+-----------+------
ox xx ..&#x ♦ 2 4 | 1 4 2 2 | 0 2 2 1 0 | 4 * *
.. xx4oo&#x ♦ 4 4 | 4 4 0 4 | 1 0 4 0 1 | * 2 *
.x .x4.o ♦ 0 8 | 0 0 4 8 | 0 0 0 4 2 | * * 1
ox xx xx&#x → height = sqrt(3)/2 = 0.866025
({4} || cube)
o. o. o. | 4 * ♦ 1 1 2 0 0 0 | 1 1 2 2 0 0 0 | 1 1 2 0
.o .o .o | * 8 ♦ 0 0 1 1 1 1 | 0 1 1 1 1 1 1 | 1 1 1 1
------------+-----+-------------+---------------+--------
.. x. .. | 2 0 | 2 * * * * * | 1 0 2 0 0 0 0 | 1 0 2 0
.. .. x. | 2 0 | * 2 * * * * | 1 0 0 2 0 0 0 | 0 1 2 0
oo oo oo&#x | 1 1 | * * 8 * * * | 0 1 1 1 0 0 0 | 1 1 1 0
.x .. .. | 0 2 | * * * 4 * * | 0 1 0 0 1 1 0 | 1 1 0 1
.. .x .. | 0 2 | * * * * 4 * | 0 0 1 0 1 0 1 | 1 0 1 1
.. .. .x | 0 2 | * * * * * 4 | 0 0 0 1 0 1 1 | 0 1 1 1
------------+-----+-------------+---------------+--------
.. x. x. | 4 0 | 2 2 0 0 0 0 | 1 * * * * * * | 0 0 2 0
ox .. ..&#x | 1 2 | 0 0 2 1 0 0 | * 4 * * * * * | 1 1 0 0
.. xx ..&#x | 2 2 | 1 0 2 0 1 0 | * * 4 * * * * | 1 0 1 0
.. .. xx&#x | 2 2 | 0 1 2 0 0 1 | * * * 4 * * * | 0 1 1 0
.x .x .. | 0 4 | 0 0 0 2 2 0 | * * * * 2 * * | 1 0 0 1
.x .. .x | 0 4 | 0 0 0 2 0 2 | * * * * * 2 * | 0 1 0 1
.. .x .x | 0 4 | 0 0 0 0 2 2 | * * * * * * 2 | 0 0 1 1
------------+-----+-------------+---------------+--------
ox xx ..&#x ♦ 2 4 | 1 0 4 2 2 0 | 0 2 2 0 1 0 0 | 2 * * *
ox .. xx&#x ♦ 2 4 | 1 0 4 2 0 2 | 0 2 0 2 0 1 0 | * 2 * *
.. xx xx&#x ♦ 4 4 | 2 2 4 0 2 2 | 1 0 2 2 0 0 1 | * * 2 *
.x .x .x ♦ 0 8 | 0 0 0 4 4 4 | 0 0 0 0 2 2 2 | * * * 1
xxx3ooo oqo&#xt → both heights = 1/sqrt(2) = 0.707107
({3} || pseudo q x3o || {3})
o..3o.. o.. | 3 * * | 2 2 0 0 0 | 1 4 1 0 0 0 | 2 2 0
.o.3.o. .o. | * 6 * | 0 1 2 1 0 | 0 2 1 1 2 0 | 1 2 1
..o3..o ..o | * * 3 | 0 0 0 2 2 | 0 0 1 0 4 1 | 0 2 2
----------------+-------+-----------+-------------+------
x.. ... ... | 2 0 0 | 3 * * * * | 1 2 0 0 0 0 | 2 1 0
oo.3oo. oo.&#x | 1 1 0 | * 6 * * * | 0 2 1 0 0 0 | 1 2 0
.x. ... ... | 0 2 0 | * * 6 * * | 0 1 0 1 1 0 | 1 1 1
.oo3.oo .oo&#x | 0 1 1 | * * * 6 * | 0 0 1 0 2 0 | 0 2 1
..x ... ... | 0 0 2 | * * * * 3 | 0 0 0 0 2 1 | 0 1 2
----------------+-------+-----------+-------------+------
x..3o.. ... | 3 0 0 | 3 0 0 0 0 | 1 * * * * * | 2 0 0
xx. ... ...&#x | 2 2 0 | 1 2 1 0 0 | * 6 * * * * | 1 1 0
... ... oqo&#xt | 1 2 1 | 0 2 0 2 0 | * * 3 * * * | 0 2 0
.x.3.o. ... | 0 3 0 | 0 0 3 0 0 | * * * 2 * * | 1 0 1
.xx ... ...&#x | 0 2 2 | 0 0 1 2 1 | * * * * 6 * | 0 1 1
..x3..o ... | 0 0 3 | 0 0 0 0 3 | * * * * * 1 | 0 0 2
----------------+-------+-----------+-------------+------
xx.3oo. ...&#x ♦ 3 3 0 | 3 3 3 0 0 | 1 3 0 1 0 0 | 2 * *
xxx ... oqo&#xt ♦ 2 4 2 | 1 4 2 4 1 | 0 2 2 0 2 0 | * 3 *
.xx3.oo ...&#x ♦ 0 3 3 | 0 0 3 3 3 | 0 0 0 1 3 1 | * * 2
or
o..3o.. o.. & | 6 * | 2 2 0 | 1 4 1 0 | 2 2
.o.3.o. .o. | * 6 | 0 2 2 | 0 4 1 1 | 2 2
------------------+-----+--------+----------+----
x.. ... ... & | 2 0 | 6 * * | 1 2 0 0 | 2 1
oo.3oo. oo.&#x & | 1 1 | * 12 * | 0 2 1 0 | 1 2
.x. ... ... | 0 2 | * * 6 | 0 2 0 1 | 2 1
------------------+-----+--------+----------+----
x..3o.. ... & | 3 0 | 3 0 0 | 2 * * * | 2 0
xx. ... ...&#x & | 2 2 | 1 2 1 | * 12 * * | 1 1
... ... oqo&#xt | 2 2 | 0 4 0 | * * 3 * | 0 2
.x.3.o. ... | 0 3 | 0 0 3 | * * * 2 | 2 0
------------------+-----+--------+----------+----
xx.3oo. ...&#x & ♦ 3 3 | 3 3 3 | 1 3 0 1 | 4 *
xxx ... oqo&#xt ♦ 4 4 | 2 8 2 | 0 4 2 0 | * 3
xxx xxx&#x → all lacing heights = 1
o.. o.. | 4 * * | 1 1 1 1 0 0 0 0 0 | 1 1 1 1 1 1 0 0 0 0 | 1 1 1 1 0
.o. .o. | * 4 * | 0 0 1 0 1 1 1 0 0 | 0 1 1 0 0 1 1 1 1 0 | 1 0 1 1 1
..o ..o | * * 4 | 0 0 0 0 0 0 1 1 1 | 0 0 0 1 1 1 0 1 1 1 | 0 1 1 1 1
-----------+-------+-------------------+---------------------+----------
x.. ... | 2 0 0 | 2 * * * * * * * * | 1 1 0 1 0 0 0 0 0 0 | 1 1 1 0 0
... x.. | 2 0 0 | * 2 * * * * * * * | 1 0 1 0 1 0 0 0 0 0 | 1 1 0 1 0
oo. oo.&#x | 1 1 0 | * * 4 * * * * * * | 0 1 1 0 0 1 0 0 0 0 | 1 0 1 1 0
o.o o.o&#x | 1 0 0 | * * * 4 * * * * * | 0 0 0 1 1 1 0 0 0 0 | 0 1 1 1 0
.x. ... | 0 2 0 | * * * * 2 * * * * | 0 1 0 0 0 0 1 1 0 0 | 1 0 1 0 1
... .x. | 0 2 0 | * * * * * 2 * * * | 0 0 1 0 0 0 1 0 1 0 | 1 0 0 1 1
.oo .oo&#x | 0 1 1 | * * * * * * 4 * * | 0 0 0 0 0 1 0 1 1 0 | 0 0 1 1 1
..x ... | 0 0 2 | * * * * * * * 2 * | 0 0 0 1 0 0 0 1 0 1 | 0 1 1 0 1
... ..x | 0 0 2 | * * * * * * * * 2 | 0 0 0 0 1 0 0 0 1 1 | 0 1 0 1 1
-----------+-------+-------------------+---------------------+----------
x.. x.. | 4 0 0 | 2 2 0 0 0 0 0 0 0 | 1 * * * * * * * * * | 1 1 0 0 0
xx. ...&#x | 2 2 0 | 1 0 2 0 1 0 0 0 0 | * 2 * * * * * * * * | 1 0 1 0 0
... xx.&#x | 2 2 0 | 0 1 2 0 0 1 0 0 0 | * * 2 * * * * * * * | 1 0 0 1 0
x.x ...&#x | 2 0 2 | 1 0 0 2 0 0 0 1 0 | * * * 2 * * * * * * | 0 1 1 0 0
... x.x&#x | 2 0 2 | 0 1 0 2 0 0 0 0 1 | * * * * 2 * * * * * | 0 1 0 1 0
ooo ooo&#x | 1 1 1 | 0 0 1 1 0 0 1 0 0 | * * * * * 4 * * * * | 0 0 1 1 0
.x. .x. | 0 4 0 | 0 0 0 0 2 2 0 0 0 | * * * * * * 1 * * * | 1 0 0 0 1
.xx ...&#x | 0 2 2 | 0 0 0 0 1 0 2 1 0 | * * * * * * * 2 * * | 0 0 1 0 1
... .xx&#x | 0 2 2 | 0 0 0 0 0 1 2 0 1 | * * * * * * * * 2 * | 0 0 0 1 1
..x ..x | 0 0 4 | 0 0 0 0 0 0 0 2 2 | * * * * * * * * * 1 | 0 1 0 0 1
-----------+-------+-------------------+---------------------+----------
xx. xx.&#x ♦ 4 4 0 | 2 2 4 0 2 2 0 0 0 | 1 2 2 0 0 0 1 0 0 0 | 1 * * * *
x.x x.x&#x ♦ 4 0 4 | 2 2 0 4 0 0 0 2 2 | 1 0 0 2 2 0 0 0 0 1 | * 1 * * *
xxx ...&#x ♦ 2 2 2 | 1 0 2 2 1 0 2 1 0 | 0 1 0 1 0 2 0 1 0 0 | * * 2 * *
... xxx&#x ♦ 2 2 2 | 0 1 2 2 0 1 2 0 1 | 0 0 1 0 1 2 0 0 1 0 | * * * 2 *
.xx .xx&#x ♦ 0 4 4 | 0 0 0 0 2 2 4 2 2 | 0 0 0 0 0 0 1 2 2 1 | * * * * 1
©
©
©


