Acronym	dope, K-4.74
Name	dodecahedron prism
Segmentochoron display
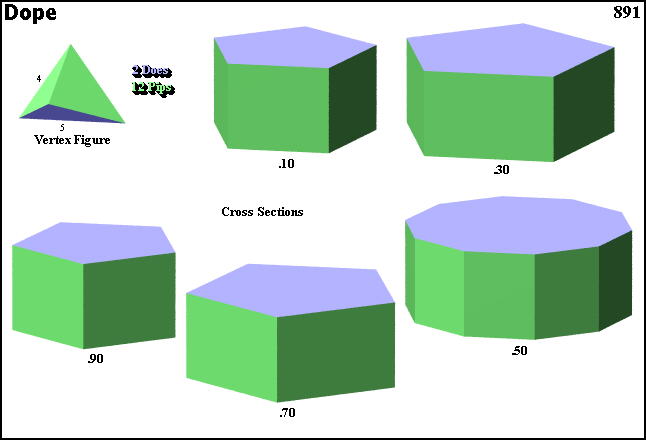
Cross sections	©
Circumradius	sqrt[(11+3 sqrt(5))/8] = 1.487792
Coordinates	(τ/2, τ/2, τ/2, 1/2)   & all permutations in all but last coord., all changes of sign (vertex inscribed f-cube) (τ2/2, 1/2, 0, 1/2)   & even permutations, all changes of sign where τ = (1+sqrt(5))/2
General of army	(is itself convex)
Colonel of regiment	(is itself locally convex – no other uniform polychoral members)
Dual	ite
Dihedral angles	at {4} between pip and pip:   arccos(-1/sqrt(5)) = 116.565051° at {5} between doe and pip:   90°
Face vector	40, 80, 54, 14
Confer	decompositions: ike || dope   general polytopal classes: Wythoffian polychora   segmentochora
External links

As abstract polytope dope is isomorphic to gissiddip, thereby replacing pentagons by pentagrams resp. replacing doe by gissid and pip by stip.

Note that dope can be thought of as the external blend of 20 pens + 30 squascs + 12 pippies + 2 ikadoes. This decomposition is described as the degenerate segmentoteron ox xo3oo5ox&#x.

Incidence matrix according to Dynkin symbol

x o3o5x

. . . . | 40 |  1  3 |  3  3 |  3 1
--------+----+-------+-------+-----
x . . . |  2 | 20  * |  3  0 |  3 0
. . . x |  2 |  * 60 |  1  2 |  2 1
--------+----+-------+-------+-----
x . . x |  4 |  2  2 | 30  * |  2 0
. . o5x |  5 |  0  5 |  * 24 |  1 1
--------+----+-------+-------+-----
x . o5x ♦ 10 |  5 10 |  5  2 | 12 *
. o3o5x ♦ 20 |  0 30 |  0 12 |  * 2

snubbed forms: β2o3o5β

x o3o5/4x

. . .   . | 40 |  1  3 |  3  3 |  3 1
----------+----+-------+-------+-----
x . .   . |  2 | 20  * |  3  0 |  3 0
. . .   x |  2 |  * 60 |  1  2 |  2 1
----------+----+-------+-------+-----
x . .   x |  4 |  2  2 | 30  * |  2 0
. . o5/4x |  5 |  0  5 |  * 24 |  1 1
----------+----+-------+-------+-----
x . o5/4x ♦ 10 |  5 10 |  5  2 | 12 *
. o3o5/4x ♦ 20 |  0 30 |  0 12 |  * 2

x o3/2o5x

. .   . . | 40 |  1  3 |  3  3 |  3 1
----------+----+-------+-------+-----
x .   . . |  2 | 20  * |  3  0 |  3 0
. .   . x |  2 |  * 60 |  1  2 |  2 1
----------+----+-------+-------+-----
x .   . x |  4 |  2  2 | 30  * |  2 0
. .   o5x |  5 |  0  5 |  * 24 |  1 1
----------+----+-------+-------+-----
x .   o5x ♦ 10 |  5 10 |  5  2 | 12 *
. o3/2o5x ♦ 20 |  0 30 |  0 12 |  * 2

x o3/2o5/4x

. .   .   . | 40 |  1  3 |  3  3 |  3 1
------------+----+-------+-------+-----
x .   .   . |  2 | 20  * |  3  0 |  3 0
. .   .   x |  2 |  * 60 |  1  2 |  2 1
------------+----+-------+-------+-----
x .   .   x |  4 |  2  2 | 30  * |  2 0
. .   o5/4x |  5 |  0  5 |  * 24 |  1 1
------------+----+-------+-------+-----
x .   o5/4x ♦ 10 |  5 10 |  5  2 | 12 *
. o3/2o5/4x ♦ 20 |  0 30 |  0 12 |  * 2

oo3oo5xx&#x   → height = 1
(doe || doe)

o.3o.5o.    | 20  * |  3  1  0 |  3  3  0 | 1  3 0
.o3.o5.o    |  * 20 |  0  1  3 |  0  3  3 | 0  3 1
------------+-------+----------+----------+-------
.. .. x.    |  2  0 | 30  *  * |  2  1  0 | 1  2 0
oo3oo5oo&#x |  1  1 |  * 20  * |  0  3  0 | 0  3 0
.. .. .x    |  0  2 |  *  * 30 |  0  1  2 | 0  2 1
------------+-------+----------+----------+-------
.. o.5x.    |  5  0 |  5  0  0 | 12  *  * | 1  1 0
.. .. xx&#x |  2  2 |  1  2  1 |  * 30  * | 0  2 0
.. .o5.x    |  0  5 |  0  0  5 |  *  * 12 | 0  1 1
------------+-------+----------+----------+-------
o.3o.5x.    ♦ 20  0 | 30  0  0 | 12  0  0 | 1  * *
.. oo5xx&#x ♦  5  5 |  5  5  5 |  1  5  1 | * 12 *
.o3.o5.x    ♦  0 20 |  0  0 30 |  0  0 12 | *  * 1