|
Acronym
|
prico
|
|
Name
|
prismatorhombated icositetrachoron,
runcitruncated icositetrachoron
|
|
|
  © ©  ©
(toe first) (sirco first) ©
(toe first) (sirco first)
|
|
Cross section
|
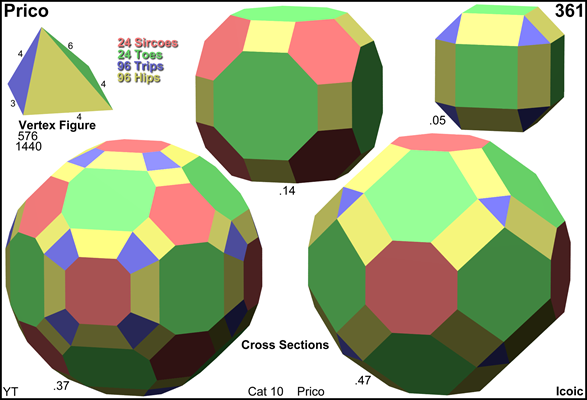 © ©  © ©
|
|
Net
|
 © ©
|
|
Circumradius
|
sqrt[8+3 sqrt(2)] = 3.498949
|
|
Vertex figure
|
 © ©
|
|
Vertex layers
|
| x3x4o3x |
x3x4o .
toe first |
x3x . x
hip first |
x . o3x
trip first |
. x4o3x
sirco first |
| x3x4x . |
w3x . o |
u . q3x |
. u4o3x |
| u3x4x . |
x3u . w |
x . Q3x |
. x4q3x |
| D . o3w |
| Q3x4o . |
w3u . q |
X . w3o |
. u4o3w |
| x3u4x . |
u3x . Y |
w . Y3o |
. x4w3o |
| Z . x3q |
| w3u4o . |
x3X . w |
x . Q3w |
. x4o3Y |
| D . o3Y |
| x3x4w . |
w3D . o |
U . x3o |
. u4x3q |
| X3x . Q |
| w3x4q . |
x3x . A |
u . q3Y |
. x4x3Q |
| . D4x3o |
| x3x4w . |
x3Z . x |
w . Y3q |
. x4x3Q |
| u3w . Y |
Z . x3q |
. D4x3o |
| w3u4o . |
x3w . A |
x . o3A |
. u4x3q |
| x3u4x . |
X3D . o |
X . w3Q |
. x4o3Y |
| Z3x . Q |
| Q3x4o . |
x3x . B |
x . Y3w |
. x4w3o |
| u3x4x . |
u3Z . x |
w . A3o |
. u4o3w |
| D3w . Y |
C . x3o |
| x3x4x . |
Z3u . q |
u . w3Y |
. x4q3x |
x3x4o .
opposite toe |
D3X . w |
U . x3Q |
. u4o3x |
| u3w . A |
| |
x3U . o |
x . x3A |
. x4o3x
opposite sirco |
| Z3x . Y |
x . A3x |
| u3x . B |
Z . w3Q |
|
| C . x3q |
| U3x . x |
X . A3o |
| Z3u . Y |
D . w3Y |
| X3x . A |
| u3Z . Y |
U . o3Y |
| x3X . A |
| x3U . x |
Z . Y3q |
| C . w3o |
| x3u . B |
x . x3A |
| x . A3x |
| U3x . o |
Z . q3Y |
| x3Z . Y |
C . o3w |
| X3D . w |
U . Y3o |
| w3u . A |
| u3Z . q |
D . Y3w |
| Z3u . x |
X . o3A |
| w3D . Y |
| x3x . B |
Z . Q3w |
| C . q3x |
| D3X . o |
x . x3A |
| x3Z . Q |
x . A3x |
| w3x . A |
U . Q3x |
| Z3x . x |
u . Y3w |
| w3u . Y |
| x3x . A |
w . o3A |
| C . o3x |
| D3w . o |
x . w3Y |
| x3X . Q |
| X3x . w |
X . Q3w |
| x3u . Y |
x . A3o |
| u3w . q |
w . q3Y |
| Z . q3x |
| u3x . w |
u . Y3q |
| x3w . o |
U . o3x |
x3x . x
opposite hip |
x . w3Q |
| D . Y3o |
| |
w . o3Y |
| Z . q3x |
| X . o3w |
| x . x3Q |
| D . w3o |
| u . x3q |
x . x3o
opposite trip |
(D=3x, Q=2q, X=wq=x+w=2x+q, Y=x+2q=w+q, Z=3x+q=u+w, U=u+X=4x+q, A=Y+q=x+3q, B=A+x=2x+3q, C=5x+q)
|
Lace city
in approx. ASCII-art
|
 © ©
|
o4x o4u q4x o4u o4x
x4x x4u w4x w4x x4u x4x
x4x x4D w4u w4u x4D x4x
o4x o4Z q4X o4Z o4x
x4u x4D Y4x Y4x x4D x4u
o4u o4Z Q4w o4Z o4u
w4x w4u Y4x Y4x w4u w4x
q4x q4X Q4w Q4w q4X q4x
w4x w4u Y4x Y4x w4u w4x
o4u o4Z Q4w o4Z o4u
x4u x4D Y4x Y4x x4D x4u
o4x o4Z q4X o4Z o4x
x4x x4D w4u w4u x4D x4x
x4x x4u w4x w4x x4u x4x
o4x o4u q4x o4u o4x
|
|
 © ©
|
x3x u3x x3u x3x
x3x x3w u3w # x3X w3u w3x x3x
(X3x)
u3x u3w D3w Z3x x3Z w3D w3u x3u
X3x Z3x x3Z x3X
x3u x3X D3X # u3Z X3D X3x u3x
(Z3u)
w3u Z3u u3Z u3w
x3x x3Z u3Z U3x x3U Z3u Z3x x3x
w3x w3D X3D x3U U3x D3X D3w x3w
x3x x3Z u3Z U3x x3U Z3u Z3x x3x
w3u Z3u u3Z u3w
(Z3u)
x3u x3X D3X # u3Z X3D X3x u3x
X3x Z3x x3Z x3X
u3x u3w D3w Z3x x3Z w3D w3u x3u
(X3x)
x3x x3w u3w # x3X w3u w3x x3x
x3x u3x x3u x3x
|
|
 © ©
|
x3o x3q # o3w q3x o3x
(w3o)
x3o x3Q o3Y Y3o Q3x o3x
(Y3q)
x3q x3Q w3Q # q3Y Q3w Q3x q3x
w3o w3Q A3o o3A Q3w o3w
o3w o3Y w3Y Y3w Y3o w3o
Y3o Y3q A3o o3A q3Y o3Y
q3x q3Y w3Y xA3Ax Y3w Y3q x3q
o3x Q3x Q3w # Y3w xA3Ax xA3Ax # A3o w3Q x3Q x3o
(o3A) (w3Y)
(o3A) (w3Y)
o3x Q3x Q3w # Y3w xA3Ax xA3Ax # A3o w3Q x3Q x3o
q3x q3Y w3Y xA3Ax Y3w Y3q x3q
Y3o Y3q A3o o3A q3Y o3Y
o3w o3Y w3Y Y3w Y3o w3o
w3o w3Q A3o o3A Q3w o3w
x3q x3Q w3Q # q3Y Q3w Q3x q3x
(Y3q)
x3o x3Q o3Y Y3o Q3x o3x
(w3o)
x3o x3q # o3w q3x o3x
|
|
|
General of army
|
(is itself convex)
|
|
Colonel of regiment
|
(is itself locally convex
– uniform polychoral members:
)
|
|
Dihedral angles
|
- at {4} between hip and trip: arccos[-sqrt(8)/3] = 160.528779°
- at {6} between hip and toe: 150°
- at {3} between sirco and trip: 150°
- at {4} between hip and sirco: arccos[-sqrt(2/3)] = 144.735610°
- at {4} between sirco and toe: 135°
|
|
Face vector
|
576, 1440, 1104, 240
|
|
Confer
|
- Grünbaumian relatives:
-
2prico
- uniform relative:
-
gidpith
- segmentochora:
-
toe || girco
- decompositions:
-
tico || gyro prico
srico || prico
- general polytopal classes:
-
Wythoffian polychora
partial Stott expansions
|
External
links
|





|
As abstract polytope prico is isomorphic to paqri,
thereby replacing sirco by querco.
Diminishing the prico by toagircoes at hexadecachoral positions results in the gidpith.
Note that prico can be thought of as the external blend of
1 tico + 24 cubasircoes + 96 tepes
+ 96 thiddips + 24 topes.
This decomposition is described as the degenerate segmentoteron
ox3oo4xx3xx&#x.
–
Alternatively it can be decomposed into
1 srico + 24 coatoes + 96 tricupes
+ 96 triddips + 24 sircopes
according to ox3xx4oo3xx&#x.
Incidence matrix according to Dynkin symbol
x3x4o3x
. . . . | 576 | 1 2 2 | 2 2 1 2 1 | 1 2 1 1
--------+-----+-------------+---------------------+------------
x . . . | 2 | 288 * * | 2 2 0 0 0 | 1 2 1 0
. x . . | 2 | * 576 * | 1 0 1 1 0 | 1 1 0 1
. . . x | 2 | * * 576 | 0 1 0 1 1 | 0 1 1 1
--------+-----+-------------+---------------------+------------
x3x . . | 6 | 3 3 0 | 192 * * * * | 1 1 0 0
x . . x | 4 | 2 0 2 | * 288 * * * | 0 1 1 0
. x4o . | 4 | 0 4 0 | * * 144 * * | 1 0 0 1
. x . x | 4 | 0 2 2 | * * * 288 * | 0 1 0 1
. . o3x | 3 | 0 0 3 | * * * * 192 | 0 0 1 1
--------+-----+-------------+---------------------+------------
x3x4o . ♦ 24 | 12 24 0 | 8 0 6 0 0 | 24 * * *
x3x . x ♦ 12 | 6 6 6 | 2 3 0 3 0 | * 96 * *
x . o3x ♦ 6 | 3 0 6 | 0 3 0 0 2 | * * 96 *
. x4o3x ♦ 24 | 0 24 24 | 0 0 6 12 8 | * * * 24
snubbed forms: β3x4o3x, x3β4o3x, x3x4o3β, s3s4o3x, s3s4o3x (faceting only), β3x4o3β, x3β4o3β, β3β4o3β
x3x4/3o3/2x
. . . . | 576 | 1 2 2 | 2 2 1 2 1 | 1 2 1 1
------------+-----+-------------+---------------------+------------
x . . . | 2 | 288 * * | 2 2 0 0 0 | 1 2 1 0
. x . . | 2 | * 576 * | 1 0 1 1 0 | 1 1 0 1
. . . x | 2 | * * 576 | 0 1 0 1 1 | 0 1 1 1
------------+-----+-------------+---------------------+------------
x3x . . | 6 | 3 3 0 | 192 * * * * | 1 1 0 0
x . . x | 4 | 2 0 2 | * 288 * * * | 0 1 1 0
. x4/3o . | 4 | 0 4 0 | * * 144 * * | 1 0 0 1
. x . x | 4 | 0 2 2 | * * * 288 * | 0 1 0 1
. . o3/2x | 3 | 0 0 3 | * * * * 192 | 0 0 1 1
------------+-----+-------------+---------------------+------------
x3x4/3o . ♦ 24 | 12 24 0 | 8 0 6 0 0 | 24 * * *
x3x . x ♦ 12 | 6 6 6 | 2 3 0 3 0 | * 96 * *
x . o3/2x ♦ 6 | 3 0 6 | 0 3 0 0 2 | * * 96 *
. x4/3o3/2x ♦ 24 | 0 24 24 | 0 0 6 12 8 | * * * 24
s3s4x3x
demi( . . . . ) | 576 | 1 1 2 1 | 1 1 1 2 2 1 | 1 1 1 2
----------------+-----+-----------------+-----------------------+------------
demi( . . x . ) | 2 | 288 * * * | 1 0 1 1 0 0 | 1 0 1 1
demi( . . . x ) | 2 | * 288 * * | 1 0 0 0 2 1 | 0 1 1 2
sefa( s3s . . ) | 2 | * * 576 * | 0 1 0 1 1 0 | 1 1 0 1
sefa( . s4x . ) | 2 | * * * 288 | 0 0 1 1 0 1 | 1 0 1 1
----------------+-----+-----------------+-----------------------+------------
demi( . . x3x ) | 6 | 3 3 0 0 | 96 * * * * * | 0 0 1 1
s3s . . ♦ 3 | 0 0 3 0 | * 192 * * * * | 1 1 0 0
. s4x . ♦ 4 | 2 0 0 2 | * * 144 * * * | 1 0 1 0
sefa( s3s4x . ) | 4 | 1 0 2 1 | * * * 288 * * | 1 0 0 1
sefa( s3s 2 x ) | 4 | 0 2 2 0 | * * * * 288 * | 0 1 0 1
sefa( . s4x3x ) | 6 | 0 3 0 3 | * * * * * 96 | 0 0 1 1
----------------+-----+-----------------+-----------------------+------------
s3s4x . ♦ 24 | 12 0 24 12 | 0 8 6 12 0 0 | 24 * * *
s3s 2 x ♦ 6 | 0 3 6 0 | 0 2 0 0 3 0 | * 96 * *
. s4x3x ♦ 24 | 12 12 0 12 | 4 0 6 0 0 4 | * * 24 *
sefa( s3s4x3x ) ♦ 12 | 3 6 6 3 | 1 0 0 3 3 1 | * * * 96
starting figure: x3x4x3x
((wx3xx3xx4ox))&#zx → height = 0
(tegum sum of (w,x,x,x)-tico and gidpith)
o.3o.3o.4o. | 192 * | 1 2 2 0 0 0 0 | 2 1 2 2 1 0 0 0 0 0 | 1 1 2 1 0 0
.o3.o3.o4.o | * 384 | 0 0 1 1 1 1 1 | 0 0 1 1 1 1 1 1 1 1 | 0 1 1 1 1 1
--------------------+---------+----------------------------+----------------------------------+-----------------
.. x. .. .. | 2 0 | 96 * * * * * * | 2 0 2 0 0 0 0 0 0 0 | 1 0 2 1 0 0
.. .. x. .. | 2 0 | * 192 * * * * * | 1 1 0 1 0 0 0 0 0 0 | 1 1 1 0 0 0
oo3oo3oo4oo &#x | 1 1 | * * 384 * * * * | 0 0 1 1 1 0 0 0 0 0 | 0 1 1 1 0 0
.x .. .. .. | 0 2 | * * * 192 * * * | 0 0 0 0 0 1 1 1 0 0 | 0 1 0 0 1 1
.. .x .. .. | 0 2 | * * * * 192 * * | 0 0 1 0 0 1 0 0 1 1 | 0 0 1 1 1 1
.. .. .x .. | 0 2 | * * * * * 192 * | 0 0 0 1 0 0 1 0 1 0 | 0 1 1 0 1 0
.. .. .. .x | 0 2 | * * * * * * 192 | 0 0 0 0 1 0 0 1 0 1 | 0 1 0 1 0 1
--------------------+---------+----------------------------+----------------------------------+-----------------
.. x.3x. .. | 6 0 | 3 3 0 0 0 0 0 | 64 * * * * * * * * * | 1 0 1 0 0 0
.. .. x.4o. | 4 0 | 0 4 0 0 0 0 0 | * 48 * * * * * * * * | 1 1 0 0 0 0
.. xx .. .. &#x | 2 2 | 1 0 2 0 1 0 0 | * * 192 * * * * * * * | 0 0 1 1 0 0
.. .. xx .. &#x | 2 2 | 0 1 2 0 0 1 0 | * * * 192 * * * * * * | 0 1 1 0 0 0
.. .. .. ox &#x | 1 2 | 0 0 2 0 0 0 1 | * * * * 192 * * * * * | 0 1 0 1 0 0
.x3.x .. .. | 0 6 | 0 0 0 3 3 0 0 | * * * * * 64 * * * * | 0 0 0 0 1 1
.x .. .x .. | 0 4 | 0 0 0 2 0 2 0 | * * * * * * 96 * * * | 0 1 0 0 1 0
.x .. .. .x | 0 4 | 0 0 0 2 0 0 2 | * * * * * * * 96 * * | 0 1 0 0 0 1
.. .x3.x .. | 0 6 | 0 0 0 0 3 3 0 | * * * * * * * * 64 * | 0 0 1 0 1 0
.. .x .. .x | 0 4 | 0 0 0 0 2 0 2 | * * * * * * * * * 96 | 0 0 0 1 0 1
--------------------+---------+----------------------------+----------------------------------+-----------------
.. x.3x.4o. ♦ 24 0 | 12 24 0 0 0 0 0 | 8 6 0 0 0 0 0 0 0 0 | 8 * * * * *
((wx .. xx4ox))&#zx ♦ 8 16 | 0 8 16 8 0 8 8 | 0 2 0 8 8 0 4 4 0 0 | * 24 * * * *
.. xx3xx .. &#x ♦ 6 6 | 3 3 6 0 3 3 0 | 1 0 3 3 0 0 0 0 1 0 | * * 64 * * *
.. xx .. ox &#x ♦ 2 4 | 1 0 4 0 2 0 2 | 0 0 2 0 2 0 0 0 0 1 | * * * 96 * *
.x3.x3.x .. ♦ 0 24 | 0 0 0 12 12 12 0 | 0 0 0 0 0 4 6 0 4 0 | * * * * 16 *
.x3.x .. .x ♦ 0 12 | 0 0 0 6 6 0 6 | 0 0 0 0 0 2 0 3 0 3 | * * * * * 32
((wxx3xxx3xwx *b3xxw))&#zx → all heights = 0
(tegum sum of 3 mutually gyrated (w,x,x)-ticoes)
o..3o..3o.. *b3o.. | 192 * * | 1 1 1 1 1 0 0 0 0 0 0 0 | 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 | 1 1 1 1 1 0 0 0
.o.3.o.3.o. *b3.o. | * 192 * | 0 0 0 1 0 1 1 1 1 0 0 0 | 0 0 0 1 1 0 0 1 1 1 1 1 1 0 0 0 | 0 1 0 1 1 1 1 0
..o3..o3..o *b3..o | * * 192 | 0 0 0 0 1 0 0 0 1 1 1 1 | 0 0 0 0 0 1 1 1 0 0 0 1 1 1 1 1 | 0 0 1 1 1 0 1 1
---------------------------+-------------+----------------------------------------+--------------------------------------------------+---------------------
... x.. ... ... | 2 0 0 | 96 * * * * * * * * * * * | 1 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 | 1 1 1 0 1 0 0 0
... ... x.. ... | 2 0 0 | * 96 * * * * * * * * * * | 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 | 1 0 1 1 0 0 0 0
... ... ... x.. | 2 0 0 | * * 96 * * * * * * * * * | 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 | 1 1 0 1 0 0 0 0
oo.3oo.3oo. *b3oo. &#x | 1 1 0 | * * * 192 * * * * * * * * | 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 | 0 1 0 1 1 0 0 0
o.o3o.o3o.o3*b3o.o &#x | 1 0 1 | * * * * 192 * * * * * * * | 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 | 0 0 1 1 1 0 0 0
.x. ... ... ... | 0 2 0 | * * * * * 96 * * * * * * | 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 | 0 0 0 1 0 1 1 0
... .x. ... ... | 0 2 0 | * * * * * * 96 * * * * * | 0 0 0 1 0 0 0 0 1 0 1 0 1 0 0 0 | 0 1 0 0 1 1 1 0
... ... ... .x. | 0 2 0 | * * * * * * * 96 * * * * | 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 | 0 1 0 1 0 1 0 0
.oo3.oo3.oo *b3.oo &#x | 0 1 1 | * * * * * * * * 192 * * * | 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 | 0 0 0 1 1 0 1 0
..x ... ... ... | 0 0 2 | * * * * * * * * * 96 * * | 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 | 0 0 0 1 0 0 1 1
... ..x ... ... | 0 0 2 | * * * * * * * * * * 96 * | 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 1 | 0 0 1 0 1 0 1 1
... ... ..x ... | 0 0 2 | * * * * * * * * * * * 96 | 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 | 0 0 1 1 0 0 0 1
---------------------------+-------------+----------------------------------------+--------------------------------------------------+---------------------
... x..3x.. ... | 6 0 0 | 3 3 0 0 0 0 0 0 0 0 0 0 | 32 * * * * * * * * * * * * * * * | 1 0 1 0 0 0 0 0
... x.. ... *b3x.. | 6 0 0 | 3 0 3 0 0 0 0 0 0 0 0 0 | * 32 * * * * * * * * * * * * * * | 1 1 0 0 0 0 0 0
... ... x.. x.. | 4 0 0 | 0 2 2 0 0 0 0 0 0 0 0 0 | * * 48 * * * * * * * * * * * * * | 1 0 0 1 0 0 0 0
... xx. ... ... &#x | 2 2 0 | 1 0 0 2 0 0 1 0 0 0 0 0 | * * * 96 * * * * * * * * * * * * | 0 1 0 0 1 0 0 0
... ... ... xx. &#x | 2 2 0 | 0 0 1 2 0 0 0 1 0 0 0 0 | * * * * 96 * * * * * * * * * * * | 0 1 0 1 0 0 0 0
... x.x ... ... &#x | 2 0 2 | 1 0 0 0 2 0 0 0 0 0 1 0 | * * * * * 96 * * * * * * * * * * | 0 0 1 0 1 0 0 0
... ... x.x ... &#x | 2 0 2 | 0 1 0 0 2 0 0 0 0 0 0 1 | * * * * * * 96 * * * * * * * * * | 0 0 1 1 0 0 0 0
ooo3ooo3ooo *b3ooo &#x | 1 1 1 | 0 0 0 1 1 0 0 0 1 0 0 0 | * * * * * * * 192 * * * * * * * * | 0 0 0 1 1 0 0 0
.x.3.x. ... ... | 0 6 0 | 0 0 0 0 0 3 3 0 0 0 0 0 | * * * * * * * * 32 * * * * * * * | 0 0 0 0 0 1 1 0
.x. ... ... .x. | 0 4 0 | 0 0 0 0 0 2 0 2 0 0 0 0 | * * * * * * * * * 48 * * * * * * | 0 0 0 1 0 1 0 0
... .x. ... *b3.x. | 0 6 0 | 0 0 0 0 0 0 3 3 0 0 0 0 | * * * * * * * * * * 32 * * * * * | 0 1 0 0 0 1 0 0
.xx ... ... ... &#x | 0 2 2 | 0 0 0 0 0 1 0 0 2 1 0 0 | * * * * * * * * * * * 96 * * * * | 0 0 0 1 0 0 1 0
... .xx ... ... &#x | 0 2 2 | 0 0 0 0 0 0 1 0 2 0 1 0 | * * * * * * * * * * * * 96 * * * | 0 0 0 0 1 0 1 0
..x3..x ... ... | 0 0 6 | 0 0 0 0 0 0 0 0 0 3 3 0 | * * * * * * * * * * * * * 32 * * | 0 0 0 0 0 0 1 1
..x ... ..x ... | 0 0 4 | 0 0 0 0 0 0 0 0 0 2 0 2 | * * * * * * * * * * * * * * 48 * | 0 0 0 1 0 0 0 1
... ..x3..x ... | 0 0 6 | 0 0 0 0 0 0 0 0 0 0 3 3 | * * * * * * * * * * * * * * * 32 | 0 0 1 0 0 0 0 1
---------------------------+-------------+----------------------------------------+--------------------------------------------------+---------------------
... x..3x.. *b3x.. ♦ 24 0 0 | 12 12 12 0 0 0 0 0 0 0 0 0 | 4 4 6 0 0 0 0 0 0 0 0 0 0 0 0 0 | 8 * * * * * * *
... xx. ... *b3xx. &#x ♦ 6 6 0 | 3 0 3 6 0 0 3 3 0 0 0 0 | 0 1 0 3 3 0 0 0 0 0 1 0 0 0 0 0 | * 32 * * * * * *
... x.x3x.x ... &#x ♦ 6 0 6 | 3 3 0 0 6 0 0 0 0 0 3 3 | 1 0 0 0 0 3 3 0 0 0 0 0 0 0 0 1 | * * 32 * * * * *
((wxx ... xwx xxw))&#zx ♦ 8 8 8 | 0 4 4 8 8 4 0 4 8 4 0 4 | 0 0 2 0 4 0 4 8 0 2 0 4 0 0 2 0 | * * * 24 * * * *
... xxx ... ... &#x ♦ 2 2 2 | 1 0 0 2 2 0 1 0 2 0 1 0 | 0 0 0 1 0 1 0 2 0 0 0 0 1 0 0 0 | * * * * 96 * * *
.x.3.x. ... *b3.x. ♦ 0 24 0 | 0 0 0 0 0 12 12 12 0 0 0 0 | 0 0 0 0 0 0 0 0 4 6 4 0 0 0 0 0 | * * * * * 8 * *
.xx3.xx ... ... &#x ♦ 0 6 6 | 0 0 0 0 0 3 3 0 6 3 3 0 | 0 0 0 0 0 0 0 0 1 0 0 3 3 1 0 0 | * * * * * * 32 *
..x3..x3..x ... ♦ 0 0 24 | 0 0 0 0 0 0 0 0 0 12 12 12 | 0 0 0 0 0 0 0 0 0 0 0 0 0 4 6 4 | * * * * * * * 8
((oqQ3xxx3qoo4xux))&#zxt → heights = 0, Q=2q = 2.828427
(tegum sum of (x,q,x)-grit, (q,x,u)-prit, and (Q,x,x)-prit)
o..3o..3o..4o.. | 192 * * | 2 1 2 0 0 0 0 | 1 2 1 2 2 0 0 0 0 0 | 1 1 1 2 0 0
.o.3.o.3.o.4.o. | * 192 * | 0 0 2 2 1 0 0 | 0 0 1 2 2 1 2 0 0 0 | 0 1 1 2 1 0
..o3..o3..o4..o | * * 192 | 0 0 0 0 1 2 2 | 0 0 0 0 2 0 2 1 2 1 | 0 0 1 2 1 1
-------------------------+-------------+----------------------------+----------------------------------+-----------------
... x.. ... ... | 2 0 0 | 192 * * * * * * | 1 1 0 1 0 0 0 0 0 0 | 1 1 0 1 0 0
... ... ... x.. | 2 0 0 | * 96 * * * * * | 0 2 0 0 2 0 0 0 0 0 | 1 0 1 2 0 0
oo.3oo.3oo.4oo. &#x | 1 1 0 | * * 384 * * * * | 0 0 1 1 1 0 0 0 0 0 | 0 1 1 1 0 0
... .x. ... ... | 0 2 0 | * * * 192 * * * | 0 0 0 1 0 1 1 0 0 0 | 0 1 0 1 1 0
.oo3.oo3.oo4.oo &#x | 0 1 1 | * * * * 192 * * | 0 0 0 0 2 0 2 0 0 0 | 0 0 1 2 1 0
... ..x ... ... | 0 0 2 | * * * * * 192 * | 0 0 0 0 0 0 1 1 1 0 | 0 0 0 1 1 1
... ... ... ..x | 0 0 2 | * * * * * * 192 | 0 0 0 0 1 0 0 0 1 1 | 0 0 1 1 0 1
-------------------------+-------------+----------------------------+----------------------------------+-----------------
o..3x.. ... ... | 3 0 0 | 3 0 0 0 0 0 0 | 64 * * * * * * * * * | 1 1 0 0 0 0
... x.. ... x.. | 4 0 0 | 2 2 0 0 0 0 0 | * 96 * * * * * * * * | 1 0 0 1 0 0
((oq. ... qo. ...))&#zx | 2 2 0 | 0 0 4 0 0 0 0 | * * 96 * * * * * * * | 0 1 1 0 0 0
... xx. ... ... &#x | 2 2 0 | 1 0 2 1 0 0 0 | * * * 192 * * * * * * | 0 1 0 1 0 0
... ... ... xux &#xt | 2 2 2 | 0 1 2 0 2 0 1 | * * * * 192 * * * * * | 0 0 1 1 0 0
... .x.3.o. ... | 0 3 0 | 0 0 0 3 0 0 0 | * * * * * 64 * * * * | 0 1 0 0 1 0
... .xx ... ... &#x | 0 2 2 | 0 0 0 1 2 1 0 | * * * * * * 192 * * * | 0 0 0 1 1 0
... ..x3..o ... | 0 0 3 | 0 0 0 0 0 3 0 | * * * * * * * 64 * * | 0 0 0 0 1 1
... ..x ... ..x | 0 0 4 | 0 0 0 0 0 2 2 | * * * * * * * * 96 * | 0 0 0 1 0 1
... ... ..o4..x | 0 0 4 | 0 0 0 0 0 0 4 | * * * * * * * * * 48 | 0 0 1 0 0 1
-------------------------+-------------+----------------------------+----------------------------------+-----------------
o..3x.. ... x.. ♦ 6 0 0 | 6 3 0 0 0 0 0 | 2 3 0 0 0 0 0 0 0 0 | 32 * * * * *
((oq.3xx.3qo. ...))&#zx ♦ 12 12 0 | 12 0 24 12 0 0 0 | 4 0 6 12 0 4 0 0 0 0 | * 16 * * * *
((oqQ ... qoo4xux))&#zxt ♦ 8 8 8 | 0 4 16 0 8 0 8 | 0 0 4 0 8 0 0 0 0 2 | * * 24 * * *
... xxx ... xux &#xt ♦ 4 4 4 | 2 2 4 2 4 2 2 | 0 1 0 2 2 0 2 0 1 0 | * * * 96 * *
... .xx3.oo ... &#x ♦ 0 3 3 | 0 0 0 3 3 3 0 | 0 0 0 0 0 1 3 1 0 0 | * * * * 64 *
... ..x3..o4..x ♦ 0 0 24 | 0 0 0 0 0 24 24 | 0 0 0 0 0 0 0 8 12 6 | * * * * * 8

©
© (toe first) (sirco first)
©
©
©
©






