|
Acronym
|
triddip, K-4.10
|
|
Name
|
triangle-triangle duoprism,
triangle - trip wedge,
vertex figure of dot,
Delone cell of lattice A2×A2,
equatorial cross-section of trig-first rix
|
|
|
|
|
|
 © ©  © ©
|
Segmentochoron display /
VRML
|
⭳
|
|
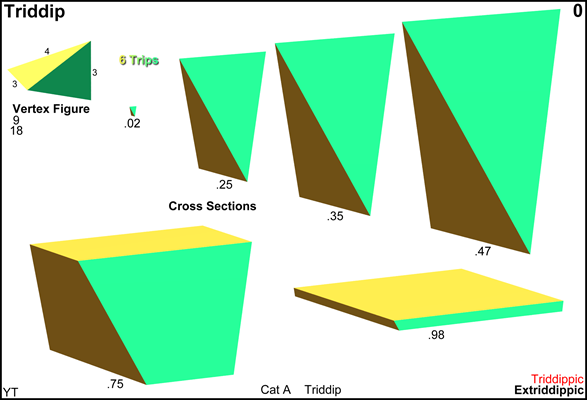
Cross sections
|
 © ©
|
|
Circumradius
|
sqrt(2/3) = 0.816497
|
|
Inradius
|
1/sqrt(12) = 0.288675
|
|
Vertex figure
|
 © ©
|
|
Coordinates
|
(εn, εm)/sqrt(3) n,m ∈ {0,1,2}
where ε = exp(2πi/3) and R4=C2
|
|
Volume
|
3/16 = 0.1875
|
|
Surface
|
sqrt(27)/2 = 2.598076
|
|
General of army
|
(is itself convex)
|
|
Colonel of regiment
|
(is itself locally convex)
|
|
Dihedral angles
|
|
|
Dual
|
triddit
|
|
Face vector
|
9, 18, 15, 6
|
|
Confer
|
- general duoprisms:
-
3,n-dip
n,n-dip
n,m-dip
- ambification:
-
retdip
- general polytopal classes:
-
Wythoffian polychora
noble polytopes
segmentochora
lace simplices
- analogs:
-
simplex duoprism Sn×Sn
|
External
links
|




|
Incidence matrix according to Dynkin symbol
x3o x3o
. . . . | 9 ♦ 2 2 | 1 4 1 | 2 2
--------+---+-----+-------+----
x . . . | 2 | 9 * | 1 2 0 | 2 1
. . x . | 2 | * 9 | 0 2 1 | 1 2
--------+---+-----+-------+----
x3o . . | 3 | 3 0 | 3 * * | 2 0
x . x . | 4 | 2 2 | * 9 * | 1 1
. . x3o | 3 | 0 3 | * * 3 | 0 2
--------+---+-----+-------+----
x3o x . ♦ 6 | 6 3 | 2 3 0 | 3 *
x . x3o ♦ 6 | 3 6 | 0 3 2 | * 3
or
. . . . | 9 ♦ 4 | 2 4 | 4
-----------+---+----+-----+--
x . . . & | 2 | 18 | 1 2 | 3
-----------+---+----+-----+--
x3o . . & | 3 | 3 | 6 * | 2
x . x . | 4 | 4 | * 9 | 2
-----------+---+----+-----+--
x3o x . & ♦ 6 | 9 | 2 3 | 6
s3s x3o
demi( . . ) . . | 9 ♦ 2 2 | 1 1 4 | 2 2
----------------+---+-----+-------+----
demi( . . ) x . | 2 | 9 * | 1 0 2 | 1 2
sefa( s3s ) . . | 2 | * 9 | 0 1 2 | 2 1
----------------+---+-----+-------+----
demi( . . ) x3o | 3 | 3 0 | 3 * * | 0 2
s3s . . | 3 | 0 3 | * 3 * | 2 0
sefa( s3s ) x . | 4 | 2 2 | * * 9 | 1 1
----------------+---+-----+-------+----
s3s x . ♦ 6 | 3 6 | 0 2 3 | 3 *
sefa( s3s ) x3o ♦ 6 | 6 3 | 2 0 3 | * 3
s3s2x3o
demi( . . . . ) | 9 ♦ 2 2 | 1 1 4 | 2 2
----------------+---+-----+-------+----
demi( . . x . ) | 2 | 9 * | 1 0 2 | 1 2
sefa( s3s . . ) | 2 | * 9 | 0 1 2 | 2 1
----------------+---+-----+-------+----
demi( . . x3o ) | 3 | 3 0 | 3 * * | 0 2
s3s . . | 3 | 0 3 | * 3 * | 2 0
sefa( s3s2x . ) | 4 | 2 2 | * * 9 | 1 1
----------------+---+-----+-------+----
s3s2x . ♦ 6 | 3 6 | 0 2 3 | 3 *
sefa( s3s2x3o ) ♦ 6 | 6 3 | 2 0 3 | * 3
starting figure: x3x x3o
ox xx3oo&#x → height = sqrt(3)/2 = 0.866025
({3} || trip)
o. o.3o. | 3 * ♦ 2 2 0 0 | 1 1 4 0 0 | 2 2 0
.o .o3.o | * 6 ♦ 0 1 1 2 | 0 1 2 2 1 | 2 1 1
------------+-----+---------+-----------+------
.. x. .. | 2 0 | 3 * * * | 1 0 2 0 0 | 1 2 0
oo oo3oo&#x | 1 1 | * 6 * * | 0 1 2 0 0 | 2 1 0
.x .. .. | 0 2 | * * 3 * | 0 1 0 2 0 | 2 0 1
.. .x .. | 0 2 | * * * 6 | 0 0 1 1 1 | 1 1 1
------------+-----+---------+-----------+------
.. x.3o. | 3 0 | 3 0 0 0 | 1 * * * * | 0 2 0
ox .. ..&#x | 1 2 | 0 2 1 0 | * 3 * * * | 2 0 0
.. xx ..&#x | 2 2 | 1 2 0 1 | * * 6 * * | 1 1 0
.x .x .. | 0 4 | 0 0 2 2 | * * * 3 * | 1 0 1
.. .x3.o | 0 3 | 0 0 0 3 | * * * * 2 | 0 1 1
------------+-----+---------+-----------+------
ox xx ..&#x ♦ 2 4 | 1 4 2 2 | 0 2 2 1 0 | 3 * *
.. xx3oo&#x ♦ 3 3 | 3 3 0 3 | 1 0 3 0 1 | * 2 *
.x .x3.o ♦ 0 6 | 0 0 3 6 | 0 0 0 3 2 | * * 1
xxoo xoox&#xr → all heights = sqrt(3)/2 = 0.866025
({4} || pseudo q-laced (line || perp line) || pt)
o(..). o(..). | 4 * * * ♦ 1 1 1 1 0 0 0 0 | 1 1 1 1 1 1 0 0 | 1 1 1 1
.(o.). .(o.). | * 2 * * ♦ 0 0 2 0 1 1 0 0 | 0 2 1 0 0 2 1 0 | 1 0 2 1
.(.o). .(.o). | * * 2 * ♦ 0 0 0 2 0 0 1 1 | 0 0 0 1 2 2 0 1 | 0 1 1 2
.(..)o .(..)o | * * * 1 ♦ 0 0 0 0 0 2 0 2 | 0 0 0 0 0 4 1 1 | 0 0 2 2
------------------+---------+-----------------+-----------------+--------
x(..). .(..). | 2 0 0 0 | 2 * * * * * * * | 1 1 0 1 0 0 0 0 | 1 1 1 0
.(..). x(..). | 2 0 0 0 | * 2 * * * * * * | 1 0 1 0 1 0 0 0 | 1 1 0 1
o(o.). o(o.).&#x | 1 1 0 0 | * * 4 * * * * * | 0 1 1 0 0 1 0 0 | 1 0 1 1
o(.o). o(.o).&#x | 1 0 1 0 | * * * 4 * * * * | 0 0 0 1 1 1 0 0 | 0 1 1 1
.(x.). .(..). | 0 2 0 0 | * * * * 1 * * * | 0 2 0 0 0 0 1 0 | 1 0 2 0
.(o.)o .(o.)o&#x | 0 1 0 1 | * * * * * 2 * * | 0 0 0 0 0 2 1 0 | 0 0 2 1
.(..). .(.x). | 0 0 2 0 | * * * * * * 1 * | 0 0 0 0 2 0 0 1 | 0 1 0 2
.(.o)o .(.o)o&#x | 0 0 1 1 | * * * * * * * 2 | 0 0 0 0 0 2 0 1 | 0 0 1 2
------------------+---------+-----------------+-----------------+--------
x(..). x(..). | 4 0 0 0 | 2 2 0 0 0 0 0 0 | 1 * * * * * * * | 1 1 0 0
x(x.). .(..).&#x | 2 2 0 0 | 1 0 2 0 1 0 0 0 | * 2 * * * * * * | 1 0 1 0
.(..). x(o.).&#x | 2 1 0 0 | 0 1 2 0 0 0 0 0 | * * 2 * * * * * | 1 0 0 1
x(.o). .(..).&#x | 2 0 1 0 | 1 0 0 2 0 0 0 0 | * * * 2 * * * * | 0 1 1 0
.(..). x(.x).&#x | 2 0 2 0 | 0 1 0 2 0 0 1 0 | * * * * 2 * * * | 0 1 0 1
o(oo)o o(oo)o&#xt | 1 1 1 1 | 0 0 1 1 0 1 0 1 | * * * * * 4 * * | 0 0 1 1
.(x.)o .(..).&#x | 0 2 0 1 | 0 0 0 0 1 2 0 0 | * * * * * * 1 * | 0 0 2 0
.(..). .(.x)o&#x | 0 0 2 1 | 0 0 0 0 0 0 1 2 | * * * * * * * 1 | 0 0 0 2
------------------+---------+-----------------+-----------------+--------
x(x.). x(o.).&#x ♦ 4 2 0 0 | 2 2 4 0 1 0 0 0 | 1 2 2 0 0 0 0 0 | 1 * * *
x(.o). x(.x).&#x ♦ 4 0 2 0 | 2 2 0 4 0 0 1 0 | 1 0 0 2 2 0 0 0 | * 1 * *
x(xo)o .(..).&#xt ♦ 2 2 1 1 | 1 0 2 2 1 2 0 1 | 0 1 0 1 0 2 1 0 | * * 2 *
.(..). x(ox)o&#xt ♦ 2 1 2 1 | 0 1 2 2 0 1 1 2 | 0 0 1 0 1 2 0 1 | * * * 2
or
o(..). o(..). | 4 * * ♦ 2 2 0 0 | 1 2 2 1 0 | 2 2
.(o.). .(o.). & | * 4 * ♦ 0 2 1 1 | 0 2 1 2 1 | 1 3
.(..)o .(..)o | * * 1 ♦ 0 0 0 4 | 0 0 0 4 2 | 0 4
--------------------+-------+---------+-----------+----
x(..). .(..). & | 2 0 0 | 4 * * * | 1 1 1 0 0 | 2 1
o(o.). o(o.).&#x & | 1 1 0 | * 8 * * | 0 1 1 1 0 | 1 2
.(x.). .(..). & | 0 2 0 | * * 2 * | 0 2 0 0 1 | 1 2
.(o.)o .(o.)o&#x & | 0 1 1 | * * * 4 | 0 0 0 2 1 | 0 3
--------------------+-------+---------+-----------+----
x(..). x(..). | 4 0 0 | 4 0 0 0 | 1 * * * * | 2 0
x(x.). .(..).&#x & | 2 2 0 | 1 2 1 0 | * 4 * * * | 1 1
.(..). x(o.).&#x & | 2 1 0 | 1 2 0 0 | * * 4 * * | 1 1
o(oo)o o(oo)o&#xt | 1 2 1 | 0 2 0 2 | * * * 4 * | 0 2
.(x.)o .(..).&#x & | 0 2 1 | 0 0 1 2 | * * * * 2 | 0 2
--------------------+-------+---------+-----------+----
x(x.). x(o.).&#x & ♦ 4 2 0 | 4 4 1 0 | 1 2 2 0 0 | 2 *
x(xo)o .(..).&#xr & ♦ 2 3 1 | 1 4 1 3 | 0 1 1 2 1 | * 4
©
©
©
©


