Acronym	cogart (old: gocart)
Name	celligreatorhombated triacontiditeron, (great cellirhombated triacontiditeron), stericantitruncated pentacross
Field of sections	©
Circumradius	sqrt[33+12 sqrt(2)]/2 = 3.534493
Vertex figure	©   ©
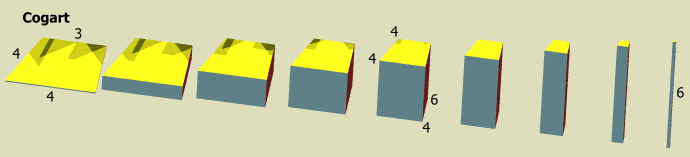Coordinates	((1+3 sqrt(2))/2, (1+2 sqrt(2))/2, (1+sqrt(2))/2, 1/2, 1/2)   & all permutations, all changes of sign
General of army	(is itself convex)
Colonel of regiment	(is itself locally convex – uniform polyteral members: by cells: gidpith grip prit shiddip sichado sircope soccope tope sibcotdin 10 32 0 80 10 0 40 0 cogart 0 32 10 80 0 40 0 80 & others)
Face vector	1920, 5760, 5920, 2320, 242
Confer	related segmentotera: gidpithip   general polytopal classes: Wythoffian polytera   partial Stott expansions
External links

As abstract polytope cogart is isomorphic to quicgrat, thereby replacing sirco by querco, resp. sircope by quercope and prit by paqrit.

Incidence matrix according to Dynkin symbol

x3x3x3o4x

. . . . . | 1920 |   1   1    2    2 |   1   2   2   2   2   1   2   1 |   2   2   1   2   1   1   2   1  1 |  1  2  1  1  1
----------+------+-------------------+---------------------------------+------------------------------------+---------------
x . . . . |    2 | 960   *    *    * |   1   2   2   0   0   0   0   0 |   2   2   1   2   1   0   0   0  0 |  1  2  1  1  0
. x . . . |    2 |   * 960    *    * |   1   0   0   2   2   0   0   0 |   2   2   0   0   0   1   2   1  0 |  1  2  1  0  1
. . x . . |    2 |   *   * 1920    * |   0   1   0   1   0   1   1   0 |   1   0   1   1   0   1   1   0  1 |  1  1  0  1  1
. . . . x |    2 |   *   *    * 1920 |   0   0   1   0   1   0   1   1 |   0   1   0   1   1   0   1   1  1 |  0  1  1  1  1
----------+------+-------------------+---------------------------------+------------------------------------+---------------
x3x . . . |    6 |   3   3    0    0 | 320   *   *   *   *   *   *   * |   2   2   0   0   0   0   0   0  0 |  1  2  1  0  0
x . x . . |    4 |   2   0    2    0 |   * 960   *   *   *   *   *   * |   1   0   1   1   0   0   0   0  0 |  1  1  0  1  0
x . . . x |    4 |   2   0    0    2 |   *   * 960   *   *   *   *   * |   0   1   0   1   1   0   0   0  0 |  0  1  1  1  0
. x3x . . |    6 |   0   3    3    0 |   *   *   * 640   *   *   *   * |   1   0   0   0   0   1   1   0  0 |  1  1  0  0  1
. x . . x |    4 |   0   2    0    2 |   *   *   *   * 960   *   *   * |   0   1   0   0   0   0   1   1  0 |  0  1  1  0  1
. . x3o . |    3 |   0   0    3    0 |   *   *   *   *   * 640   *   * |   0   0   1   0   0   1   0   0  1 |  1  0  0  1  1
. . x . x |    4 |   0   0    2    2 |   *   *   *   *   *   * 960   * |   0   0   0   1   0   0   1   0  1 |  0  1  0  1  1
. . . o4x |    4 |   0   0    0    4 |   *   *   *   *   *   *   * 480 |   0   0   0   0   1   0   0   1  1 |  0  0  1  1  1
----------+------+-------------------+---------------------------------+------------------------------------+---------------
x3x3x . . ♦   24 |  12  12   12    0 |   4   6   0   4   0   0   0   0 | 160   *   *   *   *   *   *   *  * |  1  1  0  0  0
x3x . . x ♦   12 |   6   6    0    6 |   2   0   3   0   3   0   0   0 |   * 320   *   *   *   *   *   *  * |  0  1  1  0  0
x . x3o . ♦    6 |   3   0    6    0 |   0   3   0   0   0   2   0   0 |   *   * 320   *   *   *   *   *  * |  1  0  0  1  0
x . x . x ♦    8 |   4   0    4    4 |   0   2   2   0   0   0   2   0 |   *   *   * 480   *   *   *   *  * |  0  1  0  1  0
x . . o4x ♦    8 |   4   0    0    8 |   0   0   4   0   0   0   0   2 |   *   *   *   * 240   *   *   *  * |  0  0  1  1  0
. x3x3o . ♦   12 |   0   6   12    0 |   0   0   0   4   0   4   0   0 |   *   *   *   *   * 160   *   *  * |  1  0  0  0  1
. x3x . x ♦   12 |   0   6    6    6 |   0   0   0   2   3   0   3   0 |   *   *   *   *   *   * 320   *  * |  0  1  0  0  1
. x . o4x ♦    8 |   0   4    0    8 |   0   0   0   0   4   0   0   2 |   *   *   *   *   *   *   * 240  * |  0  0  1  0  1
. . x3o4x ♦   24 |   0   0   24   24 |   0   0   0   0   0   8  12   6 |   *   *   *   *   *   *   *   * 80 |  0  0  0  1  1
----------+------+-------------------+---------------------------------+------------------------------------+---------------
x3x3x3o . ♦   60 |  30  30   60    0 |  10  30   0  20   0  20   0   0 |   5   0  10   0   0   5   0   0  0 | 32  *  *  *  *
x3x3x . x ♦   48 |  24  24   24   24 |   8  12  12   8  12   0  12   0 |   2   4   0   6   0   0   4   0  0 |  * 80  *  *  *
x3x . o4x ♦   24 |  12  12    0   24 |   4   0  12   0  12   0   0   6 |   0   4   0   0   3   0   0   3  0 |  *  * 80  *  *
x . x3o4x ♦   48 |  24   0   48   48 |   0  24  24   0   0  16  24  12 |   0   0   8  12   6   0   0   0  2 |  *  *  * 40  *
. x3x3o4x ♦  192 |   0  96  192  192 |   0   0   0  64  96  64  96  48 |   0   0   0   0   0  16  32  24  8 |  *  *  *  * 10

snubbed forms: x3x3x3o4s