Acronym ike   (alt.: snit)
TOCID symbol I, sO, sTT
Name icosahedron,
snub tetrahedron,
snub tetratetrahedron,
snub triangle antiprism,
hydrohedron,
gyroelongated pentagonal bipyramid,
vertex figure of ex
  
 © ©    ©
Circumradius sqrt[(5+sqrt(5))/8] = 0.951057
Edge radius (1+sqrt(5))/4 = 0.809017
Inradius sqrt[(7+3 sqrt(5))/24] = 0.755761
Vertex figure [35] = x5o
Snub derivation
Vertex layers
LayerSymmetrySubsymmetries
 o3o5oo3o .o . o. o5o
1x3o5ox3o .
{3} first		x . o
edge first		. o5o
vertex first
2o3f .o . f. x5o
vertex figure
3f3o .f . x. o5x
4o3x .
opposite {3}		o . f. o5o
opposite vertex
5 x . o
opposite edge		 
Lace city
in approx. ASCII-art 
 o   o 
   f   
x     x
   f   
 o   o
Coordinates (f/2, 1/2, 0)   & even permutations, all changes of sign
where f = (1+sqrt(5))/2
General of army (is itself convex)
Colonel of regiment (is itself locally convex – other uniform polyhedral member: gad – other edge facetings)
Dual doe
Dihedral angles
  • between {3} and {3}:   arccos(-sqrt(5)/3) = 138.189685°
Face vector 12, 30, 20
Confer
Grünbaumian relatives:
2ike   cid   ike+2gad   2ike+gad   ike+3gad   3ike+gad   3ike+3gad   4ike+gad   5ike+gad   2ike+4gad   4ike+2gad  
related Johnson solids:
peppy   gyepip   mibdi   teddi   pedpy   snadow   snisquap  
facetings:
peppy   gyepip   pap   mibdi   teddi   scuffi   bitdi   ike-6-2   toif  
stellations:
gike   ki   e   se   ditti  
blends:
2 pap blend  
compounds:
siddo   sne   pedisna-verf (biform)  
variations:
cube-dim-doe   alternated toe   general pyritohedral ike  
ambification:
id  
general polytopal classes:
Wythoffian polyhedra   Catalan polyhedra   deltahedra   regular   noble polytopes   expanded kaleido-facetings   subsymmetrical diminishings  
External
links 		hedrondude   wikipedia   polytopewiki   WikiChoron   mathworld   Polyedergarten   quickfur   nan ma
©

As abstract polytope ike is isomorphic to gike, thereby replacing vertex figure pentagons by corresponding pentagrams.

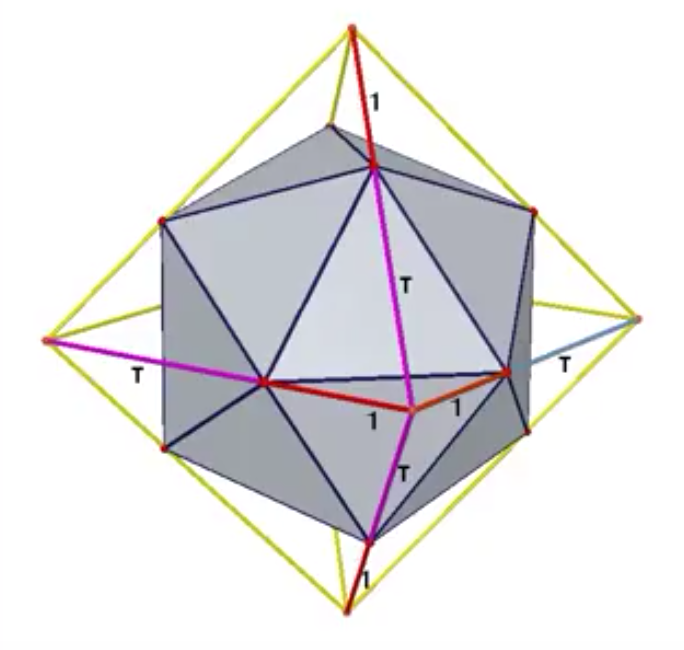
A q-ike can be face-inscribed into an F-oct. Its edges then are to be dissected in the ratio f:x, cf. the pic at the right.

The number of ways to color the icosahedron with different colors per face is 20!/60 = 40 548 366 802 944 000. – This is because the color group is the permutation group of 20 elements and has size 20!, while the order of the pure rotational icosahedral group is 60. (The reflectional icosahedral group would have twice as many, i.e. 120 elements.)

The (direct) snub derivational process features 2 operations, first the mere alternated faceting, here wrt. a to be alternated vertices of toe as its starting figure, which then would result in qQo oqQ Qoq&#zh (where Q = 2q), a pyritohedrally gyrated ike variant, and a secondary edge rescaling to all unit sizes only.

→
s before s'

The quartersnub derivation of s3s4s':
Independent of the application order the subsequent snubbing processes will result within the same shape again. This is why this quartersnub really is well-defined: i.e. the ike well can be obtained from girco. (Esp. it is fully independently of a later-on to be applied resizement towards all-unit edges.)

The first stellation of ike happens to be the dual of sidtid, i.e. stai. 

     x3x4x
  
     s3s4x
↓   s' before s   ↓   s' after s
→
s after s' 
     x3x4s'
  
     s3s4s'
©

Incidence matrix according to Dynkin symbol

x3o5o

. . . | 12 |  5 |  5
------+----+----+---
x . . |  2 | 30 |  2
------+----+----+---
x3o . |  3 |  3 | 20

snubbed forms: β3o5o


x3/2o5o

.   . . | 12 |  5 |  5
--------+----+----+---
x   . . |  2 | 30 |  2
--------+----+----+---
x3/2o . |  3 |  3 | 20


o5/4o3x

.   . . | 12 |  5 |  5
--------+----+----+---
.   . x |  2 | 30 |  2
--------+----+----+---
.   o3x |  3 |  3 | 20


o5/4o3/2x

.   .   . | 12 |  5 |  5
----------+----+----+---
.   .   x |  2 | 30 |  2
----------+----+----+---
.   o3/2x |  3 |  3 | 20


in pyritohedral symmetry:

12 |  4 1 | 2  3
---+------+-----
 2 | 24 * | 1  1  per cube-vertex
 2 |  * 6 | 0  2
---+------+-----
 3 |  3 0 | 8  *
 3 |  2 1 | * 12


s3s3s

demi( . . . ) | 12 | 1  2  2 | 1 1  3
--------------+----+---------+-------
      s 2 s   |  2 | 6  *  * | 0 0  2
sefa( s3s . ) |  2 | * 12  * | 1 0  1
sefa( . s3s ) |  2 | *  * 12 | 0 1  1
--------------+----+---------+-------
      s3s .   ♦  3 | 0  3  0 | 4 *  *
      . s3s   ♦  3 | 0  0  3 | * 4  *
sefa( s3s3s ) |  3 | 1  1  1 | * * 12

or
demi( . . . )                   | 12 | 1  4 | 2  3
--------------------------------+----+------+-----
      s 2 s                     |  2 | 6  * | 0  2
sefa( s3s . )  &  sefa( . s3s ) |  2 | * 24 | 1  1
--------------------------------+----+------+-----
      s3s .    &        . s3s   ♦  3 | 0  3 | 8  *
sefa( s3s3s )                   |  3 | 1  2 | * 12

starting figure: x3x3x


s3s4o

demi( . . . ) | 12 | 1  4 | 2  3
--------------+----+------+-----
      . s4o   |  2 | 6  * | 0  2
sefa( s3s . ) |  2 | * 24 | 1  1
--------------+----+------+-----
      s3s .   ♦  3 | 0  3 | 8  *
sefa( s3s4o ) |  3 | 1  2 | * 12

starting figure: x3x4o


s3s4/3o

demi( . .   . ) | 12 | 1  4 | 2  3
----------------+----+------+-----
      . s4/3o   |  2 | 6  * | 0  2
sefa( s3s   . ) |  2 | * 24 | 1  1
----------------+----+------+-----
      s3s   .   ♦  3 | 0  3 | 8  *
sefa( s3s4/3o ) |  3 | 1  2 | * 12

starting figure: x3x4/3o


oxoo5ooxo&#xt   → outer heights = sqrt((5-sqrt(5))/10) = 0.525731,
                  inner height  = sqrt((5+sqrt(5))/10) = 0.850651
(pt || pseudo {5} || dual pseudo {5} || pt)

o...5o...    | 1 * * * | 5 0  0 0 0 | 5 0 0 0
.o..5.o..    | * 5 * * | 1 2  2 0 0 | 2 2 1 0
..o.5..o.    | * * 5 * | 0 0  2 2 1 | 0 1 2 2
...o5...o    | * * * 1 | 0 0  0 0 5 | 0 0 0 5
-------------+---------+------------+--------
oo..5oo..&#x | 1 1 0 0 | 5 *  * * * | 2 0 0 0
.x.. ....    | 0 2 0 0 | * 5  * * * | 1 1 0 0
.oo. .oo.&#x | 0 1 1 0 | * * 10 * * | 0 1 1 0
.... ..x.    | 0 0 2 0 | * *  * 5 * | 0 0 1 1
..oo5..oo&#x | 0 0 1 1 | * *  * * 5 | 0 0 0 2
-------------+---------+------------+--------
ox.. ....&#x | 1 2 0 0 | 2 1  0 0 0 | 5 * * *
.xo. ....&#x | 0 2 1 0 | 0 1  2 0 0 | * 5 * *
.... .ox.&#x | 0 1 2 0 | 0 0  2 1 0 | * * 5 *
.... ..xo&#x | 0 0 2 1 | 0 0  0 1 2 | * * * 5

or
o...5o...    & | 2  * |  5  0  0 |  5  0
.o..5.o..    & | * 10 |  1  2  2 |  2  3
---------------+------+----------+------
oo..5oo..&#x & | 1  1 | 10  *  * |  2  0
.x.. ....    & | 0  2 |  * 10  * |  1  1
.oo. .oo.&#x   | 0  2 |  *  * 10 |  0  2
---------------+------+----------+------
ox.. ....&#x & | 1  2 |  2  1  0 | 10  *
.xo. ....&#x & | 0  3 |  0  1  2 |  * 10


xofo3ofox&#xt   → outer heights = 1/sqrt(3) = 0.577350
                  inner height = sqrt[(3-sqrt(5))/6] = 0.356822
({3} || pseudo dual f-{3} || pseudo f-{3} || dual {3})

o...3o...     | 3 * * * | 2 2 1 0 0 0 0 | 1 2 2 0 0 0
.o..3.o..     | * 3 * * | 0 2 0 2 1 0 0 | 0 1 2 2 0 0
..o.3..o.     | * * 3 * | 0 0 1 2 0 2 0 | 0 0 2 2 1 0
...o3...o     | * * * 3 | 0 0 0 0 1 2 2 | 0 0 0 2 2 1
--------------+---------+---------------+------------
x... ....     | 2 0 0 0 | 3 * * * * * * | 1 1 0 0 0 0
oo..3oo..&#x  | 1 1 0 0 | * 6 * * * * * | 0 1 1 0 0 0
o.o.3o.o.&#x  | 1 0 1 0 | * * 3 * * * * | 0 0 2 0 0 0
.oo.3.oo.&#x  | 0 1 1 0 | * * * 6 * * * | 0 0 1 1 0 0
.o.o3.o.o&#x  | 0 1 0 1 | * * * * 3 * * | 0 0 0 2 0 0
..oo3..oo&#x  | 0 0 1 1 | * * * * * 6 * | 0 0 0 1 1 0
.... ...x     | 0 0 0 2 | * * * * * * 3 | 0 0 0 0 1 1
--------------+---------+---------------+------------
x...3o...     | 3 0 0 0 | 3 0 0 0 0 0 0 | 1 * * * * *
xo.. ....&#x  | 2 1 0 0 | 1 2 0 0 0 0 0 | * 3 * * * *
ooo.3ooo.&#xt | 1 1 1 0 | 0 1 1 1 0 0 0 | * * 6 * * *
.ooo3.ooo&#xt | 0 1 1 1 | 0 0 0 1 1 1 0 | * * * 6 * *
.... ..ox&#x  | 0 0 1 2 | 0 0 0 0 0 2 1 | * * * * 3 *
...o3...x     | 0 0 0 3 | 0 0 0 0 0 0 3 | * * * * * 1

or
o...3o...      & | 6 * | 2  2 1 0 | 1 2  2
.o..3.o..      & | * 6 | 0  2 1 2 | 0 1  4
-----------------+-----+----------+-------
x... ....      & | 2 0 | 6  * * * | 1 1  0
oo..3oo..&#x   & | 1 1 | * 12 * * | 0 1  1
o.o.3o.o.&#x   & | 1 1 | *  * 6 * | 0 0  2
.oo.3.oo.&#x     | 0 2 | *  * * 6 | 0 0  2
-----------------+-----+----------+-------
x...3o...      & | 3 0 | 3  0 0 0 | 2 *  *
xo.. ....&#x   & | 2 1 | 1  2 0 0 | * 6  *
ooo.3ooo.&#xt  & | 1 2 | 0  1 1 1 | * * 12


xofox ofxfo&#xt   → outer heights = (sqrt(5)-1)/4 = 0.309017
                    inner heights = 1/2
(line || pseudo ortho f-line || pseudo (f,x)-{4} || pseudo ortho f-line || line)

o.... o....     | 2 * * * * | 1 2 2 0 0 0 0 0 0 0 | 2 2 1 0 0 0 0
.o... .o...     | * 2 * * * | 0 2 0 2 1 0 0 0 0 0 | 1 2 0 2 0 0 0
..o.. ..o..     | * * 4 * * | 0 0 1 1 0 1 1 1 0 0 | 0 1 1 1 1 1 0
...o. ...o.     | * * * 2 * | 0 0 0 0 1 0 2 0 2 0 | 0 0 0 2 2 0 1
....o ....o     | * * * * 2 | 0 0 0 0 0 0 0 2 2 1 | 0 0 0 0 2 1 2
----------------+-----------+---------------------+--------------
x.... .....     | 2 0 0 0 0 | 1 * * * * * * * * * | 2 0 0 0 0 0 0
oo... oo...&#x  | 1 1 0 0 0 | * 4 * * * * * * * * | 1 1 0 0 0 0 0
o.o.. o.o..&#x  | 1 0 1 0 0 | * * 4 * * * * * * * | 0 1 1 0 0 0 0
.oo.. .oo..&#x  | 0 1 1 0 0 | * * * 4 * * * * * * | 0 1 0 1 0 0 0
.o.o. .o.o.&#x  | 0 1 0 1 0 | * * * * 2 * * * * * | 0 0 0 2 0 0 0
..... ..x..     | 0 0 2 0 0 | * * * * * 2 * * * * | 0 0 1 0 0 1 0
..oo. ..oo.&#x  | 0 0 1 1 0 | * * * * * * 4 * * * | 0 0 0 1 1 0 0
..o.o ..o.o&#x  | 0 0 1 0 1 | * * * * * * * 4 * * | 0 0 0 0 1 1 0
...oo ...oo&#x  | 0 0 0 1 1 | * * * * * * * * 4 * | 0 0 0 0 1 0 1
....x .....     | 0 0 0 0 2 | * * * * * * * * * 1 | 0 0 0 0 0 0 2
----------------+-----------+---------------------+--------------
xo... .....&#x  | 2 1 0 0 0 | 1 2 0 0 0 0 0 0 0 0 | 2 * * * * * *
ooo.. ooo..&#xt | 1 1 1 0 0 | 0 1 1 1 0 0 0 0 0 0 | * 4 * * * * *
..... o.x..&#x  | 1 0 2 0 0 | 0 0 2 0 0 1 0 0 0 0 | * * 2 * * * *
.ooo. .ooo.&#xt | 0 1 1 1 0 | 0 0 0 1 1 0 1 0 0 0 | * * * 4 * * *
..ooo ..ooo&#xt | 0 0 1 1 1 | 0 0 0 0 0 0 1 1 1 0 | * * * * 4 * *
..... ..x.o&#x  | 0 0 2 0 1 | 0 0 0 0 0 1 0 2 0 0 | * * * * * 2 *
...ox .....&#x  | 0 0 0 1 2 | 0 0 0 0 0 0 0 0 2 1 | * * * * * * 2

or
o.... o....      & | 4 * * | 1 2 2 0 0 0 | 2 2 1 0
.o... .o...      & | * 4 * | 0 2 0 2 1 0 | 1 2 0 2
..o.. ..o..        | * * 4 | 0 0 2 2 0 1 | 0 2 2 1
-------------------+-------+-------------+--------
x.... .....      & | 2 0 0 | 2 * * * * * | 2 0 0 0
oo... oo...&#x   & | 1 1 0 | * 8 * * * * | 1 1 0 0
o.o.. o.o..&#x   & | 1 0 1 | * * 8 * * * | 0 1 1 0
.oo.. .oo..&#x   & | 0 1 1 | * * * 8 * * | 0 1 0 1
.o.o. .o.o.&#x     | 0 2 0 | * * * * 2 * | 0 0 0 2
..... ..x..        | 0 0 2 | * * * * * 2 | 0 0 2 0
-------------------+-------+-------------+--------
xo... .....&#x   & | 2 1 0 | 1 2 0 0 0 0 | 4 * * *
ooo.. ooo..&#xt  & | 1 1 1 | 0 1 1 1 0 0 | * 8 * *
..... o.x..&#x   & | 1 0 2 | 0 0 2 0 0 1 | * * 4 *
.ooo. .ooo.&#xt    | 0 2 1 | 0 0 0 2 1 0 | * * * 4


fxo ofx xof&#zx   → all heights = 0
(tegum sum of 3 pairwise perpendicular (x,f)-{4}'s)

o.. o.. o..    | 4 * * | 1 2 2 0 0 0 | 2 1 2 0
.o. .o. .o.    | * 4 * | 0 2 0 1 2 0 | 1 0 2 2
..o ..o ..o    | * * 4 | 0 0 2 0 2 1 | 0 2 2 1
---------------+-------+-------------+--------
... ... x..    | 2 0 0 | 2 * * * * * | 2 0 0 0
oo. oo. oo.&#x | 1 1 0 | * 8 * * * * | 1 0 1 0
o.o o.o o.o&#x | 1 0 1 | * * 8 * * * | 0 1 1 0
.x. ... ...    | 0 2 0 | * * * 2 * * | 0 0 0 2
.oo .oo .oo&#x | 0 1 1 | * * * * 8 * | 0 0 1 1
... ..x ...    | 0 0 2 | * * * * * 2 | 0 2 0 0
---------------+-------+-------------+--------
... ... xo.&#x | 2 1 0 | 1 2 0 0 0 0 | 4 * * *
... o.x ...&#x | 1 0 2 | 0 0 2 0 0 1 | * 4 * *
ooo ooo ooo&#x | 1 1 1 | 0 1 1 0 1 0 | * * 8 *
.xo ... ...&#x | 0 2 1 | 0 0 0 1 2 0 | * * * 4

or
o.. o.. o..     & | 12 | 1  4 |  3 2
------------------+----+------+-----
... ... x..     & |  2 | 6  * |  2 0
oo. oo. oo.&#x  & |  2 | * 24 |  1 1
------------------+----+------+-----
... ... xo.&#x  & |  3 | 1  2 | 12 *
ooo ooo ooo&#x    |  3 | 0  3 |  * 8

© 2004-2024
top of page