Acronym	griddip, K-4.150
Name	great-rhombicosidodecahedron prism
Segmentochoron display / VRML	⭳
Cross sections	©
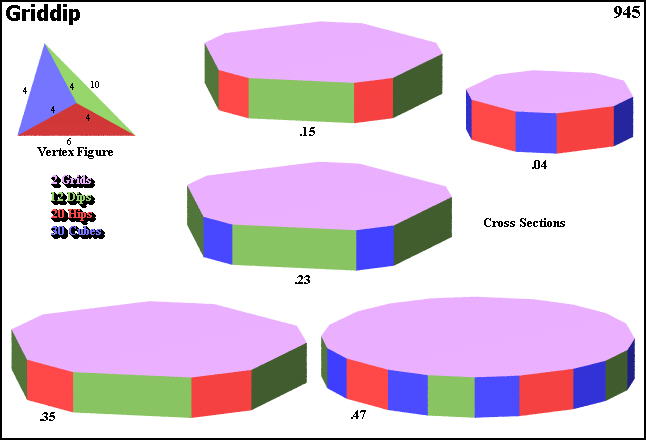Circumradius	sqrt[8+3 sqrt(5)] = 3.835128
Dihedral angles	at {4} between cube and hip:   arccos(-(1+sqrt(5))/sqrt(12)) = 159.094843° at {4} between cube and dip:   arccos(-sqrt[(5+sqrt(5))/10]) = 148.282526° at {4} between dip and hip:   arccos(-sqrt[(5+2 sqrt(5))/15]) = 142.622632° at {4} between cube and grid:   90° at {10} between dip and grid:   90° at {6} between grid and hip:   90°
Face vector	240, 480, 304, 64
Confer	general polytopal classes: Wythoffian polychora   segmentochora
External links

As abstract polytope griddip is isomorphic to gaquatiddip, thereby replacing decagons by decagrams, resp. replacing grid by gaquatid and dip by stiddip.

Incidence matrix according to Dynkin symbol

x x3x5x

. . . . | 240 |   1   1   1   1 |  1  1  1  1  1  1 |  1  1  1 1
--------+-----+-----------------+-------------------+-----------
x . . . |   2 | 120   *   *   * |  1  1  1  0  0  0 |  1  1  1 0
. x . . |   2 |   * 120   *   * |  1  0  0  1  1  0 |  1  1  0 1
. . x . |   2 |   *   * 120   * |  0  1  0  1  0  1 |  1  0  1 1
. . . x |   2 |   *   *   * 120 |  0  0  1  0  1  1 |  0  1  1 1
--------+-----+-----------------+-------------------+-----------
x x . . |   4 |   2   2   0   0 | 60  *  *  *  *  * |  1  1  0 0
x . x . |   4 |   2   0   2   0 |  * 60  *  *  *  * |  1  0  1 0
x . . x |   4 |   2   0   0   2 |  *  * 60  *  *  * |  0  1  1 0
. x3x . |   6 |   0   3   3   0 |  *  *  * 40  *  * |  1  0  0 1
. x . x |   4 |   0   2   0   2 |  *  *  *  * 60  * |  0  1  0 1
. . x5x |  10 |   0   0   5   5 |  *  *  *  *  * 24 |  0  0  1 1
--------+-----+-----------------+-------------------+-----------
x x3x . ♦  12 |   6   6   6   0 |  3  3  0  2  0  0 | 20  *  * *
x x . x ♦   8 |   4   4   0   4 |  2  0  2  0  2  0 |  * 30  * *
x . x5x ♦  20 |  10   0  10  10 |  0  5  5  0  0  2 |  *  * 12 *
. x3x5x ♦ 120 |   0  60  60  60 |  0  0  0 20 30 12 |  *  *  * 2

snubbed forms: x s3s5s, s2s3s5s

xx3xx5xx&#x   → height = 1
(grid || grid)


o.3o.5o.    | 120   * |  1  1  1   1  0  0  0 |  1  1  1  1  1  1  0  0  0 | 1  1  1  1 0
.o3.o5.o    |   * 120 |  0  0  0   1  1  1  1 |  0  0  0  1  1  1  1  1  1 | 0  1  1  1 1
------------+---------+-----------------------+----------------------------+-------------
x. .. ..    |   2   0 | 60  *  *   *  *  *  * |  1  1  0  1  0  0  0  0  0 | 1  1  1  0 0
.. x. ..    |   2   0 |  * 60  *   *  *  *  * |  1  0  1  0  1  0  0  0  0 | 1  1  0  1 0
.. .. x.    |   2   0 |  *  * 60   *  *  *  * |  0  1  1  0  0  1  0  0  0 | 1  0  1  1 0
oo3oo5oo&#x |   1   1 |  *  *  * 120  *  *  * |  0  0  0  1  1  1  0  0  0 | 0  1  1  1 0
.x .. ..    |   0   2 |  *  *  *   * 60  *  * |  0  0  0  1  0  0  1  1  0 | 0  1  1  0 1
.. .x ..    |   0   2 |  *  *  *   *  * 60  * |  0  0  0  0  1  0  1  0  1 | 0  1  0  1 1
.. .. .x    |   0   2 |  *  *  *   *  *  * 60 |  0  0  0  0  0  1  0  1  1 | 0  0  1  1 1
------------+---------+-----------------------+----------------------------+-------------
x.3x. ..    |   6   0 |  3  3  0   0  0  0  0 | 20  *  *  *  *  *  *  *  * | 1  1  0  0 0
x. .. x.    |   4   0 |  2  0  2   0  0  0  0 |  * 30  *  *  *  *  *  *  * | 1  0  1  0 0
.. x.5x.    |  10   0 |  0  5  5   0  0  0  0 |  *  * 12  *  *  *  *  *  * | 1  0  0  1 0
xx .. ..&#x |   2   2 |  1  0  0   2  1  0  0 |  *  *  * 60  *  *  *  *  * | 0  1  1  0 0
.. xx ..&#x |   2   2 |  0  1  0   2  0  1  0 |  *  *  *  * 60  *  *  *  * | 0  1  0  1 0
.. .. xx&#x |   2   2 |  0  0  1   2  0  0  1 |  *  *  *  *  * 60  *  *  * | 0  0  1  1 0
.x3.x ..    |   0   6 |  0  0  0   0  3  3  0 |  *  *  *  *  *  * 20  *  * | 0  1  0  0 1
.x .. .x    |   0   4 |  0  0  0   0  2  0  2 |  *  *  *  *  *  *  * 30  * | 0  0  1  0 1
.. .x5.x    |   0  10 |  0  0  0   0  0  5  5 |  *  *  *  *  *  *  *  * 12 | 0  0  0  1 1
------------+---------+-----------------------+----------------------------+-------------
x.3x.5x.    ♦ 120   0 | 60 60 60   0  0  0  0 | 20 30 12  0  0  0  0  0  0 | 1  *  *  * *
xx3xx ..&#x ♦   6   6 |  3  3  0   6  3  3  0 |  1  0  0  3  3  0  1  0  0 | * 20  *  * *
xx .. xx&#x ♦   4   4 |  2  0  2   4  2  0  2 |  0  1  0  2  0  2  0  1  0 | *  * 30  * *
.. xx5xx&#x ♦  10  10 |  0  5  5  10  0  5  5 |  0  0  1  0  5  5  0  0  1 | *  *  * 12 *
.x3.x5.x    ♦   0 120 |  0  0  0   0 60 60 60 |  0  0  0  0  0  0 20 30 12 | *  *  *  * 1