rico

Acronym rico

Name rectified icosatetrachoron,
cantellated hexadecachoron,
hexadecachoron-derived Gévay polychoron,
equatorial cross-section of ico-first sart

Cross sections

©

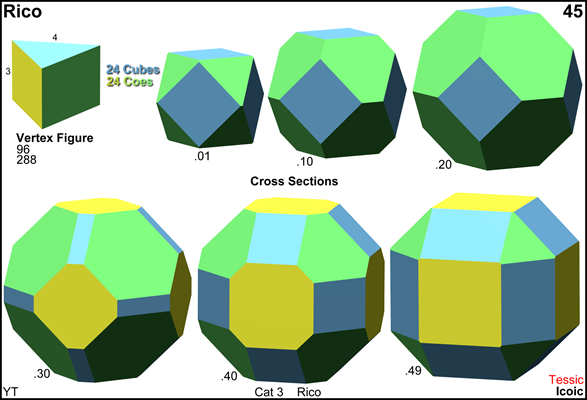Circumradius sqrt(3) = 1.732051

Inradius
wrt. cube 3/2 = 1.5

Inradius
wrt. co sqrt(2) = 1.414214

Vertex figure

©

Vertex layers

Layer	Symmetry	Subsymmetries
	`o3o4o3o`	`o3o4o .`	`o3o . o`	`o . o3o`	`. o4o3o`
1	`o3x4o3o`	`o3x4o .` co first	`o3x . o` {3} first	`o . o3o` vertex first	`. x4o3o` cube first
2		`x3x4o .`	`x3x . q`	`x . q3o` vertex figure	`. o4q3o`
3a		`x3o4q .`	`x3o . Q`	`u . o3q`	`. x4o3q`
3b		`x3o4q .`	`u3x . o`	`u . o3q`	`. x4o3q`
4a		`x3x4o .`	`x3u . q`	`x . q3q`	`. u4o3o`
4b		`x3x4o .`	`x3u . q`	`H . o3o`	`. u4o3o`
5a		`o3x4o .` opposite co	`x3x . Q`	`o . o3Q`	`. x4o3q`
5b			`H3o . o`
5c			`o3H . o`
6a			`u3x . q`	`x . Q3o`	`. o4q3o`
6b			`u3x . q`	`H . o3q`	`. o4q3o`
7a			`o3x . Q`	`u . q3q`	`. x4o3o` opposite cube
7b			`x3u . o`	`u . q3q`	`. x4o3o` opposite cube
8a			`x3x . q`	`x . o3Q`
8b			`x3x . q`	`H . q3o`
9			`x3o . o` opposite {3}	`o . Q3o`
10a				`x . q3q`
10b				`H . o3o`
11				`u . q3o`
12				`x . o3q`
13				`o . o3o` opposite vertex
	`o3o3o4o`	`o3o3o .`	`o3o . o`	`o . o4o`	`. o3o4o`
1	`x3o3x4o`	`x3o3x .` co first	`x3o . o` {3} first	`x . x4o` cube first	`. o3x4o` co first
2a		`x3x3x .`	`x3x . q`	`u . o4q`	`. x3x4o`
2b		`x3x3x .`	`x3x . q`	`o . u4o`	`. x3x4o`
3a		`u3x3o .`	`o3x . Q`	`H . x4o`	`. x3o4q`
3b		`o3x3u .`	`x3u . o`	`x . x4q`	`. x3o4q`
4		`x3x3x .`	`u3x . q`	`u . u4o`	`. x3x4o`
5a		`x3o3x .` opposite co	`x3x . Q`	`H . x4o`	`. o3x4o` opposite co
5b			`H3o . o`	`x . x4q`
5c			`o3H . o`	`x . x4q`
6a			`x3u . q`	`u . o4q`
6b			`x3u . q`	`o . u4o`
7a			`x3o . Q`	`x . x4o` opposite cube
7b			`u3x . o`	`x . x4o` opposite cube
8			`x3x . q`
9			`o3x . o` opposite {3}
	`o3o3o *b3o`	`o3o3o .`	`o3o . *b3o`	`o . o o`	`. o3o *b3o`
1	`x3o3x *b3x`	`x3o3x .` co first	`x3o . *b3x` co first	`x . x x` cube first	`. o3x *b3x` co first
2a		`x3x3x .`	`x3x . *b3x`	`u . u o`	`. x3x *b3x`
2b				`u . o u`
2c				`o . u u`
3a		`u3x3o .`	`u3x . *b3o`	`x . x H`	`. x3u *b3o`
3b		`o3x3u .`	`o3x . *b3u`	`x . H x`	`. x3o *b3u`
3c		`o3x3u .`	`o3x . *b3u`	`H . x x`	`. x3o *b3u`
4		`x3x3x .`	`x3x . *b3x`	`u . u u`	`. x3x *b3x`
5a		`x3o3x .` opposite co	`x3o . *b3x` opposite co	`x . x H`	`. o3x *b3x` opposite co
5b				`x . H x`
5c				`H . x x`
6a				`u . u o`
6b				`u . o u`
6c				`o . u u`
7				`x . x x` opposite cube

(H=hh=3x, Q=2q)

Lace city
in approx. ASCII-art

©	o3x x3x x3o x3x u3x x3u x3x x3o x3u oH3Ho u3x o3x x3x u3x x3u x3x o3x x3x x3o

©	o3o o3q o3q q3o q3o o3o q3q q3q o3o Q3o q3o o3Q o3Q q3o q3q q3q o3q Q3o Q3o o3q o3Q o3o q3q q3q o3o o3q o3q q3o q3o o3o

©	x4o o4q x4o x4o u4o x4q u4o x4o o4q x4q x4q o4q x4o u4o x4q u4o x4o x4o o4q x4o

Coordinates

(sqrt(2), 1/sqrt(2), 1/sqrt(2), 0) & all permutations, all changes of sign
or wrt. dual positioning of underlying ico:
- (3/2, 1/2, 1/2, 1/2) & all permutations, all changes of sign
  (inscribed q-rits in both demitessic orientations, i.e. a q3o3o4x)
- (1, 1, 1, 0) & all permutations, all changes of sign
  (inscribed q-rit in tessic orientation)

General of army (is itself convex)

Colonel of regiment

(is itself locally convex – uniform polychoral members:

by cells:	co	cube	oho	toe
rico	24	24	0	0
ini	24	0	0	24
rawvhitto	8	0	16	8
frico	0	24	0	24

& others)

Dihedral angles

at {4} between co and cube: 135°
at {3} between co and co: 120°

Face vector 96, 288, 240, 48

Confer

Grünbaumian relatives:: 2rico 2rico+64{6}+128{3} 2rico+64{6}+192{3}
segmentochora:: coatoe
related CRFs:: dirico pabdirico cytid rico qo2ox3xx4oo&#zx
related isogonals:: spidrico
decompositions:: ico || rico
related Gévay polytopes:: oq3oo3qo3oc&#zx oq3oo3qo5oc&#zx oa3oo4bo3oc&#zx oa4oo3bo3oc&#zx oa5oo3bo3oc&#zx xuo3uoo3oou3oux&#z(q,q,h) aco3boo4oob3oca&#z(x,x,d)
ambification:: rerico
ambification pre-image:: ico
general polytopal classes:: Wythoffian polychora lace simplices partial Stott expansions

External
links

Note that rico can be thought of as the external blend of 1 ico + 24 octacoes + 24 cubpies. This decomposition is described as the degenerate segmentoteron xo3ox4oo3oo&#x.

Incidence matrix according to Dynkin symbol

o3x4o3o

. . . . | 96 ♦   6 |  3   6 |  3  2
--------+----+-----+--------+------
. x . . |  2 | 288 |  1   2 |  2  1
--------+----+-----+--------+------
o3x . . |  3 |   3 | 96   * |  2  0
. x4o . |  4 |   4 |  * 144 |  1  1
--------+----+-----+--------+------
o3x4o . ♦ 12 |  24 |  8   6 | 24  *
. x4o3o ♦  8 |  12 |  0   6 |  * 24

snubbed forms: o3β4o3o

o3x4o3/2o

. . .   . | 96 ♦   6 |  3   6 |  3  2
----------+----+-----+--------+------
. x .   . |  2 | 288 |  1   2 |  2  1
----------+----+-----+--------+------
o3x .   . |  3 |   3 | 96   * |  2  0
. x4o   . |  4 |   4 |  * 144 |  1  1
----------+----+-----+--------+------
o3x4o   . ♦ 12 |  24 |  8   6 | 24  *
. x4o3/2o ♦  8 |  12 |  0   6 |  * 24

o3x4/3o3o

. .   . . | 96 ♦   6 |  3   6 |  3  2
----------+----+-----+--------+------
. x   . . |  2 | 288 |  1   2 |  2  1
----------+----+-----+--------+------
o3x   . . |  3 |   3 | 96   * |  2  0
. x4/3o . |  4 |   4 |  * 144 |  1  1
----------+----+-----+--------+------
o3x4/3o . ♦ 12 |  24 |  8   6 | 24  *
. x4/3o3o ♦  8 |  12 |  0   6 |  * 24

o3x4/3o3/2o

. .   .   . | 96 ♦   6 |  3   6 |  3  2
------------+----+-----+--------+------
. x   .   . |  2 | 288 |  1   2 |  2  1
------------+----+-----+--------+------
o3x   .   . |  3 |   3 | 96   * |  2  0
. x4/3o   . |  4 |   4 |  * 144 |  1  1
------------+----+-----+--------+------
o3x4/3o   . ♦ 12 |  24 |  8   6 | 24  *
. x4/3o3/2o ♦  8 |  12 |  0   6 |  * 24

o3/2x4o3o

.   . . . | 96 ♦   6 |  3   6 |  3  2
----------+----+-----+--------+------
.   x . . |  2 | 288 |  1   2 |  2  1
----------+----+-----+--------+------
o3/2x . . |  3 |   3 | 96   * |  2  0
.   x4o . |  4 |   4 |  * 144 |  1  1
----------+----+-----+--------+------
o3/2x4o . ♦ 12 |  24 |  8   6 | 24  *
.   x4o3o ♦  8 |  12 |  0   6 |  * 24

o3/2x4o3/2o

.   . .   . | 96 ♦   6 |  3   6 |  3  2
------------+----+-----+--------+------
.   x .   . |  2 | 288 |  1   2 |  2  1
------------+----+-----+--------+------
o3/2x .   . |  3 |   3 | 96   * |  2  0
.   x4o   . |  4 |   4 |  * 144 |  1  1
------------+----+-----+--------+------
o3/2x4o   . ♦ 12 |  24 |  8   6 | 24  *
.   x4o3/2o ♦  8 |  12 |  0   6 |  * 24

o3/2x4/3o3o

.   .   . . | 96 ♦   6 |  3   6 |  3  2
------------+----+-----+--------+------
.   x   . . |  2 | 288 |  1   2 |  2  1
------------+----+-----+--------+------
o3/2x   . . |  3 |   3 | 96   * |  2  0
.   x4/3o . |  4 |   4 |  * 144 |  1  1
------------+----+-----+--------+------
o3/2x4/3o . ♦ 12 |  24 |  8   6 | 24  *
.   x4/3o3o ♦  8 |  12 |  0   6 |  * 24

o3/2x4/3o3/2o

.   .   .   . | 96 ♦   6 |  3   6 |  3  2
--------------+----+-----+--------+------
.   x   .   . |  2 | 288 |  1   2 |  2  1
--------------+----+-----+--------+------
o3/2x   .   . |  3 |   3 | 96   * |  2  0
.   x4/3o   . |  4 |   4 |  * 144 |  1  1
--------------+----+-----+--------+------
o3/2x4/3o   . ♦ 12 |  24 |  8   6 | 24  *
.   x4/3o3/2o ♦  8 |  12 |  0   6 |  * 24

x3o3x4o

. . . . | 96 ♦  2   4 |  1  4  2  2 |  2  2 1
--------+----+--------+-------------+--------
x . . . |  2 | 96   * |  1  2  0  0 |  2  1 0
. . x . |  2 |  * 192 |  0  1  1  1 |  1  1 1
--------+----+--------+-------------+--------
x3o . . |  3 |  3   0 | 32  *  *  * |  2  0 0
x . x . |  4 |  2   2 |  * 96  *  * |  1  1 0
. o3x . |  3 |  0   3 |  *  * 64  * |  1  0 1
. . x4o |  4 |  0   4 |  *  *  * 48 |  0  1 1
--------+----+--------+-------------+--------
x3o3x . ♦ 12 | 12  12 |  4  6  4  0 | 16  * *
x . x4o ♦  8 |  4   8 |  0  4  0  2 |  * 24 *
. o3x4o ♦ 12 |  0  24 |  0  0  8  6 |  *  * 8

snubbed forms: β3o3x4o, x3o3β4o, β3o3β4o

x3o3x4/3o

. . .   . | 96 ♦  2   4 |  1  4  2  2 |  2  2 1
----------+----+--------+-------------+--------
x . .   . |  2 | 96   * |  1  2  0  0 |  2  1 0
. . x   . |  2 |  * 192 |  0  1  1  1 |  1  1 1
----------+----+--------+-------------+--------
x3o .   . |  3 |  3   0 | 32  *  *  * |  2  0 0
x . x   . |  4 |  2   2 |  * 96  *  * |  1  1 0
. o3x   . |  3 |  0   3 |  *  * 64  * |  1  0 1
. . x4/3o |  4 |  0   4 |  *  *  * 48 |  0  1 1
----------+----+--------+-------------+--------
x3o3x   . ♦ 12 | 12  12 |  4  6  4  0 | 16  * *
x . x4/3o ♦  8 |  4   8 |  0  4  0  2 |  * 24 *
. o3x4/3o ♦ 12 |  0  24 |  0  0  8  6 |  *  * 8

x3/2o3/2x4o

.   .   . . | 96 ♦  2   4 |  1  4  2  2 |  2  2 1
------------+----+--------+-------------+--------
x   .   . . |  2 | 96   * |  1  2  0  0 |  2  1 0
.   .   x . |  2 |  * 192 |  0  1  1  1 |  1  1 1
------------+----+--------+-------------+--------
x3/2o   . . |  3 |  3   0 | 32  *  *  * |  2  0 0
x   .   x . |  4 |  2   2 |  * 96  *  * |  1  1 0
.   o3/2x . |  3 |  0   3 |  *  * 64  * |  1  0 1
.   .   x4o |  4 |  0   4 |  *  *  * 48 |  0  1 1
------------+----+--------+-------------+--------
x3/2o3/2x . ♦ 12 | 12  12 |  4  6  4  0 | 16  * *
x   .   x4o ♦  8 |  4   8 |  0  4  0  2 |  * 24 *
.   o3/2x4o ♦ 12 |  0  24 |  0  0  8  6 |  *  * 8

x3/2o3/2x4/3o

.   .   .   . | 96 ♦  2   4 |  1  4  2  2 |  2  2 1
--------------+----+--------+-------------+--------
x   .   .   . |  2 | 96   * |  1  2  0  0 |  2  1 0
.   .   x   . |  2 |  * 192 |  0  1  1  1 |  1  1 1
--------------+----+--------+-------------+--------
x3/2o   .   . |  3 |  3   0 | 32  *  *  * |  2  0 0
x   .   x   . |  4 |  2   2 |  * 96  *  * |  1  1 0
.   o3/2x   . |  3 |  0   3 |  *  * 64  * |  1  0 1
.   .   x4/3o |  4 |  0   4 |  *  *  * 48 |  0  1 1
--------------+----+--------+-------------+--------
x3/2o3/2x   . ♦ 12 | 12  12 |  4  6  4  0 | 16  * *
x   .   x4/3o ♦  8 |  4   8 |  0  4  0  2 |  * 24 *
.   o3/2x4/3o ♦ 12 |  0  24 |  0  0  8  6 |  *  * 8

x3o3x *b3x

. . .    . | 96 ♦  2  2  2 |  1  2  2  1  2  1 | 1 1  2 1
-----------+----+----------+-------------------+---------
x . .    . |  2 | 96  *  * |  1  1  1  0  0  0 | 1 1  1 0
. . x    . |  2 |  * 96  * |  0  1  0  1  1  0 | 1 0  1 1
. . .    x |  2 |  *  * 96 |  0  0  1  0  1  1 | 0 1  1 1
-----------+----+----------+-------------------+---------
x3o .    . |  3 |  3  0  0 | 32  *  *  *  *  * | 1 1  0 0
x . x    . |  4 |  2  2  0 |  * 48  *  *  *  * | 1 0  1 0
x . .    x |  4 |  2  0  2 |  *  * 48  *  *  * | 0 1  1 0
. o3x    . |  3 |  0  3  0 |  *  *  * 32  *  * | 1 0  0 1
. . x    x |  4 |  0  2  2 |  *  *  *  * 48  * | 0 0  1 1
  o . *b3x |  3 |  0  0  3 |  *  *  *  *  * 32 | 0 1  0 1
-----------+----+----------+-------------------+---------
x3o3x    . ♦ 12 | 12 12  0 |  4  6  0  4  0  0 | 8 *  * *
x3o . *b3x ♦ 12 | 12  0 12 |  4  0  6  0  0  4 | * 8  * *
x . x    x ♦  8 |  4  4  4 |  0  2  2  0  2  0 | * * 24 *
. o3x *b3x ♦ 12 |  0 12 12 |  0  0  0  4  6  4 | * *  * 8

snubbed forms: β3o3x *b3x, β3o3β *b3x, β3o3β *b3β

x3/2o3/2x *b3/2x

.   .   .      . | 96 ♦  2  2  2 |  1  2  2  1  2  1 | 1 1  2 1
-----------------+----+----------+-------------------+---------
x   .   .      . |  2 | 96  *  * |  1  1  1  0  0  0 | 1 1  1 0
.   .   x      . |  2 |  * 96  * |  0  1  0  1  1  0 | 1 0  1 1
.   .   .      x |  2 |  *  * 96 |  0  0  1  0  1  1 | 0 1  1 1
-----------------+----+----------+-------------------+---------
x3/2o   .      . |  3 |  3  0  0 | 32  *  *  *  *  * | 1 1  0 0
x   .   x      . |  4 |  2  2  0 |  * 48  *  *  *  * | 1 0  1 0
x   .   .      x |  4 |  2  0  2 |  *  * 48  *  *  * | 0 1  1 0
.   o3/2x      . |  3 |  0  3  0 |  *  *  * 32  *  * | 1 0  0 1
.   .   x      x |  4 |  0  2  2 |  *  *  *  * 48  * | 0 0  1 1
.   o   . *b3/2x |  3 |  0  0  3 |  *  *  *  *  * 32 | 0 1  0 1
-----------------+----+----------+-------------------+---------
x3/2o3/2x      . ♦ 12 | 12 12  0 |  4  6  0  4  0  0 | 8 *  * *
x3/2o   . *b3/2x ♦ 12 | 12  0 12 |  4  0  6  0  0  4 | * 8  * *
x   .   x      x ♦  8 |  4  4  4 |  0  2  2  0  2  0 | * * 24 *
.   o3/2x *b3/2x ♦ 12 |  0 12 12 |  0  0  0  4  6  4 | * *  * 8

s4x3o3x

demi( . . . . ) | 96 ♦  2  2  2 |  2  1  2  1  1  2 | 1  2 1 1
----------------+----+----------+-------------------+---------
demi( . x . . ) |  2 | 96  *  * |  1  1  1  0  0  0 | 1  1 1 0
demi( . . . x ) |  2 |  * 96  * |  0  0  1  1  0  1 | 0  1 1 1
sefa( s4x . . ) |  2 |  *  * 96 |  1  0  0  0  1  1 | 1  1 0 1
----------------+----+----------+-------------------+---------
      s4x . .   ♦  4 |  2  0  2 | 48  *  *  *  *  * | 1  1 0 0
demi( . x3o . ) |  3 |  3  0  0 |  * 32  *  *  *  * | 1  0 1 0
demi( . x . x ) |  4 |  2  2  0 |  *  * 48  *  *  * | 0  1 1 0
demi( . . o3x ) |  3 |  0  3  0 |  *  *  * 32  *  * | 0  0 1 1
sefa( s4x3o . ) |  3 |  0  0  3 |  *  *  *  * 32  * | 1  0 0 1
sefa( s4x 2 x ) |  4 |  0  2  2 |  *  *  *  *  * 48 | 0  1 0 1
----------------+----+----------+-------------------+---------
      s4x3o .   ♦ 12 | 12  0 12 |  6  4  0  0  4  0 | 8  * * *
      s4x 2 x   ♦  8 |  4  4  4 |  2  0  2  0  0  2 | * 24 * *
demi( . x3o3x ) ♦ 12 | 12 12  0 |  0  4  6  4  0  0 | *  * 8 *
sefa( s4x3o3x ) ♦ 12 |  0 12 12 |  0  0  0  4  4  6 | *  * * 8

starting figure: x4x3o3x

oxxxo3xxoxx4ooqoo&#xt   → all heights = 1/sqrt(2) = 0.707107
(co || pseudo toe || pseudo reco || pseudo toe || co)

o....3o....4o....     | 12  *  *  *  * ♦  4  2  0  0  0  0  0  0  0  0  0 | 2 2  1  4 0  0  0  0 0  0  0 0  0  0 0 0 | 1 2 2  0 0 0 0 0
.o...3.o...4.o...     |  * 24  *  *  * ♦  0  1  1  2  2  0  0  0  0  0  0 | 0 0  1  2 1  2  2  1 0  0  0 0  0  0 0 0 | 0 2 1  1 1 0 0 0
..o..3..o..4..o..     |  *  * 24  *  * ♦  0  0  0  0  2  2  2  0  0  0  0 | 0 0  0  0 0  2  1  2 1  2  1 0  0  0 0 0 | 0 1 0  2 1 1 0 0
...o.3...o.4...o.     |  *  *  * 24  * ♦  0  0  0  0  0  0  2  1  2  1  0 | 0 0  0  0 0  0  0  1 0  2  2 1  1  2 0 0 | 0 0 0  1 1 2 1 0
....o3....o4....o     |  *  *  *  * 12 ♦  0  0  0  0  0  0  0  0  0  2  4 | 0 0  0  0 0  0  0  0 0  0  0 0  1  4 2 2 | 0 0 0  0 0 2 2 1
----------------------+----------------+----------------------------------+------------------------------------------+-----------------
..... x.... .....     |  2  0  0  0  0 | 24  *  *  *  *  *  *  *  *  *  * | 1 1  0  1 0  0  0  0 0  0  0 0  0  0 0 0 | 1 1 1  0 0 0 0 0
oo...3oo...4oo...&#x  |  1  1  0  0  0 |  * 24  *  *  *  *  *  *  *  *  * | 0 0  1  2 0  0  0  0 0  0  0 0  0  0 0 0 | 0 2 1  0 0 0 0 0
.x... ..... .....     |  0  2  0  0  0 |  *  * 12  *  *  *  *  *  *  *  * | 0 0  1  0 0  2  0  0 0  0  0 0  0  0 0 0 | 0 2 0  1 0 0 0 0
..... .x... .....     |  0  2  0  0  0 |  *  *  * 24  *  *  *  *  *  *  * | 0 0  0  1 1  0  1  0 0  0  0 0  0  0 0 0 | 0 1 1  0 1 0 0 0
.oo..3.oo..4.oo..&#x  |  0  1  1  0  0 |  *  *  *  * 48  *  *  *  *  *  * | 0 0  0  0 0  1  1  1 0  0  0 0  0  0 0 0 | 0 1 0  1 1 0 0 0
..x.. ..... .....     |  0  0  2  0  0 |  *  *  *  *  * 24  *  *  *  *  * | 0 0  0  0 0  1  0  0 1  1  0 0  0  0 0 0 | 0 1 0  1 0 1 0 0
..oo.3..oo.4..oo.&#x  |  0  0  1  1  0 |  *  *  *  *  *  * 48  *  *  *  * | 0 0  0  0 0  0  0  1 0  1  1 0  0  0 0 0 | 0 0 0  1 1 1 0 0
...x. ..... .....     |  0  0  0  2  0 |  *  *  *  *  *  *  * 12  *  *  * | 0 0  0  0 0  0  0  0 0  2  0 0  1  0 0 0 | 0 0 0  1 0 2 0 0
..... ...x. .....     |  0  0  0  2  0 |  *  *  *  *  *  *  *  * 24  *  * | 0 0  0  0 0  0  0  0 0  0  1 1  0  1 0 0 | 0 0 0  0 1 1 1 0
...oo3...oo4...oo&#x  |  0  0  0  1  1 |  *  *  *  *  *  *  *  *  * 24  * | 0 0  0  0 0  0  0  0 0  0  0 0  1  2 0 0 | 0 0 0  0 0 2 1 0
..... ....x .....     |  0  0  0  0  2 |  *  *  *  *  *  *  *  *  *  * 24 | 0 0  0  0 0  0  0  0 0  0  0 0  0  1 1 1 | 0 0 0  0 0 1 1 1
----------------------+----------------+----------------------------------+------------------------------------------+-----------------
o....3x.... .....     |  3  0  0  0  0 |  3  0  0  0  0  0  0  0  0  0  0 | 8 *  *  * *  *  *  * *  *  * *  *  * * * | 1 1 0  0 0 0 0 0
..... x....4o....     |  4  0  0  0  0 |  4  0  0  0  0  0  0  0  0  0  0 | * 6  *  * *  *  *  * *  *  * *  *  * * * | 1 0 1  0 0 0 0 0
ox... ..... .....&#x  |  1  2  0  0  0 |  0  2  1  0  0  0  0  0  0  0  0 | * * 12  * *  *  *  * *  *  * *  *  * * * | 0 2 0  0 0 0 0 0
..... xx... .....&#x  |  2  2  0  0  0 |  1  2  0  1  0  0  0  0  0  0  0 | * *  * 24 *  *  *  * *  *  * *  *  * * * | 0 1 1  0 0 0 0 0
..... .x...4.o...     |  0  4  0  0  0 |  0  0  0  4  0  0  0  0  0  0  0 | * *  *  * 6  *  *  * *  *  * *  *  * * * | 0 0 1  0 1 0 0 0
.xx.. ..... .....&#x  |  0  2  2  0  0 |  0  0  1  0  2  1  0  0  0  0  0 | * *  *  * * 24  *  * *  *  * *  *  * * * | 0 1 0  1 0 0 0 0
..... .xo.. .....&#x  |  0  2  1  0  0 |  0  0  0  1  2  0  0  0  0  0  0 | * *  *  * *  * 24  * *  *  * *  *  * * * | 0 1 0  0 1 0 0 0
..... ..... .oqo.&#xt |  0  1  2  1  0 |  0  0  0  0  2  0  2  0  0  0  0 | * *  *  * *  *  * 24 *  *  * *  *  * * * | 0 0 0  1 1 0 0 0
..x..3..o.. .....     |  0  0  3  0  0 |  0  0  0  0  0  3  0  0  0  0  0 | * *  *  * *  *  *  * 8  *  * *  *  * * * | 0 1 0  0 0 1 0 0
..xx. ..... .....&#x  |  0  0  2  2  0 |  0  0  0  0  0  1  2  1  0  0  0 | * *  *  * *  *  *  * * 24  * *  *  * * * | 0 0 0  1 0 1 0 0
..... ..ox. .....&#x  |  0  0  1  2  0 |  0  0  0  0  0  0  2  0  1  0  0 | * *  *  * *  *  *  * *  * 24 *  *  * * * | 0 0 0  0 1 1 0 0
..... ...x.4...o.     |  0  0  0  4  0 |  0  0  0  0  0  0  0  0  4  0  0 | * *  *  * *  *  *  * *  *  * 6  *  * * * | 0 0 0  0 1 0 1 0
...xo ..... .....&#x  |  0  0  0  2  1 |  0  0  0  0  0  0  0  1  0  2  0 | * *  *  * *  *  *  * *  *  * * 12  * * * | 0 0 0  0 0 2 0 0
..... ...xx .....&#x  |  0  0  0  2  2 |  0  0  0  0  0  0  0  0  1  2  1 | * *  *  * *  *  *  * *  *  * *  * 24 * * | 0 0 0  0 0 1 1 0
....o3....x .....     |  0  0  0  0  3 |  0  0  0  0  0  0  0  0  0  0  3 | * *  *  * *  *  *  * *  *  * *  *  * 8 * | 0 0 0  0 0 1 0 1
..... ....x4....o     |  0  0  0  0  4 |  0  0  0  0  0  0  0  0  0  0  4 | * *  *  * *  *  *  * *  *  * *  *  * * 6 | 0 0 0  0 0 0 1 1
----------------------+----------------+----------------------------------+------------------------------------------+-----------------
o....3x....4o....     ♦ 12  0  0  0  0 | 24  0  0  0  0  0  0  0  0  0  0 | 8 6  0  0 0  0  0  0 0  0  0 0  0  0 0 0 | 1 * *  * * * * *
oxx..3xxo.. .....&#xt ♦  3  6  3  0  0 |  3  6  3  3  6  3  0  0  0  0  0 | 1 0  3  3 0  3  3  0 1  0  0 0  0  0 0 0 | * 8 *  * * * * *
..... xx...4oo...&#x  ♦  4  4  0  0  0 |  4  4  0  4  0  0  0  0  0  0  0 | 0 1  0  4 1  0  0  0 0  0  0 0  0  0 0 0 | * * 6  * * * * *
.xxx. ..... .oqo.&#xt ♦  0  2  4  2  0 |  0  0  1  0  4  2  4  1  0  0  0 | 0 0  0  0 0  2  0  2 0  2  0 0  0  0 0 0 | * * * 12 * * * *
..... .xox.4.oqo.&#xt ♦  0  4  4  4  0 |  0  0  0  4  8  0  8  0  4  0  0 | 0 0  0  0 1  0  4  4 0  0  4 1  0  0 0 0 | * * *  * 6 * * *
..xxo3..oxx .....&#xt ♦  0  0  3  6  3 |  0  0  0  0  0  3  6  3  3  6  3 | 0 0  0  0 0  0  0  0 1  3  3 0  3  3 1 0 | * * *  * * 8 * *
..... ...xx4...oo&#x  ♦  0  0  0  4  4 |  0  0  0  0  0  0  0  0  4  4  4 | 0 0  0  0 0  0  0  0 0  0  0 1  0  4 0 1 | * * *  * * * 6 *
....o3....x4....o     ♦  0  0  0  0 12 |  0  0  0  0  0  0  0  0  0  0 24 | 0 0  0  0 0  0  0  0 0  0  0 0  0  0 8 6 | * * *  * * * * 1

or
o....3o....4o....      & | 24  *  * ♦  4  2  0  0  0  0 |  2  2  1  4  0  0  0  0 0 | 1  2  2  0 0
.o...3.o...4.o...      & |  * 48  * ♦  0  1  1  2  2  0 |  0  0  1  2  1  2  2  1 0 | 0  2  1  1 1
..o..3..o..4..o..        |  *  * 24 ♦  0  0  0  0  4  2 |  0  0  0  0  0  4  2  2 1 | 0  2  0  2 1
-------------------------+----------+-------------------+---------------------------+-------------
..... x.... .....      & |  2  0  0 | 48  *  *  *  *  * |  1  1  0  1  0  0  0  0 0 | 1  1  1  0 0
oo...3oo...4oo...&#x   & |  1  1  0 |  * 48  *  *  *  * |  0  0  1  2  0  0  0  0 0 | 0  2  1  0 0
.x... ..... .....      & |  0  2  0 |  *  * 24  *  *  * |  0  0  1  0  0  2  0  0 0 | 0  2  0  1 0
..... .x... .....      & |  0  2  0 |  *  *  * 48  *  * |  0  0  0  1  1  0  1  0 0 | 0  1  1  0 1
.oo..3.oo..4.oo..&#x   & |  0  1  1 |  *  *  *  * 96  * |  0  0  0  0  0  1  1  1 0 | 0  1  0  1 1
..x.. ..... .....        |  0  0  2 |  *  *  *  *  * 24 |  0  0  0  0  0  2  0  0 1 | 0  2  0  1 0
-------------------------+----------+-------------------+---------------------------+-------------
o....3x.... .....      & |  3  0  0 |  3  0  0  0  0  0 | 16  *  *  *  *  *  *  * * | 1  1  0  0 0
..... x....4o....      & |  4  0  0 |  4  0  0  0  0  0 |  * 12  *  *  *  *  *  * * | 1  0  1  0 0
ox... ..... .....&#x   & |  1  2  0 |  0  2  1  0  0  0 |  *  * 24  *  *  *  *  * * | 0  2  0  0 0
..... xx... .....&#x   & |  2  2  0 |  1  2  0  1  0  0 |  *  *  * 48  *  *  *  * * | 0  1  1  0 0
..... .x...4.o...      & |  0  4  0 |  0  0  0  4  0  0 |  *  *  *  * 12  *  *  * * | 0  0  1  0 1
.xx.. ..... .....&#x   & |  0  2  2 |  0  0  1  0  2  1 |  *  *  *  *  * 48  *  * * | 0  1  0  1 0
..... .xo.. .....&#x   & |  0  2  1 |  0  0  0  1  2  0 |  *  *  *  *  *  * 48  * * | 0  1  0  0 1
..... ..... .oqo.&#xt    |  0  2  2 |  0  0  0  0  4  0 |  *  *  *  *  *  *  * 24 * | 0  0  0  1 1
..x..3..o.. .....        |  0  0  3 |  0  0  0  0  0  3 |  *  *  *  *  *  *  *  * 8 | 0  2  0  0 0
-------------------------+----------+-------------------+---------------------------+-------------
o....3x....4o....      & ♦ 12  0  0 | 24  0  0  0  0  0 |  8  6  0  0  0  0  0  0 0 | 2  *  *  * *
oxx..3xxo.. .....&#xt  & ♦  3  6  3 |  3  6  3  3  6  3 |  1  0  3  3  0  3  3  0 1 | * 16  *  * *
..... xx...4oo...&#x   & ♦  4  4  0 |  4  4  0  4  0  0 |  0  1  0  4  1  0  0  0 0 | *  * 12  * *
.xxx. ..... .oqo.&#xt    ♦  0  4  4 |  0  0  2  0  8  2 |  0  0  0  0  0  4  0  2 0 | *  *  * 12 *
..... .xox.4.oqo.&#xt    ♦  0  8  4 |  0  0  0  8 16  0 |  0  0  0  0  2  0  8  4 0 | *  *  *  * 6

ooqoqoo3oqoooqo4xoxuxox&#xt   → all heights = 1/2
(cube || pseudo q-co || pseudo (x,q)-sirco || pseudo u-cube || pseudo (x,q)-sirco || pseudo q-co || cube)

o......3o......4o......      & | 16  *  * * ♦  3  3  0  0  0  0 |  3  3  3  0  0  0  0  0 | 1  3  1  0 0
.o.....3.o.....4.o.....      & |  * 24  * * ♦  0  2  4  0  0  0 |  0  1  4  2  2  0  0  0 | 0  2  2  1 0
..o....3..o....4..o....      & |  *  * 48 * ♦  0  0  2  2  1  1 |  0  0  1  2  2  1  2  1 | 0  1  1  2 1
...o...3...o...4...o...        |  *  *  * 8 ♦  0  0  0  0  6  0 |  0  0  0  0  6  0  0  3 | 0  0  2  3 0
-------------------------------+------------+-------------------+-------------------------+-------------
....... ....... x......      & |  2  0  0 0 | 24  *  *  *  *  * |  2  1  0  0  0  0  0  0 | 1  2  0  0 0
oo.....3oo.....4oo.....&#x   & |  1  1  0 0 |  * 48  *  *  *  * |  0  1  2  0  0  0  0  0 | 0  2  1  0 0
.oo....3.oo....4.oo....&#x   & |  0  1  1 0 |  *  * 96  *  *  * |  0  0  1  1  1  0  0  0 | 0  1  1  1 0
....... ....... ..x....      & |  0  0  2 0 |  *  *  * 48  *  * |  0  0  0  1  0  1  1  0 | 0  1  0  1 1
..oo...3..oo...4..oo...&#x   & |  0  0  1 1 |  *  *  *  * 48  * |  0  0  0  0  2  0  0  1 | 0  0  1  2 0
..o.o..3..o.o..4..o.o..&#x     |  0  0  2 0 |  *  *  *  *  * 24 |  0  0  0  0  0  0  2  1 | 0  0  0  2 1
-------------------------------+------------+-------------------+-------------------------+-------------
....... o......4x......      & |  4  0  0 0 |  4  0  0  0  0  0 | 12  *  *  *  *  *  *  * | 1  1  0  0 0
....... ....... xo.....&#x   & |  2  1  0 0 |  1  2  0  0  0  0 |  * 24  *  *  *  *  *  * | 0  2  0  0 0
....... oqo.... .......&#xt  & |  1  2  1 0 |  0  2  2  0  0  0 |  *  * 48  *  *  *  *  * | 0  1  1  0 0
....... ....... .ox....&#x   & |  0  1  2 0 |  0  0  2  1  0  0 |  *  *  * 48  *  *  *  * | 0  1  0  1 0
.oqo... ....... .......&#xt  & |  0  1  2 1 |  0  0  2  0  2  0 |  *  *  *  * 48  *  *  * | 0  0  1  1 0
....... ..o....4..x....      & |  0  0  4 0 |  0  0  0  4  0  0 |  *  *  *  *  * 12  *  * | 0  1  0  0 1
....... ....... ..x.x..&#x     |  0  0  4 0 |  0  0  0  2  0  2 |  *  *  *  *  *  * 24  * | 0  0  0  1 1
..ooo..3..ooo..4..ooo..&#xt    |  0  0  2 1 |  0  0  0  0  2  1 |  *  *  *  *  *  *  * 24 | 0  0  0  2 0
-------------------------------+------------+-------------------+-------------------------+-------------
o......3o......4x......      & ♦  8  0  0 0 | 12  0  0  0  0  0 |  6  0  0  0  0  0  0  0 | 2  *  *  * *
....... oqo....4xox....&#xt  & ♦  4  4  4 0 |  4  8  8  4  0  0 |  1  4  4  4  0  1  0  0 | * 12  *  * *
ooqo...3oqoo... .......&#xt  & ♦  1  3  3 1 |  0  3  6  0  3  0 |  0  0  3  0  3  0  0  0 | *  * 16  * *
.oqoqo. ....... .oxuxo.&#xt    ♦  0  2  8 2 |  0  0  8  4  8  4 |  0  0  0  4  4  0  2  4 | *  *  * 12 *
....... ..o.o..4..x.x..&#x     ♦  0  0  8 0 |  0  0  0  8  0  4 |  0  0  0  0  0  2  4  0 | *  *  *  * 6

qoq3ooo3qqo *b3oqq&#zx   → height = 0
(tegum sum of 3 mutually gyrated q-rits)

o..3o..3o.. *b3o..     & | 96 ♦   6 |   6  3 |  2  3
-------------------------+----+-----+--------+------
oo.3oo.3oo. *b3oo.&#x  & |  2 | 288 |   2  1 |  1  2
-------------------------+----+-----+--------+------
qo. ... ...    oq.&#zx & |  4 |   4 | 144  * |  1  1
ooo3ooo3ooo *b3ooo&#x    |  3 |   3 |   * 96 |  0  2
-------------------------+----+-----+--------+------
qo.3oo. ... *b3oq.&#zx & ♦  8 |  12 |   6  0 | 24  *
qoq ... qqo    oqq&#zx   ♦ 12 |  24 |   6  8 |  * 24

qo3oo3oq4xo&#zx   → height = 0
(tegum sum of (q,x)-sidpith and q-rit)

o.3o.3o.4o.     | 64  * ♦  3   3 |  3  3  3 | 1  1  3
.o3.o3.o4.o     |  * 32 ♦  0   6 |  0  6  3 | 0  2  3
----------------+-------+--------+----------+--------
.. .. .. x.     |  2  0 | 96   * |  2  0  1 | 1  0  2
oo3oo3oo4oo&#x  |  1  1 |  * 192 |  0  2  1 | 0  1  2
----------------+-------+--------+----------+--------
.. .. o.4x.     |  4  0 |  4   0 | 48  *  * | 1  0  1
qo .. oq ..&#zx |  2  2 |  0   4 |  * 96  * | 0  1  1
.. .. .. xo&#x  |  2  1 |  1   2 |  *  * 96 | 0  0  2
----------------+-------+--------+----------+--------
.. o.3o.4x.     ♦  8  0 | 12   0 |  6  0  0 | 8  *  *
qo3oo3oq ..&#zx ♦  4  4 |  0  12 |  0  6  0 | * 16  *
qo .. oq4xo&#zx ♦  8  4 |  8  16 |  2  4  8 | *  * 24

top of page