tho

Acronym	tho
Name	tesseractihemioctachoron, octahemioctachoron, vertex figure of hehad
Cross sections	©
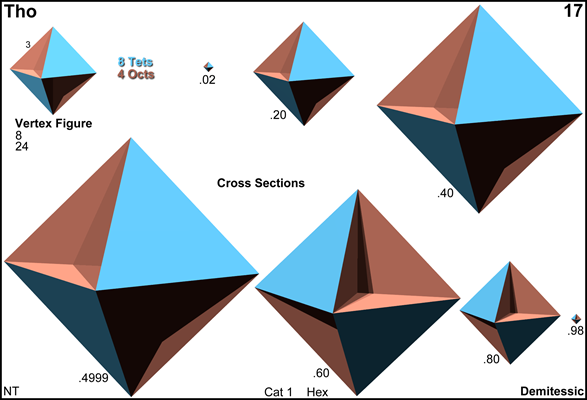Circumradius	1/sqrt(2) = 0.707107
Inradius wrt. tet	1/sqrt(8) = 0.353553
Inradius wrt. oct	0
Coordinates	in orthoplex position: (1/sqrt(2), 0, 0, 0) & all permutations, all changes of sign in hemitesseract position: (1/sqrt(8), 1/sqrt(8), 1/sqrt(8), 1/sqrt(8)) & all even permutations, all even changes of sign in "the other" (mirrored) hemitesseract position: (1/sqrt(8), 1/sqrt(8), 1/sqrt(8), -1/sqrt(8)) & all even permutations, all even changes of sign
Surface	sqrt(8) = 2.828427
General of army	hex
Colonel of regiment	hex
Dihedral angles (at margins)	at {3} between oct and tet: 60°
Face vector	8, 24, 32, 12
Confer	Grünbaumian relatives: 2tho 2tho+24{4} ox3/2ox3xo&#x general polytopal classes: segmentochora non-orientable analogs: demicross hO_n
External links

This polychoron could also be understood as a modwrap of octet.

Two of the below matrices are representing tho as ridge facetings of hex in the facet first orientation thereof. However, because tho reuses just alternate tets thereof, this one can be given in its (true) tet first or its pseudo cell first orientation. Note the differences of the layer participations of the in here remaining tets in those matrices.

Incidence matrix

  8 ♦  6 | 12 | 4 3
----+----+----+----
  2 | 24 |  4 | 2 2
----+----+----+----
  3 |  3 | 32 | 1 1
----+----+----+----
♦ 4 |  6 |  4 | 8 *
♦ 6 | 12 |  8 | * 4

(pseudo tet first orientation)

  4 * | 3  3 0 | 3  6  3 0 | 3 3 1
  * 4 | 0  3 3 | 0  3  6 3 | 1 3 3
------+--------+-----------+------
  2 0 | 6  * * | 2  2  0 0 | 2 2 0
  1 1 | * 12 * | 0  2  2 0 | 1 2 1
  0 2 | *  * 6 | 0  0  2 2 | 0 2 2
------+--------+-----------+------
  3 0 | 3  0 0 | 4  *  * * | 1 1 0
  2 1 | 1  2 0 | * 12  * * | 1 1 0
  1 2 | 0  2 1 | *  * 12 * | 0 1 1
  0 3 | 0  0 3 | *  *  * 4 | 0 1 1
------+--------+-----------+------
♦ 3 1 | 3  3 0 | 1  3  0 0 | 4 * *
♦ 3 3 | 3  6 3 | 1  3  3 1 | * 4 *
♦ 1 3 | 0  3 3 | 0  0  3 1 | * * 4

(tet first orientation)
reduced( ox3/2ox3xo&#x, by base 2tet )

         o.3/2o.3o.                        | 4 * | 3  3 0 | 3  3  6 0 | 1 3 3 0
reduced( .o3/2.o3.o    )                   | * 4 | 0  3 3 | 0  6  3 3 | 0 3 3 1
-------------------------------------------+-----+--------+-----------+--------
         ..   .. x.                        | 2 0 | 6  * * | 2  0  2 0 | 1 1 2 0
reduced( oo3/2oo3oo&#x )                   | 1 1 | * 12 * | 0  2  2 0 | 0 2 2 0
reduced( .x   .. ..     &  ..   .x ..    ) | 0 2 | *  * 6 | 0  2  0 2 | 0 1 2 1
-------------------------------------------+-----+--------+-----------+--------
         ..   o.3x.                        | 3 0 | 3  0 0 | 4  *  * * | 1 0 1 0
reduced( ox   .. ..&#x  &  ..   ox ..&#x ) | 1 2 | 0  2 1 | * 12  * * | 0 1 1 0
         ..   .. xo&#x                     | 2 1 | 1  2 0 | *  * 12 * | 0 1 1 0
         ..   .x3.o                        | 0 3 | 0  0 3 | *  *  * 4 | 0 0 1 1
-------------------------------------------+-----+--------+-----------+--------
         o.3/2o.3x.                        ♦ 4 0 | 6  0 0 | 4  0  0 0 | 1 * * *
         ox   .. xo&#x                     ♦ 2 2 | 1  4 1 | 0  2  2 0 | * 6 * *
         ..   ox3xo&#x                     ♦ 3 3 | 3  6 3 | 1  3  3 1 | * * 4 *
reduced( .x3/2.x3.o    )                   ♦ 0 4 | 0  0 6 | 0  0  0 4 | * * * 1

top of page