Acronym	ope, K-4.11 (alt: dytpuf)
Name	octahedron prism, vertex figure of rat, dyadic tegmipucofastegium, equatorial cross-section of tet-first dot
Segmentochoron display
Cross sections	©
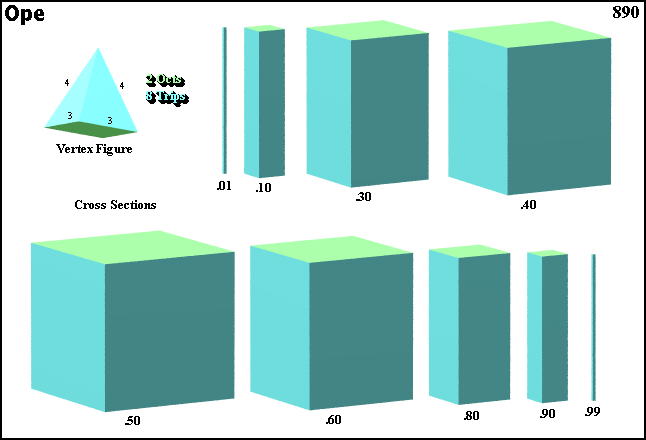Circumradius	sqrt(3)/2 = 0.866025
Lace city in approx. ASCII-art	x3o x3o -- x x3o (trip) o3x o3x -- x o3x (gyro trip) | | | +-- s2s3s (oct) +-------- s2s3s (oct)
Coordinates	(1/sqrt(2), 0, 0, 1/2)   & all permutations in all but last coord., all changes of sign
Volume	sqrt(2)/3 = 0.471405
General of army	(is itself convex)
Colonel of regiment	(is itself locally convex – uniform polychoral members: by cells: cube oct thah trip thahp 3 0 2 4 ope 0 2 0 8 )
Dual	cute
Dihedral angles	at {4} between trip and trip:   arccos(-1/3) = 109.471221° at {3} between oct and trip:   90°
Face vector	12, 30, 28, 10
Confer	more general: n-appip   n-tepuf   segmentochora: squippyp   general polytopal classes: Wythoffian polychora   segmentochora   bistratic lace towers   lace simplices   Hanner polytopes
External links

It should be mentioned that into ope a q-tet could be vertex-inscribed: within either base an opposite vertex-pair has distance q each; if those pairs would be chosen mutually orthogonal in either base, then the distance from such a vertex to the non-orthogonal one within that base clearly is x (an edge length) and the distance from that point to the opposite base too is x, thus resulting totally in q again. – In fact this best can be seen in the representation of ope as x o o || x x x || x o o where that q-tet is easily given by the alternate vertices of the equatorial cube. (An according tetradiminishing however necessarily yields q-edges in its hull.)

Incidence matrix according to Dynkin symbol

x x3o4o

. . . . | 12 ♦ 1  4 |  4  4 | 4 1
--------+----+------+-------+----
x . . . |  2 | 6  * |  4  0 | 4 0
. x . . |  2 | * 24 |  1  2 | 2 1
--------+----+------+-------+----
x x . . |  4 | 2  2 | 12  * | 2 0
. x3o . |  3 | 0  3 |  * 16 | 1 1
--------+----+------+-------+----
x x3o . ♦  6 | 3  6 |  3  2 | 8 *
. x3o4o ♦  6 | 0 12 |  0  8 | * 2

x x3o4/3o

. . .   . | 12 ♦ 1  4 |  4  4 | 4 1
----------+----+------+-------+----
x . .   . |  2 | 6  * |  4  0 | 4 0
. x .   . |  2 | * 24 |  1  2 | 2 1
----------+----+------+-------+----
x x .   . |  4 | 2  2 | 12  * | 2 0
. x3o   . |  3 | 0  3 |  * 16 | 1 1
----------+----+------+-------+----
x x3o   . ♦  6 | 3  6 |  3  2 | 8 *
. x3o4/3o ♦  6 | 0 12 |  0  8 | * 2

x x3/2o4o

. .   . . | 12 ♦ 1  4 |  4  4 | 4 1
----------+----+------+-------+----
x .   . . |  2 | 6  * |  4  0 | 4 0
. x   . . |  2 | * 24 |  1  2 | 2 1
----------+----+------+-------+----
x x   . . |  4 | 2  2 | 12  * | 2 0
. x3/2o . |  3 | 0  3 |  * 16 | 1 1
----------+----+------+-------+----
x x3/2o . ♦  6 | 3  6 |  3  2 | 8 *
. x3/2o4o ♦  6 | 0 12 |  0  8 | * 2

x x3/2o4/3o

. .   .   . | 12 ♦ 1  4 |  4  4 | 4 1
------------+----+------+-------+----
x .   .   . |  2 | 6  * |  4  0 | 4 0
. x   .   . |  2 | * 24 |  1  2 | 2 1
------------+----+------+-------+----
x x   .   . |  4 | 2  2 | 12  * | 2 0
. x3/2o   . |  3 | 0  3 |  * 16 | 1 1
------------+----+------+-------+----
x x3/2o   . ♦  6 | 3  6 |  3  2 | 8 *
. x3/2o4/3o ♦  6 | 0 12 |  0  8 | * 2

x o3x3o

. . . . | 12 ♦ 1  4 |  4 2 2 | 2 2 1
--------+----+------+--------+------
x . . . |  2 | 6  * |  4 0 0 | 2 2 0
. . x . |  2 | * 24 |  1 1 1 | 1 1 1
--------+----+------+--------+------
x . x . |  4 | 2  2 | 12 * * | 1 1 0
. o3x . |  3 | 0  3 |  * 8 * | 1 0 1
. . x3o |  3 | 0  3 |  * * 8 | 0 1 1
--------+----+------+--------+------
x o3x . ♦  6 | 3  6 |  3 2 0 | 4 * *
x . x3o ♦  6 | 3  6 |  3 0 2 | * 4 *
. o3x3o ♦  6 | 0 12 |  0 4 4 | * * 2

x o3x3/2o

. . .   . | 12 ♦ 1  4 |  4 2 2 | 2 2 1
----------+----+------+--------+------
x . .   . |  2 | 6  * |  4 0 0 | 2 2 0
. . x   . |  2 | * 24 |  1 1 1 | 1 1 1
----------+----+------+--------+------
x . x   . |  4 | 2  2 | 12 * * | 1 1 0
. o3x   . |  3 | 0  3 |  * 8 * | 1 0 1
. . x3/2o |  3 | 0  3 |  * * 8 | 0 1 1
----------+----+------+--------+------
x o3x   . ♦  6 | 3  6 |  3 2 0 | 4 * *
x . x3/2o ♦  6 | 3  6 |  3 0 2 | * 4 *
. o3x3/2o ♦  6 | 0 12 |  0 4 4 | * * 2

x o3/2x3/2o

. .   .   . | 12 ♦ 1  4 |  4 2 2 | 2 2 1
------------+----+------+--------+------
x .   .   . |  2 | 6  * |  4 0 0 | 2 2 0
. .   x   . |  2 | * 24 |  1 1 1 | 1 1 1
------------+----+------+--------+------
x .   x   . |  4 | 2  2 | 12 * * | 1 1 0
. o3/2x   . |  3 | 0  3 |  * 8 * | 1 0 1
. .   x3/2o |  3 | 0  3 |  * * 8 | 0 1 1
------------+----+------+--------+------
x o3/2x   . ♦  6 | 3  6 |  3 2 0 | 4 * *
x .   x3/2o ♦  6 | 3  6 |  3 0 2 | * 4 *
. o3/2x3/2o ♦  6 | 0 12 |  0 4 4 | * * 2

x s2s3s

. demi( . . . ) | 12 ♦ 1 1 1  2 | 1 1 1 2  3 | 1 1 3
----------------+----+----------+------------+------
.       s2s .   ♦  2 | 6 * *  * | 1 0 0 0  2 | 0 1 2
.       s 2 s   ♦  2 | * 6 *  * | 0 1 0 0  2 | 0 1 2
x demi( . . . ) |  2 | * * 6  * | 1 1 0 2  0 | 1 0 3
. sefa( . s3s ) |  2 | * * * 12 | 0 0 1 1  1 | 1 1 1
----------------+----+----------+------------+------
x       s2s .   |  4 | 2 0 2  0 | 3 * * *  * | 0 0 2
x       s 2 s   |  4 | 0 2 2  0 | * 3 * *  * | 0 0 2
.       . s3s   ♦  3 | 0 0 0  3 | * * 4 *  * | 1 1 0
x sefa( . s3s ) |  4 | 0 0 2  2 | * * * 6  * | 1 0 1
. sefa( s2s3s ) |  3 | 1 1 0  1 | * * * * 12 | 0 1 1
----------------+----+----------+------------+------
x       . s3s   ♦  6 | 0 0 3  6 | 0 0 2 3  0 | 2 * *
.       s2s3s   ♦  6 | 3 3 0  6 | 0 0 2 0  6 | * 2 *
x sefa( s2s3s ) ♦  6 | 2 2 3  2 | 1 1 0 1  2 | * * 6

x s2s6o

. demi( . . . ) | 12 ♦  2 1  2 | 2 1 2  3 | 1 1 3
----------------+----+---------+----------+------
.       s2s .   ♦  2 | 12 *  * | 1 0 0  2 | 0 1 2
x demi( . . . ) |  2 |  * 6  * | 2 0 2  0 | 1 0 3
. sefa( . s6o ) |  2 |  * * 12 | 0 1 1  1 | 1 1 1
----------------+----+---------+----------+------
x       s2s .   |  4 |  2 2  0 | 6 * *  * | 0 0 2
.       . s6o   ♦  3 |  0 0  3 | * 4 *  * | 1 1 0
x sefa( . s6o ) |  4 |  0 2  2 | * * 6  * | 1 0 1
. sefa( s2s6o ) |  3 |  2 0  1 | * * * 12 | 0 1 1
----------------+----+---------+----------+------
x       . s6o   ♦  6 |  0 3  6 | 0 2 3  0 | 2 * *
.       s2s6o   ♦  6 |  6 0  6 | 0 2 0  6 | * 2 *
x sefa( s2s6o ) ♦  6 |  4 3  2 | 2 0 1  2 | * * 6

xx3oo4oo&#x   → height = 1
(oct || oct)

o.3o.4o.    | 6 * ♦  4 1  0 | 4  4 0 | 1 4 0
.o3.o4.o    | * 6 ♦  0 1  4 | 0  4 4 | 0 4 1
------------+-----+---------+--------+------
x. .. ..    | 2 0 | 12 *  * | 2  1 0 | 1 2 0
oo3oo4oo&#x | 1 1 |  * 6  * | 0  4 0 | 0 4 0
.x .. ..    | 0 2 |  * * 12 | 0  1 2 | 0 2 1
------------+-----+---------+--------+------
x.3o. ..    | 3 0 |  3 0  0 | 8  * * | 1 1 0
xx .. ..&#x | 2 2 |  1 2  1 | * 12 * | 0 2 0
.x3.o ..    | 0 3 |  0 0  3 | *  * 8 | 0 1 1
------------+-----+---------+--------+------
x.3o.4o.    ♦ 6 0 | 12 0  0 | 8  0 0 | 1 * *
xx3oo ..&#x ♦ 3 3 |  3 3  3 | 1  3 1 | * 8 *
.x3.o4.o    ♦ 0 6 |  0 0 12 | 0  0 8 | * * 1

oo3xx3oo&#x   → height = 1
(oct || oct)

o.3o.3o.    | 6 * ♦  4 1  0 | 2 2  4 0 0 | 1 2 2 0
.o3.o3.o    | * 6 ♦  0 1  4 | 0 0  4 2 2 | 0 2 2 1
------------+-----+---------+------------+--------
.. x. ..    | 2 0 | 12 *  * | 1 1  1 0 0 | 1 1 1 0
oo3oo3oo&#x | 1 1 |  * 6  * | 0 0  4 0 0 | 0 2 2 0
.. .x ..    | 0 2 |  * * 12 | 0 0  1 1 1 | 0 1 1 1
------------+-----+---------+------------+--------
o.3x. ..    | 3 0 |  3 0  0 | 4 *  * * * | 1 1 0 0
.. x.3o.    | 3 0 |  3 0  0 | * 4  * * * | 1 0 1 0
.. xx ..&#x | 2 2 |  1 2  1 | * * 12 * * | 0 1 1 0
.o3.x ..    | 0 3 |  0 0  3 | * *  * 4 * | 0 1 0 1
.. .x3.o    | 0 3 |  0 0  3 | * *  * * 4 | 0 0 1 1
------------+-----+---------+------------+--------
o.3x.3o.    ♦ 6 0 | 12 0  0 | 4 4  0 0 0 | 1 * * *
oo3xx ..&#x ♦ 3 3 |  3 3  3 | 1 0  3 1 0 | * 4 * *
.. xx3oo&#x ♦ 3 3 |  3 3  3 | 0 1  3 0 1 | * * 4 *
.o3.x3.o    ♦ 0 6 |  0 0 12 | 0 0  0 4 4 | * * * 1

xx xo3ox&#x   → height = sqrt(2/3) = 0.816497
(trip || gyro trip)

o. o.3o.    | 6 * ♦ 1 2  2 0 0 | 2 1 2 2 1 0 0 | 1 2 1 1 0
.o .o3.o    | * 6 ♦ 0 0  2 1 2 | 0 0 2 1 2 2 1 | 0 1 2 1 1
------------+-----+------------+---------------+----------
x. .. ..    | 2 0 | 3 *  * * * | 2 0 2 0 0 0 0 | 1 2 1 0 0
.. x. ..    | 2 0 | * 6  * * * | 1 1 0 1 0 0 0 | 1 1 0 1 0
oo oo3oo&#x | 1 1 | * * 12 * * | 0 0 1 1 1 0 0 | 0 1 1 1 0
.x .. ..    | 0 2 | * *  * 3 * | 0 0 2 0 0 2 0 | 0 1 2 0 1
.. .. .x    | 0 2 | * *  * * 6 | 0 0 0 0 1 1 1 | 0 0 1 1 1
------------+-----+------------+---------------+----------
x. x. ..    | 4 0 | 2 2  0 0 0 | 3 * * * * * * | 1 1 0 0 0
.. x.3o.    | 3 0 | 0 3  0 0 0 | * 2 * * * * * | 1 0 0 1 0
xx .. ..&#x | 2 2 | 1 0  2 1 0 | * * 6 * * * * | 0 1 1 0 0
.. xo ..&#x | 2 1 | 0 1  2 0 0 | * * * 6 * * * | 0 1 0 1 0
.. .. ox&#x | 1 2 | 0 0  2 0 1 | * * * * 6 * * | 0 0 1 1 0
.x .. .x    | 0 4 | 0 0  0 2 2 | * * * * * 3 * | 0 0 1 0 1
.. .o3.x    | 0 3 | 0 0  0 0 3 | * * * * * * 2 | 0 0 0 1 1
------------+-----+------------+---------------+----------
x. x.3o.    ♦ 6 0 | 3 6  0 0 0 | 3 2 0 0 0 0 0 | 1 * * * *
xx xo ..&#x ♦ 4 2 | 2 2  4 1 0 | 1 0 2 2 0 0 0 | * 3 * * *
xx .. ox&#x ♦ 2 4 | 1 0  4 2 2 | 0 0 2 0 2 1 0 | * * 3 * *
.. xo3ox&#x ♦ 3 3 | 0 3  6 0 3 | 0 1 0 3 3 0 1 | * * * 2 *
.x .o3.x    ♦ 0 6 | 0 0  0 3 6 | 0 0 0 0 0 3 2 | * * * * 1

s2s3s || s2s3s   → height = 1
(oct || oct)

demi( . . . )                 | 6 * ♦ 1 1 2 1 0 0 0 | 1 3 1 1 2 0 0 | 1 1 3 0
                demi( . . . ) | * 6 ♦ 0 0 0 1 1 1 2 | 0 0 1 1 2 1 3 | 0 1 3 1
------------------------------+-----+---------------+---------------+--------
      s2s .                   ♦ 2 0 | 3 * * * * * * | 0 2 1 0 0 0 0 | 1 0 1 0
      s 2 s                   ♦ 2 0 | * 3 * * * * * | 0 2 0 1 0 0 0 | 1 0 1 0
sefa( . s3s )                 | 2 0 | * * 6 * * * * | 1 1 0 0 1 0 0 | 1 1 1 0
demi( . . . ) || demi( . . . ) | 1 1 | * * * 6 * * * | 0 0 1 1 2 0 0 | 0 1 3 0
                      s2s .   ♦ 0 2 | * * * * 3 * * | 0 0 1 0 0 0 2 | 0 0 2 1
                      s 2 s   ♦ 0 2 | * * * * * 3 * | 0 0 0 1 0 0 2 | 0 0 2 1
                sefa( . s3s ) | 0 2 | * * * * * * 6 | 0 0 0 0 1 1 1 | 0 1 1 1
------------------------------+-----+---------------+---------------+--------
      . s3s                   ♦ 3 0 | 0 0 3 0 0 0 0 | 2 * * * * * * | 1 1 0 0
sefa( s2s3s )                 | 3 0 | 1 1 1 0 0 0 0 | * 6 * * * * * | 1 0 1 0
      s2s .   ||       s2s .   | 2 2 | 1 0 0 2 1 0 0 | * * 3 * * * * | 0 0 2 0
      s 2 s   ||       s 2 s   | 2 2 | 0 1 0 2 0 1 0 | * * * 3 * * * | 0 0 2 0
sefa( . s3s ) || sefa( . s3s ) | 2 2 | 0 0 1 2 0 0 1 | * * * * 6 * * | 0 1 1 0
                      . s3s   ♦ 0 3 | 0 0 0 0 0 0 3 | * * * * * 2 * | 0 1 0 1
                sefa( s2s3s ) | 0 3 | 0 0 0 0 1 1 1 | * * * * * * 6 | 0 0 1 1
------------------------------+-----+---------------+---------------+--------
      s2s3s                   ♦ 6 0 | 3 3 6 0 0 0 0 | 2 6 0 0 0 0 0 | 1 * * *
      . s3s   ||       . s3s   ♦ 3 3 | 0 0 3 3 0 0 3 | 1 0 0 0 3 1 0 | * 2 * *
sefa( s2s3s ) || sefa( s2s3s ) ♦ 3 3 | 1 1 1 3 1 1 1 | 0 1 1 1 1 0 1 | * * 6 *
                      s2s3s   ♦ 0 6 | 0 0 0 0 n n 6 | 0 0 0 0 0 2 6 | * * * 1

s2s6o || s2s6o   → height = 1
(oct || oct:   triangular appip)

demi( . . . )                 | 6 * ♦ 2 2 1 0 0 | 1 3 2 2 0 0 | 1 1 3 0
                demi( . . . ) | * 6 ♦ 0 0 1 2 2 | 0 0 2 2 1 3 | 0 1 3 1
------------------------------+-----+-----------+-------------+--------
      s2s .                   ♦ 2 0 | 6 * * * * | 0 2 1 0 0 0 | 1 0 2 0
sefa( . s6o )                 | 2 0 | * 6 * * * | 1 1 0 1 0 0 | 1 1 1 0
demi( . . . ) || demi( . . . ) | 1 1 | * * 6 * * | 0 0 2 2 0 0 | 0 1 3 0
                      s2s .   ♦ 0 2 | * * * 6 * | 0 0 1 0 0 2 | 0 0 2 1
                sefa( . s6o ) | 0 2 | * * * * 6 | 0 0 0 1 1 1 | 0 1 1 1
------------------------------+-----+-----------+-------------+--------
      . s6o                   ♦ 3 0 | 0 3 0 0 0 | 2 * * * * * | 1 1 0 0
sefa( s2s6o )                 | 3 0 | 2 1 0 0 0 | * 6 * * * * | 1 0 1 0
      s2s .   ||       s2s .   | 2 2 | 1 0 2 1 0 | * * 6 * * * | 0 0 2 0
sefa( . s6o ) || sefa( . s6o ) | 2 2 | 0 1 2 0 1 | * * * 6 * * | 0 1 1 0
                      . s6o   ♦ 0 3 | 0 0 0 0 3 | * * * * 2 * | 0 1 0 1
                sefa( s2s6o ) | 0 3 | 0 0 0 2 1 | * * * * * 6 | 0 0 1 1
------------------------------+-----+-----------+-------------+--------
      s2s6o                   ♦ 6 0 | 6 6 0 0 0 | 2 6 0 0 0 0 | 1 * * *
      . s6o   ||       . s6o   ♦ 3 3 | 0 3 3 0 3 | 1 0 0 3 1 0 | * 2 * *
sefa( s2s6o ) || sefa( s2s6o ) ♦ 3 3 | 2 1 3 2 1 | 0 1 2 1 0 1 | * * 6 *
                      s2s6o   ♦ 0 6 | 0 0 0 6 6 | 0 0 0 0 2 6 | * * * 1

xxx oxo4ooo&#xt   → both heights = 1/sqrt(2) = 0.707107
(line || pseudo cube || line:   dyadic tepuf)

o.. o..4o..     | 2 * * ♦ 1 4 0 0 0 0 | 4 4 0 0 0 | 4 1 0
.o. .o.4.o.     | * 8 * ♦ 0 1 1 2 1 0 | 1 2 2 1 2 | 2 1 2
..o ..o4..o     | * * 2 ♦ 0 0 0 0 4 1 | 0 0 0 4 4 | 0 1 4
----------------+-------+-------------+-----------+------
x.. ... ...     | 2 0 0 | 1 * * * * * | 4 0 0 0 0 | 4 0 0
oo. oo.4oo.&#x  | 1 1 0 | * 8 * * * * | 1 2 0 0 0 | 2 1 0
.x. ... ...     | 0 2 0 | * * 4 * * * | 1 0 2 1 0 | 2 0 2
... .x. ...     | 0 2 0 | * * * 8 * * | 0 1 1 0 1 | 1 1 1
.oo .oo4.oo&#x  | 0 1 1 | * * * * 8 * | 0 0 0 1 2 | 0 1 2
..x ... ...     | 0 0 2 | * * * * * 1 | 0 0 0 4 0 | 0 0 4
----------------+-------+-------------+-----------+------
xx. ... ...&#x  | 2 2 0 | 1 2 1 0 0 0 | 4 * * * * | 2 0 0
... ox. ...&#x  | 1 2 0 | 0 2 0 1 0 0 | * 8 * * * | 1 1 0
.x. .x. ...     | 0 4 0 | 0 0 2 2 0 0 | * * 4 * * | 1 0 1
.xx ... ...&#x  | 0 2 2 | 0 0 1 0 2 1 | * * * 4 * | 0 0 2
... .xo ...&#x  | 0 2 1 | 0 0 0 1 2 0 | * * * * 8 | 0 1 1
----------------+-------+-------------+-----------+------
xx. ox. ...&#x  ♦ 2 4 0 | 1 4 2 2 0 0 | 2 2 1 0 0 | 4 * *
... oxo4ooo&#xt ♦ 1 4 1 | 0 4 0 4 4 0 | 0 4 0 0 4 | * 2 *
.xx .xo ...&#x  ♦ 0 4 2 | 0 0 2 2 4 1 | 0 0 1 2 2 | * * 4

or
o.. o..4o..     & | 4 * ♦ 1  4 0 0 | 4  4 0 | 4 1
.o. .o.4.o.       | * 8 ♦ 0  2 1 2 | 2  4 2 | 4 1
------------------+-----+----------+--------+----
x.. ... ...     & | 2 0 | 2  * * * | 4  0 0 | 4 0
oo. oo.4oo.&#x  & | 1 1 | * 16 * * | 1  2 0 | 2 1
.x. ... ...       | 0 2 | *  * 4 * | 2  0 2 | 4 0
... .x. ...       | 0 2 | *  * * 8 | 0  2 1 | 2 1
------------------+-----+----------+--------+----
xx. ... ...&#x  & | 2 2 | 1  2 1 0 | 8  * * | 2 0
... ox. ...&#x  & | 1 2 | 0  2 0 1 | * 16 * | 1 1
.x. .x. ...       | 0 4 | 0  0 2 2 | *  * 4 | 2 0
------------------+-----+----------+--------+----
xx. ox. ...&#x  & ♦ 2 4 | 1  4 2 2 | 2  2 1 | 8 *
... oxo4ooo&#xt   ♦ 2 4 | 0  8 0 4 | 0  8 0 | * 2

xxx oxo oxo&#xt   → both heights = 1/sqrt(2) = 0.707107
(line || pseudo cube || line:   dyadic tepuf)

o.. o.. o..     | 2 * * ♦ 1 4 0 0 0 0 0 | 4 2 2 0 0 0 0 0 | 2 2 1 0 0
.o. .o. .o.     | * 8 * ♦ 0 1 1 1 1 1 0 | 1 1 1 1 1 1 1 1 | 1 1 1 1 1
..o ..o ..o     | * * 2 ♦ 0 0 0 0 0 4 1 | 0 0 0 0 0 4 2 2 | 0 0 1 2 2
----------------+-------+---------------+-----------------+----------
x.. ... ...     | 2 0 0 | 1 * * * * * * | 4 0 0 0 0 0 0 0 | 2 2 0 0 0
oo. oo. oo.&#x  | 1 1 0 | * 8 * * * * * | 1 1 1 0 0 0 0 0 | 1 1 1 0 0
.x. ... ...     | 0 2 0 | * * 4 * * * * | 1 0 0 1 1 1 0 0 | 1 1 0 1 1
... .x. ...     | 0 2 0 | * * * 4 * * * | 0 1 0 1 0 0 1 0 | 1 0 1 1 0
... ... .x.     | 0 2 0 | * * * * 4 * * | 0 0 1 0 1 0 0 1 | 0 1 1 0 1
.oo .oo .oo&#x  | 0 1 1 | * * * * * 8 * | 0 0 0 0 0 1 1 1 | 0 0 1 1 1
..x ... ...     | 0 0 2 | * * * * * * 1 | 0 0 0 0 0 4 0 0 | 0 0 0 2 2
----------------+-------+---------------+-----------------+----------
xx. ... ...&#x  | 2 2 0 | 1 2 1 0 0 0 0 | 4 * * * * * * * | 1 1 0 0 0
... ox. ...&#x  | 1 2 0 | 0 2 0 1 0 0 0 | * 4 * * * * * * | 1 0 1 0 0
... ... ox.&#x  | 1 2 0 | 0 2 0 0 1 0 0 | * * 4 * * * * * | 0 1 1 0 0
.x. .x. ...     | 0 4 0 | 0 0 2 2 0 0 0 | * * * 2 * * * * | 1 0 0 1 0
.x. ... .x.     | 0 4 0 | 0 0 2 0 2 0 0 | * * * * 2 * * * | 0 1 0 0 1
.xx ... ...&#x  | 0 2 2 | 0 0 1 0 0 2 1 | * * * * * 4 * * | 0 0 0 1 1
... .xo ...&#x  | 0 2 1 | 0 0 0 1 0 2 0 | * * * * * * 4 * | 0 0 1 1 0
... ... .xo&#x  | 0 2 1 | 0 0 0 0 1 2 0 | * * * * * * * 4 | 0 0 1 0 1
----------------+-------+---------------+-----------------+----------
xx. ox. ...&#x  ♦ 2 4 0 | 1 4 2 2 0 0 0 | 2 2 0 1 0 0 0 0 | 2 * * * *
xx. ... ox.&#x  ♦ 2 4 0 | 1 4 2 0 2 0 0 | 2 0 2 0 1 0 0 0 | * 2 * * *
... oxo oxo&#xt ♦ 1 4 1 | 0 4 0 2 2 4 0 | 0 2 2 0 0 0 2 2 | * * 2 * *
.xx .xo ...&#x  ♦ 0 4 2 | 0 0 2 2 0 4 1 | 0 0 0 1 0 2 2 0 | * * * 2 *
.xx ... .xo&#x  ♦ 0 4 2 | 0 0 2 0 2 4 1 | 0 0 0 0 1 2 0 2 | * * * * 2

or
o.. o.. o..     & | 4 * ♦ 1  4 0 0 0 | 4 2 2 0 0 | 2 2 1
.o. .o. .o.       | * 8 ♦ 0  2 1 1 1 | 2 2 2 1 1 | 2 2 1
------------------+-----+------------+-----------+------
x.. ... ...     & | 2 0 | 2  * * * * | 4 0 0 0 0 | 2 2 0
oo. oo. oo.&#x  & | 1 1 | * 16 * * * | 1 1 1 0 0 | 1 1 1
.x. ... ...       | 0 2 | *  * 4 * * | 2 0 0 1 1 | 2 2 0
... .x. ...       | 0 2 | *  * * 4 * | 0 2 0 1 0 | 2 0 1
... ... .x.       | 0 2 | *  * * * 4 | 0 0 2 0 1 | 0 2 1
------------------+-----+------------+-----------+------
xx. ... ...&#x  & | 2 2 | 1  2 1 0 0 | 8 * * * * | 1 1 0
... ox. ...&#x  & | 1 2 | 0  2 0 1 0 | * 8 * * * | 1 0 1
... ... ox.&#x  & | 1 2 | 0  2 0 0 1 | * * 8 * * | 0 1 1
.x. .x. ...       | 0 4 | 0  0 2 2 0 | * * * 2 * | 2 0 0
.x. ... .x.       | 0 4 | 0  0 2 0 2 | * * * * 2 | 0 2 0
------------------+-----+------------+-----------+------
xx. ox. ...&#x  & ♦ 2 4 | 1  4 2 2 0 | 2 2 0 1 0 | 4 * *
xx. ... ox.&#x  & ♦ 2 4 | 1  4 2 0 2 | 2 0 2 0 1 | * 4 *
... oxo oxo&#xt   ♦ 2 4 | 0  8 0 2 2 | 0 4 4 0 0 | * * 2

oqo xox xxx&#xt   → both heights = 1/2
({4} || ortho pseudo (q,x)-{4} || {4})

o.. o.. o..     & | 8 * ♦ 1 1  2 1 0 | 1 2 2 2 1 | 1 2 2
.o. .o. .o.       | * 4 ♦ 0 0  4 0 1 | 0 2 2 4 0 | 1 2 2
------------------+-----+------------+-----------+------
... x.. ...     & | 2 0 | 4 *  * * * | 1 0 2 0 0 | 1 2 0
... ... x..     & | 2 0 | * 4  * * * | 1 0 0 2 1 | 0 2 2
oo. oo. oo.&#x  & | 1 1 | * * 16 * * | 0 1 1 1 0 | 1 1 1
o.o o.o o.o&#x    | 2 0 | * *  * 4 * | 0 2 0 0 1 | 1 0 2
... ... .x.       | 0 2 | * *  * * 2 | 0 0 0 4 0 | 0 2 2
------------------+-----+------------+-----------+------
... x.. x..     & | 4 0 | 2 2  0 0 0 | 2 * * * * | 0 2 0
ooo ooo ooo&#xt   | 2 1 | 0 0  2 1 0 | * 8 * * * | 1 0 1
... xo. ...&#x  & | 2 1 | 1 0  2 0 0 | * * 8 * * | 1 1 0
... ... xx.&#x  & | 2 2 | 0 1  2 0 1 | * * * 8 * | 0 1 1
... ... x.x&#x    | 4 0 | 0 2  0 2 0 | * * * * 2 | 0 0 2
------------------+-----+------------+-----------+------
oqo xox ...&#xt   ♦ 4 2 | 2 0  8 2 0 | 0 4 4 0 0 | 2 * *
... xo. xx.&#x  & ♦ 4 2 | 2 2  4 0 1 | 1 0 2 2 0 | * 4 *
... ... xxx&#x    ♦ 4 2 | 0 2  4 2 1 | 0 2 0 2 1 | * * 4

xxx qoo oqo ooq&#zx   → height = 0
(tegum sum of 3 ortho (q,x)-{4})

o.. o.. o.. o..     | 4 * * ♦ 1 2 2 0 0 0 | 2 2  4 0 | 4 1
.o. .o. .o. .o.     | * 4 * ♦ 0 2 0 1 2 0 | 2 0  4 2 | 4 1
..o ..o ..o ..o     | * * 4 ♦ 0 0 2 0 2 1 | 0 2  4 2 | 4 1
--------------------+-------+-------------+----------+----
x.. ... ... ...     | 2 0 0 | 2 * * * * * | 2 2  0 0 | 4 0
oo. oo. oo. oo.&#x  | 1 1 0 | * 8 * * * * | 1 0  2 0 | 2 1
o.o o.o o.o o.o&#x  | 1 0 1 | * * 8 * * * | 0 1  2 0 | 2 1
.x. ... ... ...     | 0 2 0 | * * * 2 * * | 2 0  0 2 | 4 0
.oo .oo .oo .oo&#x  | 0 1 1 | * * * * 8 * | 0 0  2 1 | 2 1
..x ... ... ...     | 0 0 2 | * * * * * 2 | 0 2  0 2 | 4 0
--------------------+-------+-------------+----------+----
xx. ... ... ...&#x  | 2 2 0 | 1 2 0 1 0 0 | 4 *  * * | 2 0
x.x ... ... ...&#x  | 2 0 2 | 1 0 2 0 0 1 | * 4  * * | 2 0
ooo ooo ooo ooo&#x  | 1 1 1 | 0 1 1 0 1 0 | * * 16 * | 1 1
.xx ... ... ...&#x  | 0 2 2 | 0 0 0 1 2 1 | * *  * 4 | 2 0
--------------------+-------+-------------+----------+----
xxx ... ... ...&#x  ♦ 2 2 2 | 1 2 2 1 2 1 | 1 1  2 1 | 8 *
... qoo oqo ooq&#zx ♦ 2 2 2 | 0 4 4 0 4 0 | 0 0  8 0 | * 2