expanded kaleido-facetings

Expanded Kaleido-Facetings

In February 2014 a noteworthy combination from

Wythoffian kaleidoscopical construction, allowing for seed point positions outside of the fundamental domain as well,
subsymmetrical "layer" decompositions – esp. in the sense of lace towers (...&#xt) or even in a co-hyperrealmic sense (...&#zx, i.e. tegum sums), and
(partial) Stott expansions

was brought up by W. Gevaert. In the sequel a vivid research for class members of according CRFs was initiated, which then provided several so far unknown "crown jewels".

Gevaert himself also elaborated some of the first known examples, but then he reduced to just outline his ideas and contribute to combinatorics. Quickfur, "student5", and Čtrnáct also found some further individual examples. A more systematical research with several more finds and esp. the concrete cell evaluation of all known cases then has been done by Klitzing. (Therefore the following content mostly is original work.)

For kaleidoscopical construction usually a seed point within the fundamental domain is used. Its reflection all over the mirror symmetry then constructs the vertex set of the to be designed polytope. Obviously an other such vertex outside the domain likewise could be used, again providing the same vertex set – but then other elements in the dimensions beyond. Generally these such derived polytopes then will be facetings of the former polytope. If esp. that point was taken to be a direct mirror image of that point within, then that edge, which is derived as the hull of these 2 points, gets just inverted.

If one wonders what these kaleido-faceted polytopes would look like in terms of their Dynkin diagram, then clearly some edges, i.e. node symbols which formerly had prograde unit size, now will have retrograde unite size. That is, some x just gets reflected into a (-x). But because faces, which stay within their face planes, keep their neighbouring vertices still being connected, the other edges accordingly will get elongated thereby by the amount of a vertex figure, i.e. by the corresponding shortchord.

Assume we start with any (sub)diagram x-n/m-y (where y is just any length edge, possibly zero), then by flipping that x into (-x) we elongate the neighbouring edge from size y into y+cos(π m/n)x. Moreover, if we start with some layered starting figure, then such an edge flip could be applied independently in any layer. We just have to check, that still any layer can be connected by unit-lacings to at least one of the other layers. For its converse cf. †).

Obviously retrograde edges would not be allowed in CRF polytopes. To that aim a corresponding Stott expansion will come in, which then adds one unit to the respective node position – uniformely within all layers. Sometimes longer edges also would occur within the symbols of individual layers. Here we have to check then that those "edges" become just false ones (pseudo edges), burried somewhere within. E.g. covered by inter-layer lacing elements. For its converse cf. ‡).

Besides of the former exclusions we still have to check for the regularity of all the polygonal faces (of the total figure).

One of the most common cases wrt. ‡) can already be filtered out a priori: When considering convex starting polytopes which become displayed as mere lace towers, i.e. when keeping the layer heights throughout all the transformations, then mixtures of prograde and retrograde edges at the same node would not be allowable. This is because we have to apply a Stott expansion to the retrograde edges, bringing these edges then back to zero size. But this same expansion would double up simultanuously the prograde edges at the same node. Generally speaking, an inner-layer edge of size u = 2x might be allowable, e.g. as the equator of an hexagon. But within the reach of the given preconditions the 2 adjoined "halves" would not be co-planar before the expansion, and so by mere parallel translation cannot become thereafter.

This same argument surely serves valid for full dimensional subsymmetries which are cartesian products, provided all transformations affect only one cartesian component, while the other keeps unchanged. (This then would be the generalization of unchanged heights.) Even changes in more than one component are compensated here, provided this change can be split into independent changes in either affected component each.

Wrt. mere lace towers we likewise have an a priori restriction: lacing triangles freely can be affected by edge reversals, so can squares only if both parallel edges are affected simultanuously, but any other 2D face can not. Nor could any face be elongated within its face plain by later partial Stott expansions, except of those which do respect the full symmetry of that polygon.

†) - Layers fall apart into subsets: at least one layer cannot be connected to none of the other ones by unit inter-layer lacings. Or dead ends will arise: vertices of at least one non-extremal layer wrt. some axial orientation do not allow for unit inter-lacings to any higher (or lower) vertex.
‡) - At least one non-unit layer edge survives at the outside.
°) - Asks for some non-regular polygonal faces.

3D EKF:

EKF of the icosahedron

subsymmetry o2o2o (1 derived CRF)
subsymmetry . o3o (1 derived CRF)
subsymmetry . o5o (1 derived CRF)

EKF of the small rhombicuboctahedron

subsymmetry o3o3o (3 derived Wythoffians)
subsymmetry o2o4o & . o4o (2 derived CRFs & 3 derived Wythoffians)
subsymmetry . o3o (none)

EKF of the cuboctahedron

subsymmetry o3o3o (4 derived Wythoffians)
subsymmetry o2o4o & . o4o (1 derived Wythoffian)
subsymmetry o2o2o (1 derived Wythoffian)
subsymmetry . o3o (1 derived Wythoffian)

4D EKF:

EKF of the icosahedral pyramid

subsymmetry . o2o2o (1 derived CRF)
subsymmetry . . o3o (1 derived CRF)
subsymmetry . . o5o (1 derived CRF)

EKF of the hexacosachoron

subsymmetry o2o3o5o & . o3o5o (13 derived CRFs)
subsymmetry o3o3o3o (8 derived CRFs)
subsymmetry o3o3o *b3o (5 derived CRFs)
subsymmetry o5o2o5o (2 derived CRFs)
subsymmetry o3o2o3o (4 derived CRFs)
subsymmetry . o3o3o (8 derived CRFs)
subsymmetry o2o2o2o (2 derived CRFs)

EKF of the icositetrachoron

subsymmetry o3o3o4o (4 derived CRFs & 7 derived Wythoffians)
subsymmetry o2o3o4o & . o3o4o (10 derived CRFs & 5 derived Wythoffians)
subsymmetry o3o3o *b3o (4 derived CRFs & 3 derived Wythoffians)
subsymmetry o4o2o4o (1 derived CRFs & 1 derived Wythoffians)
...

EKF of the hexadecachoron

subsymmetry o2o3o4o & . o3o4o (10 derived CRFs & 5 derived Wythoffians)
subsymmetry . o3o3o (10 derived CRFs & 2 derived Wythoffians)
subsymmetry o4o2o4o (5 derived CRFs & 3 derived Wythoffians)
subsymmetry o2o2o2o (3 derived CRFs & 1 derived Wythoffian)
...

EKF of the pentachoron

subsymmetry . o3o3o (8 derived CRFs & 3 derived Wythoffians)
...

EKF of the rectified pentachoron

subsymmetry . o3o3o (8 derived CRFs & 3 derived Wythoffians)
...

EKF of the small rhombated pentachoron

subsymmetry . o3o3o (2 derived CRFs & 2 derived Wythoffians)
...

EKF of the decachoron

subsymmetry . o3o3o (3 derived CRFs & 4 derived Wythoffians)
subsymmetry . o2o3o (2 derived Wythoffians)
...

EKF of the small prismatodecachoron

subsymmetry . o3o3o (2 derived CRFs & 2 derived Wythoffians)
subsymmetry . o2o3o (1 derived CRF)
...

EKF of the rectified hexacosachoron

subsymmetry o2o3o5o & . o3o5o (1 derived CRF)
subsymmetry o3o3o *b3o (1 derived CRF)
subsymmetry o5o2o5o (none)
subsymmetry o3o2o3o (none)
...

EKF of the small prismated icositetrachoron

subsymmetry o2o3o4o & . o3o4o (1 derived CRF)
subsymmetry o3o3o *b3o (4 derived CRFs & 3 derived Wythoffians)
...

EKF of the snub (dis)icositetrachoron

subsymmetry o3o3o *b3o (2 derived CRFs)
subsymmetry o2o2o2o (1 derived CRF)
...

EKF of the rectified tesseract

subsymmetry o2o3o4o & . o3o4o (4 derived CRFs & 3 derived Wythoffians)
subsymmetry . o3o3o (1 derived CRF & 2 derived Wythoffians)
...

EKF of the icosahedron (`x3o5o`)

©

in `o2o2o` subsymmetry (up)
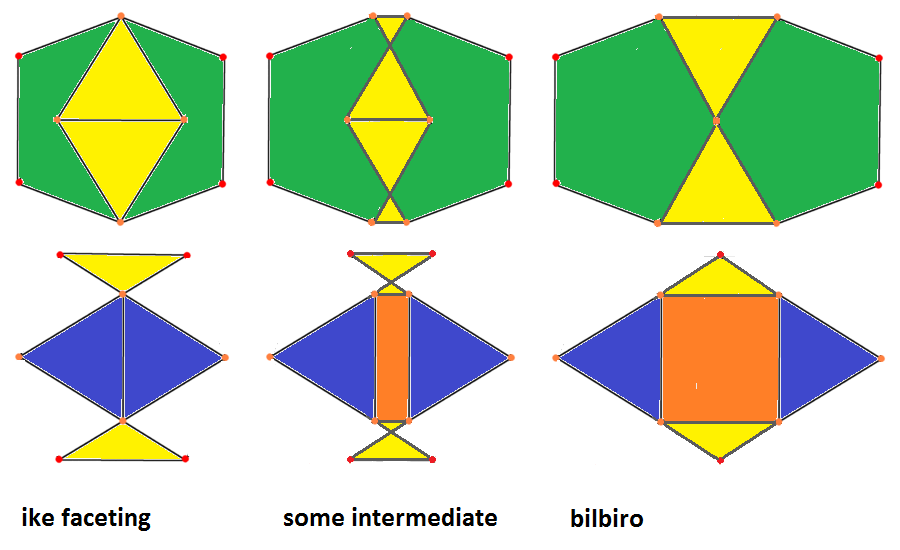
Representation:	xof 2 fxo 2 ofx &#zx (ike) = xofox 2 ofxfo &#xt
All layers & kaleido-facetings per layer:	A: x 2 f 2 o → A1: (-x) 2 f 2 o B: o 2 x 2 f → B2: o 2 (-x) 2 f C: f 2 o 2 x → C3: f 2 o 2 (-x)
A priori invalid combinations:	none
Other layer-combinations:	A1: (-x)of 2 fxo 2 ofx &#zx A1B2: (-x)of 2 f(-x)o 2 ofx &#zx → †) A1B2C3: (-x)of 2 f(-x)o 2 of(-x) &#zx → †)
Stott expansion: (derived potential CRFs)	oxF 2 fxo 2 ofx &#zx (bilbiro, J91) = oxFxo 2 ofxfo &#xt

in `. o3o` subsymmetry (up)
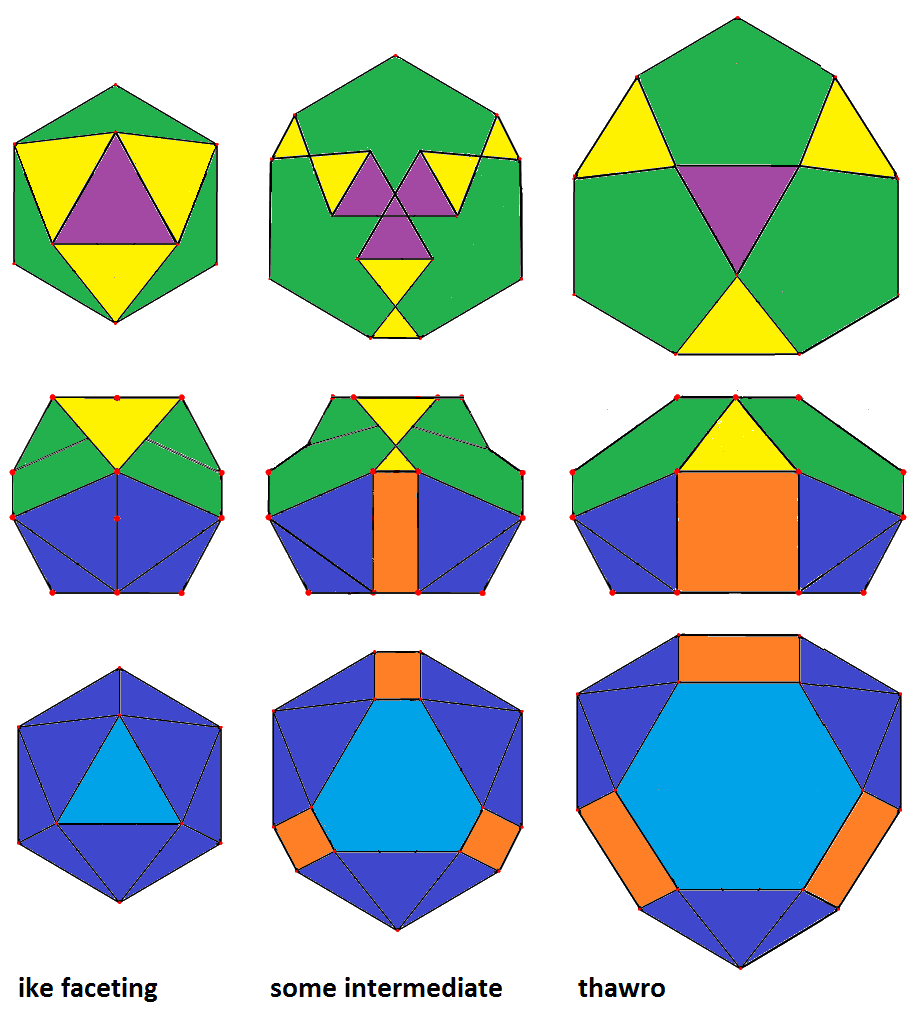
Representation:	xofo 3 ofox &#xt (ike)
All layers & kaleido-facetings per layer:	A: x 3 o → A1: (-x) 3 x B: o 3 f C: f 3 o D: o 3 x → D2: x 3 (-x)
A priori invalid combinations:	A1 + D2 → ‡) (u in A, u in D)
Other layer-combinations:	A1: (-x)ofo 3 xfox &#xt
Stott expansion: (derived potential CRFs)	oxFx 3 xfox &#xt (thawro, J92)

in `. o5o` subsymmetry (up)
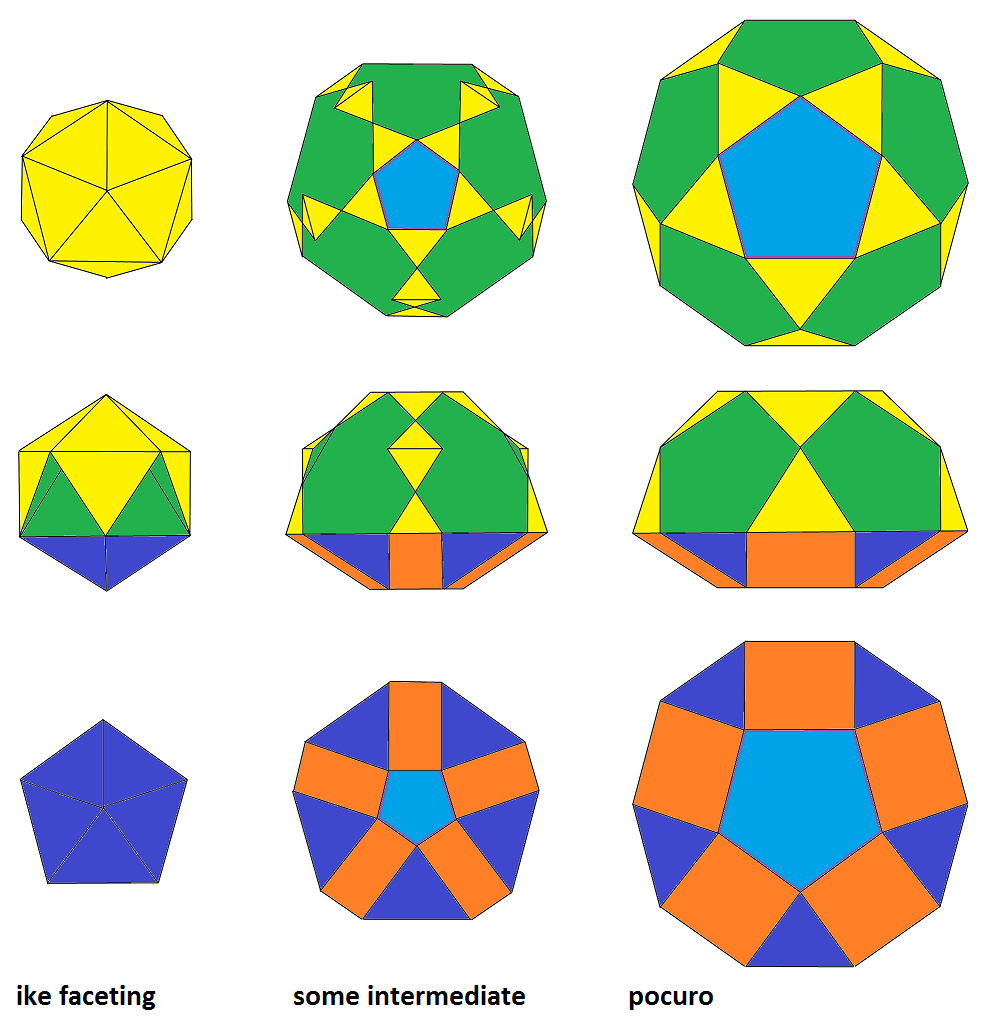
Representation:	oxoo 5 ooxo &#xt (ike)
All layers & kaleido-facetings per layer:	A: o 5 o B: x 5 o → B1: (-x) 5 f C: o 5 x → C2: f 5 (-x) D: o 5 o
A priori invalid combinations:	none
Other layer-combinations:	B1: o(-x)oo 5 ofxo &#xt B1C2: o(-x)fo 5 of(-x)o &#xt → †)
Stott expansion: (derived potential CRFs)	xoxx 5 ofxo &#xt (pocuro, J32) related: ..xx 5 ..xo &#xt (pecu, J5) related: xox. 5 ofx. &#xt (pero, J6)

EKF of the small rhombicuboctahedron (`x3o4x`)

©

in `o3o3o` subsymmetry (up)
Representation:	qo 3 xx 3 oq &#zx (sirco)
All layers & kaleido-facetings per layer:	A: q 3 x 3 o → A2: w 3 (-x) 3 x → A23: w 3 o 3 (-x) B: o 3 x 3 q → B2: x 3 (-x) 3 w → B21: (-x) 3 o 3 w
A priori invalid combinations:	A + B2 → ‡ (u in A) A2 + B → ‡ (u in B)
Other layer-combinations:	B21: q(-x) 3 xo 3 ow &#zx → †) A2B2: wx 3 (-x)(-x) 3 xw &#zx A2B21: w(-x) 3 (-x)o 3 xw &#zx → †) A23B21: w(-x) 3 oo 3 (-x)w &#zx → †)
Stott expansion: (derived potential CRFs & beyond)	1:-: wx 3 xx 3 oq &#zx → °) (asks for non-regular hexagons: wx .. oq &#zx) = non-Johnsonian (patex sirco)	(-2):-: qo 3 oo 3 oq &#zx = Wythoffian o3o4x (cube)
	13:-: wx 3 xx 3 xw &#zx = Wythoffian x3x4x (girco)	1(-2)3:-: wx 3 oo 3 xw &#zx = Wythoffian o3x4x (tic)
	2:A2B2: wx 3 oo 3 xw &#zx = Wythoffian o3x4x (tic)	(-1)2:A2B2: qo 3 oo 3 xw &#zx → °) (asks for non-regular hexagons: qo .. xw &#zx) = non-Johnsonian (patex cube)
	(-1)2(-3):A2B2: qo 3 oo 3 oq &#zx = Wythoffian o3o4x (cube)

in `o2o4o` subsymmetry (up)
Representation:	wx 2 xx 4 ox &#zx (sirco)
All layers & kaleido-facetings per layer:	A: w 2 x 4 o → A2: w 2 (-x) 4 q B: x 2 x 4 x → B1: (-x) 2 x 4 x → B12: (-x) 2 (-x) 4 w ↳ B13: (-x) 2 w 4 (-x) ↳ B2: x 2 (-x) 4 w → (B21 = B12) ↳ B3: x 2 w 4 (-x) → (B31 = B13)
A priori invalid combinations:	A + B2,B12 → ‡ (u in A) A2 → ‡ (q or w in extremal layer, i.e. A)
Other layer-combinations:	B1: w(-x) 2 xx 4 ox &#zx → †) B3: wx 2 xw 4 o(-x) &#zx B13: w(-x) 2 xw 4 o(-x) &#zx → †)
Stott expansion: (derived potential CRFs & beyond)	(-1):-: qo 2 xx 4 ox &#zx (squobcu, J28)	(-2):-: wx 2 oo 4 ox &#zx (esquidpy, J15)
	(-1)(-2):-: qo 2 oo 4 ox &#zx = Wythoffian x3o4o (oct)	3:B3: wx 2 xw 4 xo &#zx = Wythoffian o3x4x (tic)
	(-1)3:B3: qo 2 xw 4 xo &#zx → °) (asks for non-regular hexagons: qo 2 xw &#zx) = non-Johnsonian (pactic)	(-2)3:B3: wx 2 oq 4 xo &#zx → °) (asks for non-regular hexagons: wx 2 oq &#zx) = non-Johnsonian (pexco)
	(-1)(-2)3:B3: qo 2 oq 4 xo &#zx = Wythoffian o3x4o (co)
in `. o4o` subsymmetry (up)
Representation:	xxxx 4 oxxo &#xt (sirco) related: xxx. 4 oxx. &#xt (escu, J19) related: xx.. 4 ox.. &#x (squacu, J4) related: .xx. 4 .xx. &#x (op)
additional, not prismatically symmetric combinations of formers:	none, because A2 was ruled out already, and the possible combinations B1 + B3, B1 + B13, and B3 + B13 within the 2 medial layers B each would ask for u-edges there → ‡)

in `. o3o` subsymmetry (up)
Representation:	xxwoqo 3 oqowxx &#xt (sirco)
All layers & kaleido-facetings per layer:	A: x 3 o → A1: (-x) 3 x → A12: o 3 (-x) B: x 3 q → B1: (-x) 3 w C: w 3 o D: o 3 w E: q 3 x → E2: w 3 (-x) F: o 3 x → F2: x 3 (-x) → F21: (-x) 3 o
A priori invalid combinations:	A + B1,F21 → ‡ (u in A) A1 + B,E2,F2 → ‡ (u in A) A12 + E,F → ‡ (u in A) B + F21 → ‡ (u in F) B1 + F2 → ‡ (u in F) E + F2 → ‡ (u in F) E2 + F → ‡ (u in F)
Other layer-combinations:	E2F2 xxwowx 3 oqow(-x)(-x) &#xt A1B1F21 (-x)(-x)woq(-x) 3 xwowxo &#xt → †) A12B1E2F21 o(-x)wow(-x) 3 (-x)wow(-x)o &#xt → †)
Stott expansion: (derived potential CRFs & beyond)	1:E2F2: xxwowx 3 xwxQoo &#xt → °) (asks for non-unit edges DC, DE, DF) related: xxw.wx 3 xwx.oo &#xt → °) (asks for non-regular hexagons: ... xwx &#xt)

EKF of the cuboctahedron (`o3x4o`)

©

in `o3o3o` subsymmetry (up)
Representation:	x3o3x (co)
All layers & kaleido-facetings per layer:	A: x3o3x → A1: (-x)3 x 3 x → A12: o 3(-x)3 u ↳ A13: (-x)3 u 3(-x) ↳ A3: x 3 x 3(-x) → (A31 = A13) ↳ (A32 = A23)
A priori invalid combinations:	A12, A13 → ‡ (u in A)
Stott expansion: (derived potential CRFs)	(-1):-: o3o3x = Wythoffian (tet)	2:-: x3x3x = Wythoffian (toe)
	(-1)2:-: o3x3x = Wythoffian (tut)	(-1)2(-3):-: o3x3o = Wythoffian (oct)
	1:A1: o3x3x = Wythoffian (tut)	1(-2):A1: o3o3x = Wythoffian (tet)
	1(-3):A1: o3x3o = Wythoffian (oct)

in `o2o4o` subsymmetry (up)
Representation:	qo 2 xo 4 oq &#zx (co)
All layers & kaleido-facetings per layer:	A: q2x4o → A2: q 2(-x)4 q B: o2o4q
A priori invalid combinations:	A2 → ‡ (q in A)
Stott expansion: (derived potential CRFs & beyond)	1:-: wx 2 xo 4 oq &#zx → °) (asks for non-regular hexagons: wx .. oq &#zx) = non-Johnsonian (pexco)	3:-: qo 2 xo 4 xw &#zx → °) (asks for non-regular hexagons: qo .. xw &#zx) = non-Johnsonian (pactic)
Stott expansion: (derived potential CRFs & beyond)	13:-: wx 2 xo 4 xw &#zx = Wythoffian o3x4x (tic)
in `. o4o` subsymmetry (up)
Representation:	xox 4 oqo &#xt (co)
additional, not prismatically symmetric combinations of formers:	none, because A2 was disallowed and thus no independent changes in extremal layers A remain possible.

in `o2o2o` subsymmetry (up)
Representation:	qoq 2 qqo 2 oqq &#zx (co)
All layers & kaleido-facetings per layer:	A: q2q2o B: o2q2q C: q2o2q (As this representation does not show up (true / x-) edges within the layers, those thus cannot be inverted either. Therefore at most pure partial Stott expansions wrt. this subsymmetry remain possible.)
Stott expansion: (derived potential CRFs)	1:-: wxw 2 qqo 2 oqq &#zx → °) (asks for non-regular hexagons: wx .. oq &#zx) = non-Johnsonian (pexco)	12:-: wxw 2 wwx 2 oqq &#zx → °) (asks for non-regular hexagons: wx .. oq &#zx) = non-Johnsonian (pactic)
Stott expansion: (derived potential CRFs)	123:-: wxw 2 wwx 2 xww &#zx = Wythoffian o3x4x (tic)

in `. o3o` subsymmetry (up)
Representation:	xxo 3 oxx &#xt (co)
All layers & kaleido-facetings per layer:	A: x3o → A1: (-x)3x → A12: o3(-x) B: x3x → B1: (-x)3u ↳ B2: u3(-x) C: o3x → C2: x3(-x) → C21: (-x)3o
A priori invalid combinations:	A + B1,C21 → ‡ (u in A) A1 + B2,C2 → ‡ (u in A) A12 + B,C → ‡ (u in A) B + C2,C21 → ‡ (u in B) B1 + C2 → ‡ (u in C) B2 + C → ‡ (u in C)
Other layer-combinations:	C2 xxx 3 ox(-x) &#xt → †) B2C2 xux 3 o(-x)(-x) &#xt A1C21 (-x)x(-x) 3 xxo &#xt → †) A1B1C21 (-x)(-x)(-x) 3 xuo &#xt → †) A12B1C21 o(-x)(-x) 3 (-x)uo &#xt → †)
Stott expansion: (derived potential CRFs)	2:AB2C2: xux 3 xoo &#xt = Wythoffian o3x3x (tut)

EKF of the icosahedral pyramid (`ox3oo5oo&#x`)

©

Obviously here at most those subsymmetries can be applied, which do respect the possibilities of the base polyhedron, i.e. of the icosahedron (cf. above). As it turns out, all three types become positively applicable.

in `. o2o2o` subsymmetry (up)
Representation:	xof 2 fxo 2 ofx &#zx \|\| o2o2o (ikepy) = xofox 2 ofxfo &#xt \|\| o2o	©
All layers & kaleido-facetings per layer:	A: x 2 f 2 o → A1: (-x) 2 f 2 o B: o 2 x 2 f → B2: o 2 (-x) 2 f C: f 2 o 2 x → C3: f 2 o 2 (-x) D: o 2 o 2 o
A priori invalid combinations:	none
Other layer-combinations:	A1: (-x)of 2 fxo 2 ofx &#zx \|\| o2o2o A1B2: (-x)of 2 f(-x)o 2 ofx &#zx \|\| o2o2o → †) A1B2C3: (-x)of 2 f(-x)o 2 of(-x) &#zx \|\| o2o2o → †)
Stott expansion: (derived potential CRFs)	oxF 2 fxo 2 ofx &#zx \|\| x2o2o = oxFxo 2 ofxfo &#xt \|\| x2o = bilbiro \|\| line → CRF with cell list: 1 bilbiro (J91) 4 peppies (J2) 4 squippies (J1) 4 tets 2 trips

in `. . o3o` subsymmetry (up)
Representation:	xofo 3 ofox &#xt \|\| o3o (ikepy)	©
All layers & kaleido-facetings per layer:	A: x 3 o → A1: (-x) 3 x B: o 3 f C: f 3 o D: o 3 x → D2: x 3 (-x) E: o 3 o
A priori invalid combinations:	A1 + D2 → ‡) (u in A, u in D)
Other layer-combinations:	A1: (-x)ofo 3 xfox &#xt \|\| o3o
Stott expansion: (derived potential CRFs)	oxFx 3 xfox &#xt \|\| x3o = thawro \|\| {3} → CRF with cell list: 1 oct 3 peppies (J2) 3 squippies (J1) 9 tets 1 thawro (J92) 1 tricu (J3) 3 trips

in `. . o5o` subsymmetry (up)
Representation:	oxoo 5 ooxo &#xt \|\| o5o (ikepy)	©
All layers & kaleido-facetings per layer:	A: o 5 o B: x 5 o → B1: (-x) 5 f C: o 5 x → C2: f 5 (-x) D: o 5 o E: o 5 o
A priori invalid combinations:	none
Other layer-combinations:	B1: o(-x)oo 5 ofxo &#xt \|\| o5o B1C2: o(-x)fo 5 of(-x)o &#xt \|\| o5o → †)
Stott expansion: (derived potential CRFs)	xoxx 5 ofxo &#xt \|\| x5o = pocuro \|\| {5} → CRF with cell list: 5 peppies (J2) 2 pips 1 pocuro (J32) 10 squippies (J1) 5 tets 5 trips related: xox. 5 ofx. &#xt \|\| x5o = pero \|\| {5} → CRF (segmentochoron) with cell list: 1 pecu (J5) 5 peppies (J2) 1 pero (J6) 1 pip 10 squippies (J1) related: ..xx 5 ..xo &#x \|\| x5o = pecu \|\| {5} → CRF (segmentochoron) with cell list: 2 pecu (J5) 1 pip 5 tets 5 trips

EKF of the hexacosachoron (`x3o3o5o`)

©

in `o2o3o5o` subsymmetry (up)
Representation:	VFfxo 2 oxofo 3 oooox 5 ooxoo &#zx = oxofofoxo 3 ooooxoooo 5 ooxoooxoo &#xt (ex)
All layers & kaleido-facetings per layer:	A: V2o3o5o B: F2x3o5o → B2: F 2(-x)3 x 5 o → B23: F 2 o 3(-x)5 f C: f2o3o5x → C4: f 2 o 3 f 5(-x) D: x2f3o5o → D1: (-x)2 f 3 o 5 o E: o2o3x5o → E3: o 2 x 3(-x)5 f → E32: o 2(-x)3 o 5 f
A priori invalid combinations:	when component 1 (o2.3.5.) remains unchanged (no D1): B2 + E3 → ‡) (u in B, u in E) E32 + B → ‡) (u in B) B23 + E → ‡) (u in E) when component 2 (.2o3o5o) remains unchanged (neither B2, B23, C4, E3, E32): none As changes in (o2.3.5.) do not affect (.2o3o5o) and vice versa, the above exclusions remain valid too, when D1 is activ.
Other layer-combinations:	D1: VFf(-x)o 2 oxofo 3 oooox 5 ooxoo &#zx B2: VFfxo 2 o(-x)ofo 3 oxoox 5 ooxoo &#zx → †) B2E32: VFfxo 2 o(-x)of(-x) 3 oxooo 5 ooxof &#zx E3: VFfxo 2 oxofx 3 oooo(-x) 5 ooxof &#zx B23E3: VFfxo 2 ooofx 3 o(-x)oo(-x) 5 ofxof &#zx C4: VFfxo 2 oxofo 3 oofox 5 oo(-x)oo &#zx B2D1: VFf(-x)o 2 o(-x)ofo 3 oxoox 5 ooxoo &#zx B2D1E32: VFf(-x)o 2 o(-x)of(-x) 3 oxooo 5 ooxof &#zx → †) D1E3: VFf(-x)o 2 oxofx 3 oooo(-x) 5 ooxof &#zx B23D1E3: VFf(-x)o 2 ooofx 3 o(-x)oo(-x) 5 ofxof &#zx C4D1: VFf(-x)o 2 oxofo 3 oofox 5 oo(-x)oo &#zx B23E32: VFfxo 2 ooof(-x) 3 o(-x)ooo 5 ofxof &#zx → †) B2C4: VFfxo 2 o(-x)ofo 3 oxfox 5 oo(-x)oo &#zx B2C4E32: VFfxo 2 o(-x)of(-x) 3 oxfoo 5 oo(-x)of &#zx → †) C4E3: VFfxo 2 oxofx 3 oofo(-x) 5 oo(-x)of &#zx B23D1E32: VFf(-x)o 2 ooof(-x) 3 o(-x)ooo 5 ofxof &#zx → †) B2C4D1: VFf(-x)o 2 o(-x)ofo 3 oxfox 5 oo(-x)oo &#zx B2C4D1E32: VFf(-x)o 2 o(-x)of(-x) 3 oxfoo 5 oo(-x)of &#zx → †) C4D1E3: VFf(-x)o 2 oxofx 3 oofo(-x) 5 oo(-x)of &#zx → †) B23C4D1E3: VFf(-x)o 2 ooofx 3 o(-x)fo(-x) 5 of(-x)of &#zx → †) B23C4E32: VFfxo 2 ooof(-x) 3 o(-x)foo 5 of(-x)of &#zx → †) B23C4D1E32: VFf(-x)o 2 ooof(-x) 3 o(-x)foo 5 of(-x)of &#zx → †)
Stott expansion: (derived potential CRFs)	1:D1: BAFox 2 oxofo 3 oooox 5 ooxoo &#zx = oxoofooxo 3 oooxoxooo 5 ooxoooxoo &#xt (telex) → CRF with cell list: 24 ikes 60 squippies (J1) 180 tets 20 trips related: ..Fox 2 ..ofo 3 ..oox 5 ..xoo &#zx = ..oofoo.. 3 ..oxoxo.. 5 ..xooox.. &#xt → CRF with cell list: 2 does 24 gyepips (J11) 60 squippies (J1) 40 tets 20 trips related: ...ox 2 ...fo 3 ...ox 5 ...oo &#zx = ...ofo... 3 ...xox... 5 ...ooo... &#xt (twau iddip) → CRF with cell list: 2 ids 24 peppies (J2) 60 squippies (J1) 20 trips	2:B2E32: VFfxo 2 xoxFo 3 oxooo 5 ooxof &#zx = xoxFoFxox 3 oxoooooxo 5 ooxofoxoo &#xt → CRF with cell list: 30 bilbiroes (J91) 26 ikes 80 octs 60 squippies (J1) 40 tets related: ..fxo 2 ..xFo 3 ..ooo 5 ..xof &#zx = ..xFoFx.. 3 ..ooooo.. 5 ..xofox.. &#xt → CRF with cell list: 30 bilbiroes (J91) 24 peppies (J2) 2 srids 40 tets
	3:E3: VFfxo 2 oxofx 3 xxxxo 5 ooxof &#zx = oxofxfoxo 3 xxxxoxxxx 5 ooxofoxoo &#xt → CRF with cell list: 2 ids 30 ikes 40 octs 60 pips 180 squippies (J1) 180 tets 80 tricues (J3) 120 trips related: ..fxo 2 ..ofx 3 ..xxo 5 ..xof &#zx = ..ofxfo.. 3 ..xxoxx.. 5 ..xofox.. &#xt → CRF with cell list: 30 ikes 40 octs 24 pecues (J5) 12 pips 180 squippies (J1) 2 tids related: ..o.xfo.. 3 ..x.oxx.. 5 ..x.fox.. &#xt → CRF with cell list: 30 mibdies (J62) 40 octs 12 pecues (J5) 12 peroes (J6) 60 squippies (J1) 2 tids	3:B23E3: VFfxo 2 ooofx 3 xoxxo 5 ofxof &#zx = ooofxfooo 3 xoxxoxxox 5 ofxofoxfo &#xt → CRF with cell list: 2 ids 40 ikes 40 octs 12 pips 24 pocuroes (J32) 180 squippies (J1) 80 tets related: ..fxo 2 ..ofx 3 ..xxo 5 ..xof &#zx = ..ofxfo.. 3 ..xxoxx.. 5 ..xofox.. &#xt → CRF with cell list: 30 ikes 40 octs 24 pecues (J5) 12 pips 180 squippies (J1) 2 tids related: ..o.xfo.. 3 ..x.oxx.. 5 ..x.fox.. &#xt → CRF with cell list: 30 mibdies (J62) 40 octs 12 pecues (J5) 12 peroes (J6) 60 squippies (J1) 2 tids
	4:C4: VFfxo 2 oxofo 3 oofox 5 xxoxx &#zx = oxofofoxo 3 oofoxofoo 5 xxoxxxoxx &#xt → CRF with cell list: 2 does 40 ikes 60 pips 300 squippies (J1) 100 tets 120 trips related: .Ffxo 2 .xofo 3 .ofox 5 .xoxx &#zx = .xofofox. 3 .ofoxofo. 5 .xoxxxox. &#xt → CRF with cell list: 40 ikes 36 pips 300 squippies (J1) 2 srids 60 tets 60 trips related: .F.xo 2 .x.fo 3 .o.ox 5 .x.xx &#zx = .x.fof.x. 3 .o.oxo.o. 5 .x.xxx.x. &#xt → CRF with cell list: 96 pips 2 srids 40 teddies (J63) 60 tets 60 trips	12:B2D1: BAFox 2 xoxFx 3 oxoox 5 ooxoo &#zx = xoxxFxxox 3 oxoxoxoxo 5 ooxoooxoo &#xt → CRF with cell list: 48 gyepips (J11) 20 hips 2 ikes 80 octs 120 squippies (J1) 40 tricues (J3) 60 trips related: ...ox 2 ...Fx 3 ...ox 5 ...oo &#zx = ...xFx... 3 ...xox... 5 ...ooo... &#xt (twau tipe) → CRF with cell list: 20 hips 24 peppies (J2) 60 squippies (J1) 2 ties
	13:D1E3: BAFox 2 oxofx 3 xxxxo 5 ooxof &#zx = oxoxfxoxo 3 xxxoxoxxx 5 ooxfofxoo &#xt → CRF with cell list: 30 bilbiroes (J91) 2 ids 40 octs 24 pips 24 pocuroes (J32) 120 tets 80 tricues (J3) 20 trips related: ..Fox 2 ..ofx 3 ..xxo 5 ..xof &#zx = ..oxfxo.. 3 ..xoxox.. 5 ..xfofx.. &#xt → CRF with cell list: 30 bilbiroes (J91) 40 octs 24 peroes (J6) 2 tids 60 tets 20 trips	13:B23D1E3: BAFox 2 ooofx 3 xoxxo 5 ofxof &#zx = oooxfxooo 3 xoxoxoxox 5 ofxfofxfo &#xt → CRF with cell list: 30 bilbiroes (J91) 2 ids 40 octs 48 peroes (J6) 140 tets 20 trips related: ..Fox 2 ..ofx 3 ..xxo 5 ..xof &#zx = ..oxfxo.. 3 ..xoxox.. 5 ..xfofx.. &#xt → CRF with cell list: 30 bilbiroes (J91) 40 octs 24 peroes (J6) 2 tids 60 tets 20 trips
	14:C4D1: BAFox 2 oxofo 3 oofox 5 xxoxx &#zx = oxoofooxo 3 oofxoxfoo 5 xxoxxxoxx &#xt → CRF with cell list: 2 does 24 pips 24 pocuroes (J32) 120 squippies (J1) 40 teddies (J63) 40 tets 140 trips related: .AFox 2 .xofo 3 .ofox 5 .xoxx &#zx = .xoofoox. 3 .ofxoxfo. 5 .xoxxxox. &#xt → CRF with cell list: 24 pocuroes (J32) 120 squippies (J1) 2 srids 40 teddies (J63) 80 trips related: .xoo..... 3 .ofx..... 5 .xox..... &#xt → CRF with cell list: 12 peroes (J6) 30 squippies (J1) 1 srid 20 teddies (J63) 1 tid related: ...ox 2 ...fo 3 ...ox 5 ...xx &#zx = ...ofo... 3 ...xox... 5 ...xxx... &#xt (twau tiddip) → CRF with cell list: 24 pecues (J5) 60 squippies (J1) 2 tids 80 trips	24:B2C4: VFfxo 2 xoxFx 3 oxfox 5 xxoxx &#zx = xoxFxFxox 3 oxfoxofxo 5 xxoxxxoxx &#xt → CRF with cell list: 40 octs 12 pips 24 pocuroes (J32) 120 squippies (J1) 2 srids 120 tets 40 thawroes (J92) 180 trips related: .Ffxo 2 .oxFx 3 .xfox 5 .xoxx &#zx = .oxFxFxo. 3 .xfoxofx. 5 .xoxxxox. &#xt → CRF with cell list: 24 peroes (J6) 12 pips 120 squippies (J1) 120 tets 40 thawroes (J92) 2 tids 120 trips
	34:C4E3: VFfxo 2 oxofx 3 xxFxo 5 xxoxF &#zx = oxofxfoxo 3 xxFxoxFxx 5 xxoxFxoxx &#xt → CRF with cell list: 30 bilbiroes (J91) 60 dips 240 squippies (J1) 40 thawroes (J92) 2 tids 40 tricues (J3) 60 trips related: .Ffxo 2 .xofx 3 .xFxo 5 .xoxF &#zx = .xofxfox. 3 .xFxoxFx. 5 .xoxFxox. &#xt → CRF with cell list: 30 bilbiroes (J91) 36 dips 2 grids 240 squippies (J1) 40 thawroes (J92)	124:B2C4D1: BAFox 2 xoxFx 3 oxfox 5 xxoxx &#zx → ‡) (f in C)
in `. o3o5o` subsymmetry (up)
additional, not prismatically symmetric combinations of formers:	3:(B23)E3: oxo\|fxf\|ooo 3 xxx\|xox\|xox 5 oox\|ofo\|xfo &#xt → CRF with cell list: 2 ids 30 ikes 40 octs 36 pips 12 pocuroes (J32) 180 squippies (J1) 130 tets 40 tricues (J3) 60 trips	13:(B23)D1E3: oxo\|xfx\|ooo 3 xxx\|oxo\|xox 5 oox\|fof\|xfo &#xt → CRF with cell list: 30 bilbiroes (J91) 2 ids 40 octs 24 peroes (J6) 12 pips 12 pocuroes (J32) 130 tets 40 tricues (J3) 20 trips
using here node marks / (pseudo) edge lengths: `F=f+x, V=F+v=2f, A=F+x=f+2x, B=V+x=2f+x`

in `o3o3o3o` subsymmetry (up)
Representation:	xffoo 3 oxoof 3 fooxo 3 ooffx &#zx (ex)
All layers & kaleido-facetings per layer:	A: x3o3f3o → A1: (-x)3 x 3 f 3 o → A12: o 3(-x)3 F 3 o B: f3x3o3o → B2: F 3(-x)3 x 3 o → B23: F 3 o 3(-x)3 x → B234: F 3 o 3 o 3(-x) C: f3o3o3f D: o3o3x3f → D3: o 3 x 3(-x)3 F → D32: x 3(-x)3 o 3 F → D321: (-x)3 o 3 o 3 F E: o3f3o3x → E4: o 3 f 3 x 3(-x) → E43: o 3 F 3(-x)3 o
A priori invalid combinations:	none
Other layer-combinations:	A1: (-x)ffoo 3 xxoof 3 fooxo 3 ooffx &#zx D321: xff(-x)o 3 oxoof 3 foooo 3 oofFx &#zx → †) A1D321: (-x)ff(-x)o 3 xxoof 3 foooo 3 oofFx &#zx → †) A12: offoo 3 (-x)xoof 3 Fooxo 3 ooffx &#zx B2: xFfoo 3 o(-x)oof 3 fxoxo 3 ooffx &#zx D32: xffxo 3 oxo(-x)f 3 foooo 3 oofFx &#zx A12B2: oFfoo 3 (-x)(-x)oof 3 Fxoxo 3 ooffx &#zx B2D32: xFfxo 3 o(-x)o(-x)f 3 fxooo 3 oofFx &#zx A12D32: offxo 3 (-x)xo(-x)f 3 Foooo 3 oofFx &#zx → †) A12B2D32: oFfxo 3 (-x)(-x)o(-x)f 3 Fxooo 3 oofFx &#zx → †) A1B2: (-x)Ffoo 3 x(-x)oof 3 fxoxo 3 ooffx &#zx A1D32: (-x)ffxo 3 xxo(-x)f 3 foooo 3 oofFx &#zx B2D321: xFf(-x)o 3 o(-x)oof 3 fxooo 3 oofFx &#zx A12D321: off(-x)o 3 (-x)xoof 3 Foooo 3 oofFx &#zx → †) A1B2D32: (-x)Ffxo 3 x(-x)o(-x)f 3 fxooo 3 oofFx &#zx A1B2D321: (-x)Ff(-x)o 3 x(-x)oof 3 fxooo 3 oofFx &#zx → †) A12B2D321: oFf(-x)o 3 (-x)(-x)oof 3 Fxooo 3 oofFx &#zx → †) A1D3: (-x)ffoo 3 xxoxf 3 foo(-x)o 3 oofFx &#zx A1B23: (-x)Ffoo 3 xooof 3 f(-x)oxo 3 oxffx &#zx A1E43: (-x)ffoo 3 xxooF 3 foox(-x) 3 ooffo &#zx B23D321: xFf(-x)o 3 oooof 3 f(-x)ooo 3 oxfFx &#zx → †) D321E43: xff(-x)o 3 oxooF 3 fooo(-x) 3 oofFo &#zx → †) A1B23D3: (-x)Ffoo 3 xooxf 3 f(-x)o(-x)o 3 oxfFx &#zx A1D3E43: (-x)ffoo 3 xxoxF 3 foo(-x)(-x) 3 oofFo &#zx → †) A1B23D321: (-x)Ff(-x)o 3 xooof 3 f(-x)ooo 3 oxfFx &#zx → †) A1B23E43: (-x)Ffoo 3 xoooF 3 f(-x)ox(-x) 3 oxffo &#zx → †) A1D321E43: (-x)ff(-x)o 3 xxooF 3 fooo(-x) 3 oofFo &#zx → †) B23D321E43: xFf(-x)o 3 ooooF 3 f(-x)oo(-x) 3 oxfFo &#zx → †) A1B23D3E43: (-x)Ffoo 3 xooxF 3 f(-x)o(-x)(-x) 3 oxfFo &#zx → †) A1B23D321E43: (-x)Ff(-x)o 3 xoooF 3 f(-x)oo(-x) 3 oxfFo &#zx → †) A1E4: (-x)ffoo 3 xxoof 3 fooxx 3 ooff(-x) &#zx A1B234: (-x)Ffoo 3 xooof 3 fooxo 3 o(-x)ffx &#zx → †) B234D321: xFf(-x)o 3 oooof 3 foooo 3 o(-x)fFx &#zx → †) A1B234D321: (-x)Ff(-x)o 3 xooof 3 foooo 3 o(-x)fFx &#zx → †) A1B234E4: (-x)Ffoo 3 xooof 3 fooxx 3 o(-x)ff(-x) &#zx → †) A1B234D321E4: (-x)Ff(-x)o 3 xooof 3 fooox 3 o(-x)fF(-x) &#zx → †) B2D3: xFfoo 3 o(-x)oxf 3 fxo(-x)o 3 oofFx &#zx A12D3: offoo 3 (-x)xoxf 3 Foo(-x)o 3 oofFx &#zx → †) A12B23: oFfoo 3 (-x)ooof 3 F(-x)oxo 3 oxffx &#zx A12E43: offoo 3 (-x)xooF 3 Foox(-x) 3 ooffo &#zx B23D32: xFfxo 3 ooo(-x)f 3 f(-x)ooo 3 oxfFx &#zx A12B2D3: oFfoo 3 (-x)(-x)oxf 3 Fxo(-x)o 3 oofFx &#zx → †) A12B23D3: oFfoo 3 (-x)ooxf 3 F(-x)o(-x)o 3 oxfFx &#zx → †) A12B2E43: oFfoo 3 (-x)(-x)ooF 3 Fxox(-x) 3 ooffo &#zx → †) A12B23D32: oFfxo 3 (-x)oo(-x)f 3 F(-x)ooo 3 oxfFx &#zx → †) A12B2E43: oFfoo 3 (-x)(-x)ooF 3 Fxox(-x) 3 ooffo &#zx → †) A12B23E43: oFfoo 3 (-x)oooF 3 F(-x)ox(-x) 3 oxffo &#zx → †) A12B2D3E43: oFfoo 3 (-x)(-x)oxF 3 Fxo(-x)(-x) 3 oofFo &#zx → †) A12B23D3E43: oFfoo 3 (-x)ooxF 3 F(-x)o(-x)(-x) 3 oxfFo &#zx → †) A12B23D32E43: oFfxo 3 (-x)oo(-x)F 3 F(-x)oo(-x) 3 oxfFo &#zx → †) A1B2D3: (-x)Ffoo 3 x(-x)oxf 3 fxo(-x)o 3 oofFx &#zx A1B23D32: (-x)Ffxo 3 xoo(-x)f 3 f(-x)ooo 3 oxfFx &#zx A1B2E43: (-x)Ffoo 3 x(-x)ooF 3 fxox(-x) 3 ooffo &#zx → †) A1D32E43: (-x)ffxo 3 xxo(-x)F 3 fooo(-x) 3 oofFo &#zx → †) A12B23D321: oFf(-x)o 3 (-x)ooof 3 F(-x)ooo 3 oxfFx &#zx → †) A12D321E43: off(-x)o 3 (-x)xooF 3 Fooo(-x) 3 oofFo &#zx → †) B2D321E43: xFf(-x)o 3 o(-x)ooF 3 fxoo(-x) 3 oofFo &#zx → †) A1B2D3E43: (-x)Ffoo 3 x(-x)oxF 3 fxo(-x)(-x) 3 oofFo &#zx → †) A1B2D32E43: (-x)Ffxo 3 x(-x)o(-x)F 3 fxoo(-x) 3 oofFo &#zx → †) A1B2D321E43: (-x)Ff(-x)o 3 x(-x)ooF 3 fxoo(-x) 3 oofFo &#zx → †) A1B23D32E43: (-x)Ffxo 3 xoo(-x)F 3 f(-x)oo(-x) 3 oxfFo &#zx → †) A12B2D321E43: oFf(-x)o 3 (-x)(-x)ooF 3 Fxoo(-x) 3 oofFo &#zx → †) A12B23D321E43: oFf(-x)o 3 (-x)oooF 3 F(-x)oo(-x) 3 oxfFo &#zx → †) A1B2E4: (-x)Ffoo 3 x(-x)oof 3 fxoxx 3 ooff(-x) &#zx A1B234D32: (-x)Ffxo 3 xoo(-x)f 3 foooo 3 o(-x)fFx &#zx → †) A1D32E4: (-x)ffxo 3 xxo(-x)f 3 fooox 3 oofF(-x) &#zx B2D321E4: xFf(-x)o 3 o(-x)oof 3 fxoox 3 oofF(-x) &#zx → †) A12B234D321: oFf(-x)o 3 (-x)ooof 3 Foooo 3 o(-x)fFx &#zx → †) A12D321E4: off(-x)o 3 (-x)xoof 3 Fooox 3 oofF(-x) &#zx → †) A1B2D32E4: (-x)Ffxo 3 x(-x)o(-x)f 3 fxoox 3 oofF(-x) &#zx → †) A1B2D321E4: (-x)Ff(-x)o 3 x(-x)oof 3 fxoox 3 oofF(-x) &#zx → †) A12B2D321E4 oFf(-x)o 3 (-x)(-x)oof 3 Fxoox 3 oofF(-x) &#zx → †) A1B234D32E4: (-x)Ffxo 3 xoo(-x)f 3 fooox 3 o(-x)fF(-x) &#zx → †) A12B234D321E4: oFf(-x)o 3 (-x)ooof 3 Fooox 3 o(-x)fF(-x) &#zx → †) A1B2D3E4: (-x)Ffoo 3 x(-x)oxf 3 fxo(-x)x 3 oofF(-x) &#zx → †) A1B23D32E4: (-x)Ffxo 3 xoo(-x)f 3 f(-x)oox 3 oxfF(-x) &#zx → †) A1B234D32E43: (-x)Ffxo 3 xoo(-x)F 3 fooo(-x) 3 o(-x)fFo &#zx → †) A12B234D321E43: oFf(-x)o 3 (-x)oooF 3 Fooo(-x) 3 o(-x)fFo &#zx → †)
Stott expansion: (derived potential CRFs)	1:A1: oFFxx 3 xxoof 3 fooxo 3 ooffx &#zx → CRF with cell list: 5 coes 30 ikes 20 octs 90 squippies (J1) 125 tets 40 trips related: oF.xx 3 xx.of 3 fo.xo 3 oo.fx &#zx → CRF with cell list: 5 coes 30 mibdies (J62) 20 octs 90 squippies (J1) 20 teddies (J63) 25 tets 40 trips	2:A12: offoo 3 ouxxF 3 Fooxo 3 ooffx &#zx → ‡) (u in B)
	2:B2: xFfoo 3 xoxxF 3 fxoxo 3 ooffx &#zx → CRF with cell list: 20 ikes 25 octs 60 squippies (J1) 270 tets 40 tricues (J3) 60 trips 5 tuts	2:D32: xffxo 3 oxo(-x)f 3 foooo 3 oofFx &#zx → ‡) (u in B)
	2:A12B2: oFfoo 3 ooxxF 3 Fxoxo 3 ooffx &#zx → CRF with cell list: 30 bilbiroes (J91) 25 octs 20 teddies (J63) 80 tets 20 tricues (J3) 5 tuts	12:A12B2: xAFxx 3 ooxxF 3 Fxoxo 3 ooffx &#zx → CRF with cell list: 30 bilbiroes (J91) 25 octs 30 pips 20 teddies (J63) 60 tets 5 toes 40 tricues (J3) 40 trips
	2:B2D32: xFfxo 3 xoxoF 3 fxooo 3 oofFx &#zx → CRF with cell list: 20 ikes 25 octs 60 squippies (J1) 55 tets 20 thawroes (J92)	12:A1B2: oAFxx 3 uoxxF 3 fxoxo 3 ooffx &#zx → ‡) (u in A)
	12:A1D32: oFFux 3 uuxoF 3 foooo 3 oofFx &#zx → ‡) (u in A, u in B, u in D)	12: B2D321: uAFox 3 xoxxF 3 fxooo 3 oofFx &#zx → ‡) (u in A)
	12:A1B2D32: oAFux 3 uoxoF 3 fxooo 3 oofFx &#zx → ‡) (u in A, u in D)	13:A1D3: oFFxx 3 xxoxf 3 Fxxox 3 oofFx &#zx → CRF with cell list: 10 hips 20 octs 30 mibdies (J62) 90 squippies (J1) 20 thawroes (J92) 40 tricues (J3) 90 trips 10 tuts
	13:A1B23: oAFxx 3 xooof 3 Foxux 3 oxffx &#zx → ‡) (u in D)	13:A1E43: oFFxx 3 xxooF 3 Fxxuo 3 ooffo &#zx → ‡) (u in D)
	13:A1B23D3: oAFxx 3 xooxf 3 Foxox 3 oxfFx &#zx → ‡) (f in C)	14:A1E4: oFFxx 3 xxoof 3 fooxx 3 xxFFo &#zx → CRF with cell list: 60 bilbiroes (J91) 10 coes 40 octs 70 tets 20 trips
	23:A12E43: offoo 3 ouxxA 3 Axxuo 3 ooffo &#zx → ‡) (u in B, u in D)	23:B2D3: xFfoo 3 xoxuF 3 Fuxox 3 oofFx &#zx → ‡) (u in B, u in D)
	23:A12B23: oFfoo 3 oxxxF 3 Aoxux 3 oxffx &#zx → ‡) (u in D)	23:B23D32: xFfxo 3 xxxoF 3 Foxxx 3 oxfFx &#zx → CRF with cell list: 10 coes 60 pips 30 tets 40 thawroes (J92) 40 tricues (J3)
	123:A1B2D3: oAFxx 3 uoxuF 3 Fuxox 3 oofFx &#zx → ‡) (u in A, u in B, u in D)	123:A1B23D32: oAFux 3 uxxoF 3 Foxxx 3 oxfFx &#zx → ‡) (u in A, u in D)
	124:A1B2E4: oAFxx 3 uoxxF 3 fxoxx 3 xxFFo &#zx → ‡) (u in A)	124:A1D32E4: oFFux 3 uuxoF 3 fooox 3 xxFAo &#zx → ‡) (u in A, u in B, u in D)
using here node marks / (pseudo) edge lengths: `F=f+x, V=F+v=2f, A=F+x=f+2x, B=V+x=2f+x`

in `o3o3o *b3o` subsymmetry (up)
Representation:	foxo 3 ooof 3 xfoo *b3 oxfo &#zx (ex) with cyclical layer symmetry: A(134) → B(341) → C(413) → A(134)
All layers & kaleido-facetings per layer:	A: f3o3x b3o → A1: f 3 x 3(-x)b3 o → A12: F 3(-x)3 o b3 x → A123: F 3 o 3 o b3(-x) B: o3o3f b3x → B1: o 3 x 3 f b3(-x) → B12: x 3(-x)3 F b3 o → B123: (-x)3 o 3 F b3 o C: x3o3o b3f → C1: (-x)3 x 3 o b3 f → C12: o 3(-x)3 x b3 F → C123: o 3 o 3(-x)b3 F D: o3f3o *b3o
A priori invalid combinations:	none
Other layer-combinations:	C1: fo(-x)o 3 ooxf 3 xfoo b3 oxfo &#zx B123: f(-x)xo 3 ooof 3 xFoo b3 oofo &#zx → †) B123C1: f(-x)(-x)o 3 ooxf 3 xFoo b3 oofo &#zx → †) A12: Foxo 3 (-x)oof 3 ofoo b3 xxfo &#zx A12B12: Fxxo 3 (-x)(-x)of 3 oFoo b3 xofo &#zx → †) A12B12C12: Fxoo 3 (-x)(-x)(-x)f 3 oFxo b3 xoFo &#zx → †) A12C1: Fo(-x)o 3 (-x)oxf 3 ofoo b3 xxfo &#zx → †) A12B123: F(-x)xo 3 (-x)oof 3 oFoo b3 xofo &#zx → †) A12B12C1: Fx(-x)o 3 (-x)(-x)xf 3 oFoo b3 xofo &#zx → †) A12B123C1: F(-x)(-x)o 3 (-x)oxf 3 oFoo b3 xofo &#zx → †) A1C1: fo(-x)o 3 xoxf 3 (-x)foo b3 oxfo &#zx A1B123: f(-x)xo 3 xoof 3 (-x)Foo b3 oofo &#zx → †) B123C123: f(-x)oo 3 ooof 3 xF(-x)o b3 ooFo &#zx → †) A1B123C1: f(-x)(-x)o 3 xoxf 3 (-x)Foo b3 oofo &#zx → †) A1B123C123: f(-x)oo 3 xoof 3 (-x)F(-x)o b3 ooFo &#zx → †) A1B12C1: fx(-x)o 3 x(-x)xf 3 (-x)Foo b3 oofo &#zx → †) A1B123C12: f(-x)oo 3 xo(-x)f 3 (-x)Fxo b3 ooFo &#zx → †) A12B123C123: F(-x)oo 3 (-x)oof 3 oF(-x)o b3 xoFo &#zx → †) A1B1C1: fo(-x)o 3 xxxf 3 (-x)foo b3 o(-x)fo &#zx A123B123C123: F(-x)oo 3 ooof 3 oF(-x)o b3 (-x)oFo &#zx → †)
Stott expansion: (derived potential CRFs)	2:0: foxo 3 xxxF 3 xfoo b3 oxfo &#zx (icau prissi) → CRF with cell list: 480 tets 96 tricues (J3) 96 trips 24 tuts related: fox. 3 xxx. 3 xfo. b3 oxf. &#zx (prissi) → CRF with cell list: 24 ikes 96 tricues (J3) 96 trips 24 tuts	1:C1: Fxox 3 ooxf 3 xfoo b3 oxfo &#zx (icau pretasto) → CRF with cell list: 8 coes 32 ikes 40 octs 96 squippies (J1) 136 tets 48 trips related: Fxo. 3 oox. 3 xfo. b3 oxf. &#zx (pretasto) → CRF with cell list: 24 bilbiroes (J91) 8 coes 40 octs 32 teddies (J63) 40 tets
	2:A12: Foxo 3 oxxF 3 ofoo *b3 xxfo &#zx → CRF with cell list: 136 tets 32 thawroes (J92) 32 tricues (J3) 16 tuts	23:A12: Foxo 3 oxxF 3 xFxx *b3 xxfo &#zx → CRF with cell list: 8 coes 48 pips 96 tets 32 thawroes (J92) 8 toes 32 tricues (J3) 48 trips 8 tuts
	13:A1C1: Fxox 3 xoxf 3 oFxx *b3 oxfo &#zx → CRF with cell list: 8 coes 40 octs 96 squippies (J1) 32 teddies (J63) 32 thawroes (J92) 96 trips 8 tuts	134:A1B1C1: Fxox 3 xxxf 3 oFxx *b3 xoFx &#zx → ‡) (f in D)
using here node marks / (pseudo) edge lengths: `F=f+x`

in `o5o2o5o` subsymmetry (up)
Representation:	xfooxo 5 xofxoo 2 oxofox 5 ooxofx &#zx (ex) with layer symmetry: A(1234),B(1234),C(1234),D(1234),E(1234),F(1234) ↔ A(2143),C(2143),B(2143),E(2143),D(2143),F(2143) and cycle: A(1234),B(1234),C(1234),D(1234),E(1234),F(1234) → F(3421),D(3421),E(3421),C(3421),B(3421),A(3421) → A(2143),C(2143),B(2143),E(2143),D(2143),F(2143) → F(4312),E(4312),D(4312),B(4312),C(4312),A(4312) → A(1234),B(1234),C(1234),D(1234),E(1234),F(1234)
All layers & kaleido-facetings per layer:	A: x5x o5o → A1: (-x)5 F o 5 o or A2: F 5(-x) o 5 o B: f5o x5o → B3: f 5 o (-x)5 f C: o5f o5x → C4: o 5 f f 5(-x) D: o5x f5o → D2: f 5(-x) f 5 o E: x5o o5f → E1: (-x)5 f o 5 f F: o5o x5x → F3: o 5 o (-x)5 F or F4: o 5 o F 5(-x)
A priori invalid combinations:	when component 1 (o5o2.5.) remains unchanged (neither A1, A2, D2, E1): B3 + neither F3 nor F4 → ‡) (u in F) C4 + neither F3 nor F4 → ‡) (u in F) F3 + no B3 → ‡) (u in B) F4 + no C4 → ‡) (u in C) when component 2 (.5.2o5o) remains unchanged (neither B3, C4, F3, F4): E1 + neither A1 nor A2 → ‡) (u in A) D2 + neither A1 nor A2 → ‡) (u in A) A1 + no E1 → ‡) (u in E) A2 + no D2 → ‡) (u in D) As changes in (o5o2.5.) do not affect (.5.2o5o) and vice versa, the above exclusions become valid generally.
Other layer-combinations:	A1E1: (-x)foo(-x)o 5 Fofxfo 2 oxofox 5 ooxofx &#zx A1D2E1: (-x)fof(-x)o 5 Fof(-x)fo 2 oxofox 5 ooxofx &#zx A1B3E1F3: (-x)foo(-x)o 5 Fofxfo 2 o(-x)ofo(-x) 5 ofxofF &#zx A1B3D2E1F3: (-x)fof(-x)o 5 Fof(-x)fo 2 o(-x)ofo(-x) 5 ofxofF &#zx → †) A2B3D2E1F3: Ffof(-x)o 5 (-x)of(-x)fo 2 o(-x)ofo(-x) 5 ofxofF &#zx → †) A1B3C4D2E1F3: (-x)fof(-x)o 5 Fof(-x)fo 2 o(-x)ffo(-x) 5 of(-x)ofF &#zx → †)
Stott expansion: (derived potential CRFs)	-:0: xfooxo 5 xofxoo 2 oxofox 5 ooxofx &#zx → regular (ex itself) with cell list: 600 tets related: xfoo.o 5 xofx.o 2 oxof.x 5 ooxo.x &#zx → CRF with cell list: 25 mibdies (J62) 225 tets related: .foo.o 5 .ofx.o 2 .xof.x 5 .oxo.x &#zx → CRF with cell list: 25 mibdies (J62) 10 paps 75 tets related: .foox. 5 .ofxo. 2 .xofo. 5 .oxof. &#zx → uniform (gap) with cell list: 20 paps 300 tets	1:A1E1: oFxxox 5 Fofxfo 2 oxofox 5 ooxofx &#zx → CRF with cell list: 10 gyepips (J11) 25 ikes 10 pips 150 squippies (J1) 75 tets 50 trips related: .Fxxox 5 .ofxfo 2 .xofox 5 .oxofx &#zx → CRF with cell list: 10 paps 15 pips 25 ikes 75 tets 50 trips 125 squippies (J1) related: oFxx.x 5 Fofx.o 2 oxof.x 5 ooxo.x &#zx → CRF with cell list: 10 gyepips (J11) 25 mibdies (J62) 35 pips 25 squippies (J1) 75 tets 50 trips related: .Fxx.x 5 .ofx.o 2 .xof.x 5 .oxo.x &#zx → CRF with cell list: 25 mibdies (J62) 10 paps 40 pips 75 tets 50 trips
Stott expansion: (derived potential CRFs)	12:A1D2E1: oFxFox 5 AxFoFx 2 oxofox 5 ooxofx &#zx → CRF with cell list: 50 bilbiroes (J91) 10 dips 10 gyepips (J11) 5 pips 75 squippies (J1) related: .FxFox 5 .xFoFx 2 .xofox 5 .oxofx &#zx → CRF with cell list: 50 bilbiroes (J91) 10 dips 10 paps 10 pips 50 squippies (J1)	13:A1B3E1F3: oFxxox 5 Fofxfo 2 xoxFxo 5 ofxofF &#zx → ‡) (f in B)
using here node marks / (pseudo) edge lengths: `F=f+x, A=F+x=f+2x`

in `o3o2o3o` subsymmetry (up)
Representation:	fFoxffooxo 3 foFfxofxoo 2 oxofofxFof 3 ooxofxfoFf &#zx (ex) with layer symmetry: A(1234),B(1234),C(1234),D(1234),E(1234),F(1234),G(1234),H(1234),I(1234),J(1234) ↔ A(2143),C(2143),B(2143),E(2143),D(2143),G(2143),F(2143),I(2143),H(2143),J(2143) and cycle: A(1234),B(1234),C(1234),D(1234),E(1234),F(1234),G(1234),H(1234),I(1234),J(1234) → J(3421),H(3421),I(3421),G(3421),F(3421),D(3421),E(3421),C(3421),B(3421),A(3421) → A(2143),C(2143),B(2143),E(2143),D(2143),G(2143),F(2143),I(2143),H(2143),J(2143) → J(4312),I(4312),H(4312),F(4312),G(4312),E(4312),D(4312),B(4312),C(4312),A(4312) → A(1234),B(1234),C(1234),D(1234),E(1234),F(1234),G(1234),H(1234),I(1234),J(1234)
All layers & kaleido-facetings per layer:	A: f3f o3o B: F3o x3o → B3: F 3 o (-x)3 x → B34: F 3 o o 3(-x) C: o3F o3x → C4: o 3 F x 3(-x) → C43: o 3 F (-x)3 o D: x3f f3o → D1: (-x)3 F f 3 o E: f3x o3f → E2: F 3(-x) o 3 f F: f3o f3x → F4: f 3 o F 3(-x) G: o3f x3f → G3: o 3 f (-x)3 F H: o3x F3o → H2: x 3(-x) F 3 o → H21: (-x)3 o F 3 o I: x3o o3F → I1: (-x)3 x o 3 F → I12: o 3(-x) o 3 F J: o3o f3f
A priori invalid combinations:	when component 1 (o3o2.3.) remains unchanged (neither D1, E2, H2, H21, I1, I12): B3 + C4 → ‡) (u in B, u in C) B3 + F4 → ‡) (u in B) B3 + no G3 → ‡) (u in G) B34 + neither C4 nor C43 → ‡) (u in C) B34 + no F4 → ‡) (u in F) C4 + no F4 → ‡) (u in F) C4 + G3 → ‡) (u in C) C43 + neither B3 nor B34 → ‡) (u in B) C43 + no G3 → ‡) (u in G) F4 + neither C4 nor C43 → ‡) (u in C) G3 + neither B3 nor B34 → ‡) (u in B) when component 2 (.3.2o3o) remains unchanged (neither B3, B34, C4, C43, F4, G3): D1 + H2 → ‡) (u in H) D1 + neither I1 nor I12 → ‡) (u in I) E2 + neither H2 nor H21 → ‡) (u in H) E2 + I1 → ‡) (u in I) H2 + no E2 → ‡) (u in E) H2 + I1 → ‡) (u in H, u in I) H21 + no D1 → ‡) (u in D) H21 + neither I1 nor I12 → ‡) (u in I) I1 + no D1 → ‡) (u in D) I12 + no E2 → ‡) (u in E) I12 + neither H2 nor H21 → ‡) (u in H) As changes in (o3o2.3.) do not affect (.3.2o3o) and vice versa, the above exclusions become valid generally.
Other layer-combinations:	D1I1: fFo(-x)ffoo(-x)o 3 foFFxofxxo 2 oxofofxFof 3 ooxofxfoFf &#zx D1H21I1: fFo(-x)ffo(-x)(-x)o 3 foFFxofoxo 2 oxofofxFof 3 ooxofxfoFf &#zx D1E2H21I12: fFo(-x)Ffo(-x)oo 3 foFF(-x)ofo(-x)o 2 oxofofxFof 3 ooxofxfoFf &#zx B3D1G3I1: fFo(-x)ffoo(-x)o 3 foFFxofxxo 2 o(-x)ofof(-x)Fof 3 oxxofxFoFf &#zx B3C43D1G3I1: fFo(-x)ffoo(-x)o 3 foFFxofxxo 2 o(-x)(-x)fof(-x)Fof 3 oxoofxFoFf &#zx B3D1G3H21I1: fFo(-x)ffo(-x)(-x)o 3 foFFxofoxo 2 o(-x)ofof(-x)Fof 3 oxxofxFoFf &#zx B3C43D1G3H21I1: fFo(-x)ffo(-x)(-x)o 3 foFFxofoxo 2 o(-x)(-x)fof(-x)Fof 3 oxoofxFoFf &#zx → †) B3D1E2G3H21I12: fFo(-x)Ffo(-x)oo 3 foFF(-x)ofo(-x)o 2 o(-x)ofof(-x)Fof 3 oxxofxFoFf &#zx B3C43D1E2G3H21I12: fFo(-x)Ffo(-x)oo 3 foFF(-x)ofo(-x)o 2 o(-x)(-x)fof(-x)Fof 3 oxoofxFoFf &#zx → †) B34C43D1E2F4G3H21I12: fFo(-x)Ffo(-x)oo 3 foFF(-x)ofo(-x)o 2 oo(-x)foF(-x)Fof 3 o(-x)oof(-x)FoFf &#zx → †)
Stott expansion: (derived potential CRFs)	1:D1I1: FAxoFFxxox 3 foFFxofxxo 2 oxofofxFof 3 ooxofxfoFf &#zx → CRF with cell list: 27 ikes 6 octs 72 squippies (J1) 138 tets 6 tricues (J3) 30 trips related: FAxoFFxxo. 3 foFFxofxx. 2 oxofofxFo. 3 ooxofxfoF. &#zx → CRF with cell list: 18 ikes 9 mibdies (J62) 54 squippies (J1) 84 tets 6 thawroes (J92) 12 trips related: .AxoFFxxo. 3 .oFFxofxx. 2 .xofofxFo. 3 .oxofxfoF. &#zx → CRF with cell list: 18 gyepips (J11) 9 mibdies (J62) 54 squippies (J1) 6 teddies (J63) 54 tets 6 thawroes (J92) 12 trips	1:D1H21I1: FAxoFFxoox 3 foFFxofoxo 2 oxofofxFof 3 ooxofxfoFf &#zx → CRF with cell list: 9 bilbiroes (J91) 18 gyepips (J11) 9 ikes 54 squippies (J1) 87 tets 12 trips related: .AxoFFxoox 3 .oFFxofoxo 2 .xofofxFof 3 .oxofxfoFf &#zx → CRF with cell list: 9 bilbiroes (J91) 9 ikes 6 octs 18 paps 54 squippies (J1) 6 teddies (J63) 51 tets 12 trips
	12:D1E2H21I12: FAxoAFxoxx 3 FxAAoxFxox 2 oxofofxFof 3 ooxofxfoFf &#zx → CRF with cell list: 18 bilbiroes (J91) 18 pips 54 squippies (J1) 36 teddies (J63) 12 tets 12 tricues (J3) 24 trips	13:B3D1G3I1: FAxoFFxxox 3 foFFxofxxo 2 xoxFxFoAxF 3 oxxofxFoFf &#zx → CRF with cell list: 27 bilbiroes (J91) 3 hips 12 octs 9 mibdies (J62) 54 squippies (J1) 18 teddies (J63) 36 tets 12 tricues (J3) 30 trips
	13:B3C43D1G3I1: FAxoFFxxox 3 foFFxofxxo 2 xooFxFoAxF 3 oxoofxFoFf &#zx → †) (dead end at D)	13:B3D1G3H21I1: FAxoFFxoox 3 foFFxofoxo 2 xoxFxFoAxF 3 oxxofxFoFf &#xz → †) (dead end at D)
	123:B3D1E2G3H21I12: FAxoAFxoxx 3 FxAAoxFxox 2 xoxFxFoAxF 3 oxxofxFoFf &#zx → †) (dead end at D)
using here node marks / (pseudo) edge lengths: `F=f+x, A=F+x=f+2x`

in `. o3o3o` subsymmetry (up)
Representation:	xoo\|fox\|Ffo\|ofx\|ofo 3 oof\|oxf\|ooo\|fxo\|foo 3 ofo\|xfo\|ofF\|xof\|oox &#xt (ex)
All layers & kaleido-facetings per layer:	A: x3o3o → A1: (-x)3 x 3 o → A12: o 3(-x)3 x → A123: o 3 o 3(-x) B: o3o3f C: o3f3o D: f3o3x → D3: f 3 x 3(-x) → D32: F 3(-x)3 o E: o3x3f → E2: x 3(-x)3 F → E21: (-x)3 o 3 F F: x3f3o → F1: (-x)3 F 3 o G: F3o3o H: f3o3f g: o3o3F f: o3f3x → f3: o 3 F 3(-x) etc. antisymmetrically
A priori invalid combinations:	A1 + D32 → ‡) (u in A) A1 + E2 → ‡) (u in A, u in E) A1 + no F1 → ‡) (u in F) A1 + e2 → ‡) (u in A) A1 + d12 → ‡) (u in A) A1 + neither d1 nor d12 → ‡) (u in d) A1 + a32 → ‡) (u in A, u in a) A12 + D3 → ‡) (u in A, u in D) A12 + d1 → ‡) (u in A, u in d) A12 + neither E2 nor E21 → ‡) (u in E) A12 + f3 → ‡) (u in A) A12 + e23 → ‡) (u in A) A12 + neither e2 nor e23 → ‡) (u in e) A12 + a3 → ‡) (u in A, u in a) A123 + neither D3 nor D32 → ‡) (u in D) A123 + no f3 → ‡) (u in f) A123 + e2 → ‡) (u in e) A123 + neither a3, a32, a321 → ‡) (u in a) D3 + E2 → ‡) (u in D) D3 + no f3 → ‡) (u in f) D3 + e2 → ‡) (u in D, u in e) D3 + d12 → ‡) (u in D) D3 + a32 → ‡) (u in D, u in a) D3 + neither a3, a32, a321 → ‡) (u in a) D32 + neither E2 nor E21 → ‡) (u in E) D32 + neither e2 nor e23 → ‡) (u in e) D32 + d1 → ‡) (u in d) D32 + a3 → ‡) (u in a) E2 + F1 → ‡) (u in E) E2 + neither e2 nor e23 → ‡) (u in e) E2 + d1 → ‡) (u in E, u in d)	E2 + a3 → ‡) (u in E) E2 + a321 → ‡) (u in E) E21 + neither A1, A12, A123 → ‡) (u in A) E21 + no F1 → ‡) (u in F) E21 + neither d1 nor d12 → ‡) (u in d) E21 + a32 → ‡) (u in a) F1 + neither A1, A12, A123 → ‡) (u in A) F1 + neither d1 nor d12 → ‡) (u in d) F1 + a32 → ‡) (u in a) f3 + neither D3 nor D32 → ‡) (u in D) f3 + e2 → ‡) (u in e) f3 + neither a3, a32, a321 → ‡) (u in a) e2 + neither E2 nor E21 → ‡) (u in E) e2 + d1 → ‡) (u in d) e2 + a3 → ‡) (u in e, u in a) e23 + neither D3 nor D32 → ‡) (u in D) e23 + no f3 → ‡) (u in f) e23 + neither a3, a32, a321 → ‡) (u in a) d1 + neither A1, A12, A123 → ‡) (u in A) d1 + no F1 → ‡) (u in F) d1 + a32 → ‡) (u in d, u in a) d12 + neither E2 nor E21 → ‡) (u in E) d12 + neither e2 nor e23 → ‡) (u in e) d12 + a3 → ‡) (u in a) a3 + neither D3 nor D32 → ‡) (u in D) a3 + no f3 → ‡) (u in f) a32 + neither E2 nor E21 → ‡) (u in E) a32 + neither e2 nor e23 → ‡) (u in e) a321 + neither A1, A12, A123 → ‡) (u in A) a321 + no F1 → ‡) (u in F) a321 + neither d1 nor d12 → ‡) (u in d)
Other layer-combinations:	A1F1d1: (-x)oo\|fo(-x)\|Ffo\|of(-x)\|ofo 3 xof\|oxF\|ooo\|fxx\|foo 3 ofo\|xfo\|ofF\|xof\|oox &#xt A1E21F1d1: (-x)oo\|f(-x)(-x)\|Ffo\|of(-x)\|ofo 3 xof\|ooF\|ooo\|fxx\|foo 3 ofo\|xFo\|ofF\|xof\|oox &#xt A1F1d1a321: (-x)oo\|fo(-x)\|Ffo\|of(-x)\|of(-x) 3 xof\|oxF\|ooo\|fxx\|foo 3 ofo\|xfo\|ofF\|xof\|ooo &#xt → †) A1E21F1d1a321: (-x)oo\|f(-x)(-x)\|Ffo\|of(-x)\|of(-x) 3 xof\|ooF\|ooo\|fxx\|foo 3 ofo\|xFo\|ofF\|xof\|ooo &#xt → †) E2e2: xoo\|fxx\|Ffo\|oFx\|ofo 3 oof\|o(-x)f\|ooo\|f(-x)o\|foo 3 ofo\|xFo\|ofF\|xxf\|oox &#xt A12E2e2: ooo\|fxx\|Ffo\|oFx\|ofo 3 (-x)of\|o(-x)f\|ooo\|f(-x)o\|foo 3 xfo\|xFo\|ofF\|xxf\|oox &#xt D32E2e2: xoo\|Fxx\|Ffo\|oFx\|ofo 3 oof\|(-x)(-x)f\|ooo\|f(-x)o\|foo 3 ofo\|oFo\|ofF\|xxf\|oox &#xt A12D32E2e2: ooo\|Fxx\|Ffo\|oFx\|ofo 3 (-x)of\|(-x)(-x)f\|ooo\|f(-x)o\|foo 3 xfo\|oFo\|ofF\|xxf\|oox &#xt → †) (dead end at D) A12E2e2d12: ooo\|fxx\|Ffo\|oFo\|ofo 3 (-x)of\|o(-x)f\|ooo\|f(-x)(-x)\|foo 3 xfo\|xFo\|ofF\|xxF\|oox &#xt A12E2e2a32: ooo\|fxx\|Ffo\|oFx\|ofx 3 (-x)of\|o(-x)f\|ooo\|f(-x)o\|fo(-x) 3 xfo\|xFo\|ofF\|xxf\|ooo &#xt D32E2e2d12: xoo\|Fxx\|Ffo\|oFo\|ofo 3 oof\|(-x)(-x)f\|ooo\|f(-x)(-x)\|foo 3 ofo\|oFo\|ofF\|xxF\|oox &#xt A12D32E2e2d12: ooo\|Fxx\|Ffo\|oFo\|ofo 3 (-x)of\|(-x)(-x)f\|ooo\|f(-x)(-x)\|foo 3 xfo\|oFo\|ofF\|xxF\|oox &#xt → †) (dead end at D) A12D32E2e2a32: ooo\|Fxx\|Ffo\|oFx\|ofx 3 (-x)of\|(-x)(-x)f\|ooo\|f(-x)o\|fo(-x) 3 xfo\|oFo\|ofF\|xxf\|ooo &#xt → †) (dead end at D) A12D32E2e2d12a32: ooo\|Fxx\|Ffo\|oFo\|ofx 3 (-x)of\|(-x)(-x)f\|ooo\|f(-x)(-x)\|fo(-x) 3 xfo\|oFo\|ofF\|xxF\|ooo &#xt → †) (dead end at D) A12E21F1e2d12: ooo\|f(-x)(-x)\|Ffo\|oFo\|ofo 3 (-x)of\|ooF\|ooo\|f(-x)(-x)\|foo 3 xfo\|xFo\|ofF\|xxF\|oox &#xt A12D32E21F1e2d12: ooo\|F(-x)(-x)\|Ffo\|oFo\|ofo 3 (-x)of\|(-x)oF\|ooo\|f(-x)(-x)\|foo 3 xfo\|oFo\|ofF\|xxF\|oox &#xt → †) (dead end at D) A12E21F1e2d12a321: ooo\|f(-x)(-x)\|Ffo\|oFo\|of(-x) 3 (-x)of\|ooF\|ooo\|f(-x)(-x)\|foo 3 xfo\|xFo\|ofF\|xxF\|ooo &#xt → †) A12D32E21F1e2d12a321: ooo\|F(-x)(-x)\|Ffo\|oFo\|of(-x) 3 (-x)of\|(-x)oF\|ooo\|f(-x)(-x)\|foo 3 xfo\|oFo\|ofF\|xxF\|ooo &#xt → †) A1D3F1f3d1a3: (-x)oo\|fo(-x)\|Ffo\|of(-x)\|ofo 3 xof\|xxF\|ooo\|Fxx\|fox 3 ofo\|(-x)fo\|ofF\|(-x)of\|oo(-x) &#xt A1D3F1f3d1a321: (-x)oo\|fo(-x)\|Ffo\|of(-x)\|of(-x) 3 xof\|xxF\|ooo\|Fxx\|foo 3 ofo\|(-x)fo\|ofF\|(-x)of\|ooo &#xt → †) A123D3F1f3d1a321: ooo\|fo(-x)\|Ffo\|of(-x)\|of(-x) 3 oof\|xxF\|ooo\|Fxx\|foo 3 (-x)fo\|(-x)fo\|ofF\|(-x)of\|ooo &#xt → †) A1D3E21F1f3d1a3: (-x)oo\|f(-x)(-x)\|Ffo\|of(-x)\|ofo 3 xof\|xoF\|ooo\|Fxx\|fox 3 ofo\|(-x)Fo\|ofF\|(-x)of\|oo(-x) &#xt A1D3E21F1f3d1a321: (-x)oo\|f(-x)(-x)\|Ffo\|of(-x)\|of(-x) 3 xof\|xoF\|ooo\|Fxx\|foo 3 ofo\|(-x)Fo\|ofF\|(-x)of\|ooo &#xt → †) A123D3E21F1f3d1a321: ooo\|f(-x)(-x)\|Ffo\|of(-x)\|of(-x) 3 oof\|xoF\|ooo\|Fxx\|foo 3 (-x)fo\|(-x)Fo\|ofF\|(-x)of\|ooo &#xt → †) A1D3F1f3e23d1a321: (-x)oo\|fo(-x)\|Ffo\|oF(-x)\|of(-x) 3 xof\|xxF\|ooo\|Fox\|foo 3 ofo\|(-x)fo\|ofF\|(-x)(-x)f\|ooo &#xt → †) A1D3E21F1f3e23d1a3: (-x)oo\|f(-x)(-x)\|Ffo\|oF(-x)\|ofo 3 xof\|xoF\|ooo\|Fox\|fox 3 ofo\|(-x)Fo\|ofF\|(-x)(-x)f\|oo(-x) &#xt A1D3E21F1f3e23d1a321: (-x)oo\|f(-x)(-x)\|Ffo\|oF(-x)\|of(-x) 3 xof\|xoF\|ooo\|Fox\|foo 3 ofo\|(-x)Fo\|ofF\|(-x)(-x)f\|ooo &#xt → †) A123D3E21F1f3e23d1a321: ooo\|f(-x)(-x)\|Ffo\|oF(-x)\|of(-x) 3 oof\|xoF\|ooo\|Fox\|foo 3 (-x)fo\|(-x)Fo\|ofF\|(-x)(-x)f\|ooo &#xt → †) A123D32E21F1f3e23d12a321: ooo\|F(-x)(-x)\|Ffo\|oFo\|of(-x) 3 oof\|(-x)oF\|ooo\|Fo(-x)\|foo 3 (-x)fo\|oFo\|ofF\|(-x)(-x)F\|ooo &#xt → †)
Stott expansion: (derived potential CRFs)	1:A1F1d1: oxxFxoAFxxFoxFx 3 xofoxFooofxxfoo 3 ofoxfoofFxofoox &#xt ...	1:A1E21F1d1: oxxFooAFxxFoxFx 3 xofooFooofxxfoo 3 ofoxFoofFxofoox &#xt ...
	2:E2e2: xoofxxFfooFxofo 3 xxFxoFxxxFoxFxx 3 ofoxFoofFxxfoox &#xt → CRF with cell list: 24 ikes 16 octs 72 squippies (J1) 198 tets 24 tricues (J3) 48 trips 2 tuts related: xo.fxxFfooFx.fo 3 xx.xoFxxxFox.xx 3 of.xFoofFxxf.ox &#xt → CRF with cell list: 24 gyepips (J11) 12 mibdies (J62) 16 octs 72 squippies (J1) 78 tets 24 tricues (J3) 48 trips 2 tuts	2:A12E2\|e2: ooofxx\|Ffo\|oFxofo 3 oxFxoF\|xxx\|FoxFxx 3 xfoxFo\|ofF\|xxfoox &#xt → CRF with cell list: 24 ikes 16 octs 72 squippies (J1) 155 tets 4 thawroes (J92) 16 tricues (J3) 36 trips 1 tut (asymmetric hemiglomal combination of others)
	2:D32E2\|e2: xooFxx\|Ffo\|oFxofo 3 xxFooF\|xxx\|FoxFxx 3 ofooFo\|ofF\|xxfoox &#xt → CRF with cell list: 12 bilbiroes (J91) 12 ikes 12 mibdies (J62) 16 octs 48 squippies (J1) 122 tets 16 tricues (J3) 24 trips 2 tuts (asymmetric hemiglomal combination of others)	2:A12E2\|e2d12: ooofxx\|Ffo\|oFoofo 3 oxFxoF\|xxx\|FooFxx 3 xfoxFo\|ofF\|xxFoox &#xt → CRF with cell list: 12 bilbiroes (J91) 12 ikes 12 mibdies (J62) 16 octs 48 squippies (J1) 79 tets 4 thawroes (J92) 8 tricues (J3) 12 trips 1 tut (asymmetric hemiglomal combination of others)
	2:A12E2e2a32: ooofxxFfooFxofx 3 oxFxoFxxxFoxFxo 3 xfoxFoofFxxfooo &#xt → CRF with cell list: 24 ikes 16 octs 72 squippies (J1) 112 tets 8 thawroes (J92) 8 tricues (J3) 24 trips	2:D32E2e2d12: xooFxxFfooFoofo 3 xxFooFxxxFooFxx 3 ofooFoofFxxFoox &#xt → CRF with cell list: 24 bilbiroes (J91) 24 mibdies (J62) 16 octs 24 squippies (J1) 46 tets 8 tricues (J3) 2 tuts
	12:A12E21F1e2d12: xxxFooAFxxAxxFx 3 oxFxxAxxxFooFxx 3 xfoxFoofFxxFoox &#xt → CRF with cell list: 24 bilbiroes (J91) 1 co 8 octs 30 pips 18 squippies (J1) 24 teddies (J63) 12 tets 4 thawroes (J92) 1 toe 28 tricues (J3) 24 trips	13:A1D3F1f3d1a3: oxxFxoAFxxFoxFx 3 xofxxFoooFxxfox 3 xFxoFxxFAoxFxxo &#xt → CRF with cell list: 24 bilbiroes (J91) 16 octs 48 squippies (J1) 24 teddies (J63) 30 tets 8 thawroes (J92) 16 tricues (J3) 48 trips 2 tuts
	13:A1D3E21F1f3d1a3: oxxFooAFxxFoxFx 3 xofxoFoooFxxfox 3 xFxoAxxFAoxFxxo &#xt ...	13:A1D3E21F1f3e23d1a3: oxxFooAFxxAoxFx 3 xofxoFoooFoxfox 3 xFxoAxxFAooFxxo &#xt ...
using here node marks / (pseudo) edge lengths: `F=f+x, A=F+x=f+2x`

in `o2o2o2o` subsymmetry (up)
Representation:	ooo\|xxx\|fff\|FFF\|Vooo\|f 2 Fxf\|oFf\|xFo\|fxo\|oVoo\|f 2 xfF\|Ffo\|Fox\|xof\|ooVo\|f 2 fFx\|foF\|oxF\|ofx\|oooV\|f &#zx (ex)
All layers & kaleido-facetings per layer:	A: o2F2x2f → A3: o 2 F 2(-x)2 f B: o2x2f2F → B2: o 2(-x)2 f 2 F C: o2f2F2x → C4: o 2 f 2 F 2(-x) D: x2o2F2f → D1: (-x)2 o 2 F 2 f E: x2F2f2o → E1: (-x)2 F 2 f 2 o F: x2f2o2F → F1: (-x)2 f 2 o 2 F G: f2x2F2o → G2: f 2(-x)2 F 2 o H: f2F2o2x → H4: f 2 F 2 o 2(-x) I: f2o2x2F → I3: f 2 o 2(-x)2 F	J: F2f2x2o → J3: F 2 f 2(-x)2 o K: F2x2o2f → K2: F 2(-x)2 o 2 f L: F2o2f2x → L4: F 2 o 2 f 2(-x) M: V2o2o2o N: o2V2o2o O: o2o2V2o P: o2o2o2V Q: f2f2f2f
A priori invalid combinations:	A + I3,J3 A3 + I,J B + G2,K2 B2 + G,K C + H4,L4 C4 + H,L D + E1,F1 D1 + E,F	E + F1 E1 + F G + K2 G2 + K H + L4 H4 + L I + J3 I3 + J (all giving rise to u edges)
Other layer-combinations:	ABCD1E1F1GHIJKL: ooo(-x)(-x)(-x)fffFFFVooof 2 FxfoFfxFofxooVoof 2 xfFFfoFoxxofooVof 2 fFxfoFoxFofxoooVf &#zx ABC4D1E1F1GH4IJKL4: ooo(-x)(-x)(-x)fffFFFVooof 2 FxfoFfxFofxooVoof 2 xfFFfoFoxxofooVof 2 fF(-x)foFo(-x)Fof(-x)oooVf &#zx AB2C4D1E1F1G2H4IJK2L4: ooo(-x)(-x)(-x)fffFFFVooof 2 F(-x)foFf(-x)Fof(-x)ooVoof 2 xfFFfoFoxxofooVof 2 fF(-x)foFo(-x)Fof(-x)oooVf &#zx A3B2C4D1E1F1G2H4I3J3K2L4: ooo(-x)(-x)(-x)fffFFFVooof 2 F(-x)foFf(-x)Fof(-x)ooVoof 2 (-x)fFFfoFo(-x)(-x)ofooVof 2 fF(-x)foFo(-x)Fof(-x)oooVf &#zx → †)
Stott expansion: (derived potential CRFs)	1:ABCD1E1F1GHIJKL: xxxoooFFFAAABxxxF 2 FxfoFfxFofxooVoof 2 xfFFfoFoxxofooVof 2 fFxfoFoxFofxoooVf &#zx (telex) → CRF with cell list: 24 ikes 60 squippies (J1) 180 tets 20 trips (as this is just an axial change, the orthogonal symmetry remains; thus it also can be described as: BAFox 2 oxofo 3 oooox 5 ooxoo &#zx) related: xxxoooFFF.......F 2 FxfoFfxFo.......f 2 xfFFfoFox.......f 2 fFxfoFoxF.......f &#zx → CRF with cell list: 6 bilbiroes (J91) 2 does 24 mibdies (J62) 36 squippies (J1) 16 tets 8 trips
	14:ABC4D1E1F1GH4IJKL4: xxxoooFFFAAABxxxF 2 FxfoFfxFofxooVoof 2 xfFFfoFoxxofooVof 2 FAoFxAxoAxFoxxxBF &#zx → CRF with cell list: 16 bilbiroes (J91) 16 gyepips (J11) 64 squippies (J1) 16 teddies (J63) 24 tets 24 trips related: xxxoooFFFAAA.xx.F FxfoFfxFofxo.Vo.f xfFFfoFoxxof.oV.f FAoFxAxoAxFo.xx.F&#zx → CRF with cell list: 20 bilbiroes (J91) 16 paps 48 squippies (J1) 16 teddies (J63) 8 tets 16 trips
	124:AB2C4D1E1F1G2H4IJK2L4: xxxoooFFFAAABxxxF 2 AoFxAFoAxFoxxBxxF 2 xfFFfoFoxxofooVof 2 FAoFxAxoAxFoxxxBF &#zx → °)
using here node marks / (pseudo) edge lengths: `F=f+x=ff, V=2f, A=F+x=f+2x, B=V+x=2f+x=fff`

EKF of the icositetrachoron (`x3o4o3o`)

©

in `o3o3o4o` subsymmetry (up)
Representation:	qo 3 oo 3 oo 4 ox &#zx (ico)
All layers & kaleido-facetings per layer:	A: q3o3o4o B: o3o3o4x → B4: o3o3q4(-x)
A priori invalid combinations:	none
Other layer-combinations:	B4: qo 3 oo 3 oq 4 o(-x) &#zx
Stott expansion: (derived potential CRFs)	1:-: wx 3 oo 3 oo 4 ox &#zx (poxic) → CRF with cell list: 24 esquidpies (J15) 16 tets 32 trips	2:-: qo 3 xx 3 oo 4 ox &#zx = Wythoffian `x3o4o3x` (spic) with cell list: 48 octs 192 trips
	3:-: qo 3 oo 3 xx 4 ox &#zx (pocsric) → CRF with cell list: 8 coes 24 squobcues (J28) 16 tets 64 trips	4:B4: qo 3 oo 3 oq 4 xo &#zx = Wythoffian `o3x4o3o` (rico) with cell list: 24 coes 24 cubes
	12:-: wx 3 xx 3 oo 4 ox &#zx (owauprit) → CRF with cell list: 24 esquidpies (J15) 32 hips 8 octs 160 trips 16 tuts	13:-: wx 3 oo 3 xx 4 ox &#zx = Wythoffian `x3o4x3o` (srico) with cell list: 24 coes 24 sircoes 96 trips
	14:B4: wx 3 oo 3 oq 4 xo &#zx → °) (asks for non-regular hexagons: wx .. oq .. &#zx)	23:-: qo 3 xx 3 xx 4 ox &#zx (pocprico) → CRF with cell list: 64 hips 24 squobcues (J28) 8 toes 128 trips 16 tuts
	24:B4: qo 3 xx 3 oq 4 xo &#zx = Wythoffian `x3o4x3o` (srico) with cell list: 24 coes 24 sircoes 96 trips	34:B4: qo 3 oo 3 xw 4 xo &#zx → °) (asks for non-regular hexagons: qo .. xw .. &#zx)
	123:-: wx 3 xx 3 xx 4 ox &#zx = Wythoffian `x3x4o3x` (prico) with cell list: 96 hips 24 sircoes 24 toes 96 trips	124:B4: wx 3 xx 3 oq 4 xo &#zx → °) (asks for non-regular hexagons: wx .. oq .. &#zx)
	134:B4: wx 3 oo 3 xw 4 xo &#zx = Wythoffian `o3x4x3o` (cont) with cell list: 48 tics	234:B4: qo 3 xx 3 xw 4 xo &#zx → °) (asks for non-regular hexagons: qo .. xw .. &#zx)
	1234:B4: wx 3 xx 3 xw 4 xo &#zx = Wythoffian `x3x4x3o` (grico) with cell list: 24 gircoes 24 tics 96 trips

(As it will turn out, the set of resulting polychora in o2o3o4o resp. . o3o4o here is identical to those which turn up from the corresponding consideration of hex wrt. these subsymmetries.)

in `o2o3o4o` subsymmetry (up)
Representation:	qo 2 xo 3 ox 4 oo &#zx (ico)
All layers & kaleido-facetings per layer:	A: q2x3o4o → A2: q 2(-x)3 x 4 o → A23: q 2 o 3(-x)4 q B: o2o3x4o → B3: o 2 x 3(-x)4 q → B32: o 2(-x)3 o 4 q
A priori invalid combinations:	A23 → ‡) (q or w in extremal layers, i.e. A) B32 + neither A2 nor A23 → ‡) (u in A) A2 + B3 → ‡) (u in A, u in B)
Other layer-combinations:	A2: qo 2 (-x)o 3 xx 4 oo &#zx A2B32: qo 2 (-x)(-x) 3 xo 4 oq &#zx B3: qo 2 xx 3 o(-x) 4 oq &#zx
Stott expansion: (derived potential CRFs)	1:-: wx 2 xo 3 ox 4 oo &#zx (pexic) → CRF with cell list: 6 esquidpies (J15) 18 octs 8 trips	2:A2: qo 2 ox 3 xx 4 oo &#zx (coatobcu) → CRF with cell list: 2 coes 12 cubes 16 tricues (J3)
	2:A2B32: qo 2 oo 3 xo 4 oq &#zx = Wythoffian `o3o3x4o` (rit) with cell list: 8 coes 16 tets	3:B3: qo 2 xx 3 xo 4 oq &#zx (pabdirico) → CRF with cell list: 6 coes 12 cubes 2 toes 16 tricues (J3)
	4:-: qo 2 xo 3 ox 4 xx &#zx (pacsrit) → CRF with cell list: 16 octs 2 sircoes 6 squobcues (J28) 24 trips	12:A2: wx 2 ox 3 xx 4 oo &#zx → CRF with cell list: 2 coes 18 cubes 8 hips 16 tricues (J3)
	12:A2B32: wx 2 oo 3 xo 4 oq &#zx → °) (asks for non-regular hexagons: wx .. .. oq &#zx)	13:B3: wx 2 xx 3 xo 4 oq &#zx → °) (asks for non-regular hexagons: wx .. .. oq &#zx)
	14:-: wx 2 xo 3 ox 4 xx &:#zx = Wythoffian `o3x3o4x` (srit) with cell list: 16 octs 8 sircoes 32 trips	2(-3):A2: qo 2 ox 3 oo 4 oo &#zx = Wythoffian `x3o3o4o` (hex) with cell list: 16 tets
	24:A2: qo 2 ox 3 xx 4 xx &#zx (tica gircobcu) → CRF with cell list: 12 ops 2 tics 16 tricues (J3) 24 trips	24:A2B32: qo 2 oo 3 xo 4 xw &#zx → °) (asks for non-regular hexagons: qo .. .. xw &#zx)
	34:B3: qo 2 xx 3 xo 4 xw &#zx → °) (asks for non-regular hexagons: qo .. .. xw &#zx)	12(-3):A2: wx 2 ox 3 oo 4 oo &#zx (pex hex) → CRF with cell list: 16 tets 8 trips
	124:A2: wx 2 ox 3 xx 4 xx &#zx → CRF with cell list: 12 cubes 8 hips 18 ops 2 tics 16 tricues (J3) 24 trips	124: A2B32: wx 2 oo 3 xo 4 xw &#zx = Wythoffian `o3o3x4x` (tat) with cell list: 16 tets 8 tics
	134:B3: wx 2 xx 3 xo 4 xw &#zx (pabdiproh) → CRF with cell list: 2 gircoes 12 ops 6 tics 16 tricues (J3) 8 trips	2(-3)4:A2: qo 2 ox 3 oo 4 xx &#zx (pacsid pith) → CRF with cell list: 14 cubes 16 tets 24 trips
	12(-3)4:A2: wx 2 ox 3 oo 4 xx &#zx = Wythoffian `x3o3o4x` (sidpith) with cell list: 32 cubes 16 tets 32 trips
in `. o3o4o` subsymmetry (up)
additional, not prismatically symmetric combinations of formers:	none (As A23 already was ruled out a priori this would ask for a local A and A2 at the top resp. bottom layer. But that combination would suffer again from producing an u=2x sized edge in A.)

in `o3o3o *b3o` subsymmetry (up)
Representation:	qoo 3 ooo 3 oqo *b3 ooq &#zx (ico)
All layers & kaleido-facetings per layer:	A: q3o3o b3o B: o3o3q b3o C: o3o3o *b3q (As this representation does not show up (true / x-) edges within the layers, those thus cannot be inverted either. Therefore at most pure partial Stott expansions wrt. this subsymmetry remain possible.)
Stott expansion: (derived potential CRFs)	1:-: wxx 3 ooo 3 oqo b3 ooq &#zx (poxic) → CRF with cell list: 24 esquidpies (J15) 16 tets 32 trips related: .xx 3 .oo 3 .qo b3 .oq &#zx = Wythoffian x3o3o4x (sidpith) with cell list: 32 cubes 16 tets 32 trips	2:-: qoo 3 xxx 3 oqo b3 ooq &#zx = Wythoffian `x3o4o3x` (spic) with cell list: 48 octs 192 trips related: .oo 3 .xx 3 .qo b3 .oq &#zx = Wythoffian o3x3o4x (srit) with cell list: 16 octs 8 sircoes 32 trips
	12:-: wxx 3 xxx 3 oqo b3 ooq &#zx (owau prit) → CRF with cell list: 24 esquidpies (J15) 32 hips 8 octs 160 trips 16 tuts related: .xx 3 .xx 3 .qo b3 .oq &#zx = Wythoffian x3x3o4x (prit) with cell list: 24 cubes 32 hips 8 sircoes 16 tuts	13:-: wxx 3 ooo 3 xwx b3 ooq &#zx (pocsric) → CRF with cell list: 8 coes 24 squobcues (J28) 16 tets 64 trips related: wx. 3 oo. 3 xw. b3 oo. &#zx = Wythoffian x3o3x4x (tat) with cell list: 16 tets 8 tics
	123:-: wxx 3 xxx 3 xwx b3 ooq &#zx (poc prico) → CRF with cell list: 64 hips 24 squobcues (J28) 8 toes 128 trips 16 tuts related: wx. 3 xx. 3 xw. b3 oo. &#zx = Wythoffian o3x3x4x (grit) with cell list: 8 gircoes 32 trips 16 tuts	134:-: wxx 3 ooo 3 xwx b3 xxw &#zx = Wythoffian `x3o4x3o` (srico) with cell list: 24 coes 24 sircoes 96 trips related: wx. 3 oo. 3 xw. b3 xx. &#zx = Wythoffian x3o3x4x (proh) with cell list: 16 coes 24 ops 8 tics 32 trips
	1234:-: wxx 3 xxx 3 xwx b3 xxw &#zx = Wythoffian `x3x4o3x` (prico) with cell list: 96 hips 24 sircoes 24 toes 96 trips related: .xx 3 .xx 3 .wx b3 .xw &#zx = Wythoffian x3x3x4x (gidpith) with cell list: 8 gircoes 32 hips 24 ops 16 toes

in `o4o2o4o` subsymmetry (up)
Representation:	oxo 4 ooq 2 oxo 4 qoo &#zx (ico)
All layers & kaleido-facetings per layer:	A: o4o o4q B: x4o x4o → B1: (-x)4q x4o → B13: (-x)4q (-x)4q ↳ B3: x4o (-x)4q → (B31 = B13) C: o4q o4o
Stott expansion: (derived potential CRFs)	1:B1: xox 4 oqq 2 oxo 4 qoo &#zx → ‡) (q in C)	2:-: oxo 4 xxw 2 oxo 4 qoo &#zx (bicyte ausodip) → CRF with cell list: 4 esquidpies (J15) 16 octs 4 squobcues (J28) 16 trips related: .xo 4 .xw 2 .xo 4 .oo &#zx (cyte cubau sodip) → CRF with cell list: 4 esquidpies (J15) 4 ops 16 squippies (J1)
	12:B1: xox 4 xww 2 oxo 4 qoo &#zx → ‡) (w in C)	13:B13: xox 4 oqq 2 xox 4 qqo &#zx → ‡) (q in A, q in C)
	24:-: oxo 4 xxw 2 oxo 4 wxx &#zx = Wythoffian `o3x3o4x` (srit) with cell list: 16 octs 8 sircoes 32 trips related: .xo 4 .xw 2 .xo 4 .xx &#zx (cyted srit) → CRF with cell list: 8 ops 4 sircoes 16 squippies (J1) 16 trips	123:B13: xox 4 xww 2 xox 4 qqo &#zx → ‡) (q in A, w in C)
	124:B1: xox 4 xww 2 oxo 4 wxx &#zx → ‡) (w in C)	1234:B13: xox 4 xww 2 xox 4 wwx &#zx → ‡) (w in A, w in C)

EKF of the hexadecachoron (`x3o3o4o`)

©

(As it will turn out, the set of resulting polychora in o2o3o4o resp. . o3o4o here is identical to those which turn up from the corresponding consideration of ico wrt. these subsymmetries.)

in `o2o3o4o` subsymmetry (up)
Representation:	qo 2 ox 3 oo 4 oo &#zx (hex)
All layers & kaleido-facetings per layer:	A: q2o3o4o B: o2x3o4o → B2: o 2(-x)3 x 4 o → B23: o 2 o 3(-x)4 q
A priori invalid combinations:	none
Stott expansion: (derived potential CRFs)	1:-: wx 2 ox 3 oo 4 oo &#zx (pex hex) = oxxo 3 oooo 4 oooo &#xt → CRF with cell list: 16 tets 8 trips	2:B2: qo 2 xo 3 ox 4 oo &#zx = xox 3 oxo 4 ooo &#xt = Wythoffian `x3o4o3o` (ico) with cell list: 24 octs
	3:-: qo 2 ox 3 xx 4 oo &#zx (coatobcu) = oxo 3 xxx 4 ooo &#xt → CRF with cell list: 2 coes 12 cubes 16 tricues (J3)	3:B23: qo 2 oo 3 xo 4 oq &#zx = ooo 3 xox 4 oqo &#xt = Wythoffian `o3o3x4o` (rit) with cell list: 8 coes 16 tets
	4:-: qo 2 ox 3 oo 4 xx &#zx (pacsid pith) = oxo 3 ooo 4 xxx &#xt → CRF with cell list: 14 cubes 16 tets 24 trips	12:B2: wx 2 xo 3 ox 4 oo &#zx (pexic) = xoox 3 oxxo 4 oooo &#xt → CRF with cell list: 6 esquidpies (J15) 18 octs 8 trips
	13:-: wx 2 ox 3 xx 4 oo &#zx = oxxo 3 xxxx 4 oooo &#xt → CRF with cell list: 2 coes 18 cubes 8 hips 16 tricues (J3)	13:B23: wx 2 oo 3 xo 4 oq &#zx → °) (asks for non-regular hexagons: wx .. .. oq &#zx)
	14:-: wx 2 ox 3 oo 4 xx &#zx = oxxo 3 oooo 4 xxxx &#xt = Wythoffian `x3o3o4x` (sidpith) with cell list: 32 cubes 16 tets 32 trips	23:B23: qo 2 xx 3 xo 4 oq &#zx (pabdirico) = xxx 3 xox 4 oqo &#xt → CRF with cell list: 6 coes 12 cubes 2 toes 16 tricues (J3)
	24:B2: qo 2 xo 3 ox 4 xx &#zx (pacsrit) = xox 3 oxo 4 xxx &#xt → CRF with cell list: 16 octs 2 sircoes 6 squobcues (J28) 24 trips	34:-: qo 2 ox 3 xx 4 xx &#zx (tica gircobcu) = oxo 3 xxx 4 xxx &#xt → CRF with cell list: 12 ops 2 tics 16 tricues (J3) 24 trips
	34:B23: qo 2 oo 3 xo 4 xw &#zx → °) (asks for non-regular hexagons: qo .. .. xw &#zx)	123:B23: wx 2 xx 3 xo 4 oq &#zx → °) (asks for non-regular hexagons: wx .. .. oq &#zx)
	124:B2: wx 2 xo 3 ox 4 xx &#zx = xoox 3 oxxo 4 xxxx &#xt = Wythoffian o3x3o4x (srit) with cell list: 16 octs 8 sircoes 32 trips	134:-: wx 2 ox 3 xx 4 xx &#zx = oxxo 3 xxxx 4 xxxx &#xt → CRF with cell list: 12 cubes 8 hips 18 ops 2 tics 16 tricues (J3) 24 trips
	134:B23: wx 2 oo 3 xo 4 xw &#zx = oooo 3 xoox 4 xwwx &#xt = Wythoffian o3o3x4x (tat) with cell list: 16 tets 8 tics	234:B23: qo 2 xx 3 xo 4 xw &#zx → °) (asks for non-regular hexagons: qo .. .. xw &#zx)
	1234:B23: wx 2 xx 3 xo 4 xw &#zx (pabdiproh) = xxxx 3 xoox 4 xwwx &#xt → CRF with cell list: 2 gircoes 12 ops 6 tics 16 tricues (J3) 8 trips
in `. o3o4o` subsymmetry (up)
additional, not prismatically symmetric combinations of formers:	none

in `. o3o3o` subsymmetry (up)
Representation:	xo 3 oo 3 ox &#x (hex)
All layers & kaleido-facetings per layer:	A: x3o3o → A1:(-x)3 x 3 o → A12: o 3(-x)3 x → A123: o 3 o 3(-x) B: o3o3x → B3: o 3 x 3(-x) → B32: x 3(-x)3 o → B321:(-x)3 o 3 o
A priori invalid combinations:	A + B321 → ‡) (u in A) A1 + B32 → ‡) (u in A, u in B) A12 + B3 → ‡) (u in A, u in B) A123 + B → ‡) (u in B)
Stott expansion: (derived potential CRFs)	1:A1: ox 3 xo 3 ox &#x (octaco) → CRF (segmentochoron) with cell list: 1 co 9 octs 6 squippies (J1)	1:A1B321: oo 3 xo 3 oo &#x (octpy) → CRF (segmentochoron) with cell list: 1 oct 8 tets
	2:-: xo 3 xx 3 ox &#x (tuta) → CRF (segmentochoron) with cell list: 6 tets 8 tricues (J3) 2 tuts	2:A12: oo 3 ox 3 xx &#x (tetatut) → CRF (segmentochoron) with cell list: 5 tets 4 tricues (J3) 1 tut
	2:A12B32: ox 3 oo 3 xo &#x = Wythoffian x3o3o4o (hex) with cell list: 16 tets (axially dual orientation)	12:A12: xx 3 ox 3 xx &#x (coatoe) → CRF (segmentochoron) with cell list: 1 co 6 cubes 1 toe 8 tricues (J3)
	12:A12B321: xo 3 ox 3 xo &#x (octaco) → CRF (segmentochoron) with cell list: 1 co 9 octs 6 squippies (J1)	13:A1B3: ox 3 xx 3 xo &#x (tuta) → CRF (segmentochoron) with cell list: 6 tets 8 tricues (J3) 2 tuts
	13:A1B321: oo 3 xo 3 xx &#x (tetatut) → CRF (segmentochoron) with cell list: 5 tets 4 tricues (J3) 1 tut	13:A123B321: xo 3 oo 3 ox &#x = Wythoffian x3o3o4o (hex) with cell list: 16 tets (identical orientation)
	123:A123B321: xo 3 xx 3 ox &#x (tuta) → CRF (segmentochoron) with cell list: 6 tets 8 tricues (J3) 2 tuts

in `o4o2o4o` subsymmetry (up)
Representation:	xo 4 oo 2 ox 4 oo &#zx (hex)
All layers & kaleido-facetings per layer:	A: x4o o4o → A1: (-x)4 q o 4 o B: o4o x4o → B3: o 4 o (-x)4 q
Stott expansion: (derived potential CRFs)	1:A1: ox 4 qo 2 ox 4 oo &#zx (cytau tes) → CRF with cell list: 4 cubes 4 octs 16 squippies (J1)	2:-: xo 4 xx 2 ox 4 oo &#zx (quawros) → CRF with cell list: 4 cubes 16 tets 16 trips
	12:A1: ox 4 wx 2 ox 4 oo &#zx (cyte cubau sodip) → CRF with cell list: 4 esquidpies (J15) 4 ops 16 squippies (J1)	13:A1B3: ox 4 qo 2 xo 4 oq &#zx = Wythoffian o3o3x4o (rit) with cell list: 8 coes 16 tets
	14:A1: ox 4 qo 2 ox 4 xx &#zx (cyte opau sodip) → CRF with cell list: 8 cubes 16 squippies (J1) 4 squobcues (J28) 16 trips	24:-: xo 4 xx 2 ox 4 xx &#zx = Wythoffian x3o3o4x (sidpith) with cell list: 32 cubes 16 tets 32 trips
	123:A1B3: ox 4 wx 2 xo 4 oq &#zx → °) (asks for non-regular hexagons: .. wx .. oq &#zx)	124:A1: ox 4 wx 2 ox 4 xx &#zx (cyted srit) → CRF with cell list: 8 ops 4 sircoes 16 squippies (J1) 16 trips
	1234:A1B3: ox 4 wx 2 xo 4 xw &#zxx = Wythoffian o3o3x4x (tat) with cell list: 16 tets 8 tics

in `o2o2o2o` subsymmetry (up)
Representation:	qooo 2 oqoo 2 ooqo 2 oooq &#zx (hex)
All layers & kaleido-facetings per layer:	A: q2o2o2o B: o2q2o2o C: o2o2q2o D: o2o2o2q (As this representation does not show up (true / x-) edges within the layers, those thus cannot be inverted either. Therefore at most pure partial Stott expansions wrt. this subsymmetry remain possible.)
Stott expansion: (derived potential CRFs)	1:A1: wxxx 2 oqoo 2 ooqo 2 oooq &#zx (pexhex) → CRF with cell list: 16 tets 8 trips related: .xxx 2 .qoo 2 .oqo 2 .ooq &#zx = Wythoffian x x3o4o (ope) with cell list: 2 octs 8 trips	12:-: wxxx 2 xwxx 2 ooqo 2 oooq &#zx (quawros) → CRF with cell list: 4 cubes 16 tets 16 trips
	123:-: wxxx 2 xwxx 2 xxwx 2 oooq &#zx (pacsid pith) → CRF with cell list: 14 cubes 16 tets 24 trips	1234:-: wxxx 2 xwxx 2 xxwx 2 xxxw &#zx = Wythoffian x3o3o4x (sidpith) with cell list: 32 cubes 16 tets 32 trips related: .xxx 2 .wxx 2 .xwx 2 .xxw &#zx = Wythoffian x x3o4x (sircope) with cell list: 18 cubes 2 sircoes 8 trips

EKF of the pentachoron (`x3o3o3o`)

©

(As it will turn out, the set of resulting polychora in . o3o3o here is identical to those which turn up from the corresponding consideration of rap wrt. this subsymmetry.)

in `. o3o3o` subsymmetry (up)
Representation:	ox 3 oo 3 oo &#x (pen)
All layers & kaleido-facetings per layer:	A: o3o3o B: x3o3o → B1:(-x)3 x 3 o → B12: o 3(-x)3 x → B123: o 3 o 3(-x)
A priori invalid combinations:	none
Stott expansion: (derived potential CRFs)	1:B1: xo 3 ox 3 oo &#x = Wythoffian `o3x3o4o` (rap) with cell list: 5 octs 5 tets	2:-: ox 3 xx 3 oo &#x (octatut) → CRF (segmentochoron) with cell list: 1 oct 4 tricues (J3) 4 trips 1 tut
	2:B12: oo 3 xo 3 ox &#x = Wythoffian `o3x3o3o` (rap) with cell list: 5 octs 5 tets (inverted orientation)	3:-: ox 3 oo 3 xx &#x (tetaco) → CRF (segmentochoron) with cell list: 1 co 5 tets 10 trips
	3:B123: oo 3 oo 3 xo &#x = Wythoffian `o3o3o3x` (pen) with cell list: 5 tets (dual orientation)	12:B12: xx 3 xo 3 ox &#x (coatut) → CRF (segmentochoron) with cell list: 1 co 4 octs 4 tricues (J3) 6 trips 1 tut
	13:B1: xo 3 ox 3 xx &#x (coatut) → CRF (segmentochoron) with cell list: 1 co 4 octs 4 tricues (J3) 6 trips 1 tut (inverted orientation)	13:B123: xx 3 oo 3 xo &#x (tetaco) → CRF (segmentochoron) with cell list: 1 co 5 tets 10 trips (inverted orientation)
	23:-: ox 3 xx 3 xx &#x (tutatoe) → CRF (segmentochoron) with cell list: 4 hips 1 toe 4 tricues (J3) 6 trips 1 tut	23:B123: oo 3 xx 3 xo &#x (octatut) → CRF (segmentochoron) with cell list: 1 oct 4 tricues (J3) 4 trips 1 tut
	123:B123: xx 3 xx 3 xo &#x (tutatoe) → CRF (segmentochoron) with cell list: 4 hips 1 toe 4 tricues (J3) 6 trips 1 tut (inverted orientation)

EKF of the rectified pentachoron (`o3x3o3o`)

(As it will turn out, the set of resulting polychora in . o3o3o here is identical to those which turn up from the corresponding consideration of pen wrt. this subsymmetry.)

in `. o3o3o` subsymmetry (up)
Representation:	xo 3 ox 3 oo &#x (rap)
All layers & kaleido-facetings per layer:	A: x3o3o → A1: (-x)3x3o → A12: o3(-x)3x → A123: o3o3(-x) B: o3x3o → B2: x3(-x)3x → B21: (-x)3o3x → B213: (-x)3x(-x) → B2132: o3(-x)3o ↳ B23: x3o3(-x) → B231 = B213
A priori invalid combinations:	A + B21,B213 A1 + B2,B2132,B23 A12 + B,B213,B23 A123 + B2,B21
Other layer-combinations:	B2: xx3o(-x)3ox&#x B2132: xo3o(-x)3oo&#x → ‡ B23: xx3oo3o(-x)&#x A1: (-x)o3xx3oo&#x A1B21: (-x)(-x)3xo3ox&#x A1B213: (-x)(-x)3xx3o(-x)&#x A12B2: ox3(-x)(-x)3xx&#x A12B2132: oo3(-x)(-x)3xo&#x A123: oo3ox3(-x)o&#x → ‡ A123B213: o(-x)3ox3(-x)(-x)&#x A123B2132: oo3o(-x)3(-x)o&#x A123B23: ox3oo3(-x)(-x)&#x
Stott expansion: (derived potential CRFs)	1:A1 = 23:A123B23: ox 3 xx 3 oo &#x (octatut) → CRF (segmentochoron) with cell list: 1 oct 4 tricues (J3) 4 trips 1 tut	1:A1B21 = 23:A123B2132: oo 3 xo 3 ox &#x = Wythoffian `o3x3o3o` (rap) with cell list: 5 octs 5 tets (inverted orientation)
	2:B2 = 123:A123B2132: xx 3 xo 3 ox &#x (coatut) → CRF (segmentochoron) with cell list: 1 co 4 octs 4 tricues (J3) 6 trips 1 tut	2:A12B2: ox 3 oo 3 xx &#x (tetaco) → CRF (segmentochoron) with cell list: 1 co 4 octs 4 tricues (J3) 6 trips 1 tut
	2:A12B2132: oo 3 oo 3 xo &#x = Wythoffian `x3o3o3o` (pen) with cell list: 5 tets	3:-: xo 3 ox 3 xx &#x (coatut) → CRF (segmentochoron) with cell list: 1 co 4 octs 4 tricues (J3) 6 trips 1 tut (inverted orientation)
	3:A123B23: ox 3 oo 3 oo &#x = Wythoffian `o3o3o3x` (pen) with cell list: 5 tets (dual orientation)	12:A12B2132: xx 3 oo 3 xo &#x (tetaco) → CRF (segmentochoron) with cell list: 1 co 4 octs 4 tricues (J3) 6 trips 1 tut (inverted orientation)
	13:A1: ox 3 xx 3 xx &#x (tutatoe) → CRF (segmentochoron) with cell list: 4 hips 1 toe 4 tricues (J3) 6 trips 1 tut	13:A1B213: oo 3 xx 3 xo &#x (octatut) → CRF (segmentochoron) with cell list: 1 oct 4 tricues (J3) 4 trips 1 tut (inverted orientation)
	13:A123B213: xo 3 ox 3 oo &#x = Wythoffian `o3x3o3o` (rap) with cell list: 5 octs 5 tets (itself again)	23:B23: xx 3 xx 3 xo &#x (tutatoe) → CRF (segmentochoron) with cell list: 4 hips 1 toe 4 tricues (J3) 6 trips 1 tut (inverted orientation)

EKF of the small rhombated pentachoron (`x3o3x3o`)

(As it will turn out, the set of resulting polychora in . o3o3o here is identical to those which turn up from the corresponding consideration of spid wrt. this subsymmetry.)

in `. o3o3o` subsymmetry (up)
Representation:	oxx 3 xxo 3 oox &#xt (srip)
All layers & kaleido-facetings per layer:	A: o3x3o → A2: x 3(-x)3 x → A21: (-x)3 o 3 x → A213: (-x)3 x 3(-x) → A2132: o 3(-x)3 o ↳ A23: x 3 o 3(-x) → (A231 = A213) → (A2312 = A2132) B: x3x3o → B1:(-x)3 u 3 o ↳ B2: u 3(-x)3 x → B23: u 3 o 3(-x) C: x3o3x → C1:(-x)3 x 3 x → C12: o 3(-x)3 u ↳ C13: (-x)3 u 3(-x) ↳ C3: x 3 x 3(-x) → (C31 = C13) ↳ C32: u 3(-x)3 o
A priori invalid combinations:	A + B2,B23 A + C12,C32 A2 + B,B1,B23 A2 + C1,C3,C13 A21 + B,B1,B2,B23 → generally A23 + B1,B2 A23 + C,C1,C12 A213 + B,B2,B23 A213 + C,C1,C3,C12,C32 A2132 + B,B1,B2,B23 → generally B + C1,C12,C13,C32 B1 + C,C3,C12,C32 B2 + C1,C3,C12,C32 B23 + C,C1,C12,C13 C12 generally (u in extremal layer) C13 generally (u in extremal layer) C32 generally (u in extremal layer)
Other layer-combinations:	B1C1: o(-x)(-x) 3 xux 3 oox &#xt A2B2: xux 3 (-x)(-x)o 3 xxx &#xt C3: oxx 3 xxx 3 oo(-x) &#xt A23C3: xxx 3 oxx 3 (-x)o(-x) &#xt → †) A23B23C3: xux 3 oox 3 (-x)(-x)(-x) &#xt
Stott expansion: (derived potential CRFs)	1:B1C1: xoo 3 xux 3 oox &#xt = Wythoffian `o3x3x3o` (deca) with cell list: 10 tuts	2:A2B2: xux 3 oox 3 xxx &#xt (coatotum) → CRF with cell list: 1 co 6 hips 1 toe 4 tricues (J3) 4 trips 4 tuts
Stott expansion: (derived potential CRFs)	3:C3: oxx 3 xxx 3 xxo &#xt (tutatoe gybcu) → CRF with cell list: 8 hips 8 tricues (J3) 12 trips 2 tuts (bistratic segmentochoral stack) related: ox. 3 xx. 3 xx. &#x (tutatoe) → CRF (segmentochoron) with cell list: 4 hips 1 toe 4 tricues (J3) 6 trips 1 tut	3:A23B23C3: xux 3 oox 3 ooo &#xt = Wythoffian `x3x3o3o` (tip) with cell list: 5 tets 5 tuts

EKF of the decachoron (`o3x3x3o`)

©

in `. o3o3o` subsymmetry (up)
Representation:	oox 3 xux 3 xoo &#xt (deca)
All layers & kaleido-facetings per layer:	A: o3x3x → A2: x3(-x)3u → A21: (-x)3o3u → A213: (-x)3u3(-u) → A2132: x3(-u)3o → A21321: (-x)3(-x)3o ↳ A23: x3x3(-u) → A231 = A213 ↳ A232: u3(-x)3(-x) → A2321: (-u)3x3(-x) → A23212 = A21321 ↳ A3: o3u3(-x) → A32: u3(-u)3x → A321: (-u)3o3x → A3213 = A2321 ↳ A323 = A232 B: o3u3o → B2: u3(-u)3u → B21: (-u)3o3u → B213: (-u)3u3(-u) → B2132: o3(-u)3o ↳ B23: u3o3(-u) → B231 = B213 C: x3x3o → C1: (-x)3u3o → C12: x3(-u)3u → C121: (-x)3(-x)3u → C1213: (-x)3x3(-u) → C12132: o3(-x)3(-x) ↳ C123: x3o3(-u) → C1231 = C1213 ↳ C2: u3(-x)3x → C21: (-u)3x3x → C212 = C121 ↳ C213: (-u)3u3(-x) → C2132: o3(-u)3x → C21323 = C12132 ↳ C23: u3o3(-x) → C231 = C213
A priori invalid combinations:	B + A2,A21,A213,A2132,A21321,A23,A232,A2321,A32,A321 - i.e. only A,A3 + C12,C121,C1213,C12132,C123,C2,C21,C213,C2132,C23 - i.e. only C,C1 B2 + A,A21,A213,A2132,A21321,A23,A232,A2321,A3,A321 - i.e. only A2,A32 + C,C1,C121,C1213,C12132,C123,C21,C213,C2132,C23 - i.e. only C12,C2 B21 + A,A2,A213,A2132,A21321,A23,A232,A2321,A3,A32 - i.e. only A21,A321 + C,C1,C12,C1213,C12132,C123,C2,C213,C2132,C23 - i.e. only C121,C21 B213 + A,A2,A21,A2132,A21321,A23,A232,A3,A32,A321 - i.e. only A213,A2321 + C,C1,C12,C121,C12132,C123,C2,C21,C2132,C23 - i.e. only C1213,C213 B2132 + A,A2,A21,A213,A23,A232,A2321,A3,A32,A321 - i.e. only A2132,A21321 + C,C1,C12,C121,C1213,C123,C2,C21,C213,C23 - i.e. only C12132,C2132 B23 + A,A2,A21,A213,A2132,A21321,A2321,A3,A32,A321 - i.e. only A23,A232 + C,C1,C12,C121,C1213,C12132,C2,C21,C213,C2132 - i.e. only C123,C23
Other layer-combinations:	ABC oox 3 xux 3 xoo &#xt (self-inv) : itself ABC1 oo(-x) 3 xuu 3 xoo &#xt (inv = A3BC) A3BC1 oo(-x) 3 uuu 3 (-x)oo &#xt (self-inv) A2B2C12 xux 3 (-x)(-u)(-u) 3 uuu &#xt (inv = A32B2C2) A2B2C2 xuu 3 (-x)(-u)(-x) 3 uux &#xt (self-inv) : asks for corealmic cells with non-convex exterior blend A32B2C12 uux 3 (-u)(-u)(-u) 3 xuu &#xt (self-inv) A21B21C121 (-x)(-u)(-x) 3 oo(-x) 3 uuu &#xt (inv = A232B23C23) : asks for non-convex cell-join at inner layer A21B21C21 (-x)(-u)(-u) 3 oox 3 uux &#xt (inv = A23B23C23) : asks for non-convex cell-join at inner layer A321B21C121 (-u)(-u)(-x) 3 oo(-x) 3 xuu &#xt (inv = A232B23C123) A321B21C21 (-u)(-u)(-u) 3 oox 3 xux &#xt (inv = A23B23C123) A213B213C1213 (-x)(-u)(-x) 3 uux 3 (-u)(-u)(-u) &#xt (inv = A2321B213C213) : asks for non-convex cell-join at inner layer A213B213C213 (-x)(-u)(-u) 3 uuu 3 (-u)(-u)(-x) &#xt (self-inv) : asks for non-convex cell-join at inner layer A2321B213C1213 (-u)(-u)(-x) 3 xux 3 (-x)(-u)(-u) &#xt (self-inv) A2132B2132C12132 xoo 3 (-u)(-u)(-u) 3 oo(-x) &#xt (inv = A21321B2132C2132) : asks for non-convex cell-join at inner layer A2132B2132C2132 xoo 3 (-u)(-u)(-u) 3 oox &#xt (self-inv) : asks for non-convex cell-join at inner layer A21321B2132C12132 (-x)oo 3 (-x)(-u)(-u) 3 oo(-x) &#xt (self-inv)
Stott expansion: (derived potential CRFs)	-:ABC = 1133:A2321B213C1213: oox 3 xux 3 xoo &#xt = Wythoffian `o3x3x3o` (deca) with cell list: 10 tuts (itself)	1(-2):ABC1 = inv 112(-3):A321B21C121: xxo 3 oxx 3 xoo &#xt = Wythoffian `x3o3x3o` (srip) with cell list: 5 coes 5 octs 10 trips related: xx. 3 ox. 3 xo. &#x (coatut) → CRF (segmentochoron) with cell list: 1 co 4 octs 4 tricues (J3) 6 trips 1 tut related: .xo 3 .xx 3 .oo &#x (octatut) → CRF (segmentochoron) with cell list: 1 oct 4 tricues (J3) 4 trips 1 tut
	1(-2)3:A3BC1 = (-1)222(-3):A32B2C12: xxo 3 xxx 3 oxx &#xt (tutato gybcu) → CRF with cell list: 8 hips 8 tricues (J3) 12 trips 2 tuts related: xx. 3 xx. 3 ox. &#x (tutatoe) → CRF (segmentochoron) with cell list: 4 hips 1 toe 4 tricues (J3) 6 trips 1 tut	1(-2)(-2)3:A3BC1 = (-1)22(-3):A32B2C12: xxo 3 ooo 3 oxx &#xt = Wythoffian `x3o3o3x` (spid) with cell list: 10 tets 20 trips related: xx. 3 oo. 3 ox. &#x (tetaco) → CRF (segmentochoron) with cell list: 1 co 5 tets 10 trips
	22(-3):A2B2C12 = inv 111:A321B21C21: xux 3 xoo 3 xxx &#xt (coatotum) → CRF with cell list: 1 co 6 hips 1 toe 4 tricues (J3) 4 trips 4 tuts	22(-3)(-3):A2B2C12 = inv 11:A321B21C21: xux 3 xoo 3 ooo &#xt = Wythoffian `x3x3o3o` (tip) with cell list: 5 tets 5 tuts
	1221:A21321B2132C12132: oxx 3 xoo 3 xxo &#xt (tetaco altut) → CRF with cell list: 6 gybefs (J26) 4 octs 5 tets 4 tricues (J3) 4 trips 1 tut related: ox. 3 xo. 3 xx. &#x (coatut) → CRF (segmentochoron) with cell list: 1 co 4 octs 4 tricues (J3) 6 trips 1 tut related: .xx 3 .oo 3 .xo &#x (tetaco) → CRF (segmentochoron) with cell list: 1 co 5 tets 10 trips

in `. o2o3o` subsymmetry (up)
Representation:	oxuxo 2 xuxoo 3 ooxux &#xt (deca)
All layers & kaleido-facetings per layer:	A: o x3o → A2: o (-x)3x → A23: o o3(-x) B: x u3o → B1: (-x) u3o → B12: (-x) (-u)3u → B123: (-x) o3(-u) ↳ B2: x (-u)3u → B21 = B12 ↳ B23: x o3(-u) → B231 = B123 C: u x3x → C1: (-u) x3x → C12: (-u) (-x)3u → C123: (-u) x3(-u) → C1232: (-u) (-x)3(-x) ↳ C2: u (-x)3u → C21 = C12 ↳ C23 = u x3(-u) → C231 = C123 ↳ C232: u (-x)3(-x) → C2321 = C1232 ↳ C3: u u3(-x) → C31: (-u) u3(-x) → C312: (-u) (-u)3x → C3123 = C1232 ↳ C32 = u (-u)3x → C321 = C312 ↳ C323 = C232 D: x o3u → D1: (-x) o3u → D13: (-x) u3(-u) → D132: (-x) (-u)3o ↳ D3: x u3(-u) → D31= D13 ↳ D32: x (-u)3o → D321 = D132 E: o o3x → E3: o x3(-x) → E32: o (-x)3o
A priori invalid combinations:	A + B12,B123,B2,B23, i.e. only B,B1 A2 + B,B1,B123,B23, i.e. only B12,B2 A23 + B,B1,B12,B2, i.e. only B123,B23 B + C1,C12,C123,C1232,C2,C23,C232,C31,C312,C32, i.e. only C,C3 B1 + C,C12,C123,C1232,C2,C23,C232,C3,C312,C32, i.e. only C1,C31 B12 + C,C1,C123,C1232,C2,C23,C232,C3,C31,C32, i.e. only C12,C312 B123 + C,C1,C12,C2,C23,C232,C3,C31,C312,C32, i.e. only C123,C1232 B2 + C,C1,C12,C123,C1232,C23,C232,C3,C31,C312, i.e. only C2,C32 B23 + C,C1,C12,C123,C1232,C2,C3,C31,C312,C32, i.e. only C23,C232 C + D1,D13,D132,D3,D32, i.e. only D C1 + D,D13,D132,D3,D32, i.e. only D1 C12 + D,D13,D132,D3,D32, i.e. only D1 C123 + D,D1,D132,D3,D32, i.e. only D13 C1232 + D,D1,D13,D3,D32, i.e. only D132 C2 + D1,D13,D132,D3,D32, i.e. only D C23 + D,D1,D13,D132,D32, i.e. only D3 C232 + D,D1,D13,D132,D3, i.e. only D32 C3 + D,D1,D13,D132,D32, i.e. only D3 C31 + D,D1,D132,D3,D32, i.e. only D13 C312 + D,D1,D13,D3,D32, i.e. only D132 C32 + D,D1,D13,D132,D3, i.e. only D32 D + E3,E32, i.e. only E D1 + E3,E32, i.e. only E D13 + E,E32, i.e. only E3 D132 + E,E3, i.e. only E32 D3 + E,E32, i.e. only E3 D32 + E,E3, i.e. only E32
Other layer-combinations:	ABCDE oxuxo 2 xuxoo 3 ooxux &#xt : (self-inv) → itself ABC3D3E3 oxuxo 2 xuuux 3 oo(-x)(-u)(-x) &#xt : (inv = A2B2C2DE) → ‡ AB1C1D1E o(-x)(-u)(-x)o 2 xuxoo 3 ooxux &#xt : (self-inv) → ‡ AB1C31D13E3 o(-x)(-u)(-x)o 2 xuuux 3 oo(-x)(-u)(-x) &#xt : (inv = A2B12C12D1E) → ‡ A2B12C312D132E32 o(-x)(-u)(-x)o 2 (-x)(-u)(-u)(-u)(-x) 3 xuxoo &#xt : (inv = A23B123C123D13E3) → ‡ A23B123C1232D132E32 o(-x)(-u)(-x)o 2 oo(-x)(-u)(-x) 3 (-x)(-u)(-x)oo &#xt : (self-inv) → ‡ A23B23C23D3E3 oxuxo 2 ooxux 3 (-x)(-u)(-u)(-u)(-x) &#xt : (inv = A2B2C32D32E32) A23B23C232D32E32 oxuxo 2 oo(-x)(-u)(-x) 3 (-x)(-u)(-x)oo &#xt : (self-inv) → ‡
Stott expansion: (derived potential CRFs)	22:A23B23C23D3E3: oxuxo 2 ooxux 3 xooox &#xt : itself non-convex, but dissectable into related: ox... 2 oo... 3 xo... &#x = Wythoffian `x3o3o3o` (pen) with cell list: 5 tet related: .xuxo 2 .oxux 3 .ooox &#xt = Wythoffian `x3x3o3o` (tip) with cell list: 5 tet 5 tut

EKF of the small prismatodecachoron (`x3o3o3x`)

©

(As it will turn out, the set of resulting polychora in . o3o3o here is identical to those which turn up from the corresponding consideration of srip wrt. this subsymmetry.)

in `. o3o3o` subsymmetry (up)
Representation:	xxo 3 ooo 3 oxx &#xt (spid)
All layers & kaleido-facetings per layer:	A: x3o3o → A1: (-x)3 x 3 o → A12: o 3(-x)3 x → A123: o 3 o 3(-x) B: x3o3x → B1: (-x)3 x 3 x → B12: o 3(-x)3 u ↳ B13: (-x)3 u 3(-x) ↳ B3: x 3 x 3(-x) → (B31 = B13) ↳ B32: u 3(-x)3 o C: o3o3x → C3: o 3 x 3(-x) → C32: x 3(-x)3 o → C321: (-x)3 o 3 o
A priori invalid combinations:	A + B1,B12,B13 A1 + B,B3,B12,B32 A1 + C32 A12 + B1,B3,B13,B32 A12 + C3 A123 + B,B1,B12,B13,B32 A123 + C B + C3,C321 B1 + C3,C32 B3 + C,C32,C321 B12 + C3,C32,C321 B13 + C,C32,C321 B32 + C,C3,C321
Other layer-combinations:	A1B1: (-x)(-x)o 3 xxo 3 oxx &#xt A12: oxo 3 (-x)oo 3 xxx &#xt → †) A12B12: ooo 3 (-x)(-x)o 3 xux &#xt A12C32: oxx 3 (-x)o(-x) 3 xxo &#xt → †) A123B3C3: oxo 3 oxx 3 (-x)(-x)(-x) &#xt → †) A1B13C3: (-x)(-x)o 3 xux 3 o(-x)(-x) &#xt
Stott expansion: (derived potential CRFs)	1:A1B1: oox 3 xxo 3 oxx &#xt = Wythoffian `x3o3x3o` (srip) with cell list: 5 coes 5 octs 10 trips related: .ox 3 .xo 3 .xx &#x (coatut) → CRF (segmentochoron) with cell list: 1 co 4 octs 4 tricues (J3) 6 trips 1 tut related: oo. 3 xx. 3 ox. &#x (octatut) → CRF (segmentochoron) with cell list: 1 oct 4 tricues (J3) 4 trips 1 tut	2:-: xxo 3 xxx 3 oxx &#xt (tutatoe gybcu) → CRF with cell list: 8 hips 8 tricues (J3) 12 trips 2 tuts (bistratic segmentochoral stack) related: xx. 3 xx. 3 ox. &#x (tutatoe) → CRF (segmentochoron) with cell list: 4 hips 1 toe 4 tricues (J3) 6 trips 1 tut
Stott expansion: (derived potential CRFs)	2:A12B12: ooo 3 oox 3 xux &#xt = Wythoffian `x3x3o3o` (tip) with cell list: 5 tets 5 tuts	13:A1B13C3: xoo 3 xux 3 oox &#xt = Wythoffian `o3x3x3o` (deca) with cell list: 10 tuts

in `. o2o3o` subsymmetry (up)
Representation:	x(ou)x 2 x(xo)o 3 o(xo)x &#xt (spid)
All layers & kaleido-facetings per layer:	A: x2x3o → A1: (-x)2 x 3 o → A12: (-x)2(-x)3 x → A123: (-x)2 o 3(-x) ↳ A2: x 2(-x)3 x → (A21 = A12) ↳ A23: x 2 o 3(-x) → (A231 = A123) B: o2x3x → B2: o 2(-x)3 u ↳ B3: o 2 u 3(-x) C: u2o3o D: x2o3x → D1: (-x)2 o 3 x → D13: (-x)2 x 3(-x) → D132: (-x)2(-x)3 o ↳ D3: x 2 x 3(-x) → (D31 = D13) ↳ D32: x 2(-x)3 o → (D321 = D132)
A priori invalid combinations:	A + B2,D1,D13,D32,D132 A1 + B2,D,D3,D32,D132 A2 + B,B3,D1,D3,D13,D132 A12 + B,B3,D,D3,D13,D32 A23 + B,D,D1,D13,D132 A123 + B,D,D1,D3,D32 B + D3,D13,D32,D132 B2 + D3,D13 B3 + D,D1
Other layer-combinations:	B3D3 x(ou)x 2 x(uo)x 3 o((-x)o)(-x) &#xt A1D1 (-x)(ou)(-x) 2 x(xo)o 3 o(xo)x &#xt → † A1B3D13 (-x)(ou)(-x) 2 x(uo)x 3 o((-x)o)(-x) &#xt → † A2B2D32 x(ou)x 2 (-x)((-x)o)(-x) 3 x(uo)o &#xt → † A12B2D132 (-x)(ou)(-x) 2 (-x)((-x)o)(-x) 3 x(uo)o &#xt → † A23B2D32 x(ou)x 2 o((-x)o)(-x) 3 (-x)(uo)o &#xt → † A123B2D132 (-x)(ou)(-x) 2 o((-x)o)(-x) 3 (-x)(uo)o &#xt → †
Stott expansion: (derived potential CRFs)	3:B3D3: x(ou)x 2 x(uo)x 3 x(ox)o &#xt (biscsrip) → CRF with cell list: 3 coes 1 hip 2 oct 3 squippies (J1) 2 tricues (J3) 7 trips

EKF of the rectified hexacosachoron (`o3x3o5o`)

©

in `o2o3o5o` subsymmetry (up)
Representation:	DCBAVFfxoo 2 xoxFofofVx 3 oxoofoxxoo 5 ooxooxxoof &#zx (rox)
All layers & kaleido-facetings per layer:	A: D2x3o5o → A2: D2(-x)3x5o → A23: D2o3(-x)5f B: C2o3x5o → B3: C2x3(-x)5f → B32: C2(-x)3o5f C: B2x3o5x → C2: B2(-x)3x5x → C23: B2o3(-x)5F ↳ C24: B2(-x)3F5(-x) ↳ C4: B2x3f5(-x) → (C42 = C24) D: A2F3o5o E: V2o3f5o F: F2f3o5x → F4: F2f3f5(-x) G: f2o3x5x → G3: f2x3(-x)5F → G32: f2(-x)3o5F ↳ G4: f2o3F5(-x) H: x2f3x5o → H1: (-x)2f3x5o → H13: (-x)2F3(-x)5f ↳ H3: x2F3(-x)5f → (H31 = H13) I: o2V3o5o i: o2x3o5f → i2: o2(-x)3x5f → i23: o2o3(-x)5V (Note, I and i both belong to the same hyperplane o2... .)
A priori invalid combinations:	A + B32, C2, C24, G32, i2 A2 + B3, C, C4, C23, G3, H3, H13, i, i23 A23 + B, C2, G, H, H1, i2 B + C23, G3, H3, H13, i23 B3 + C2, C24, G, G32, H, H1, i2 B32 + C, C4, G3, i C + F4, G4, G32, i2 C2 + F4, G3, G4, H3, H13, i, i23 C4 + F, G, G32, i2 C23 + G, H, H1, i2 C24 + F, G, G3, i F + G4 F4 + G G + H3, H13, i23 G3 + H, H1, i2 G32 + i H + i23 H1 + i23 H3 + i2 H13 + i2 (all these would provide u edges (→ ‡); thus reducing from 4320 to 70 potential combinations only)
Other layer-combinations:	H1: DCBAVFf(-x)oo 2 xoxFofofVx 3 oxoofoxxoo 5 ooxooxxoof &#zx → †) (dead end at I) C4F4G4: DCBAVFfxoo 2 xoxFofofVx 3 oxfoffFxoo 5 oo(-x)oo(-x)(-x)oof &#zx → ‡ (f in C, E, F) C4F4G4H1: DCBAVFf(-x)oo 2 xoxFofofVx 3 oxfoffFxoo 5 oo(-x)oo(-x)(-x)oof &#zx → †) B3G3H3: DCBAVFfxoo 2 xxxFofxFVx 3 o(-x)oofo(-x)(-x)oo 5 ofxooxFfof &#zx → ‡ (f in G, i) B3G3H3i23: DCBAVFfxoo 2 xxxFofxFVo 3 o(-x)oofo(-x)(-x)o(-x) 5 ofxooxFfoV &#zx B3G3H13: DCBAVFf(-x)oo 2 xxxFofxFVx 3 o(-x)oofo(-x)(-x)oo 5 ofxooxFfof &#zx → †) (dead end at I) B3G3H13i23: DCBAVFf(-x)oo 2 xxxFofxFVo 3 o(-x)oofo(-x)(-x)o(-x) 5 ofxooxFfoV &#zx → †) (dead end at I) B3C4F4G3H3: DCBAVFfxoo 2 xxxFofxFVx 3 o(-x)foff(-x)(-x)oo 5 of(-x)oo(-x)Ffof &#zx → †) B3C4F4G3H3i23: DCBAVFfxoo 2 xxxFofxFVo 3 o(-x)foff(-x)(-x)o(-x) 5 of(-x)oo(-x)FfoV &#zx → †) B3C4F4G3H13: DCBAVFf(-x)oo 2 xxxFofxFVx 3 o(-x)foff(-x)(-x)oo 5 of(-x)oo(-x)Ffof &#zx → †) B3C4F4G3H13i23: DCBAVFf(-x)oo 2 xxxFofxFVo 3 o(-x)foff(-x)(-x)o(-x) 5 of(-x)oo(-x)FfoV &#zx → †) B3C4F4G4H3: DCBAVFfxoo 2 xxxFofoFVx 3 o(-x)foffF(-x)oo 5 of(-x)oo(-x)(-x)fof &#zx → †) B3C4F4G4H3i23: DCBAVFfxoo 2 xxxFofoFVo 3 o(-x)foffF(-x)o(-x) 5 of(-x)oo(-x)(-x)foV &#zx → †) B3C4F4G4H13: DCBAVFf(-x)oo 2 xxxFofoFVx 3 o(-x)foffF(-x)oo 5 of(-x)oo(-x)(-x)fof &#zx → †) B3C4F4G4H13i23: DCBAVFf(-x)oo 2 xxxFofoFVo 3 o(-x)foffF(-x)o(-x) 5 of(-x)oo(-x)(-x)foV &#zx → †) B3C23G3H3: DCBAVFfxoo 2 xxoFofxFVx 3 o(-x)(-x)ofo(-x)(-x)oo 5 ofFooxFfof &#zx → †) B3C23G3H3i23: DCBAVFfxoo 2 xxoFofxFVo 3 o(-x)(-x)ofo(-x)(-x)o(-x) 5 ofFooxFfoV &#zx → †) B3C23G3H13: DCBAVFf(-x)oo 2 xxoFofxFVx 3 o(-x)(-x)ofo(-x)(-x)oo 5 ofFooxFfof &#zx → †) B3C23G3H13i23: DCBAVFf(-x)oo 2 xxoFofxFVo 3 o(-x)(-x)ofo(-x)(-x)o(-x) 5 ofFooxFfoV &#zx → †) A2C2i2: DCBAVFfxoo 2 (-x)o(-x)FofofV(-x) 3 xxxofoxxox 5 ooxooxxoof &#zx → †) (dead end at D) A2C2H1i2: DCBAVFf(-x)oo 2 (-x)o(-x)FofofV(-x) 3 xxxofoxxox 5 ooxooxxoof &#zx → †) A2C2G32i2: DCBAVFfxoo 2 (-x)o(-x)Fof(-x)fV(-x) 3 xxxofooxox 5 ooxooxFoof &#zx → †) A2C2G32H1i2: DCBAVFf(-x)oo 2 (-x)o(-x)Fof(-x)fV(-x) 3 xxxofooxox 5 ooxooxFoof &#zx → †) A2C24F4G4i2: DCBAVFfxoo 2 (-x)o(-x)FofofV(-x) 3 xxFoffFxox 5 oo(-x)oo(-x)(-x)oof &#zx → †) (dead end at D) A2C24F4G4H1i2: DCBAVFf(-x)oo 2 (-x)o(-x)FofofV(-x) 3 xxFoffFxox 5 oo(-x)oo(-x)(-x)oof &#zx → †) (dead end at D) A2C24F4G32i2: DCBAVFfxoo 2 (-x)o(-x)Fof(-x)fV(-x) 3 xxFoffoxox 5 oo(-x)oo(-x)Foof &#zx → †) (dead end at D) A2C24F4G32H1i2: DCBAVFf(-x)oo 2 (-x)o(-x)Fof(-x)fV(-x) 3 xxFoffoxox 5 oo(-x)oo(-x)Foof &#zx → †) (dead end at D) A2B32C2i2: DCBAVFfxoo 2 (-x)(-x)(-x)FofofV(-x) 3 xoxofoxxox 5 ofxooxxoof &#zx → †) (dead end at D) A2B32C2H1i2: DCBAVFf(-x)oo 2 (-x)(-x)(-x)FofofV(-x) 3 xoxofoxxox 5 ofxooxxoof &#zx → †) (dead end at D) A2B32C2G32i2: DCBAVFfxoo 2 (-x)(-x)(-x)Fof(-x)fV(-x) 3 xoxofooxox 5 ofxooxFoof &#zx → †) (dead end at D) A2B32C2G32H1i2: DCBAVFf(-x)oo 2 (-x)(-x)(-x)Fof(-x)fV(-x) 3 xoxofooxox 5 ofxooxFoof &#zx → †) (dead end at D) A2B32C24F4G4i2: DCBAVFfxoo 2 (-x)(-x)(-x)FofofV(-x) 3 xoFoffFxox 5 of(-x)oo(-x)(-x)oof &#zx → †) A2B32C24F4G4H1i2: DCBAVFf(-x)oo 2 (-x)(-x)(-x)FofofV(-x) 3 xoFoffFxox 5 of(-x)oo(-x)(-x)oof &#zx → †) A2B32C24F4G32i2: DCBAVFfxoo 2 (-x)(-x)(-x)Fof(-x)fV(-x) 3 xoFoffoxox 5 of(-x)oo(-x)Foof &#zx → †) A2B32C24F4G32H1i2: DCBAVFf(-x)oo 2 (-x)(-x)(-x)Fof(-x)fV(-x) 3 xoFoffoxox 5 of(-x)oo(-x)Foof &#zx → †) A23B3G3H3: DCBAVFfxoo 2 oxxFofxFVx 3 (-x)(-x)oofo(-x)(-x)oo 5 ffxooxFfof &#zx → ‡ (f in A) A23B3G3H3i23: DCBAVFfxoo 2 oxxFofxFVo 3 (-x)(-x)oofo(-x)(-x)o(-x) 5 ffxooxFfoV &#zx → ‡ (f in A) A23B3G3H13: DCBAVFf(-x)oo 2 oxxFofxFVx 3 (-x)(-x)oofo(-x)(-x)oo 5 ffxooxFfof &#zx → ‡ (f in A) A23B3G3H13i23: DCBAVFf(-x)oo 2 oxxFofxFVo 3 (-x)(-x)oofo(-x)(-x)o(-x) 5 ffxooxFfoV &#zx → ‡ (f in A) A23B3C4F4G3H3: DCBAVFfxoo 2 oxxFofxFVx 3 (-x)(-x)foff(-x)(-x)oo 5 ff(-x)oo(-x)Ffof &#zx → ‡ (F in A) A23B3C4F4G3H3i23: DCBAVFfxoo 2 oxxFofxFVo 3 (-x)(-x)foff(-x)(-x)o(-x) 5 ff(-x)oo(-x)FfoV &#zx → ‡ (F in A) A23B3C4F4G3H13: DCBAVFf(-x)oo 2 oxxFofxFVx 3 (-x)(-x)foff(-x)(-x)oo 5 ff(-x)oo(-x)Ffof &#zx → ‡ (F in A) A23B3C4F4G3H13i23: DCBAVFf(-x)oo 2 oxxFofxFVo 3 (-x)(-x)foff(-x)(-x)o(-x) 5 ff(-x)oo(-x)FfoV &#zx → ‡ (F in A) A23B3C4F4G4H3: DCBAVFfxoo 2 oxxFofoFVx 3 (-x)(-x)foffF(-x)oo 5 ff(-x)oo(-x)(-x)fof &#zx → ‡ (F in A) A23B3C4F4G4H3i23: DCBAVFfxoo 2 oxxFofoFVo 3 (-x)(-x)foffF(-x)o(-x) 5 ff(-x)oo(-x)(-x)foV &#zx → ‡ (F in A) A23B3C4F4G4H13: DCBAVFf(-x)oo 2 oxxFofoFVx 3 (-x)(-x)foffF(-x)oo 5 ff(-x)oo(-x)(-x)fof &#zx → ‡ (F in A) A23B3C4F4G4H13i23: DCBAVFf(-x)oo 2 oxxFofoFVo 3 (-x)(-x)foffF(-x)o(-x) 5 ff(-x)oo(-x)(-x)foV &#zx → ‡ (F in A) A23B3C23G3H3: DCBAVFfxoo 2 oxoFofxFVx 3 (-x)(-x)(-x)ofo(-x)(-x)oo 5 ffFooxFfof &#zx → ‡ (f in A) A23B3C23G3H3i23: DCBAVFfxoo 2 oxoFofxFVo 3 (-x)(-x)(-x)ofo(-x)(-x)o(-x) 5 ffFooxFfoV &#zx → ‡ (f in A) A23B3C23G3H13: DCBAVFf(-x)oo 2 oxoFofxFVx 3 (-x)(-x)(-x)ofo(-x)(-x)oo 5 ffFooxFfof &#zx → ‡ (f in A) A23B3C23G3H13i23: DCBAVFf(-x)oo 2 oxoFofxFVo 3 (-x)(-x)(-x)ofo(-x)(-x)o(-x) 5 ffFooxFfoV &#zx → ‡ (f in A) A23B3C23F4G3H3: DCBAVFfxoo 2 oxoFofxFVx 3 (-x)(-x)(-x)off(-x)(-x)oo 5 ffFoo(-x)Ffof &#zx → ‡ (F in A) A23B3C23F4G3H3i23: DCBAVFfxoo 2 oxoFofxFVo 3 (-x)(-x)(-x)off(-x)(-x)o(-x) 5 ffFoo(-x)FfoV &#zx → ‡ (F in A) A23B3C23F4G3H13: DCBAVFf(-x)oo 2 oxoFofxFVx 3 (-x)(-x)(-x)off(-x)(-x)oo 5 ffFoo(-x)Ffof &#zx → ‡ (F in A) A23B3C23F4G3H13i23: DCBAVFf(-x)oo 2 oxoFofxFVo 3 (-x)(-x)(-x)off(-x)(-x)o(-x) 5 ffFoo(-x)FfoV &#zx → ‡ (F in A) A23B3C23F4G4H3: DCBAVFfxoo 2 oxoFofoFVx 3 (-x)(-x)(-x)offF(-x)oo 5 ffFoo(-x)(-x)fof &#zx → ‡ (F in A) A23B3C23F4G4H3i23: DCBAVFfxoo 2 oxoFofoFVo 3 (-x)(-x)(-x)offF(-x)o(-x) 5 ffFoo(-x)(-x)foV &#zx → ‡ (F in A) A23B3C23F4G4H13: DCBAVFf(-x)oo 2 oxoFofoFVx 3 (-x)(-x)(-x)offF(-x)oo 5 ffFoo(-x)(-x)fof &#zx → ‡ (F in A) A23B3C23F4G4H13i23: DCBAVFf(-x)oo 2 oxoFofoFVo 3 (-x)(-x)(-x)offF(-x)o(-x) 5 ffFoo(-x)(-x)foV &#zx → ‡ (F in A) A23B32C23G32H3i23: DCBAVFfxoo 2 o(-x)oFof(-x)FVo 3 (-x)o(-x)ofoo(-x)o(-x) 5 ffFooxFfoV &#zx → ‡ (f in A) A23B32C23G32H13i23: DCBAVFf(-x)oo 2 o(-x)oFof(-x)FVo 3 (-x)o(-x)ofoo(-x)o(-x) 5 ffFooxFfoV &#zx → ‡ (f in A) A23B32C23F4G4H3i23: DCBAVFfxoo 2 o(-x)oFofoFVo 3 (-x)o(-x)offF(-x)o(-x) 5 ffFoo(-x)(-x)foV &#zx → ‡ (F in A) A23B32C23F4G4H13i23: DCBAVFf(-x)oo 2 o(-x)oFofoFVo 3 (-x)o(-x)offF(-x)o(-x) 5 ffFoo(-x)(-x)foV &#zx → ‡ (F in A) A23B32C23F4G32H3i23: DCBAVFfxoo 2 o(-x)oFof(-x)FVo 3 (-x)o(-x)offo(-x)o(-x) 5 ffFoo(-x)FfoV &#zx → ‡ (F in A) A23B32C23F4G32H13i23: DCBAVFf(-x)oo 2 o(-x)oFof(-x)FVo 3 (-x)o(-x)offo(-x)o(-x) 5 ffFoo(-x)FfoV &#zx → ‡ (F in A) A23B32C24F4G4H3i23: DCBAVFfxoo 2 o(-x)(-x)FofoFVo 3 (-x)oFoffF(-x)o(-x) 5 ff(-x)oo(-x)(-x)foV &#zx → ‡ (F in A) A23B32C24F4G4H13i23: DCBAVFf(-x)oo 2 o(-x)(-x)FofoFVo 3 (-x)oFoffF(-x)o(-x) 5 ff(-x)oo(-x)(-x)foV &#zx → ‡ (F in A) A23B32C24F4G32H3i23: DCBAVFfxoo 2 o(-x)(-x)Fof(-x)FVo 3 (-x)oFoffo(-x)o(-x) 5 ff(-x)oo(-x)FfoV &#zx → ‡ (F in A) A23B32C24F4G32H13i23: DCBAVFf(-x)oo 2 o(-x)(-x)Fof(-x)FVo 3 (-x)oFoffo(-x)o(-x) 5 ff(-x)oo(-x)FfoV &#zx → ‡ (F in A)
Stott expansion: (derived CRFs)	3:B3G3H3i23: DCBAVFfxoo 2 xxxFofxFVo 3 xoxxFxooxo 5 ofxooxFfoV &#zx → CRF with cell list: 30 ids 120 octs 60 pips 48 pocuroes (J32) 60 squippies (J1) 220 tets 40 thawroes (J92) 2 ties 80 tricues (J3) 120 trips related: ..BAVFfxoo 2 ..xFofxFVo 3 ..xxFxooxo 5 ..xooxFfoV &#zx → CRF with cell list: 2 grids 30 ids 120 octs 24 pecues (J5) 24 pocuroes (J32) 60 squippies (J1) 220 tets 40 thawroes (J92) 120 trips
in `. o3o5o` subsymmetry (up)
additional, not prismatically symmetric combinations of formers:	none (As there are just 2 symmetrical combinations - rox and that single CRF - which differ in their equatorial sections there is no further combination of resp. hemiglomes either.)
using here node marks / (pseudo) edge lengths: `F=f+x=ff, V=F+v=2f, A=F+x=f+2x, B=V+x=2f+x=fff, C=2F=2f+2x, D=F+V=3f+x`

in `o3o3o *b3o` subsymmetry (up)
Representation:	Voo\|Fxf\|ofx 3 xxx\|ooo\|fff 3 oVo\|fFx\|xof *b3 ooV\|xfF\|fxo &#zx (rox) with cyclical layer symmetries: A(134) → B(341) → C(413) → A(134) C(134) → D(341) → E(413) → C(134) G(134) → H(341) → I(413) → G(134)
All layers & kaleido-facetings per layer:	A: V3x3o b3o → A2: B3(-x)3x b3x → A23: B3o3(-x) b3x → A234: B3x3(-x) b3(-x) → A2342: C3(-x)3o b3o ↳ A24: B3o3x b3(-x) → (A243.. = A234..) B: o3x3V b3o → B2: x3(-x)3B b3x → B21: (-x)3o3B b3x → B214: (-x)3x3B b3(-x) → B2142: o3(-x)3C b3o ↳ B24: x3o3B b3(-x) → (B241.. = B214..) C: o3x3o b3V → C2: x3(-x)3x b3B → C21: (-x)3o3x b3B → C213: (-x)3x3(-x) b3B → C2132: o3(-x)3o b3C ↳ C23: x3o3(-x) b3B → (C231.. = C213..) D: F3o3f b3x → D4: F3x3f b3(-x) → D42: A3(-x)3F b3o E: x3o3F b3f → E1: (-x)3x3F b3f → E12: o3(-x)3A b3F F: f3o3x b3F → F3: f3x3(-x) b3F → F32: F3(-x)3o b3A G: o3f3x b3f → G3: o3F3(-x) b3f H: f3f3o b3x → H4: f3F3o b3(-x) I: x3f3f b3o → I1: (-x)3F3f *b3o
A priori invalid combinations:	A + B2, B2142, C2, C2132, D42, E12, F32 A2 + B, B214, B24, C, C213, C23, D4, E1, F3, G3, H4 A23 + B214, B24, C2, C21, D4, F, G, H4 A234 + B2, B21, B2142, C2, C21, C2132, D, D42, E12, F, G, H A2342 + B, B214, C, C213, D4, E1, F3 A24 + B2, B21, C213, C23, D, F3, G3, H B + C2, C2132, D42, E12, F32 B2 + C, C21, C213, D4, E1, F3, H4, I1 B21 + C2, C23, D4, E, H4, I B214 + C2, C2132, C23, D, D42, E, E12, F32, H, I B2142 + C, C213, D4, E1, F3 B24 + C21, C213, D, E1, H, I1 C + D42, E12, F32 C2 + D4, E1, F3, G3, I1 C21 + E, F3, G3, I C213 + D42, E, E12, F, F32, G, I C2132 + D4, E1, F3 C23 + E1, F, G, I1	D + H4 D4 + E12, F32, H D42 + E1, F3 E + I1 E1 + F32, I E12 + F3 F + G3 F3 + G (all these would provide u edges (→ ‡); thus reducing from 46655 to 175 other potential combinations only)
Other layer-combinations:	ABCDEF3G3HI: VooFxfofx3xxxooxFff3oVofF(-x)(-x)of b3ooVxfFfxo&#zx → ‡ (f in D) ABCDE1F3G3HI1: VooF(-x)fof(-x)3xxxxoxFfF3oVofF(-x)(-x)of b3ooVxfFfxo&#zx → † ABCD4E1F3G3H4I1: VooF(-x)fof(-x)3xxxxxxFFF3oVofF(-x)(-x)of b3ooV(-x)fFf(-x)o&#zx → † ABC21DE1FGHI1: Vo(-x)F(-x)fof(-x)3xxooxoffF3oVxfFxxof b3ooBxfFfxo&#zx → † ABC21D4E1FGH4I1: Vo(-x)F(-x)fof(-x)3xxoxxofFF3oVxfFxxof b3ooB(-x)fFf(-x)o&#zx → † ABC213DE1F3G3HI1: Vo(-x)F(-x)fof(-x)3xxxoxxFfF3oV(-x)fF(-x)(-x)of b3ooBxfFfxo&#zx → † ABC213D4E1F3G3H4I1: Vo(-x)F(-x)fof(-x)3xxxxxxFFF3oV(-x)fF(-x)(-x)of b3ooB(-x)fFf(-x)o&#zx → † ABC23DEF3G3HI: VoxFxfofx3xxoooxFff3oV(-x)fF(-x)(-x)of b3ooBxfFfxo&#zx → ‡ (f in D) ABC23D4EF3G3H4I: VoxFxfofx3xxoxoxFFf3oV(-x)fF(-x)(-x)of b3ooB(-x)fFf(-x)o&#zx → † AB21C21DE1FGHI1: V(-x)(-x)F(-x)fof(-x)3xoooxoffF3oBxfFxxof b3oxBxfFfxo&#zx → † AB21C213DE1F3G3HI1: V(-x)(-x)F(-x)fof(-x)3xoxoxxFfF3oB(-x)fF(-x)(-x)of b3oxBxfFfxo&#zx → † AB214CD4E1FGH4I1: V(-x)oF(-x)fof(-x)3xxxxxofFF3oBofFxxof b3o(-x)V(-x)fFf(-x)o&#zx → † AB214CD4E1F3G3H4I1: V(-x)oF(-x)fof(-x)3xxxxxxFFF3oBofF(-x)(-x)of b3o(-x)V(-x)fFf(-x)o&#zx → † AB214C21D4E1FGH4I1: V(-x)(-x)F(-x)fof(-x)3xxoxxofFF3oBxfFxxof b3o(-x)B(-x)fFf(-x)o&#zx → † AB214C213D4E1F3G3H4I1: V(-x)(-x)F(-x)fof(-x)3xxxxxxFFF3oB(-x)fF(-x)(-x)of b3o(-x)B(-x)fFf(-x)o&#zx → † AB24C23D4EF3G3H4I: VxxFxfofx3xooxoxFFf3oB(-x)fF(-x)(-x)of b3o(-x)B(-x)fFf(-x)o&#zx → † A2B2C2DEFGHI: BxxFxfofx3(-x)(-x)(-x)ooofff3xBxfFxxof b3xxBxfFfxo&#zx A2B2C2DEF32GHI: BxxFxFofx3(-x)(-x)(-x)oo(-x)fff3xBxfFoxof b3xxBxfAfxo&#zx → † A2B2C2DE12F32GHI: BxxFoFofx3(-x)(-x)(-x)o(-x)(-x)fff3xBxfAoxof b3xxBxFAfxo&#zx → † A2B2C2D42E12F32GHI: BxxAoFofx3(-x)(-x)(-x)(-x)(-x)(-x)fff3xBxFAoxof b3xxBoFAfxo&#zx → † A2B2C2132DEFGHI: BxoFxfofx3(-x)(-x)(-x)ooofff3xBofFxxof b3xxCxfFfxo&#zx → † A2B2C2132DEF32GHI: BxoFxFofx3(-x)(-x)(-x)oo(-x)fff3xBofFoxof b3xxCxfAfxo&#zx → † A2B2C2132DE12FGHI: BxoFofofx3(-x)(-x)(-x)o(-x)offf3xBofAxxof b3xxCxFFfxo&#zx → † A2B2C2132DE12F32GHI: BxoFoFofx3(-x)(-x)(-x)o(-x)(-x)fff3xBofAoxof b3xxCxFAfxo&#zx → † A2B2C2132D42EFGHI: BxoAxfofx3(-x)(-x)(-x)(-x)oofff3xBoFFxxof b3xxCofFfxo&#zx → † A2B2C2132D42EF32GHI: BxoAxFofx3(-x)(-x)(-x)(-x)o(-x)fff3xBoFFoxof b3xxCofAfxo&#zx → † A2B2C2132D42E12FGHI: BxoAofofx3(-x)(-x)(-x)(-x)(-x)offf3xBoFAxxof b3xxCoFFfxo&#zx → † A2B2C2132D42E12F32GHI: BxoAoFofx3(-x)(-x)(-x)(-x)(-x)(-x)fff3xBoFAoxof b3xxCoFAfxo&#zx → † A2B21C21DE12FGHI1: B(-x)(-x)Fofof(-x)3(-x)ooo(-x)offF3xBxfAxxof b3xxBxFFfxo&#zx → † A2B21C21DE12F32GHI1: B(-x)(-x)FoFof(-x)3(-x)ooo(-x)(-x)ffF3xBxfAoxof b3xxBxFAfxo&#zx → † A2B21C21D42E12FGHI1: B(-x)(-x)Aofof(-x)3(-x)oo(-x)(-x)offF3xBxFAxxof b3xxBoFFfxo&#zx → † A2B21C21D42E12F32GHI1: B(-x)(-x)AoFof(-x)3(-x)oo(-x)(-x)(-x)ffF3xBxFAoxof b3xxBoFAfxo&#zx → † A2B21C2132DE12FGHI1: B(-x)oFofof(-x)3(-x)o(-x)o(-x)offF3xBofAxxof b3xxCxFFfxo&#zx → † A2B21C2132DE12F32GHI1: B(-x)oFoFof(-x)3(-x)o(-x)o(-x)(-x)ffF3xBofAoxof b3xxCxFAfxo&#zx → † A2B21C2132D42E12FGHI1: B(-x)oAofof(-x)3(-x)o(-x)(-x)(-x)offF3xBoFAxxof b3xxCoFFfxo&#zx → † A2B21C2132D42E12F32GHI1: B(-x)oAoFof(-x)3(-x)o(-x)(-x)(-x)(-x)ffF3xBoFAoxof b3xxCoFAfxo&#zx → † A2B2142C2DEFGHI: BoxFxfofx3(-x)(-x)(-x)ooofff3xCxfFxxof b3xoBxfFfxo&#zx → † A2B2142C2DEF32GHI: BoxFxFofx3(-x)(-x)(-x)oo(-x)fff3xCxfFoxof b3xoBxfAfxo&#zx → † A2B2142C2DE12FGHI: BoxFofofx3(-x)(-x)(-x)o(-x)offf3xCxfAxxof b3xoBxFFfxo&#zx → † A2B2142C2DE12F32GHI: BoxFoFofx3(-x)(-x)(-x)o(-x)(-x)fff3xCxfAoxof b3xoBxFAfxo&#zx → † A2B2142C2D42EFGHI: BoxAxfofx3(-x)(-x)(-x)(-x)oofff3xCxFFxxof b3xoBofFfxo&#zx → † A2B2142C2D42EF32GHI: BoxAxFofx3(-x)(-x)(-x)(-x)o(-x)fff3xCxFFoxof b3xoBofAfxo&#zx → † A2B2142C2D42E12FGHI: BoxAofofx3(-x)(-x)(-x)(-x)(-x)offf3xCxFAxxof b3xoBoFFfxo&#zx → † A2B2142C2D42E12F32GHI: BoxAoFofx3(-x)(-x)(-x)(-x)(-x)(-x)fff3xCxFAoxof b3xoBoFAfxo&#zx → † A2B2142C21DE12FGHI1: Bo(-x)Fofof(-x)3(-x)(-x)oo(-x)offF3xCxfAxxof b3xoBxFFfxo&#zx → † A2B2142C21DE12F32GHI1: Bo(-x)FoFof(-x)3(-x)(-x)oo(-x)(-x)ffF3xCxfAoxof b3xoBxFAfxo&#zx → † A2B2142C21D42E12FGHI1: Bo(-x)Aofof(-x)3(-x)(-x)o(-x)(-x)offF3xCxFAxxof b3xoBoFFfxo&#zx → † A2B2142C21D42E12F32GHI1: Bo(-x)AoFof(-x)3(-x)(-x)o(-x)(-x)(-x)ffF3xCxFAoxof b3xoBoFAfxo&#zx → † A2B2142C2132DEFGHI: BooFxfofx3(-x)(-x)(-x)ooofff3xCofFxxof b3xoCxfFfxo&#zx → † A2B2142C2132DEF32GHI: BooFxFofx3(-x)(-x)(-x)oo(-x)fff3xCofFoxof b3xoCxfAfxo&#zx → † A2B2142C2132DE12FGHI: BooFofofx3(-x)(-x)(-x)o(-x)offf3xCofAxxof b3xoCxFFfxo&#zx → † A2B2142C2132DE12FGHI1: BooFofof(-x)3(-x)(-x)(-x)o(-x)offF3xCofAxxof b3xoCxFFfxo&#zx → † A2B2142C2132DE12F32GHI: BooFoFofx3(-x)(-x)(-x)o(-x)(-x)fff3xCofAoxof b3xoCxFAfxo&#zx → † A2B2142C2132DE12F32GHI1: BooFoFof(-x)3(-x)(-x)(-x)o(-x)(-x)ffF3xCofAoxof b3xoCxFAfxo&#zx → † A2B2142C2132D42EFGHI: BooAxfofx3(-x)(-x)(-x)(-x)oofff3xCoFFxxof b3xoCofFfxo&#zx → † A2B2142C2132D42EF32GHI: BooAxFofx3(-x)(-x)(-x)(-x)o(-x)fff3xCoFFoxof b3xoCofAfxo&#zx → † A2B2142C2132D42E12FGHI: BooAofofx3(-x)(-x)(-x)(-x)(-x)offf3xCoFAxxof b3xoCoFFfxo&#zx → † A2B2142C2132D42E12FGHI1: BooAofof(-x)3(-x)(-x)(-x)(-x)(-x)offF3xCoFAxxof b3xoCoFFfxo&#zx → † A2B2142C2132D42E12F32GHI: BooAoFofx3(-x)(-x)(-x)(-x)(-x)(-x)fff3xCoFAoxof b3xoCoFAfxo&#zx → † A2B2142C2132D42E12F32GHI1: BooAoFof(-x)3(-x)(-x)(-x)(-x)(-x)(-x)ffF3xCoFAoxof b3xoCoFAfxo&#zx → † A23BC213DE1F3G3HI1: Bo(-x)F(-x)fof(-x)3oxxxoxFfF3(-x)V(-x)fF(-x)(-x)of b3xoBxfFfxo&#zx → † A23B2C2132DEF32G3HI: BxoFxFofx3o(-x)(-x)oo(-x)Fff3(-x)BofFo(-x)of b3xxCxfAfxo&#zx → † A23B2C2132DE12F32G3HI: BxoFoFofx3o(-x)(-x)o(-x)(-x)Fff3(-x)BofAo(-x)of b3xxCxFAfxo&#zx → † A23B2C2132D42EF32G3HI: BxoAxFofx3o(-x)(-x)(-x)o(-x)Fff3(-x)BoFFo(-x)of b3xxCofAfxo&#zx → † A23B2C2132D42E12F32G3HI: BxoAoFofx3o(-x)(-x)(-x)(-x)(-x)Fff3(-x)BoFAo(-x)of b3xxCoFAfxo&#zx → † A23B21C213DE1F3G3HI1: B(-x)(-x)F(-x)fof(-x)3ooxoxxFfF3(-x)B(-x)fF(-x)(-x)of b3xxBxfFfxo&#zx → † A23B21C2132DE12F32G3HI1: B(-x)oFoFof(-x)3oo(-x)o(-x)(-x)FfF3(-x)BofAo(-x)of b3xxCxFAfxo&#zx → † A23B21C2132D42E12F32G3HI1: B(-x)oAoFof(-x)3oo(-x)(-x)(-x)(-x)FfF3(-x)BoFAo(-x)of b3xxCoFAfxo&#zx → † A23B2142C2132DEF32G3HI: BooFxFofx3o(-x)(-x)oo(-x)Fff3(-x)CofFo(-x)of b3xoCxfAfxo&#zx → † A23B2142C2132DE12F32G3HI: BooFoFofx3o(-x)(-x)o(-x)(-x)Fff3(-x)CofAo(-x)of b3xoCxFAfxo&#zx → † A23B2142C2132DE12F32G3HI1: BooFoFof(-x)3o(-x)(-x)o(-x)(-x)FfF3(-x)CofAo(-x)of b3xoCxFAfxo&#zx → † A23B2142C2132D42EF32G3HI: BooAxFofx3o(-x)(-x)(-x)o(-x)Fff3(-x)CoFFo(-x)of b3xoCofAfxo&#zx → † A23B2142C2132D42E12F32G3HI: BooAoFofx3o(-x)(-x)(-x)(-x)(-x)Fff3(-x)CoFAo(-x)of b3xoCoFAfxo&#zx → † A23B2142C2132D42E12F32G3HI1: BooAoFof(-x)3o(-x)(-x)(-x)(-x)(-x)FfF3(-x)CoFAo(-x)of b3xoCoFAfxo&#zx → † A23B2142C23DEF32G3HI: BoxFxFofx3o(-x)ooo(-x)Fff3(-x)C(-x)fFo(-x)of b3xoBxfAfxo&#zx → † A23B2142C23DE12F32G3HI: BoxFoFofx3o(-x)oo(-x)(-x)Fff3(-x)C(-x)fAo(-x)of b3xoBxFAfxo&#zx → † A23B2142C23D42EF32G3HI: BoxAxFofx3o(-x)o(-x)o(-x)Fff3(-x)C(-x)FFo(-x)of b3xoBofAfxo&#zx → † A23B2142C23D42E12F32G3HI: BoxAoFofx3o(-x)o(-x)(-x)(-x)Fff3(-x)C(-x)FAo(-x)of b3xoBoFAfxo&#zx → † A234BC213D4E1F3G3H4I1: Bo(-x)F(-x)fof(-x)3xxxxxxFFF3(-x)V(-x)fF(-x)(-x)of b3(-x)oB(-x)fFf(-x)o&#zx → † A234B214CD4E1F3G3H4I1: B(-x)oF(-x)fof(-x)3xxxxxxFFF3(-x)BofF(-x)(-x)of b3(-x)(-x)V(-x)fFf(-x)o&#zx → † A234B214C213D4E1F3G3H4I1: B(-x)(-x)F(-x)fof(-x)3xxxxxxFFF3(-x)B(-x)fF(-x)(-x)of b3(-x)(-x)B(-x)fFf(-x)o&#zx → † A2342B2C2132DEFGHI: CxoFxfofx3(-x)(-x)(-x)ooofff3oBofFxxof b3oxCxfFfxo&#zx → † A2342B2C2132DEF32GHI: CxoFxFofx3(-x)(-x)(-x)oo(-x)fff3oBofFoxof b3oxCxfAfxo&#zx → † A2342B2C2132DEF32G3HI: CxoFxFofx3(-x)(-x)(-x)oo(-x)Fff3oBofFo(-x)of b3oxCxfAfxo&#zx → † A2342B2C2132DE12FGHI: CxoFofofx3(-x)(-x)(-x)o(-x)offf3oBofAxxof b3oxCxFFfxo&#zx → † A2342B2C2132DE12F32GHI: CxoFoFofx3(-x)(-x)(-x)o(-x)(-x)fff3oBofAoxof b3oxCxFAfxo&#zx → † A2342B2C2132DE12F32G3HI: CxoFoFofx3(-x)(-x)(-x)o(-x)(-x)Fff3oBofAo(-x)of b3oxCxFAfxo&#zx → † A2342B2C2132D42EFGHI: CxoAxfofx3(-x)(-x)(-x)(-x)oofff3oBoFFxxof b3oxCofFfxo&#zx → † A2342B2C2132D42EF32GHI: CxoAxFofx3(-x)(-x)(-x)(-x)o(-x)fff3oBoFFoxof b3oxCofAfxo&#zx → † A2342B2C2132D42EF32G3HI: CxoAxFofx3(-x)(-x)(-x)(-x)o(-x)Fff3oBoFFo(-x)of b3oxCofAfxo&#zx → † A2342B2C2132D42E12FGHI: CxoAofofx3(-x)(-x)(-x)(-x)(-x)offf3oBoFAxxof b3oxCoFFfxo&#zx → † A2342B2C2132D42E12F32GHI: CxoAoFofx3(-x)(-x)(-x)(-x)(-x)(-x)fff3oBoFAoxof b3oxCoFAfxo&#zx → † A2342B2C2132D42E12F32G3HI: CxoAoFofx3(-x)(-x)(-x)(-x)(-x)(-x)Fff3oBoFAo(-x)of b3oxCoFAfxo&#zx → † A2342B21C21DE12FGHI1: C(-x)(-x)Fofof(-x)3(-x)ooo(-x)offF3oBxfAxxof b3oxBxFFfxo&#zx → † A2342B21C21DE12F32GHI1: C(-x)(-x)FoFof(-x)3(-x)ooo(-x)(-x)ffF3oBxfAoxof b3oxBxFAfxo&#zx → † A2342B21C21D42E12FGHI1: C(-x)(-x)Aofof(-x)3(-x)oo(-x)(-x)offF3oBxFAxxof b3oxBoFFfxo&#zx → † A2342B21C21D42E12F32GHI1: C(-x)(-x)AoFof(-x)3(-x)oo(-x)(-x)(-x)ffF3oBxFAoxof b3oxBoFAfxo&#zx → † A2342B21C2132DE12FGHI1: C(-x)oFofof(-x)3(-x)o(-x)o(-x)offF3oBofAxxof b3oxCxFFfxo&#zx → † A2342B21C2132DE12F32GHI1: C(-x)oFoFof(-x)3(-x)o(-x)o(-x)(-x)ffF3oBofAoxof b3oxCxFAfxo&#zx → † A2342B21C2132DE12F32G3HI1: C(-x)oFoFof(-x)3(-x)o(-x)o(-x)(-x)FfF3oBofAo(-x)of b3oxCxFAfxo&#zx → † A2342B21C2132D42E12FGHI1: C(-x)oAofof(-x)3(-x)o(-x)(-x)(-x)offF3oBoFAxxof b3oxCoFFfxo&#zx → † A2342B21C2132D42E12F32GHI1: C(-x)oAoFof(-x)3(-x)o(-x)(-x)(-x)(-x)ffF3oBoFAoxof b3oxCoFAfxo&#zx → † A2342B21C2132D42E12F32G3HI1: C(-x)oAoFof(-x)3(-x)o(-x)(-x)(-x)(-x)FfF3oBoFAo(-x)of b3oxCoFAfxo&#zx → † A2342B2142C2DEFGHI: CoxFxfofx3(-x)(-x)(-x)ooofff3oCxfFxxof b3ooBxfFfxo&#zx → † A2342B2142C2DEF32GHI: CoxFxFofx3(-x)(-x)(-x)oo(-x)fff3oCxfFoxof b3ooBxfAfxo&#zx → † A2342B2142C2DE12FGHI: CoxFofofx3(-x)(-x)(-x)o(-x)offf3oCxfAxxof b3ooBxFFfxo&#zx → † A2342B2142C2DE12F32GHI: CoxFoFofx3(-x)(-x)(-x)o(-x)(-x)fff3oCxfAoxof b3ooBxFAfxo&#zx → † A2342B2142C2D42EFGHI: CoxAxfofx3(-x)(-x)(-x)(-x)oofff3oCxFFxxof b3ooBofFfxo&#zx → † A2342B2142C2D42EFGH4I: CoxAxfofx3(-x)(-x)(-x)(-x)oofFf3oCxFFxxof b3ooBofFf(-x)o&#zx → † A2342B2142C2D42EF32GHI: CoxAxFofx3(-x)(-x)(-x)(-x)o(-x)fff3oCxFFoxof b3ooBofAfxo&#zx → † A2342B2142C2D42EF32GH4I: CoxAxFofx3(-x)(-x)(-x)(-x)o(-x)fFf3oCxFFoxof b3ooBofAf(-x)o&#zx → † A2342B2142C2D42E12FGHI: CoxAofofx3(-x)(-x)(-x)(-x)(-x)offf3oCxFAxxof b3ooBoFFfxo&#zx → † A2342B2142C2D42E12FGH4I: CoxAofofx3(-x)(-x)(-x)(-x)(-x)ofFf3oCxFAxxof b3ooBoFFf(-x)o&#zx → † A2342B2142C2D42E12F32GHI: CoxAoFofx3(-x)(-x)(-x)(-x)(-x)(-x)fff3oCxFAoxof b3ooBoFAfxo&#zx → † A2342B2142C2D42E12F32GH4I: CoxAoFofx3(-x)(-x)(-x)(-x)(-x)(-x)fFf3oCxFAoxof b3ooBoFAf(-x)o&#zx → † A2342B2142C21DE12FGHI1: Co(-x)Fofof(-x)3(-x)(-x)oo(-x)offF3oCxfAxxof b3ooBxFFfxo&#zx → † A2342B2142C21DE12F32GHI1: Co(-x)FoFof(-x)3(-x)(-x)oo(-x)(-x)ffF3oCxfAoxof b3ooBxFAfxo&#zx → † A2342B2142C21D42E12FGHI1: Co(-x)Aofof(-x)3(-x)(-x)o(-x)(-x)offF3oCxFAxxof b3ooBoFFfxo&#zx → † A2342B2142C21D42E12FGH4I1: Co(-x)Aofof(-x)3(-x)(-x)o(-x)(-x)ofFF3oCxFAxxof b3ooBoFFf(-x)o&#zx → † A2342B2142C21D42E12F32GHI1: Co(-x)AoFof(-x)3(-x)(-x)o(-x)(-x)(-x)ffF3oCxFAoxof b3ooBoFAfxo&#zx → † A2342B2142C21D42E12F32GH4I1: Co(-x)AoFof(-x)3(-x)(-x)o(-x)(-x)(-x)fFF3oCxFAoxof b3ooBoFAf(-x)o&#zx → † A2342B2142C2132DEFGHI: CooFxfofx3(-x)(-x)(-x)ooofff3oCofFxxof b3ooCxfFfxo&#zx → † A2342B2142C2132DEF32GHI: CooFxFofx3(-x)(-x)(-x)oo(-x)fff3oCofFoxof b3ooCxfAfxo&#zx → † A2342B2142C2132DEF32G3HI: CooFxFofx3(-x)(-x)(-x)oo(-x)Fff3oCofFo(-x)of b3ooCxfAfxo&#zx → † A2342B2142C2132DE12FGHI: CooFofofx3(-x)(-x)(-x)o(-x)offf3oCofAxxof b3ooCxFFfxo&#zx → † A2342B2142C2132DE12FGHI1: CooFofof(-x)3(-x)(-x)(-x)o(-x)offF3oCofAxxof b3ooCxFFfxo&#zx → † A2342B2142C2132DE12F32GHI: CooFoFofx3(-x)(-x)(-x)o(-x)(-x)fff3oCofAoxof b3ooCxFAfxo&#zx → † A2342B2142C2132DE12F32GHI1: CooFoFof(-x)3(-x)(-x)(-x)o(-x)(-x)ffF3oCofAoxof b3ooCxFAfxo&#zx → † A2342B2142C2132DE12F32G3HI: CooFoFofx3(-x)(-x)(-x)o(-x)(-x)Fff3oCofAo(-x)of b3ooCxFAfxo&#zx → † A2342B2142C2132DE12F32G3HI1: CooFoFof(-x)3(-x)(-x)(-x)o(-x)(-x)FfF3oCofAo(-x)of b3ooCxFAfxo&#zx → † A2342B2142C2132D42EFGHI: CooAxfofx3(-x)(-x)(-x)(-x)oofff3oCoFFxxof b3ooCofFfxo&#zx → † A2342B2142C2132D42EFGH4I: CooAxfofx3(-x)(-x)(-x)(-x)oofFf3oCoFFxxof b3ooCofFf(-x)o&#zx → † A2342B2142C2132D42EF32GHI: CooAxFofx3(-x)(-x)(-x)(-x)o(-x)fff3oCoFFoxof b3ooCofAfxo&#zx → † A2342B2142C2132D42EF32GH4I: CooAxFofx3(-x)(-x)(-x)(-x)o(-x)fFf3oCoFFoxof b3ooCofAf(-x)o&#zx → † A2342B2142C2132D42EF32G3HI: CooAxFofx3(-x)(-x)(-x)(-x)o(-x)Fff3oCoFFo(-x)of b3ooCofAfxo&#zx → † A2342B2142C2132D42EF32G3H4I: CooAxFofx3(-x)(-x)(-x)(-x)o(-x)FFf3oCoFFo(-x)of b3ooCofAf(-x)o&#zx → † A2342B2142C2132D42E12FGHI: CooAofofx3(-x)(-x)(-x)(-x)(-x)offf3oCoFAxxof b3ooCoFFfxo&#zx → † A2342B2142C2132D42E12FGHI1: CooAofof(-x)3(-x)(-x)(-x)(-x)(-x)offF3oCoFAxxof b3ooCoFFfxo&#zx → † A2342B2142C2132D42E12FGH4I: CooAofofx3(-x)(-x)(-x)(-x)(-x)ofFf3oCoFAxxof b3ooCoFFf(-x)o&#zx → † A2342B2142C2132D42E12FGH4I1: CooAofof(-x)3(-x)(-x)(-x)(-x)(-x)ofFF3oCoFAxxof b3ooCoFFf(-x)o&#zx → † A2342B2142C2132D42E12F32GHI: CooAoFofx3(-x)(-x)(-x)(-x)(-x)(-x)fff3oCoFAoxof b3ooCoFAfxo&#zx → † A2342B2142C2132D42E12F32GHI1: CooAoFof(-x)3(-x)(-x)(-x)(-x)(-x)(-x)ffF3oCoFAoxof b3ooCoFAfxo&#zx → † A2342B2142C2132D42E12F32GH4I: CooAoFofx3(-x)(-x)(-x)(-x)(-x)(-x)fFf3oCoFAoxof b3ooCoFAf(-x)o&#zx → † A2342B2142C2132D42E12F32GH4I1: CooAoFof(-x)3(-x)(-x)(-x)(-x)(-x)(-x)fFF3oCoFAoxof b3ooCoFAf(-x)o&#zx → † A2342B2142C2132D42E12F32G3HI: CooAoFofx3(-x)(-x)(-x)(-x)(-x)(-x)Fff3oCoFAo(-x)of b3ooCoFAfxo&#zx → † A2342B2142C2132D42E12F32G3HI1: CooAoFof(-x)3(-x)(-x)(-x)(-x)(-x)(-x)FfF3oCoFAo(-x)of b3ooCoFAfxo&#zx → † A2342B2142C2132D42E12F32G3H4I: CooAoFofx3(-x)(-x)(-x)(-x)(-x)(-x)FFf3oCoFAo(-x)of b3ooCoFAf(-x)o&#zx → † A2342B2142C2132D42E12F32G3H4I1: CooAoFof(-x)3(-x)(-x)(-x)(-x)(-x)(-x)FFF3oCoFAo(-x)of b3ooCoFAf(-x)o&#zx → † A2342B2142C23DEF32G3HI: CoxFxFofx3(-x)(-x)ooo(-x)Fff3oC(-x)fFo(-x)of b3ooBxfAfxo&#zx → † A2342B2142C23DE12F32G3HI: CoxFoFofx3(-x)(-x)oo(-x)(-x)Fff3oC(-x)fAo(-x)of b3ooBxFAfxo&#zx → † A2342B2142C23D42EF32G3HI: CoxAxFofx3(-x)(-x)o(-x)o(-x)Fff3oC(-x)FFo(-x)of b3ooBofAfxo&#zx → † A2342B2142C23D42EF32G3H4I: CoxAxFofx3(-x)(-x)o(-x)o(-x)FFf3oC(-x)FFo(-x)of b3ooBofAf(-x)o&#zx → † A2342B2142C23D42E12F32G3HI: CoxAoFofx3(-x)(-x)o(-x)(-x)(-x)Fff3oC(-x)FAo(-x)of b3ooBoFAfxo&#zx → † A2342B2142C23D42E12F32G3H4I: CoxAoFofx3(-x)(-x)o(-x)(-x)(-x)FFf3oC(-x)FAo(-x)of b3ooBoFAf(-x)o&#zx → † A2342B24C2132D42EFGH4I: CxoAxfofx3(-x)o(-x)(-x)oofFf3oBoFFxxof b3o(-x)CofFf(-x)o&#zx → † A2342B24C2132D42EF32GH4I: CxoAxFofx3(-x)o(-x)(-x)o(-x)fFf3oBoFFoxof b3o(-x)CofAf(-x)o&#zx → † A2342B24C2132D42EF32G3H4I: CxoAxFofx3(-x)o(-x)(-x)o(-x)FFf3oBoFFo(-x)of b3o(-x)CofAf(-x)o&#zx → † A2342B24C2132D42E12FGH4I: CxoAofofx3(-x)o(-x)(-x)(-x)ofFf3oBoFAxxof b3o(-x)CoFFf(-x)o&#zx → † A2342B24C2132D42E12F32GH4I: CxoAoFofx3(-x)o(-x)(-x)(-x)(-x)fFf3oBoFAoxof b3o(-x)CoFAf(-x)o&#zx → † A2342B24C2132D42E12F32G3H4I: CxoAoFofx3(-x)o(-x)(-x)(-x)(-x)FFf3oBoFAo(-x)of b3o(-x)CoFAf(-x)o&#zx → † A24B214CD4E1FGH4I1: B(-x)oF(-x)fof(-x)3oxxxxofFF3xBofFxxof b3(-x)(-x)V(-x)fFf(-x)o&#zx → † A24B214C21D4E1FGH4I1: B(-x)(-x)F(-x)fof(-x)3oxoxxofFF3xBxfFxxof b3(-x)(-x)B(-x)fFf(-x)o&#zx → † A24B2142C2D42EFGH4I: BoxAxfofx3o(-x)(-x)(-x)oofFf3xCxFFxxof b3(-x)oBofFf(-x)o&#zx → † A24B2142C2D42EF32GH4I: BoxAxFofx3o(-x)(-x)(-x)o(-x)fFf3xCxFFoxof b3(-x)oBofAf(-x)o&#zx → † A24B2142C2D42E12FGH4I: BoxAofofx3o(-x)(-x)(-x)(-x)ofFf3xCxFAxxof b3(-x)oBoFFf(-x)o&#zx → † A24B2142C2D42E12F32GH4I: BoxAoFofx3o(-x)(-x)(-x)(-x)(-x)fFf3xCxFAoxof b3(-x)oBoFAf(-x)o&#zx → † A24B2142C21D42E12FGH4I1: Bo(-x)Aofof(-x)3o(-x)o(-x)(-x)ofFF3xCxFAxxof b3(-x)oBoFFf(-x)o&#zx → † A24B2142C21D42E12F32GH4I1: Bo(-x)AoFof(-x)3o(-x)o(-x)(-x)(-x)fFF3xCxFAoxof b3(-x)oBoFAf(-x)o&#zx → † A24B2142C2132D42EFGH4I: BooAxfofx3o(-x)(-x)(-x)oofFf3xCoFFxxof b3(-x)oCofFf(-x)o&#zx → † A24B2142C2132D42EF32GH4I: BooAxFofx3o(-x)(-x)(-x)o(-x)fFf3xCoFFoxof b3(-x)oCofAf(-x)o&#zx → † A24B2142C2132D42E12FGH4I: BooAofofx3o(-x)(-x)(-x)(-x)ofFf3xCoFAxxof b3(-x)oCoFFf(-x)o&#zx → † A24B2142C2132D42E12FGH4I1: BooAofof(-x)3o(-x)(-x)(-x)(-x)ofFF3xCoFAxxof b3(-x)oCoFFf(-x)o&#zx → † A24B2142C2132D42E12F32GH4I: BooAoFofx3o(-x)(-x)(-x)(-x)(-x)fFf3xCoFAoxof b3(-x)oCoFAf(-x)o&#zx → † A24B2142C2132D42E12F32GH4I1: BooAoFof(-x)3o(-x)(-x)(-x)(-x)(-x)fFF3xCoFAoxof b3(-x)oCoFAf(-x)o&#zx → †
Stott expansion: (derived CRFs)	2:A2B2C2DEFGHI: Bxx\|Fxf\|ofx 3 ooo\|xxx\|FFF 3 xBx\|fFx\|xof *b3 xxB\|xfF\|fxo &#zx → CRF with cell list: 24 coes 24 ikes 192 oct 144 pip 288 squippies (J1) 96 thawroes (J92) 96 tricues (J3) 96 trip
using here node marks / (pseudo) edge lengths: `F=f+x=ff, V=F+v=2f, A=F+x=f+2x, B=V+x=2f+x=fff, C=2F=2f+2x, R=A+x=f+3x, S=C+x=2f+3x`

in `o5o2o5o` subsymmetry (up)
Representation:	Aooo\|Fxox\|Vofo\|Fofx\|xf 5 oAoo\|xFxo\|oVof\|oFxf\|xf 2 ooAo\|xoFx\|ofVo\|xfFo\|fx 5 oooA\|oxxF\|fooV\|fxoF\|fx &#zx (rox) with cyclical layer symmetries: A(1234) → B(2143) → C(4312) → D(3421) → A(1234) E(1234) → F(2143) → G(4312) → H(3421) → E(1234) I(1234) → J(2143) → K(4312) → L(3421) → I(1234) M(1234) → N(2143) → O(4312) → P(3421) → M(1234) Q(1234) → Q(2143) → R(4312) → R(3421) → Q(1234)
All layers & kaleido-facetings per layer:	A: A5o o5o B: o5A o5o C: o5o A5o D: o5o o5A E: F5x x5o → E2: B5(-x) x5o → E23: B5(-x) (-x)5f ↳ E3: F5x (-x)5f F: x5F o5x → F1: (-x)5B o5x → F14: (-x)5B f5(-x) ↳ F4: x5F f5(-x) G: o5x F5x → G2: f5(-x) F5x → G24: f5(-x) B5(-x) ↳ G4: o5x B5(-x) H: x5o x5F → H1: (-x)5f x5F → H13: (-x)5f (-x)5B ↳ H3: x5o (-x)5B	I: V5o o5f J: o5V f5o K: f5o V5o L: o5f o5V M: F5o x5f → M3: F5o (-x)5V N: o5F f5x → N4: o5F V5(-x) O: f5x F5o → O2: V5(-x) F5o P: x5f o5F → P1: (-x)5V o5F Q: x5x f5f → Q1: (-x)5F f5f ↳ Q2: F5(-x) f5f R: f5f x5x → R3: f5f (-x)5F ↳ R4: f5f F5(-x)
A priori invalid combinations:	E + G2,G24,H3,H13,M3,O2,Q2,R3 E2 + G,G4,H3,H13,M3,O,Q,R3 E3 + G2,G24,H,H1,M,O2,Q2,R E23 + G,G4,H,H1,M,O,Q,R F + G4,G24,H1,H13,N4,P1,Q1,R4 F1 + G4,G24,H,H3,N4,P,Q,R4 F4 + G,G2,H1,H13,N,P1,Q1,R F14 + G,G2,H,H3,N,P,Q,R G + N4,O2,Q2,R4 G2 + N4,O,Q,R4 G4 + N,O2,Q2,R G24 + N,O,Q,R	H + M3,P1,Q1,R3 H1 + M3,P,Q,R3 H3 + M,P1,Q1,R H13 + M,P,Q,R M + R3 M3 + R N + R4 N4 + R O + Q2 O2 + Q P + Q1 P1 + Q
Other layer-combinations:	E2F1G2H1MNO2P1Q1R: AoooB(-x)f(-x)VofoFoV(-x)(-x)f 5 oAoo(-x)B(-x)foVofoF(-x)VFf 2 ooAoxoFxofVoxfFofx 5 oooAoxxFfooVfxoFfx &#zx E23F14G24H13M3N4O2P1Q1R3: AoooB(-x)f(-x)VofoFoV(-x)(-x)f 5 oAoo(-x)B(-x)foVofoF(-x)VFf 2 ooAo(-x)fB(-x)ofVo(-x)VFof(-x) 5 oooAf(-x)(-x)BfooVV(-x)oFfF &#zx
Stott expansion: (derived potential CRFs)	12:E2F1G2H1MNO2P1Q1R: RxxxCoFoBxFxAxBooF 5 xRxxoCoFxBxFxAoBAF 2 ooAoxoFxofVoxfFofx 5 oooAoxxFfooVfxoFfx &#zx → ‡ (F in G)
Stott expansion: (derived potential CRFs)	1234:E23F14G24H13M3N4O2P1Q1R3: RxxxCoFoBxFxAxBooF 5 xRxxoCoFxBxFxAoBAF 2 xxRxoFCoxFBxoBAxFo 5 xxxRFooCFxxBBoxAFA &#zx → ‡ (F in G)
using here node marks / (pseudo) edge lengths: `F=f+x=ff, V=F+v=2f, A=F+x=f+2x, B=V+x=2f+x=fff, C=2F=2f+2x, R=A+x=f+3x`

in `o3o2o3o` subsymmetry (up)
Representation:	oxoxofxfoFfoVxFfFxVoBoBFfAxBFVoCfB 3 xoxofofxFofVoFxFfVxBoBoFAfBxVFCoBf 2 fBCoVFBxfAFBooBVxfFFxoVfFoxfofoxxo 3 BfoCFVxBAfFoBBoxVFfxFVofoFfxfoxoox &#zx (rox) with cyclical layer symmetries: A(1234) → a(3421) → B(2143) → b(4312) → A(1234) C(1234) → d(3421) → D(2143) → c(4312) → D(1234) E(1234) → f(3421) → F(2143) → e(4312) → E(1234) G(1234) → h(3421) → H(2143) → g(4312) → G(1234) I(1234) → i(3421) → J(2143) → j(4312) → I(1234) K(1234) → k(3421) → K(2143) L(1234) → m(3421) → M(2143) → l(4312) → L(1234) N(1234) → n(3421) → O(2143) → o(4312) → N(1234) P(1234) → q(3421) → Q(2143) → p(4312) → P(1234)
All layers & kaleido-facetings per layer:	A: o3x f3B → A2: x 3(-x) f 3 B → A21: (-x)3 o f 3 B B: x3o B3f → B1: (-x)3 x B 3 f → B12: o 3(-x) B 3 f C: o3x C3o → C2: x 3(-x) C 3 o → C21: (-x)3 o C 3 o D: x3o o3C → D1: (-x)3 x o 3 C → D12: o 3(-x) o 3 C E: o3f V3F F: f3o F3V G: x3f B3x → G1: (-x)3 F B 3 x → G14: (-x)3 F C 3(-x) ↳ G4: x 3 f C 3(-x) H: f3x x3B → H2: F 3(-x) x 3 B → H23: F 3(-x)(-x)3 C ↳ H3: f 3 x (-x)3 C I: o3F f3A J: F3o A3f K: f3f F3F L: o3V B3o M: V3o o3B N: x3F o3B → N1: (-x)3 A o 3 B O: F3x B3o → O2: A 3(-x) B 3 o P: f3F V3x → P4: f 3 F B 3(-x) Q: F3f x3V → Q3: F 3 f (-x)3 B	q: x3V f3F → q1: (-x)3 B f 3 F p: V3x F3f → p2: B 3(-x) F 3 f o: o3B F3x → o4: o 3 B A 3(-x) n: B3o x3F → n3: B 3 o (-x)3 A m: o3B o3V l: B3o V3o k: F3F f3f j: f3A F3o i: A3f o3F h: x3B x3f → h1: (-x)3 C x 3 f → h13: (-x)3 C (-x)3 F ↳ h3: x 3 B (-x)3 F g: B3x f3x → g2: C 3(-x) f 3 x → g24: C 3(-x) F 3(-x) ↳ g4: B 3 x F 3(-x) f: F3V o3f e: V3F f3o d: o3C o3x → d4: o 3 C x 3(-x) → d43: o 3 C (-x)3 o c: C3o x3o → c3: C 3 o (-x)3 x → c34: C 3 o o 3(-x) b: f3B x3o → b3: f 3 B (-x)3 x → b34: f 3 B o 3(-x) a: B3f o3x → a4: B 3 f x 3(-x) → a43: B 3 f (-x)3 o
A priori invalid combinations:	none of A2, B, C2, D, G, G4, N, q, h, h3 shall combine with any of A21, B1, C21, D1, G1, G14, N1, q1, h1, h13 (else asking for u edges finally) none of A, B1, C, D1, H, H3, O, p, g, g4 shall combine with any of A2, B12, C2, D12, H2, H23, O2, p2, g2, g24 (else asking for u edges finally) none of H, H2, Q, n, h, h1, d4, c, b, a4 shall combine with any of H23, H3, Q3, n3, h13, h3, d43, c3, b3, a43 (else asking for u edges finally) none of G, G1, P, o, g, g2, d, c3, b3, a shall combine with any of G14, G4, P4, o4, g24, g4, d4, c34, b34, a4 (else asking for u edges finally)
Other layer-combinations:	A2C2H2O2p2g2: xxxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)o(-x)ofof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFBxfAFBooBVxfFFxoVfFoxfofoxxo 3 BfoCFVxBAfFoBBoxVFfxFVofoFfxfoxoox A2B12C2H2O2p2g2: xoxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)ofof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFBxfAFBooBVxfFFxoVfFoxfofoxxo 3 BfoCFVxBAfFoBBoxVFfxFVofoFfxfoxoox A2C2D12H2O2p2g2: xxxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)o(-x)(-x)fof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFBxfAFBooBVxfFFxoVfFoxfofoxxo 3 BfoCFVxBAfFoBBoxVFfxFVofoFfxfoxoox A2B12C2D12H2O2p2g2: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)(-x)fof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFBxfAFBooBVxfFFxoVfFoxfofoxxo 3 BfoCFVxBAfFoBBoxVFfxFVofoFfxfoxoox A2C2G4H2O2P4p2o4g24d4a4: xxxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)o(-x)ofof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxxxx 3 BfoCFV(-x)BAfFoBBo(-x)VFf(-x)FVofoFf(-x)fo(-x)oo(-x) A2B12C2G4H2O2P4p2o4g24d4a4: xoxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)ofof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxxxx 3 BfoCFV(-x)BAfFoBBo(-x)VFf(-x)FVofoFf(-x)fo(-x)oo(-x) A2B12C2H23O2Q3p2n3h3g2c3b3: xoxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)ofof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFB(-x)fAFBooBV(-x)fFF(-x)oVfFo(-x)fofo(-x)(-x)o 3 BfoCFVxCAfFoBBoxBFfxAVofoFFxfoxxxx A2C2D12G4H2O2P4p2o4g24d4a4: xxxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)o(-x)(-x)fof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxxxx 3 BfoCFV(-x)BAfFoBBo(-x)VFf(-x)FVofoFf(-x)fo(-x)oo(-x) A2C2D12H23O2Q3p2n3h3g2c3b3: xxxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)o(-x)(-x)fof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFB(-x)fAFBooBV(-x)fFF(-x)oVfFo(-x)fofo(-x)(-x)o 3 BfoCFVxCAfFoBBoxBFfxAVofoFFxfoxxxx A21B12C21D12G1H2N1O2q1p2h1g2: (-x)o(-x)oof(-x)FoFfoV(-x)AfF(-x)BoBoBFfA(-x)CFVoCfB 3 o(-x)o(-x)foF(-x)FofVoA(-x)FfB(-x)BoBoFAfC(-x)VFCoBf 2 fBCoVFBxfAFBooBVxfFFxoVfFoxfofoxxo 3 BfoCFVxBAfFoBBoxVFfxFVofoFfxfoxoox A2B12C2D12G4H2O2P4p2o4g24d4a4: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)(-x)fof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxxxx 3 BfoCFV(-x)BAfFoBBo(-x)VFf(-x)FVofoFf(-x)fo(-x)oo(-x) A2B12C2D12H23O2Q3p2n3h3g2c3b3: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)(-x)fof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFB(-x)fAFBooBV(-x)fFF(-x)oVfFo(-x)fofo(-x)(-x)o 3 BfoCFVxCAfFoBBoxBFfxAVofoFFxfoxxxx A2B12C2G4H2O2P4p2o4g24d4b34a4: xoxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)ofof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxxox 3 BfoCFV(-x)BAfFoBBo(-x)VFf(-x)FVofoFf(-x)fo(-x)o(-x)(-x) A2B12C2G4H2O2P4p2o4g24d4c34a4: xoxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)ofof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxoxx 3 BfoCFV(-x)BAfFoBBo(-x)VFf(-x)FVofoFf(-x)fo(-x)(-x)o(-x) A2B12C2H23O2Q3p2n3h3g2d43c3b3: xoxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)ofof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFB(-x)fAFBooBV(-x)fFF(-x)oVfFo(-x)fof(-x)(-x)(-x)o 3 BfoCFVxCAfFoBBoxBFfxAVofoFFxfooxxx A2C2D12G4H2O2P4p2o4g24d4c34a4: xxxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)o(-x)(-x)fof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxoxx 3 BfoCFV(-x)BAfFoBBo(-x)VFf(-x)FVofoFf(-x)fo(-x)(-x)o(-x) A2B12C2D12G4H2O2P4p2o4g24d4b34a4: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)(-x)fof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxxox 3 BfoCFV(-x)BAfFoBBo(-x)VFf(-x)FVofoFf(-x)fo(-x)o(-x)(-x) A2B12C2D12G4H2O2P4p2o4g24d4c34a4: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)(-x)fof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxoxx 3 BfoCFV(-x)BAfFoBBo(-x)VFf(-x)FVofoFf(-x)fo(-x)(-x)o(-x) A2B12C2D12H23O2Q3p2n3h3g2c3b3a43: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)(-x)fof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFB(-x)fAFBooBV(-x)fFF(-x)oVfFo(-x)fofo(-x)(-x)(-x) 3 BfoCFVxCAfFoBBoxBFfxAVofoFFxfoxxxo A2B12C2D12H23O2Q3p2n3h3g2d43c3b3: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)(-x)fof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFB(-x)fAFBooBV(-x)fFF(-x)oVfFo(-x)fof(-x)(-x)(-x)o 3 BfoCFVxCAfFoBBoxBFfxAVofoFFxfooxxx A2B12C2D12G4H2O2P4p2o4g24d4c34b34a4: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)(-x)fof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxoox 3 BfoCFV(-x)BAfFoBBo(-x)VFf(-x)FVofoFf(-x)fo(-x)(-x)(-x)(-x) A2C2G4H23O2P4Q3p2o4n3h3g24d43c34b34a43: xxxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)o(-x)ofof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFC(-x)fAFBooBB(-x)fFA(-x)oVfFo(-x)Fof(-x)oo(-x) 3 BfoCFV(-x)CAfFoBBo(-x)BFf(-x)AVofoFF(-x)foo(-x)(-x)o A2B12C2G4H23O2P4Q3p2o4n3h3g24d43c34b34a43: xoxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)ofof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFC(-x)fAFBooBB(-x)fFA(-x)oVfFo(-x)Fof(-x)oo(-x) 3 BfoCFV(-x)CAfFoBBo(-x)BFf(-x)AVofoFF(-x)foo(-x)(-x)o A2C2D12G4H23O2P4Q3p2o4n3h3g24d43c34b34a43: xxxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)o(-x)(-x)fof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFC(-x)fAFBooBB(-x)fFA(-x)oVfFo(-x)Fof(-x)oo(-x) 3 BfoCFV(-x)CAfFoBBo(-x)BFf(-x)AVofoFF(-x)foo(-x)(-x)o A2B12C2D12G4H23O2P4Q3p2o4n3h3g24d43c34b34a43: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 (-x)(-x)(-x)(-x)fof(-x)FofVoF(-x)FfV(-x)BoBoFAfB(-x)VFCoBf 2 fBCoVFC(-x)fAFBooBB(-x)fFA(-x)oVfFo(-x)Fof(-x)oo(-x) 3 BfoCFV(-x)CAfFoBBo(-x)BFf(-x)AVofoFF(-x)foo(-x)(-x)o A21B12C21D12G14H23N1O2P4Q3q1p2o4n3h13g24d43c34b34a43: (-x)o(-x)oof(-x)FoFfoV(-x)AfF(-x)BoBoBFfA(-x)CFVoCfB 3 o(-x)o(-x)foF(-x)FofVoA(-x)FfB(-x)BoBoFAfC(-x)VFCoBf 2 fBCoVFC(-x)fAFBooBB(-x)fFA(-x)oVfFo(-x)Fof(-x)oo(-x) 3 BfoCFV(-x)CAfFoBBo(-x)BFf(-x)AVofoFF(-x)foo(-x)(-x)o
Stott expansion: (derived CRFs)	2:A2C2H2O2p2g2: xxxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 oxoxFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 fBCoVFBxfAFBooBVxfFFxoVfFoxfofoxxo 3 BfoCFVxBAfFoBBoxVFfxFVofoFfxfoxoox &#zx → ‡ (eg. \|DF\|=\|FI\|=q and \|DI\|=f)
	2:A2B12C2H2O2p2g2: xoxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 oooxFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 fBCoVFBxfAFBooBVxfFFxoVfFoxfofoxxo 3 BfoCFVxBAfFoBBoxVFfxFVofoFfxfoxoox &#zx → ‡ (eg. \|DF\|=\|FI\|=q and \|DI\|=f)
	2:A2C2D12H2O2p2g2: xxxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 oxooFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 fBCoVFBxfAFBooBVxfFFxoVfFoxfofoxxo 3 BfoCFVxBAfFoBBoxVFfxFVofoFfxfoxoox &#zx → ‡ (eg. \|FI\|=q)
	2:A2B12C2D12H2O2p2g2: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 ooooFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 fBCoVFBxfAFBooBVxfFFxoVfFoxfofoxxo 3 BfoCFVxBAfFoBBoxVFfxFVofoFfxfoxoox &#zx → ‡ (eg. \|FI\|=q)
	24:A2C2G4H2O2P4p2o4g24d4a4: xxxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 oxoxFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxxxx 3 CFxSABoCRFAxCCxoBAFoABxFxAFoFxoxxo &#zx → ‡ (eg. \|BB\|=F)
	24:A2C2G4H2O2P4p2o4g24d4a4: xoxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 oooxFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxxxx 3 CFxSABoCRFAxCCxoBAFoABxFxAFoFxoxxo &#zx → ‡ (eg. \|BB\|=F)
	23:A2B12C2H23O2Q3p2n3h3g2c3b3: xoxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 oooxFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 FCSxBACoFRACxxCBoFAAoxBFAxoFxFxoox 3 BfoCFVxCAfFoBBoxBFfxAVofoFFxfoxxxx &#zx → †
	24:A2C2D12G4H2O2P4p2o4g24d4a4: xxxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 oxooFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxxxx 3 CFxSABoCRFAxCCxoBAFoABxFxAFoFxoxxo &#zx → ‡ (eg. \|II\|=f)
	23:A2C2D12H23O2Q3p2n3h3g2c3b3: xxxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 oxooFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 FCSxBACoFRACxxCBoFAAoxBFAxoFxFxoox 3 BfoCFVxCAfFoBBoxBFfxAVofoFFxfoxxxx &#zx → ‡ (eg. \|AA\|=F)
	12:A21B12C21D12G1H2N1O2q1p2h1g2: oxoxxFoAxAFxBoRFAoCxCxCAFRoSABxSFC 3 xoxoFxAoAxFBxRoAFCoCxCxARFSoBASxCF 2 fBCoVFBxfAFBooBVxfFFxoVfFoxfofoxxo 3 BfoCFVxBAfFoBBoxVFfxFVofoFfxfoxoox &#zx → †
	24:A2B12C2D12G4H2O2P4p2o4g24d4a4: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 ooooFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxxxx 3 CFxSABoCRFAxCCxoBAFoABxFxAFoFxoxxo &#zx → †
	23:A2B12C2D12H23O2Q3p2n3h3g2c3b3: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 ooooFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 FCSxBACoFRACxxCBoFAAoxBFAxoFxFxoox 3 BfoCFVxCAfFoBBoxBFfxAVofoFFxfoxxxx &#zx → †
	24:A2B12C2G4H2O2P4p2o4g24d4b34a4: xoxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 oooxFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxxox 3 CFxSABoCRFAxCCxoBAFoABxFxAFoFxoxoo &#zx → †
	24:A2B12C2G4H2O2P4p2o4g24d4c34a4: xoxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 oooxFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxoxx 3 CFxSABoCRFAxCCxoBAFoABxFxAFoFxooxo &#zx → †
	23:A2B12C2H23O2Q3p2n3h3g2d43c3b3: xoxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 oooxFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 FCSxBACoFRACxxCBoFAAoxBFAxoFxFooox 3 BfoCFVxCAfFoBBoxBFfxAVofoFFxfooxxx &#zx → †
	24:A2C2D12G4H2O2P4p2o4g24d4c34a4 xxxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 oxooFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxoxx 3 CFxSABoCRFAxCCxoBAFoABxFxAFoFxooxo &#zx → ‡ (eg. \|BB\|=F)
	24:A2B12C2D12G4H2O2P4p2o4g24d4b34a4: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 ooooFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxxox 3 CFxSABoCRFAxCCxoBAFoABxFxAFoFxoxoo &#zx → †
	24:A2B12C2D12G4H2O2P4p2o4g24d4c34a4: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 ooooFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxoxx 3 CFxSABoCRFAxCCxoBAFoABxFxAFoFxooxo &#zx → †
	23:A2B12C2D12H23O2Q3p2n3h3g2c3b3a43: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 ooooFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 FCSxBACoFRACxxCBoFAAoxBFAxoFxFxooo 3 BfoCFVxCAfFoBBoxBFfxAVofoFFxfoxxxo &#zx → †
	23:A2B12C2D12H23O2Q3p2n3h3g2d43c3b3: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 ooooFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 FCSxBACoFRACxxCBoFAAoxBFAxoFxFooox 3 BfoCFVxCAfFoBBoxBFfxAVofoFFxfooxxx &#zx → †
	24:A2B12C2D12G4H2O2P4p2o4g24d4c34b34a4: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 ooooFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 fBCoVFCxfAFBooBBxfFAxoVfFoxFofxoox 3 CFxSABoCRFAxCCxoBAFoABxFxAFoFxoooo &#zx → †
	234:A2C2G4H23O2P4Q3p2o4n3h3g24d43c34b34a43: xxxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 oxoxFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 FCSxBASoFRACxxCCoFARoxBFAxoAxFoxxo 3 CFxSABoSRFAxCCxoCAFoRBxFxAAoFxxoox &#zx → ‡ (eg. \|ae\|=\|bf\|=f)
	234:A2B12C2G4H23O2P4Q3p2o4n3h3g24d43c34b34a43: xoxxofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 oooxFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 FCSxBASoFRACxxCCoFARoxBFAxoAxFoxxo 3 CFxSABoSRFAxCCxoCAFoRBxFxAAoFxxoox &#zx → ‡ (eg. \|ae\|=\|bf\|=f)
	234:A2C2D12G4H23O2P4Q3p2o4n3h3g24d43c34b34a43: xxxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 oxooFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 FCSxBASoFRACxxCCoFARoxBFAxoAxFoxxo 3 CFxSABoSRFAxCCxoCAFoRBxFxAAoFxxoox &#zx → ‡ (eg. \|ae\|=\|bf\|=f)
	234:A2B12C2D12G4H23O2P4Q3p2o4n3h3g24d43c34b34a43: xoxoofxFoFfoVxAfFxBoBoBFfAxCFVoCfB 3 ooooFxFoAxFBxAoAFBoCxCxARFCoBASxCF 2 FCSxBASoFRACxxCCoFARoxBFAxoAxFoxxo 3 CFxSABoSRFAxCCxoCAFoRBxFxAAoFxxoox &#zx → ‡ (eg. \|ae\|=\|bf\|=f)
	1234:A21B12C21D12G14H23N1O2P4Q3q1p2o4n3h13g24d43c34b34a43: oxoxxFoAxAFxBoRFAoCxCxCAFRoSABxSFC 3 xoxoFxAoAxFBxRoAFCoCxCxARFSoBASxCF 2 FCSxBASoFRACxxCCoFARoxBFAxoAxFoxxo 3 CFxSABoSRFAxCCxoCAFoRBxFxAAoFxxoox &#zx → †
using here node marks / (pseudo) edge lengths: `F=f+x=ff, V=F+v=2f, A=F+x=f+2x, B=V+x=2f+x=fff, C=B+x=2F=2f+2x, R=A+x=f+3x, S=C+x=2f+3x`

EKF of the small prismated icositetrachoron (`x3o4o3x`)

©

in `o2o3o4o` subsymmetry (up)
Representation:	oxqwQ 2 qowxx 3 xxooo 4 oxoxo &#zx (spic)
All layers & kaleido-facetings per layer:	A: o2q3x4o → A3: o2w3(-x)4q B: x2o3x4x → B1: (-x)2o3x4x → B13: (-x)2x3(-x)4w → B132: (-x)2(-x)3o4w ↳ B14: (-x)2o3w4(-x) ↳ B3: x2x3(-x)4w → (B31 = B13) ↳ B32: x2(-x)3o4w → (B321 = B132) ↳ B4: x2o3w4(-x) → (B41 = B14) C: q2w3o4o D: w2x3o4x → D2: w2(-x)3x4x → D23: w2o3(-x)4w ↳ D24: w2(-x)3w4(-x) ↳ D4: w2x3q4(-x) → (D42 = D24) E: Q2x3o4o → E2: Q2(-x)3x4o → E23: Q2o3(-x)4q
A priori invalid combinations:	A + B3,B13,D23,E23 A3 + B,B1,D2,E2 B + D4,D23,D24,E23 B1 + D4,D23,D24,E23 B3 + D2,D24,E2 B4 + D,D2 B13 + D2,D24,E2 B14 + D,D2 B32 + D,D4,E B132 + D,D4,E D + E2 D2 + E,E23 D4 + E2 D23 + E2 D24 + E (all giving rise to u edges) E23 (giving rise to q or w edges within extremal layer)
Other layer-combinations:	ABCD2E2 oxqwQ 2 qow(-x)(-x) 3 xxoxx 4 oxoxo &#zx → ‡ (dead end at C) AB1CDE o(-x)qwQ 2 qowxx 3 xxooo 4 oxoxo &#zx → ‡ (q in A) AB1CD2E2 o(-x)qwQ 2 qow(-x)(-x) 3 xxoxx 4 oxoxo &#zx → † AB4CD4E oxqwQ 2 qowxx 3 xwoqo 4 o(-x)o(-x)o &#zx → ‡ (q in A) AB4CD24E2 oxqwQ 2 qow(-x)(-x) 3 xwowx 4 o(-x)o(-x)o &#zx → ‡ (dead end at C) AB14CD4E o(-x)qwQ 2 qowxx 3 xwoqo 4 o(-x)o(-x)o &#zx → ‡ (w in B) AB14CD24E2 o(-x)qwQ 2 qow(-x)(-x) 3 xwowx 4 o(-x)o(-x)o &#zx → † AB32CD2E2 oxqwQ 2 q(-x)w(-x)(-x) 3 xooxx 4 owoxo &#zx → † AB32CD24E2 oxqwQ 2 q(-x)w(-x)(-x) 3 xoowx 4 owo(-x)o &#zx → † AB132CD24E2 o(-x)qwQ 2 q(-x)w(-x)(-x) 3 xoowx 4 owo(-x)o &#zx → † A3B3CDE oxqwQ 2 wxwxx 3 (-x)(-x)ooo 4 qwoxo &#zx A3B3CD4E oxqwQ 2 wxwxx 3 (-x)(-x)oqo 4 qwo(-x)o &#zx → ‡ (dead end at B) A3B3CD23E oxqwQ 2 wxwox 3 (-x)(-x)o(-x)o 4 qwowo &#zx → † A3B4CD4E oxqwQ 2 wowxx 3 (-x)woqo 4 q(-x)o(-x)o &#zx → ‡ (w in C) A3B4CD23E oxqwQ 2 wowox 3 (-x)wo(-x)o 4 q(-x)owo &#zx → † A3B13CDE o(-x)qwQ 2 wxwxx 3 (-x)(-x)ooo 4 qwoxo &#zx → ‡ (w in C) A3B13CD4E o(-x)qwQ 2 wxwxx 3 (-x)(-x)oqo 4 qwo(-x)o &#zx → ‡ (w in D) A3B13CD23E o(-x)qwQ 2 wxwox 3 (-x)(-x)o(-x)o 4 qwowo &#zx → † A3B14CD4E o(-x)qwQ 2 wowxx 3 (-x)woqo 4 q(-x)o(-x)o &#zx → † A3B14CD23E o(-x)qwQ 2 wowox 3 (-x)wo(-x)o 4 q(-x)owo &#zx → †
Stott expansion: (derived CRFs)	3:A3B3CDE: oxqwQ 2 wxwxx 3 ooxxx 4 qwoxo &#zx → CRF with cell list: 6 coes 16 hips 12 sircoes 12 squobcues (J28) 2 toes 16 tricues (J3) 80 trips related: oxqw. 2 wxwx. 3 ooxx. 4 qwox. &#zx → CRF with cell list: 6 coes 2 gircoes 12 sircoes 12 squacues (J4) 16 tricues (J3) 56 trips
using here node marks / (pseudo) edge lengths: `Q=w+x=q+u, W=Q+x=w+u`
in `. o3o4o` subsymmetry (up)
additional, not prismatically symmetric combinations of formers:	none

in `o3o3o *b3o` subsymmetry (up)
Representation:	qoo 3 xxx 3 oqo *b3ooq &#zx (spic) with layer cycle: A(134) → B(341) → C(413) → A(134)
All layers & kaleido-facetings per layer:	A: q3x3o b3o → A2: w3(-x)3x b3x → A23: w3o3(-x) b3x → A234: w3x3(-x) b3(-x) → A2342: Q3(-x)3o b3o ↳ A24: w3o3x b3(-x) → (A243 = A234) → (A2432 = A2342) B: o3x3q b3o → B2: x3(-x)3w b3x → B21: (-x)3o3w b3x → B214: (-x)3x3w b3(-x) → B2142: o3(-x)3Q b3o ↳ B24: x3o3w b3(-x) → (B241 = B214) → (B2412 = B2142) C: o3x3o b3q → C2: x3(-x)3x b3w → C21: (-x)3o3x b3w → C213: (-x)3x3(-x) b3w → C2132: o3(-x)3o b3Q ↳ C23: x3o3(-x) b3w → (C231 = C213) → (C2312 = C2132)
A priori invalid combinations:	A + B2,B2142,C2,C2132 A2 + B,B24,B214,C,C23,C213 A23 + B24,B214,C2,C21 A24 + B21,C2,C23,C213 A234 + B2,B21,B2142,C2,C21,C2132 A2342 + B,B214,C,C213	B + C2,C213 B2 + C,C21,C213 B21 + C2,C23 B24 + C21,C213 B214 + C2,C23,C2132 B2142 + C,C213
Other layer-combinations:	ABC21 qo(-x) 3 xxo 3 oqx b3 oow &#zx → † ABC23 qox 3 xxo 3 oq(-x) b3 oow &#zx → † AB21C21 q(-x)(-x) 3 xoo 3 owx b3 oxw &#zx → † AB21C213 q(-x)(-x) 3 xox 3 ow(-x) b3 oxw &#zx → † AB24C23 qxx 3 xoo 3 ow(-x) b3 o(-x)w &#zx → † AB214C21 q(-x)(-x) 3 xxo 3 owx b3 o(-x)w &#zx → † AB214C213 q(-x)(-x) 3 xxx 3 ow(-x) b3 o(-x)w &#zx → † A2B2C2 wxx 3 (-x)(-x)(-x) 3 xwx b3 xxw &#zx A2B2C2132 wxo 3 (-x)(-x)(-x) 3 xwo b3 xxQ &#zx → † A2B21C21 w(-x)(-x) 3 (-x)oo 3 xwx b3 xxw &#zx → † A2B21C2132 w(-x)o 3 (-x)o(-x) 3 xwo b3 xxQ &#zx → † A2B2142C21 wo(-x) 3 (-x)(-x)o 3 xQx b3 xow &#zx → † A2B2142C2132 woo 3 ( -x)(-x)(-x) 3 xQo b3 xoQ &#zx → † A23B21C213 w(-x)(-x) 3 oox 3 (-x)w(-x) b3 xxw &#zx → † A23B21C2132 w(-x)o 3 oo(-x) 3 (-x)wo b3 xxQ &#zx → † A23B2142C23 wox 3 o(-x)o 3 (-x)Q(-x) b3 xow &#zx → † A23B2142C2132 woo 3 o(-x)(-x) 3 (-x)Qo b3 xoQ &#zx → † A24B2142C2132 woo 3 o(-x)(-x) 3 xQo b3 (-x)oQ &#zx → † A234B214C213 w(-x)(-x) 3 xxx 3 (-x)w(-x) b3 (-x)(-x)w &#zx → † A2342B2142C2132 Qoo 3 (-x)(-x)(-x) 3 oQo b3 ooQ &#zx → †
Stott expansion: (derived CRFs)	1:ABC wxx 3 xxx 3 oqo b3 ooq &#zx (owauprit) → CRF with cell list: 24 esquidpies (J15) 32 hips 8 octs 160 trips 16 tuts related: .xx 3 .xx 3 .qo b3 .oq &#zx = Wythoffian x3x3o4x (prit) with cell list: 24 cubes 32 hips 8 sircoes 16 tuts	(-2):ABC qoo 3 ooo 3 oqo b3 ooq &#zx = Wythoffian x3o4o3o (ico) with cell list: 24 octs related: .oo 3 .oo 3 .qo b3 .oq &#zx = Wythoffian o3o3o4x (tes) with cell list: 8 cubes
	1(-2):ABC wxx 3 ooo 3 oqo b3 ooq &#zx (poxic) → CRF with cell list: 24 esquidpies (J15) 16 tets 32 trips related: .xx 3 .oo 3 .qo b3 .oq &#zx = Wythoffian x3o3o4x (sidpith) with cell list: 32 cubes 16 tets 32 trips	13:ABC wxx 3 xxx 3 xwx b3 ooq &#zx (poc prico) → CRF with cell list: 64 hips 24 squobcues (J28) 8 toes 128 trips 16 tuts related: wx. 3 xx. 3 xw. b3 oo. &#zx = Wythoffian o3x3x4x (grit) with cell list: 8 gircoes 32 trips 16 tuts
	1(-2)3:ABC wxx 3 ooo 3 xwx b3 ooq &#zx (pocsric) → CRF with cell list: 8 coes 24 squobcues (J28) 16 tets 64 trips related: wx. 3 oo. 3 xw. b3 oo. &#zx = Wythoffian x3o3x4x (tat) with cell list: 16 tets 8 tics	134:ABC wxx 3 xxx 3 xwx b3 xxw &#zx = Wythoffian x3x4o3x (prico) with cell list: 96 hips 24 sircoes 24 toes 96 trips related: .xx 3 .xx 3 .wx b3 .xw &#zx = Wythoffian x3x3x4x (gidpith) with cell list: 8 gircoes 32 hips 24 ops 16 toes
	1(-2)34:ABC wxx 3 ooo 3 xwx b3 xxw &#zx = Wythoffian x3o4x3o (srico) with cell list: 24 coes 24 sircoes 6 trips related: wx. 3 oo. 3 xw. b3 xx. &#zx = Wythoffian x3o3x4x (proh) with cell list: 16 coes 24 ops 8 tics 32 trips	2:A2B2C2 wxx 3 ooo 3 xwx b3 xxw &#zx = Wythoffian x3o4x3o (srico) with cell list: 24 coes 24 sircoes 6 trips related: wx. 3 oo. 3 xw. b3 xx. &#zx = Wythoffian x3o3x4x (proh) with cell list: 16 coes 24 ops 8 tics 32 trips
	(-1)2:A2B2C2 qoo 3 ooo 3 xwx b3 xxw &#zx (pocsric) → CRF with cell list: 8 coes 24 squobcues (J28) 16 tets 64 trips related: .oo 3 .oo 3 .wx b3 .xw &#zx = Wythoffian x3o3x4x (tat) with cell list: 16 tets 8 tics	(-1)2(-3):A2B2C2 qoo 3 ooo 3 oqo b3 xxw &#zx (poxic) → CRF with cell list: 24 esquidpies (J15) 16 tets 32 trips related: qo. 3 oo. 3 oq. b3 xx. &#zx = Wythoffian x3o3o4x (sidpith) with cell list: 32 cubes 16 tets 32 trips
	(-1)2(-3)(-4):A2B2C2 qoo 3 ooo 3 oqo b3 ooq &#zx = Wythoffian x3o4o3o (ico) with cell list: 24 octs related: .oo 3 .oo 3 .qo b3 .oq &#zx = Wythoffian o3o3o4x (tes) with cell list: 8 cubes
using here node marks / (pseudo) edge lengths: `Q=w+x=q+u, W=Q+x=w+u`

EKF of the snub (dis)icositetrachoron (`s3s4o3o`)

©

in `o3o3o *b3o` subsymmetry (up)
Representation:	fox 3 ooo 3 xfo *b3 oxf &#zx (sadi) with layer cycle: A(1234) → B(3241) → C(4213) → A(1234)
All layers & kaleido-facetings per layer:	A: f3o3x b3o → A3: f3x3(-x) b3o → A32: F3(-x)3o b3x → A324: F3o3o b3(-x) B: o3o3f b3x → B4: o3x3f b3(-x) → B42: x3(-x)3F b3o → B421: (-x)3o3F b3o C: x3o3o b3f → C1: (-x)3x3o b3f → C12: o3(-x)3x b3F → C123: o3o3(-x) b3F
A priori invalid combinations:	A + C123 A3 + B42,C12 A32 + B4,C1 A324 + B B4 + C12 B42 + C1 B421 + C (all giving rise to u edges)
Other layer-combinations:	ABC1 fo(-x)3oox3xfo b3oxf&#zx ABC12 foo3oo(-x)3xfx b3oxF&#zx → ‡ (f in A) AB4C1 fo(-x)3oxx3xfo b3o(-x)f&#zx → † AB42C12 fxo3o(-x)(-x)3xFx b3ooF&#zx → † AB421C1 f(-x)(-x)3oox3xFo b3oof&#zx → † AB421C12 f(-x)o3oo(-x)3xFx b3ooF&#zx → † A3B4C1 fo(-x)3xxx3(-x)fo b3o(-x)f&#zx → † A3B4C123 foo3xxo3(-x)f(-x) b3o(-x)F&#zx → † A3B421C123 f(-x)o3xoo3(-x)F(-x) b3ooF&#zx → † A32B42C12 Fxo3(-x)(-x)(-x)3oFx b3xoF&#zx → † A32B42C123 Fxo3(-x)(-x)o3oF(-x) b3xoF&#zx → † A32B421C123 F(-x)o3(-x)oo3oF(-x) b3xoF&#zx → † A324B421C123 F(-x)o3ooo3oF(-x) *b3(-x)oF&#zx → †
Stott expansion: (derived CRFs)	1:ABC1: Fxo 3 oox 3 xfo *b3 oxf &#zx (pretasto) → CRF with cell list: 24 bilbiroes (J91) 8 coes 40 octs 32 teddies (J63) 40 tets	2:ABC: fox 3 xxx 3 xfo *b3 oxf &#zx (prissi) → CRF with cell list: 24 ikes 96 tricues (J3) 96 trips 24 tuts
using here node marks / (pseudo) edge lengths: `F=f+x`

in `o2o2o2o` subsymmetry (up)
Representation:	ooo\|xxx\|fff\|FFF 2 Fxf\|oFf\|xFo\|fxo 2 xfF\|Ffo\|Fox\|xof 2 fFx\|foF\|oxF\|ofx &#zx (sadi) with layer cycles: (ABCDEFGHIJKL)(1234) → (KFHAJIELBGDC)(3124) → (ILDGBKCFJAHE)(2431) → (BCAEFDHIGKLJ)(1423) → (JEGCLHDKAIFB)(4132) → (GJEHCLADKBIF)(4321) → (ABCDEFGHIJKL)(4321)
All layers & kaleido-facetings per layer:	A: o2F2x2f → A3: o2F2(-x)2f B: o2x2f2F → B2: o2(-x)2f2F C: o2f2F2x → C4: o2f2F2(-x) D: x2o2F2f → D1: (-x)2o2F2f E: x2F2f2o → E1: (-x)2F2f2o F: x2f2o2F → F1: (-x)2f2o2F G: f2x2F2o → G2: f2(-x)2F2o H: f2F2o2x → H4: f2F2o2(-x) I: f2o2x2F → I3: f2o2(-x)2F J: F2f2x2o → J3: F2f2(-x)2o K: F2x2o2f → K2: F2(-x)2o2f L: F2o2f2x → L4: F2o2f2(-x)
A priori invalid combinations:	A + I3,J3 A3 + I,J B + G2,K2 B2 + G,K C + H4,L4 C4 + H,L D + E1,F1 D1 + E,F	E + F1 E1 + F G + K2 G2 + K H + L4 H4 + L I + J3 I3 + J (all giving rise to u edges)
Other layer-combinations:	ABCD1E1F1GHIJKL ooo(-x)(-x)(-x)fffFFF 2 FxfoFfxFofxo 2 xfFFfoFoxxof 2 fFxfoFoxFofx &#zx ABC4D1E1F1GH4IJKL4 ooo(-x)(-x)(-x)fffFFF 2 FxfoFfxFofxo 2 xfFFfoFoxxof 2 fF(-x)foFo(-x)Fof(-x) &#zx → ‡ (extremal f-edge DG) AB2C4D1E1F1G2H4IJK2L4 ooo(-x)(-x)(-x)fffFFF 2 F(-x)foFf(-x)Fof(-x)o 2 xfFFfoFoxxof 2 fF(-x)foFo(-x)Fof(-x) &#zx → † A3B2C4D1E1F1G2H4I3J3K2L4 ooo(-x)(-x)(-x)fffFFF 2 F(-x)foFf(-x)Fof(-x)o 2 (-x)fFFfoFo(-x)(-x)of 2 fF(-x)foFo(-x)Fof(-x) &#zx → †
Stott expansion: (derived CRFs)	1:ABCD1E1F1GHIJKL: xxxoooFFFAAA 2 FxfoFfxFofxo 2 xfFFfoFoxxof 2 fFxfoFoxFofx &#zx → CRF with cell list: 6 bilbiroes (J91) 2 ikes 36 squippies (J1) 40 teddies (J63) 36 tets 8 trips
using here node marks / (pseudo) edge lengths: `F=f+x, A=f+u=f+2x`

EKF of the rectified tesseract (`o3o3x4o`)

©

in `o2o3o4o` subsymmetry (up)
Representation:	qo 2 oo 3 xo 4 oq &#zx (rit)
All layers & kaleido-facetings per layer:	A: q2o3x4o → A3: q2x3(-x)4q B: o2o3o4q
A priori invalid combinations:	neither can A+A3 be applied on either side (providing extremal u-edges) (which thus excludes any mere . o3o4o symmetry) nor can A3 be applied without an additional applied partial q-contraction in the last node (else providing extremal q-edges) even when using A only, then node 1 and node 4 still has to correspond, in order not to produce non-regular hexagons (i.e. diagonally elongated squares) there
Stott expansion: (derived potential CRFs)	2:AB qo 2 xx 3 xo 4 oq &#zx (pabdirico) → CRF with cell list: 6 coes 12 cubes 2 toes 16 tricues (J3)	14:AB wx 2 oo 3 xo 4 xw &#zx = Wythoffian o3o3x4x (tat) with cell list: 16 tets 8 tics
	124:AB wx 2 xx 3 xo 4 xw &#zx (pabdiproh) → CRF with cell list: 2 gircoes 12 ops 6 tics 16 tricues (J3) 8 trips	3(-q4):A3B qo 2 xo 3 ox 4 oo &#zx = Wythoffian x3o4o3o (ico) with cell list: 24 octs
	13(-q4):A3B wx 2 xo 3 ox 4 oo &#zx (pexic) → CRF with cell list: 6 esquidpies (J15) 18 octs 8 trips	34(-q4):A3B qo 2 xo 3 ox 4 xx &#zx (pacsrit) → CRF with cell list: 16 octs 2 sircoes 6 squobcues (J28) 24 trips
	134(-q4):A3B wx 2 xo 3 ox 4 xx &#zx = Wythoffian `o3x3o4x` (srit) with cell list: 16 octs 8 sircoes 32 trips

in `. o3o3o` subsymmetry (up)
Representation:	ooxx 3 oxxo 3 xxoo &#xt (rit) with inversive top-down-symmetry
All layers & kaleido-facetings per layer:	A: o3o3x → A3: o3x3(-x) → A32: x3(-x)3o → A321 (-x)3o3o B: o3x3x → B2: x3(-x)3u → B21: (-x)3o3u ↳ B3: o3u3(-x) C: x3x3o → C1: (-x)3u3o ↳ C2: u3(-x)3x → C23: u3o3(-x) D: x3o3o → D1: (-x)3x3o → D12: o3(-x)3x → D123: o3o3(-x)
A priori invalid combinations:	A + B3,C23,D123 A3 + B,B2,B21,C2,D12 A32 + B,B21,B3,C,C1,D1 A321 + B2,C,C2,C23,D B + C2,C23,D12,D123 B2 + C,C1,C23,D1,D123 B21 + C,C2,C23,D,D123 B3 + C2,D12 C + D1,D12 C1 + D,D12 C2 + D1,D123 C23 + D1,D12,D123
Other layer-combinations:	ABC1D1 oo(-x)(-x) 3 oxux 3 xxoo &#xt AB2C2D oxux 3 o(-x)(-x)o 3 xuxo &#xt AB2C2D12 oxuo 3 o(-x)(-x)(-x) 3 xuxx &#xt → † AB21C1D1 o(-x)(-x)(-x) 3 ooux 3 xuoo &#xt → † A3B3CD123 ooxo 3 xuxo 3 (-x)(-x)o(-x) &#xt → † A3B3C1D1 oo(-x)(-x) 3 xuux 3 (-x)(-x)oo &#xt A3B3C1D123 oo(-x)o 3 xuuo 3 (-x)(-x)o(-x) &#xt → † A32B2C2D12 xxuo 3 (-x)(-x)(-x)(-x) 3 ouxx &#xt → † A321B3C1D123 (-x)o(-x)o 3 ouuo 3 o(-x)o(-x) &#xt → †
Stott expansion: (derived potential CRFs)	1:ABC1D1 xxoo 3 oxux 3 xxoo &#xt → CRF with cell list: 1 co 6 cubes 1 oct 6 squippies (J1) 8 tricues (J3) 8 tuts related: xx.. 3 ox.. 3 xx.. &#x (coatoe) → CRF (segmentochoron) with cell list: 1 co 6 cubes 8 tricues (J3) 1 toe related: .xoo 3 .xux 3 .xoo &#xt (octum) → CRF with cell list: 1 oct 6 squippies (J1) 1 toe 8 tuts	2:AB2C2D oxux 3 xoox 3 xuxo &#xt = Wythoffian x3x3o4o (thex) with cell list: 8 octs 16 tuts
Stott expansion: (derived potential CRFs)	1(-2)3:A3B3C1D1 xxoo 3 oxxo 3 ooxx &#xt = Wythoffian o3o3x4o (rit) with cell list: 8 coes 16 tets related: xx.. 3 ox.. 3 oo.. &#x (tetatut) → CRF (segmentochoron) with cell list: 5 tets 4 tricues (J3) 1 tut related: .xo. 3 .xx. 3 .ox. &#x (tuta) → CRF (segmentochoron) with cell list: 6 tets 8 tricues (J3) 2 tuts

top of page

in `o3o3o *b3o` subsymmetry (up)
Representation:	qoo 3 ooo 3 oqo *b3 ooq &#zx (ico)
All layers & kaleido-facetings per layer:	A: q3o3o b3o B: o3o3q b3o C: o3o3o *b3q (As this representation does not show up (true / x-) edges within the layers, those thus cannot be inverted either. Therefore at most pure partial Stott expansions wrt. this subsymmetry remain possible.)
Stott expansion: (derived potential CRFs)	1:-: wxx 3 ooo 3 oqo b3 ooq &#zx (poxic) → CRF with cell list: 24 esquidpies (J15) 16 tets 32 trips related: .xx 3 .oo 3 .qo b3 .oq &#zx = Wythoffian x3o3o4x (sidpith) with cell list: 32 cubes 16 tets 32 trips	2:-: qoo 3 xxx 3 oqo b3 ooq &#zx = Wythoffian `x3o4o3x` (spic) with cell list: 48 octs 192 trips related: .oo 3 .xx 3 .qo b3 .oq &#zx = Wythoffian o3x3o4x (srit) with cell list: 16 octs 8 sircoes 32 trips
	12:-: wxx 3 xxx 3 oqo b3 ooq &#zx (owau prit) → CRF with cell list: 24 esquidpies (J15) 32 hips 8 octs 160 trips 16 tuts related: .xx 3 .xx 3 .qo b3 .oq &#zx = Wythoffian x3x3o4x (prit) with cell list: 24 cubes 32 hips 8 sircoes 16 tuts	13:-: wxx 3 ooo 3 xwx b3 ooq &#zx (pocsric) → CRF with cell list: 8 coes 24 squobcues (J28) 16 tets 64 trips related: wx. 3 oo. 3 xw. b3 oo. &#zx = Wythoffian x3o3x4x (tat) with cell list: 16 tets 8 tics
	123:-: wxx 3 xxx 3 xwx b3 ooq &#zx (poc prico) → CRF with cell list: 64 hips 24 squobcues (J28) 8 toes 128 trips 16 tuts related: wx. 3 xx. 3 xw. b3 oo. &#zx = Wythoffian o3x3x4x (grit) with cell list: 8 gircoes 32 trips 16 tuts	134:-: wxx 3 ooo 3 xwx b3 xxw &#zx = Wythoffian `x3o4x3o` (srico) with cell list: 24 coes 24 sircoes 96 trips related: wx. 3 oo. 3 xw. b3 xx. &#zx = Wythoffian x3o3x4x (proh) with cell list: 16 coes 24 ops 8 tics 32 trips
	1234:-: wxx 3 xxx 3 xwx b3 xxw &#zx = Wythoffian `x3x4o3x` (prico) with cell list: 96 hips 24 sircoes 24 toes 96 trips related: .xx 3 .xx 3 .wx b3 .xw &#zx = Wythoffian x3x3x4x (gidpith) with cell list: 8 gircoes 32 hips 24 ops 16 toes

in `o3o3o *b3o` subsymmetry (up)
Representation:	qoo 3 xxx 3 oqo *b3ooq &#zx (spic) with layer cycle: A(134) → B(341) → C(413) → A(134)
All layers & kaleido-facetings per layer:	A: q3x3o b3o → A2: w3(-x)3x b3x → A23: w3o3(-x) b3x → A234: w3x3(-x) b3(-x) → A2342: Q3(-x)3o b3o ↳ A24: w3o3x b3(-x) → (A243 = A234) → (A2432 = A2342) B: o3x3q b3o → B2: x3(-x)3w b3x → B21: (-x)3o3w b3x → B214: (-x)3x3w b3(-x) → B2142: o3(-x)3Q b3o ↳ B24: x3o3w b3(-x) → (B241 = B214) → (B2412 = B2142) C: o3x3o b3q → C2: x3(-x)3x b3w → C21: (-x)3o3x b3w → C213: (-x)3x3(-x) b3w → C2132: o3(-x)3o b3Q ↳ C23: x3o3(-x) b3w → (C231 = C213) → (C2312 = C2132)
A priori invalid combinations:	A + B2,B2142,C2,C2132 A2 + B,B24,B214,C,C23,C213 A23 + B24,B214,C2,C21 A24 + B21,C2,C23,C213 A234 + B2,B21,B2142,C2,C21,C2132 A2342 + B,B214,C,C213	B + C2,C213 B2 + C,C21,C213 B21 + C2,C23 B24 + C21,C213 B214 + C2,C23,C2132 B2142 + C,C213
Other layer-combinations:	ABC21 qo(-x) 3 xxo 3 oqx b3 oow &#zx → † ABC23 qox 3 xxo 3 oq(-x) b3 oow &#zx → † AB21C21 q(-x)(-x) 3 xoo 3 owx b3 oxw &#zx → † AB21C213 q(-x)(-x) 3 xox 3 ow(-x) b3 oxw &#zx → † AB24C23 qxx 3 xoo 3 ow(-x) b3 o(-x)w &#zx → † AB214C21 q(-x)(-x) 3 xxo 3 owx b3 o(-x)w &#zx → † AB214C213 q(-x)(-x) 3 xxx 3 ow(-x) b3 o(-x)w &#zx → † A2B2C2 wxx 3 (-x)(-x)(-x) 3 xwx b3 xxw &#zx A2B2C2132 wxo 3 (-x)(-x)(-x) 3 xwo b3 xxQ &#zx → † A2B21C21 w(-x)(-x) 3 (-x)oo 3 xwx b3 xxw &#zx → † A2B21C2132 w(-x)o 3 (-x)o(-x) 3 xwo b3 xxQ &#zx → † A2B2142C21 wo(-x) 3 (-x)(-x)o 3 xQx b3 xow &#zx → † A2B2142C2132 woo 3 ( -x)(-x)(-x) 3 xQo b3 xoQ &#zx → † A23B21C213 w(-x)(-x) 3 oox 3 (-x)w(-x) b3 xxw &#zx → † A23B21C2132 w(-x)o 3 oo(-x) 3 (-x)wo b3 xxQ &#zx → † A23B2142C23 wox 3 o(-x)o 3 (-x)Q(-x) b3 xow &#zx → † A23B2142C2132 woo 3 o(-x)(-x) 3 (-x)Qo b3 xoQ &#zx → † A24B2142C2132 woo 3 o(-x)(-x) 3 xQo b3 (-x)oQ &#zx → † A234B214C213 w(-x)(-x) 3 xxx 3 (-x)w(-x) b3 (-x)(-x)w &#zx → † A2342B2142C2132 Qoo 3 (-x)(-x)(-x) 3 oQo b3 ooQ &#zx → †
Stott expansion: (derived CRFs)	1:ABC wxx 3 xxx 3 oqo b3 ooq &#zx (owauprit) → CRF with cell list: 24 esquidpies (J15) 32 hips 8 octs 160 trips 16 tuts related: .xx 3 .xx 3 .qo b3 .oq &#zx = Wythoffian x3x3o4x (prit) with cell list: 24 cubes 32 hips 8 sircoes 16 tuts	(-2):ABC qoo 3 ooo 3 oqo b3 ooq &#zx = Wythoffian x3o4o3o (ico) with cell list: 24 octs related: .oo 3 .oo 3 .qo b3 .oq &#zx = Wythoffian o3o3o4x (tes) with cell list: 8 cubes
	1(-2):ABC wxx 3 ooo 3 oqo b3 ooq &#zx (poxic) → CRF with cell list: 24 esquidpies (J15) 16 tets 32 trips related: .xx 3 .oo 3 .qo b3 .oq &#zx = Wythoffian x3o3o4x (sidpith) with cell list: 32 cubes 16 tets 32 trips	13:ABC wxx 3 xxx 3 xwx b3 ooq &#zx (poc prico) → CRF with cell list: 64 hips 24 squobcues (J28) 8 toes 128 trips 16 tuts related: wx. 3 xx. 3 xw. b3 oo. &#zx = Wythoffian o3x3x4x (grit) with cell list: 8 gircoes 32 trips 16 tuts
	1(-2)3:ABC wxx 3 ooo 3 xwx b3 ooq &#zx (pocsric) → CRF with cell list: 8 coes 24 squobcues (J28) 16 tets 64 trips related: wx. 3 oo. 3 xw. b3 oo. &#zx = Wythoffian x3o3x4x (tat) with cell list: 16 tets 8 tics	134:ABC wxx 3 xxx 3 xwx b3 xxw &#zx = Wythoffian x3x4o3x (prico) with cell list: 96 hips 24 sircoes 24 toes 96 trips related: .xx 3 .xx 3 .wx b3 .xw &#zx = Wythoffian x3x3x4x (gidpith) with cell list: 8 gircoes 32 hips 24 ops 16 toes
	1(-2)34:ABC wxx 3 ooo 3 xwx b3 xxw &#zx = Wythoffian x3o4x3o (srico) with cell list: 24 coes 24 sircoes 6 trips related: wx. 3 oo. 3 xw. b3 xx. &#zx = Wythoffian x3o3x4x (proh) with cell list: 16 coes 24 ops 8 tics 32 trips	2:A2B2C2 wxx 3 ooo 3 xwx b3 xxw &#zx = Wythoffian x3o4x3o (srico) with cell list: 24 coes 24 sircoes 6 trips related: wx. 3 oo. 3 xw. b3 xx. &#zx = Wythoffian x3o3x4x (proh) with cell list: 16 coes 24 ops 8 tics 32 trips
	(-1)2:A2B2C2 qoo 3 ooo 3 xwx b3 xxw &#zx (pocsric) → CRF with cell list: 8 coes 24 squobcues (J28) 16 tets 64 trips related: .oo 3 .oo 3 .wx b3 .xw &#zx = Wythoffian x3o3x4x (tat) with cell list: 16 tets 8 tics	(-1)2(-3):A2B2C2 qoo 3 ooo 3 oqo b3 xxw &#zx (poxic) → CRF with cell list: 24 esquidpies (J15) 16 tets 32 trips related: qo. 3 oo. 3 oq. b3 xx. &#zx = Wythoffian x3o3o4x (sidpith) with cell list: 32 cubes 16 tets 32 trips
	(-1)2(-3)(-4):A2B2C2 qoo 3 ooo 3 oqo b3 ooq &#zx = Wythoffian x3o4o3o (ico) with cell list: 24 octs related: .oo 3 .oo 3 .qo b3 .oq &#zx = Wythoffian o3o3o4x (tes) with cell list: 8 cubes
using here node marks / (pseudo) edge lengths: `Q=w+x=q+u, W=Q+x=w+u`