Acronym	thawro, J92
Name	triangular hebesphenorotunda
	© ©   ©   ©
Vertex figure	[(3,5)2], [3,4,3,5], [33,5], [32,4,6]
General of army	(is itself convex)
Colonel of regiment	(is itself locally convex)
Dihedral angles	between {3} and {4} (lunaic):   arccos(-(1+sqrt(5))/sqrt(12)) = 159.094843° between {3} and {5} (rotundal):   arccos(-sqrt[(5+2 sqrt(5))/15]) = 142.622632° between {3} and {3}:   arccos(-sqrt(5)/3) = 138.189685° between {3} and {6}:   arccos(-sqrt(5)/3) = 138.189685° between {4} and {6}:   arccos(-sqrt[(3-sqrt(5))/6]) = 110.905157° between {3} and {4} (across rim):   arccos(-sqrt[(3-sqrt(5))/6]) = 110.905157° between {3} and {5} (across rim):   arccos(-sqrt[(5-2 sqrt(5))/15]) = 100.812317°
Face vector	18, 36, 20
Confer	uniform relative: ike   id   srid   related Johnson solids: pocuro   bilbiro   general polytopal classes: Johnson solids   expanded kaleido-facetings
External links

At the first view this polyhedron looks odd, a real find. But consider the base hexagon being scaled by τ = (1+sqrt(5))/2, keeping its orientation and remaining coplanar. The lacing edges incident to that hexagon thereby all keep their lengths. Thus that figure would then be described by xfof3oxFf&#xt. The f-hexagon incident faces then are golden x-x-f triangles, respectively x-x-x-f trapeziae. Both are complementary parts of regular pentagons. And in fact, this derived figure is nothing but a triangle face parallel rotunda (i.e. half) of the id.

This polyhedron is related not only to id (that 3 pentagons plus 4 triangles patch) but also to srid (the 3 lunes out of a square and 2 attached triangles each).

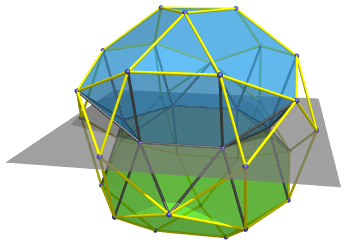
The right pic shows however how thawro can be obtained directly by means of an expanded kaleido-faceting from ike. And this relation too is why thawro occures not too seldomly as a cell within CRFs.

As abstract polytope thawro is isomorphic to githawro, thereby replacing pentagons by pentagrams.

It might be pointed out that twice the diheral angle between the squares and the hexagon happens to be just the complement of the dihedral angle between the hexagons of a ti. This nice coincidence gives rise to quite a pleasing toroid, built from nothing but just 20 thawroes (as if being placed on top of an afterwards again removed ti), thereby blending out those adjoining squares: oxFx3xfox5fovo&#zxt.

Incidence matrix according to Dynkin symbol

xfox3oxFx&#xt   → height(1,2) = height(3,4) = 1/sqrt(3) = 0.577350
(F=ff=x+f)        height(2,3) = sqrt[(3-sqrt(5))/6] = 0.356822
({3} || pseudo (f,x)-{6} || pseudo dual F-{3} || {6})

o...3o...     | 3 * * * | 2 2 0 0 0 0 0 0 | 1 2 1 0 0 0 0  [(3,5)2]
.o..3.o..     | * 6 * * | 0 1 1 1 1 0 0 0 | 0 1 1 1 1 0 0  [3,4,3,5]
..o.3..o.     | * * 3 * | 0 0 0 2 0 2 0 0 | 0 1 0 0 2 1 0  [33,5]
...o3...o     | * * * 6 | 0 0 0 0 1 1 1 1 | 0 0 0 1 1 1 1  [32,4,6]
--------------+---------+-----------------+--------------
x... ....     | 2 0 0 0 | 3 * * * * * * * | 1 1 0 0 0 0 0
oo..3oo..&#x  | 1 1 0 0 | * 6 * * * * * * | 0 1 1 0 0 0 0
.... .x..     | 0 2 0 0 | * * 3 * * * * * | 0 0 1 1 0 0 0
.oo.3.oo.&#x  | 0 1 1 0 | * * * 6 * * * * | 0 1 0 0 1 0 0
.o.o3.o.o&#x  | 0 1 0 1 | * * * * 6 * * * | 0 0 0 1 1 0 0
..oo3..oo&#x  | 0 0 1 1 | * * * * * 6 * * | 0 0 0 0 1 1 0
...x ....     | 0 0 0 2 | * * * * * * 3 * | 0 0 0 0 0 1 1
.... ...x     | 0 0 0 2 | * * * * * * * 3 | 0 0 0 1 0 0 1
--------------+---------+-----------------+--------------
x...3o...     | 3 0 0 0 | 3 0 0 0 0 0 0 0 | 1 * * * * * *
xfo. ....&#xt | 2 2 1 0 | 1 2 0 2 0 0 0 0 | * 3 * * * * *  {5}
.... ox..&#x  | 1 2 0 0 | 0 2 1 0 0 0 0 0 | * * 3 * * * *
.... .x.x&#x  | 0 2 0 2 | 0 0 1 0 2 0 0 1 | * * * 3 * * *  {4}
.ooo3.ooo&#xt | 0 1 1 1 | 0 0 0 1 1 1 0 0 | * * * * 6 * *
..ox ....&#x  | 0 0 1 2 | 0 0 0 0 0 2 1 0 | * * * * * 3 *
...x3...x     | 0 0 0 6 | 0 0 0 0 0 0 3 3 | * * * * * * 1  {6}