Acronym	cont
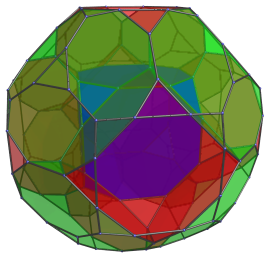
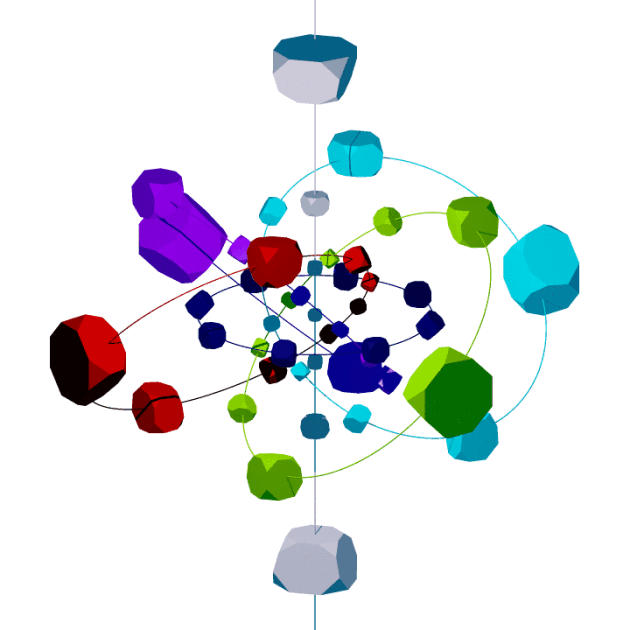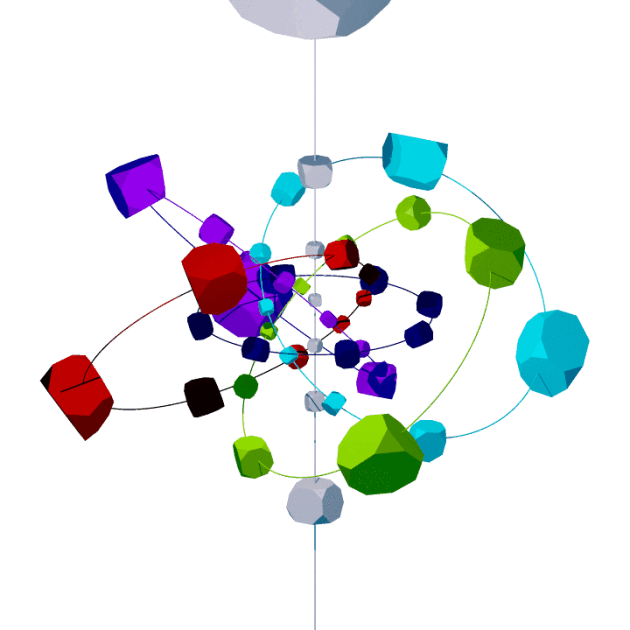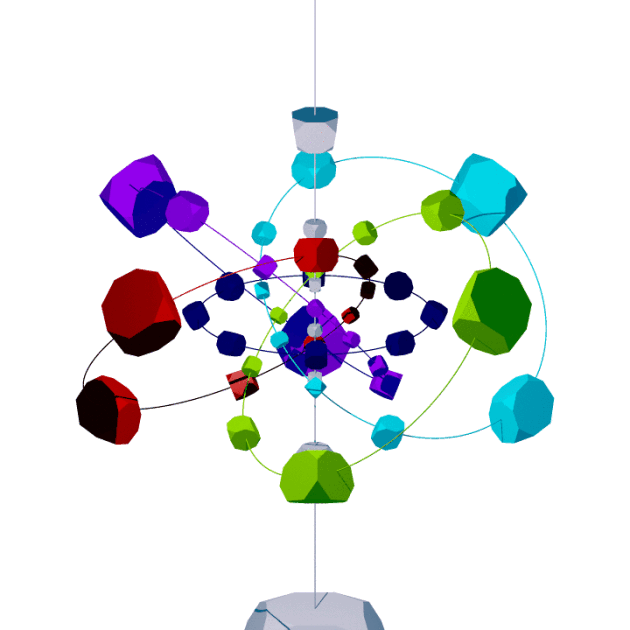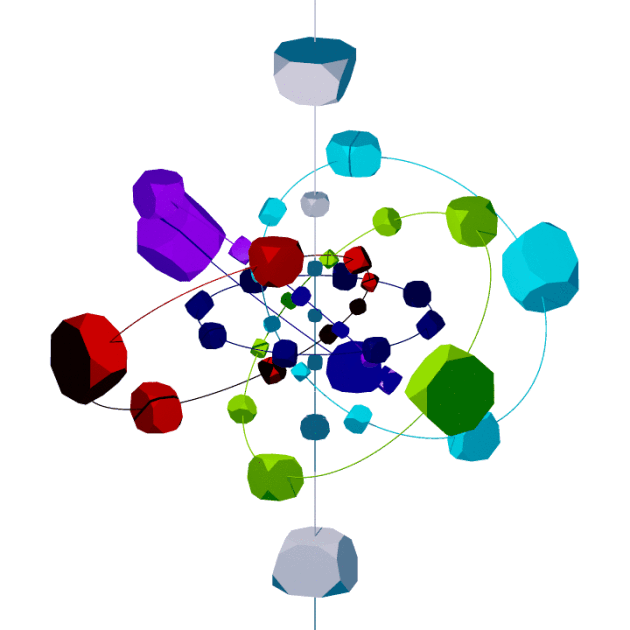
Name	tetracontoctachoron, octagonny, bitruncated icositetrachoron
	© © showing its relation to swirl symmetry
Cross sections	©
Circumradius	2+sqrt(2) = 3.414214
Vertex figure	©
Vertex layers	Layer Symmetry Subsymmetries   o3o4o3o o3o4o . o3o . o o . o3o . o4o3o 1 o3x4x3o o3x4x . tic first o3x . o {3} first o . x3o {3} first . x4x3o tic first 2 o3w4o . o3w . x x . w3o . o4w3o 3 x3w4o . x3w . w w . w3x . o4w3x 4 w3x4x . w3x . X X . x3w . x4x3w 5 w3o4w . w3w . w w . w3w . w4o3w 6 x3o4X . w3o . W W . o3w . X4o3x 7a w3o4w . X3w . x x . w3X . w4o3w 7b x3o . Y Y . o3x 8 w3x4x . W3x . o o . x3W . x4x3w 9 x3w4o . w3X . w w . X3w . o4w3x 10 o3w4o . w3o . Y Y . o3w . o4w3o 11 o3x4x . opposite tic x3W . w w . W3x . x4x3o opposite tic 12   Y3o . o o . o3Y   13 w3X . X X . X3w 14a o3Y . x x . Y3o 14b w3x . Y Y . x3w 15 w3w . W W . w3w 16a Y3o . x x . o3Y 16b x3w . Y Y . w3x 17 X3w . X X . w3X 18 o3Y . o o . Y3o 19 W3x . w w . x3W 20 o3w . Y Y . w3o 21 X3w . w w . w3X 22 x3W . o o . W3x 23a w3X . x x . X3w 23b o3x . Y Y . x3o 24 o3w . W W . w3o 25 w3w . w w . w3w 26 x3w . X X . w3x 27 w3x . w w . x3w 28 w3o . x x . o3w 29 x3o . o opposite {3} o . o3x opposite {3} (X=x+w=2x+q, W=2x+2q, Y=3x+2q)
Lace city in approx. ASCII-art	©   x4x w4o w4o x4x o4w X4o o4w o4w o4X X4x o4X o4w x4x x4X w4w w4w x4X x4x w4o w4w w4w w4o X4o X4x X4x X4o X=x+w=2x+q w4o w4w w4w w4o x4x x4X w4w w4w x4X x4x o4w o4X X4x o4X o4w o4w X4o o4w x4x w4o w4o x4x
	©   x3o w3o w3x x3w o3w o3x w3o w3w o3w w3x w3X X3w x3w x3w w3w w3X x3W W3x X3w w3w w3x o3w X3w o3Y Y3o w3X w3o X=wq=x+w=2x+q, W=2w=2x+2q, Y=ww=3x+2q o3x W3x Y3o o3Y x3W x3o o3w X3w o3Y Y3o w3X w3o x3w w3w w3X x3W W3x X3w w3w w3x w3x w3X X3w x3w w3o w3w o3w x3o w3o w3x x3w o3w o3x
General of army	(is itself convex)
Colonel of regiment	(is itself locally convex – uniform polychoral members: by cells: tic cont 48 )
Dihedral angles	at {8} between tic and tic:   135° at {3} between tic and tic:   120°
Dual	bicont
Face vector	288, 576, 336, 48
Confer	Grünbaumian relatives: 2cont   decompositions: srico || cont   ambification: recont   general polytopal classes: Wythoffian polychora   noble polytopes   partial Stott expansions
External links

As abstract polytope cont is isomorphic to gic, thereby replacing the octagons by octagrams, resp. replacing tic by quith.

Note that cont can be thought of as the external blend of 1 srico + 24 sircoatics + 96 triddips + 24 coatics. This decomposition is described as the degenerate segmentoteron xo3ox4xx3oo&#x.

As can be read from the matrices below, at every edge there are 2 octagons. Thus we get as pseudo cells something with octagons only. From the vertex incidence we further read off that this pseudo tiling happens to use 4 octagons per vertex. From the here truely being used cells (tic) it is deduced, that any straight edge sequence of that seeming x8o4o needs to be mod-wrapped to triangular holes. Therefore those pseudo cells rather are the skew polyhedron x8o4o|3 instead, which here happens to be finite of course (just 144 remaining such octagons).

By virtue of an outer symmetry this is a non-quasiregular monotoxal polychoron, that is all edges belong to the same equivalence class.

Incidence matrix according to Dynkin symbol

o3x4x3o

. . . . | 288 ♦   2   2 |  1   4  1 |  2  2
--------+-----+---------+-----------+------
. x . . |   2 | 288   * |  1   2  0 |  2  1
. . x . |   2 |   * 288 |  0   2  1 |  1  2
--------+-----+---------+-----------+------
o3x . . |   3 |   3   0 | 96   *  * |  2  0
. x4x . |   8 |   4   4 |  * 144  * |  1  1
. . x3o |   3 |   0   3 |  *   * 96 |  0  2
--------+-----+---------+-----------+------
o3x4x . ♦  24 |  24  12 |  8   6  0 | 24  *
. x4x3o ♦  24 |  12  24 |  0   6  8 |  * 24

or
. . . .    | 288 ♦   4 |   2   4 |  4
-----------+-----+-----+---------+---
. x . .  & |   2 | 576 |   1   2 |  3
-----------+-----+-----+---------+---
o3x . .  & |   3 |   3 | 192   * |  2
. x4x .    |   8 |   8 |   * 144 |  2
-----------+-----+-----+---------+---
o3x4x .  & ♦  24 |  36 |   8   6 | 48

snubbed forms: o3β4x3o, o3β4β3o

o3x4x3/2o

. . .   . | 288 ♦   2   2 |  1   4  1 |  2  2
----------+-----+---------+-----------+------
. x .   . |   2 | 288   * |  1   2  0 |  2  1
. . x   . |   2 |   * 288 |  0   2  1 |  1  2
----------+-----+---------+-----------+------
o3x .   . |   3 |   3   0 | 96   *  * |  2  0
. x4x   . |   8 |   4   4 |  * 144  * |  1  1
. . x3/2o |   3 |   0   3 |  *   * 96 |  0  2
----------+-----+---------+-----------+------
o3x4x   . ♦  24 |  24  12 |  8   6  0 | 24  *
. x4x3/2o ♦  24 |  12  24 |  0   6  8 |  * 24

o3/2x4x3/2o

.   . .   . | 288 ♦   2   2 |  1   4  1 |  2  2
------------+-----+---------+-----------+------
.   x .   . |   2 | 288   * |  1   2  0 |  2  1
.   . x   . |   2 |   * 288 |  0   2  1 |  1  2
------------+-----+---------+-----------+------
o3/2x .   . |   3 |   3   0 | 96   *  * |  2  0
.   x4x   . |   8 |   4   4 |  * 144  * |  1  1
.   . x3/2o |   3 |   0   3 |  *   * 96 |  0  2
------------+-----+---------+-----------+------
o3/2x4x   . ♦  24 |  24  12 |  8   6  0 | 24  *
.   x4x3/2o ♦  24 |  12  24 |  0   6  8 |  * 24

or
.   . .   .    | 288 ♦   4 |   2   4 |  4
---------------+-----+-----+---------+---
.   x .   .  & |   2 | 576 |   1   2 |  3
---------------+-----+-----+---------+---
o3/2x .   .  & |   3 |   3 | 192   * |  2
.   x4x   .    |   8 |   8 |   * 144 |  2
---------------+-----+-----+---------+---
o3/2x4x   .  & ♦  24 |  36 |   8   6 | 48

wx3oo3xw4xo&#zx   → height = 0
(tegum sum of (w,x,x)-proh and (x,w)-rico)

o.3o.3o.4o.     | 192  * ♦   2  1   1  0 |  1  2  2  1  0 | 1  1  2
.o3.o3.o4.o     |   * 96 ♦   0  0   2  2 |  0  0  4  1  1 | 0  2  2
----------------+--------+---------------+----------------+--------
.. .. x. ..     |   2  0 | 192  *   *  * |  1  1  1  0  0 | 1  1  1
.. .. .. x.     |   2  0 |   * 96   *  * |  0  2  0  1  0 | 1  0  2
oo3oo3oo4oo&#x  |   1  1 |   *  * 192  * |  0  0  2  1  0 | 0  1  2
.x .. .. ..     |   0  2 |   *  *   * 96 |  0  0  2  0  1 | 0  2  1
----------------+--------+---------------+----------------+--------
.. o.3x. ..     |   3  0 |   3  0   0  0 | 64  *  *  *  * | 1  1  0
.. .. x.4x.     |   8  0 |   4  4   0  0 |  * 48  *  *  * | 1  0  1
wx .. xw ..&#zx |   4  4 |   2  0   4  2 |  *  * 96  *  * | 0  1  1
.. .. .. xo&#x  |   2  1 |   0  1   2  0 |  *  *  * 96  * | 0  0  2
.x3.o .. ..     |   0  3 |   0  0   0  3 |  *  *  *  * 32 | 0  2  0
----------------+--------+---------------+----------------+--------
.. o.3x.4x.     ♦  24  0 |  24 12   0  0 |  8  6  0  0  0 | 8  *  *
wx3oo3xw ..&#zx ♦  12 12 |  12  0  12 12 |  4  0  6  0  4 | * 16  *
wx .. xw4xo&#zx ♦  16  8 |   8  8  16  4 |  0  2  4  8  0 | *  * 24