Acronym	bilbiro, J91
Name	bilunabirotunda
	© ©   ©
Vertex figures	[(3,5)2], [3,4,3,5], [3,52]
Lace city in approx. ASCII-art	x f f o o f f x
	o o x x f x x o o
	x x F where: o o F=ff=x+f F x x
Coordinates	(F/2, 1/2, 0)         & all changes of sign (1/2, f/2, 1/2)       & all changes of sign (0, 0, f/2)             & all changes of sign where f = (1+sqrt(5))/2 = 1.618034, F = (3+sqrt(5))/2 = 2.618034
General of army	(is itself convex)
Colonel of regiment	(is itself locally convex)
Dihedral angles	between {3} and {4} (lunal):   arccos(-(1+sqrt(5))/sqrt(12)) = 159.094843° between {3} and {5} (rotundal):   arccos(-sqrt[(5+2 sqrt(5))/15]) = 142.622632° between {3} and {4} (across rim):   arccos(-sqrt[(3-sqrt(5))/6]) = 110.905157° between {3} and {5} (across rim):   arccos(-sqrt[(5-2 sqrt(5))/15]) = 100.812317° between {5} and {5}:   arccos(1/sqrt(5)) = 63.434949°
Face vector	14, 26, 14
Confer	uniform relative: ike   id   srid   related Johnson solids: pocuro   pero   pecu   thawro   general polytopal classes: Johnson solids   expanded kaleido-facetings
External links

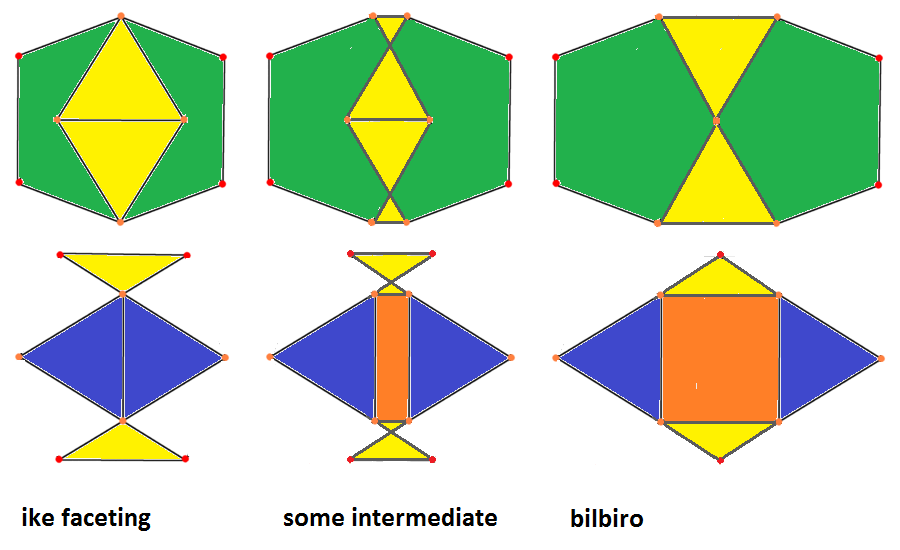
The right pic shows how bilbiro can be obtained by means of an expanded kaleido-faceting from ike. And this relation too is why bilbiro occures not too seldomly as a cell within CRFs.

This polyhedron is related also to id and srid, because in fact its surface could be decomposed into 4 regions (2 pentagons plus 2 triangles around a vertex each, respectively the lunes of a square and the 2 attached triangles), each of which either belong to the one or the other polyhedron.

As abstract polytope bilbiro is isomorphic to gibil biro, thereby replacing pentagons by pentagrams.

Incidence matrix according to Dynkin symbol

xfofx oxfxo&#xt   → outer heights = (1+sqrt(5))/4 = 0.809017
                    inner heights = 1/2
(line || pseudo (f,x)-{4} || pseudo ortho f-line || pseudo (f,x)-{4} || line)

o.... o....     | 2 * * * * | 1 2 0 0 0 0 0 0 0 | 1 2 0 0 0 0
.o... .o...     | * 4 * * * | 0 1 1 1 1 0 0 0 0 | 1 1 1 1 0 0
..o.. ..o..     | * * 2 * * | 0 0 0 2 0 2 0 0 0 | 0 1 0 2 1 0
...o. ...o.     | * * * 4 * | 0 0 0 0 1 1 1 1 0 | 0 0 1 1 1 1
....o ....o     | * * * * 2 | 0 0 0 0 0 0 0 2 1 | 0 0 0 0 2 1
----------------+-----------+-------------------+------------
x.... .....     | 2 0 0 0 0 | 1 * * * * * * * * | 0 2 0 0 0 0
oo... oo...&#x  | 1 1 0 0 0 | * 4 * * * * * * * | 1 1 0 0 0 0
..... .x...     | 0 2 0 0 0 | * * 2 * * * * * * | 1 0 1 0 0 0
.oo.. .oo..&#x  | 0 1 1 0 0 | * * * 4 * * * * * | 0 1 0 1 0 0
.o.o. .o.o.&#x  | 0 1 0 1 0 | * * * * 4 * * * * | 0 0 1 1 0 0
..oo. ..oo.&#x  | 0 0 1 1 0 | * * * * * 4 * * * | 0 0 0 1 1 0
..... ...x.     | 0 0 0 2 0 | * * * * * * 2 * * | 0 0 1 0 0 1
...oo ...oo&#x  | 0 0 0 1 1 | * * * * * * * 4 * | 0 0 0 0 1 1
....x .....     | 0 0 0 0 2 | * * * * * * * * 1 | 0 0 0 0 2 0
----------------+-----------+-------------------+------------
..... ox...&#x  | 1 2 0 0 0 | 0 2 1 0 0 0 0 0 0 | 2 * * * * *
xfo.. .....&#xt | 2 2 1 0 0 | 1 2 0 2 0 0 0 0 0 | * 2 * * * *
..... .x.x.&#x  | 0 2 0 2 0 | 0 0 1 0 2 0 1 0 0 | * * 2 * * *
.ooo. .ooo.&#xt | 0 1 1 1 0 | 0 0 0 1 1 1 0 0 0 | * * * 4 * *
..ofx .....&#xt | 0 0 1 2 2 | 0 0 0 0 0 2 0 2 1 | * * * * 2 *
..... ...xo&#x  | 0 0 0 2 1 | 0 0 0 0 0 0 1 2 0 | * * * * * 2

or
o.... o....      & | 4 * * | 1 2 0 0 0 | 1 2 0 0  [3,52]
.o... .o...      & | * 8 * | 0 1 1 1 1 | 1 1 1 1  [3,4,3,5]
..o.. ..o..        | * * 2 | 0 0 0 4 0 | 0 2 0 2  [(3,5)2]
-------------------+-------+-----------+--------
x.... .....      & | 2 0 0 | 2 * * * * | 0 2 0 0
oo... oo...&#x   & | 1 1 0 | * 8 * * * | 1 1 0 0
..... .x...      & | 0 2 0 | * * 4 * * | 1 0 1 0
.oo.. .oo..&#x   & | 0 1 1 | * * * 8 * | 0 1 0 1
.o.o. .o.o.&#x     | 0 2 0 | * * * * 4 | 0 0 1 1
-------------------+-------+-----------+--------
..... ox...&#x   & | 1 2 0 | 0 2 1 0 0 | 4 * * *
xfo.. .....&#xt  & | 2 2 1 | 1 2 0 2 0 | * 4 * *
..... .x.x.&#x     | 0 4 0 | 0 0 2 0 2 | * * 2 *
.ooo. .ooo.&#xt    | 0 2 1 | 0 0 0 2 1 | * * * 4

xFoFx xofox&#xt    → outer heights = (sqrt(5)-1)/4 = 0.309017
(F=ff=x+f)           inner heights = 1/2
({4} || pseudo F-line || pseudo ortho f-line || pseudo F-line || {4})

o.... o....     | 4 * * * * | 1 1 1 1 0 0 0 0 0 | 1 1 1 1 0 0 0
.o... .o...     | * 2 * * * | 0 0 2 0 1 0 0 0 0 | 0 1 0 2 0 0 0
..o.. ..o..     | * * 2 * * | 0 0 0 2 0 2 0 0 0 | 0 0 1 2 1 0 0
...o. ...o.     | * * * 2 * | 0 0 0 0 1 0 2 0 0 | 0 0 0 2 0 1 0
....o ....o     | * * * * 4 | 0 0 0 0 0 1 1 1 1 | 0 0 0 1 1 1 1
----------------+-----------+-------------------+--------------
x.... .....     | 2 0 0 0 0 | 2 * * * * * * * * | 1 0 1 0 0 0 0
..... x....     | 2 0 0 0 0 | * 2 * * * * * * * | 1 1 0 0 0 0 0
oo... oo...&#x  | 1 1 0 0 0 | * * 4 * * * * * * | 0 1 0 1 0 0 0
o.o.. o.o..&#x  | 1 0 1 0 0 | * * * 4 * * * * * | 0 0 1 1 0 0 0
.o.o. .o.o.&#x  | 0 1 0 1 0 | * * * * 2 * * * * | 0 0 0 2 0 0 0
..o.o ..o.o&#x  | 0 0 1 0 1 | * * * * * 4 * * * | 0 0 0 1 1 0 0
...oo ...oo&#x  | 0 0 0 1 1 | * * * * * * 4 * * | 0 0 0 1 0 1 0
....x .....     | 0 0 0 0 2 | * * * * * * * 2 * | 0 0 0 0 1 0 1
..... ....x     | 0 0 0 0 2 | * * * * * * * * 2 | 0 0 0 0 0 1 1
----------------+-----------+-------------------+--------------
x.... x....     | 4 0 0 0 0 | 2 2 0 0 0 0 0 0 0 | 1 * * * * * *
..... xo...&#x  | 2 1 0 0 0 | 0 1 2 0 0 0 0 0 0 | * 2 * * * * *
x.o.. .....&#x  | 2 0 1 0 0 | 1 0 0 2 0 0 0 0 0 | * * 2 * * * *
ooooo ooooo&#xt | 1 1 1 1 1 | 0 0 1 1 1 1 1 0 0 | * * * 4 * * *
..o.x .....&#x  | 0 0 1 0 2 | 0 0 0 0 0 2 0 1 0 | * * * * 2 * *
..... ...ox&#x  | 0 0 0 1 2 | 0 0 0 0 0 0 2 0 1 | * * * * * 2 *
....x ....x     | 0 0 0 0 4 | 0 0 0 0 0 0 0 2 2 | * * * * * * 1

or
o.... o....     & | 8 * * | 1 1 1 1 0 | 1 1 1 1  [3,4,3,5]
.o... .o...     & | * 4 * | 0 0 2 0 1 | 0 1 0 2  [3,52]
..o.. ..o..       | * * 2 | 0 0 0 4 0 | 0 0 2 2  [(3,5)2]
------------------+-------+-----------+--------
x.... .....     & | 2 0 0 | 4 * * * * | 1 0 1 0
..... x....     & | 2 0 0 | * 4 * * * | 1 1 0 0
oo... oo...&#x  & | 1 1 0 | * * 8 * * | 0 1 0 1
o.o.. o.o..&#x  & | 1 0 1 | * * * 8 * | 0 0 1 1
.o.o. .o.o.&#x    | 0 2 0 | * * * * 2 | 0 0 0 2
------------------+-------+-----------+--------
x.... x....     & | 4 0 0 | 2 2 0 0 0 | 2 * * *
..... xo...&#x  & | 2 1 0 | 0 1 2 0 0 | * 4 * *
x.o.. .....&#x  & | 2 0 1 | 1 0 0 2 0 | * * 4 *
ooooo ooooo&#xt   | 2 2 1 | 0 0 2 2 1 | * * * 4

oxFxo ofxfo&#xt   → outer heights = (sqrt(5)-1)/4 = 0.309017
(F=ff=x+f)           inner heights = 1/2
(pt || pseudo (x,f)-{4} || pseudo (F,x)-{4} || pseudo (x,f)-{4} || pt)

o.... o....     | 1 * * * * | 4 0 0 0 0 0 0 0 | 2 2 0 0 0 0
.o... .o...     | * 4 * * * | 1 1 1 1 0 0 0 0 | 1 1 1 1 0 0
..o.. ..o..     | * * 4 * * | 0 0 1 0 1 1 0 0 | 0 1 0 1 1 0
...o. ...o.     | * * * 4 * | 0 0 0 1 0 1 1 1 | 0 0 1 1 1 1
....o ....o     | * * * * 1 | 0 0 0 0 0 0 0 4 | 0 0 0 0 2 2
----------------+-----------+-----------------+------------
oo... oo...&#x  | 1 1 0 0 0 | 4 * * * * * * * | 1 1 0 0 0 0
.x... .....     | 0 2 0 0 0 | * 2 * * * * * * | 1 0 1 0 0 0
.oo.. .oo..&#x  | 0 1 1 0 0 | * * 4 * * * * * | 0 1 0 1 0 0
.o.o. .o.o.&#x  | 0 1 0 1 0 | * * * 4 * * * * | 0 0 1 1 0 0
..... ..x..     | 0 0 2 0 0 | * * * * 2 * * * | 0 1 0 0 1 0
..oo. ..oo.&#x  | 0 0 1 1 0 | * * * * * 4 * * | 0 0 0 1 1 0
...x. .....     | 0 0 0 2 0 | * * * * * * 2 * | 0 0 1 0 0 1
...oo ...oo&#x  | 0 0 0 1 1 | * * * * * * * 4 | 0 0 0 0 1 1
----------------+-----------+-----------------+------------
ox... .....&#x  | 1 2 0 0 0 | 2 1 0 0 0 0 0 0 | 2 * * * * *
..... ofx..&#xt | 1 2 2 0 0 | 2 0 2 0 1 0 0 0 | * 2 * * * *
.x.x. .....&#x  | 0 2 0 2 0 | 0 1 0 2 0 0 1 0 | * * 2 * * *
.ooo. .ooo.&#xt | 0 1 1 1 0 | 0 0 1 1 0 1 0 0 | * * * 4 * *
..... ..xfo&#xt | 0 0 2 2 1 | 0 0 0 0 1 2 0 2 | * * * * 2 *
...xo .....&#x  | 0 0 0 2 1 | 0 0 0 0 0 0 1 2 | * * * * * 2

or
o.... o....     & | 2 * * | 4 0 0 0 0 | 2 2 0 0  [(3,5)2]
.o... .o...     & | * 8 * | 1 1 1 1 0 | 1 1 1 1  [3,4,3,5]
..o.. ..o..       | * * 4 | 0 0 2 0 1 | 0 2 0 1  [3,52]
------------------+-------+-----------+--------
oo... oo...&#x  & | 1 1 0 | 8 * * * * | 1 1 0 0
.x... .....     & | 0 2 0 | * 4 * * * | 1 0 1 0
.oo.. .oo..&#x  & | 0 1 1 | * * 8 * * | 0 1 0 1
.o.o. .o.o.&#x    | 0 2 0 | * * * 4 * | 0 0 1 1
..... ..x..       | 0 0 2 | * * * * 2 | 0 2 0 0
------------------+-------+-----------+--------
ox... .....&#x  & | 1 2 0 | 2 1 0 0 0 | 4 * * *
..... ofx..&#xt & | 1 2 2 | 2 0 2 0 1 | * 4 * *
.x.x. .....&#x    | 0 4 0 | 0 2 0 2 0 | * * 2 *
.ooo. .ooo.&#xt   | 0 2 1 | 0 0 2 1 0 | * * * 4

fxo ofx oxF&#zxt   → both heights = 0
(F=ff=x+f)
(pseudo (f,o,o)-line || pseudo (x,f,x)-cube || pseudo (o,x,F)-{4})

o.. o.. o..     | 2 * * | 4 0 0 0 0 | 2 2 0 0  [(3,5)2]
.o. .o. .o.     | * 8 * | 1 1 1 1 0 | 1 1 1 1  [3,4,3,5]
..o ..o ..o     | * * 4 | 0 0 0 2 1 | 2 0 0 1  [3,52]
----------------+-------+-----------+--------
oo. oo. oo.&#x  | 1 1 0 | 8 * * * * | 1 1 0 0
.x. ... ...     | 0 2 0 | * 4 * * * | 0 0 1 1
... ... .x.     | 0 2 0 | * * 4 * * | 0 1 1 0
.oo .oo .oo&#x  | 0 1 1 | * * * 8 * | 1 0 0 1
... ..x ...     | 0 0 2 | * * * * 2 | 2 0 0 0
----------------+-------+-----------+--------
... ofx ...&#xt | 1 2 2 | 2 0 0 2 1 | 4 * * *
... ... ox.&#x  | 1 2 0 | 2 0 1 0 0 | * 4 * *
.x. ... .x.     | 0 4 0 | 0 2 2 0 0 | * * 2 *
.xo ... ...&#x  | 0 2 1 | 0 1 0 2 0 | * * * 4