Acronym	grit
Name	great rhombated tesseract, cantitruncated tesseract
Cross sections	©
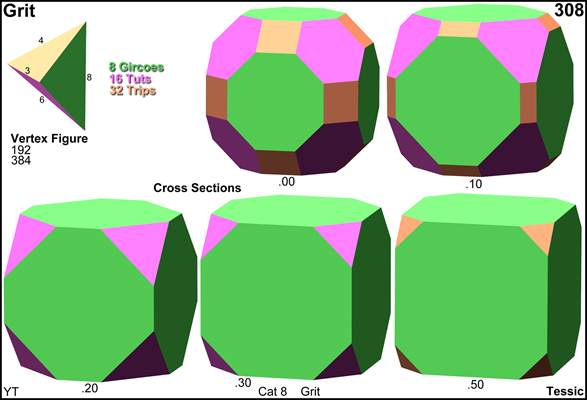Circumradius	sqrt[(11+5 sqrt(2))/2] = 3.005916
Vertex figure	©
Vertex layers	Layer Symmetry Subsymmetries   o3o3o4o o3o3o . o3o . o o . o4o . o3o4o 1 o3x3x4x o3x3x . tut first o3x . x trip first o . x4x {8} first . x3x4x girco first 2 o3x3w . o3u . w x . u4x . o3u4x 3 o3u3w . x3x . Q u . x4w . o3x4w 4 o3X3x . o3X . w x . o4Q . o3x4w 5a x3x3X . o3Y . x X . x4w . o3u4x 5b x3w . Q 6a x3w3u . x3Y . x w . o4Q . x3x4x opposite girco 6b u3w . Q Y . u4x 7 u3w3x . u3X . w Z . x4x   8a X3x3x . X3x . Q w . o4Q 8b Y . u4x 9 x3X3o . x3X . Q X . x4w 10 w3u3o . X3u . w x . o4Q 11a w3x3o . Y3x . x u . x4w 11b w3u . Q 12a x3x3o . opposite tut Y3o . x x . u4x 12b w3x . Q 13   X3o . w o . x4x opposite {8} 14 x3x . Q   15 u3o . w 16 x3o . x opposite trip (X=2x+q=u+q=x+w, Q=x+2q=w+q), Y=3x+q=u+w, Z=4x+q
Lace city in approx. ASCII-art	©   x4x u4x x4w x4w u4x x4x u4x o4Q o4Q u4x x4w o4Q o4Q x4w x4w o4Q o4Q x4w u4x o4Q o4Q u4x x4x u4x x4w x4w u4x x4x
	x3o x3o u3o u3o x3x x3x X3o X3o w3x Y3o Y3o w3x w3u Y3x Y3x w3u X3u X3u x3X x3X X3x X3x u3X u3X u3w x3Y x3Y u3w x3w o3Y o3Y x3w o3X o3X x3x x3x o3u o3u o3x o3x
Coordinates	((1+2 sqrt(2))/2, (1+2 sqrt(2))/2, (1+sqrt(2))/2, 1/2)   & all permutations, all changes of sign
General of army	(is itself convex)
Colonel of regiment	(is itself locally convex – uniform polychoral members: by cells: girco trip tut grit 8 32 16 )
Confer	2grit
External links

As abstract polytope grit is isomorphic to gaqrit, thereby replacing the octagons by octagrams, resp. replacing girco by quitco.

Incidence matrix according to Dynkin symbol

o3x3x4x

. . . . | 192 |   2  1  1 |  1  2  2  1 |  1  1 2
--------+-----+-----------+-------------+--------
. x . . |   2 | 192  *  * |  1  1  1  0 |  1  1 1
. . x . |   2 |   * 96  * |  0  2  0  1 |  1  0 2
. . . x |   2 |   *  * 96 |  0  0  2  1 |  0  1 2
--------+-----+-----------+-------------+--------
o3x . . |   3 |   3  0  0 | 64  *  *  * |  1  1 0
. x3x . |   6 |   3  3  0 |  * 64  *  * |  1  0 1
. x . x |   4 |   2  0  2 |  *  * 96  * |  0  1 1
. . x4x |   8 |   0  4  4 |  *  *  * 24 |  0  0 2
--------+-----+-----------+-------------+--------
o3x3x . ♦  12 |  12  6  0 |  4  4  0  0 | 16  * *
o3x . x ♦   6 |   6  0  3 |  2  0  3  0 |  * 32 *
. x3x4x ♦  48 |  24 24 24 |  0  8 12  6 |  *  * 8

o3/2x3x4x

.   . . . | 192 |   2  1  1 |  1  2  2  1 |  1  1 2
----------+-----+-----------+-------------+--------
.   x . . |   2 | 192  *  * |  1  1  1  0 |  1  1 1
.   . x . |   2 |   * 96  * |  0  2  0  1 |  1  0 2
.   . . x |   2 |   *  * 96 |  0  0  2  1 |  0  1 2
----------+-----+-----------+-------------+--------
o3/2x . . |   3 |   3  0  0 | 64  *  *  * |  1  1 0
.   x3x . |   6 |   3  3  0 |  * 64  *  * |  1  0 1
.   x . x |   4 |   2  0  2 |  *  * 96  * |  0  1 1
.   . x4x |   8 |   0  4  4 |  *  *  * 24 |  0  0 2
----------+-----+-----------+-------------+--------
o3/2x3x . ♦  12 |  12  6  0 |  4  4  0  0 | 16  * *
o3/2x . x ♦   6 |   6  0  3 |  2  0  3  0 |  * 32 *
.   x3x4x ♦  48 |  24 24 24 |  0  8 12  6 |  *  * 8

xoooox3xuxxux4xxwwxx&#xt   → height(1,2) = height(2,3) = height(4,5) = height(5,6) = 1/sqrt(2) = 0.707107
                             height(3,4) = 1
(girco || pseudo (x,u)-tic || pseudo (w,x)-tic || pseudo (w,x)-tic || pseudo (x,u)-tic || girco)

o.....3o.....4o.....      & | 96  *  * |  1  1  1  1  0  0  0  0 |  1  1  1  1  1  1  0  0  0 | 1  1  1 1 0
.o....3.o....4.o....      & |  * 48  * |  0  0  0  2  1  1  0  0 |  0  0  0  1  2  2  1  0  0 | 0  1  1 2 0
..o...3..o...4..o...      & |  *  * 48 |  0  0  0  0  0  1  2  1 |  0  0  0  0  2  0  1  1  2 | 0  1  0 2 1
----------------------------+----------+-------------------------+----------------------------+------------
x..... ...... ......      & |  2  0  0 | 48  *  *  *  *  *  *  * |  1  1  0  1  0  0  0  0  0 | 1  1  1 0 0
...... x..... ......      & |  2  0  0 |  * 48  *  *  *  *  *  * |  1  0  1  0  1  0  0  0  0 | 1  1  0 1 0
...... ...... x.....      & |  2  0  0 |  *  * 48  *  *  *  *  * |  0  1  1  0  0  1  0  0  0 | 1  0  1 1 0
oo....3oo....4oo....&#x   & |  1  1  0 |  *  *  * 96  *  *  *  * |  0  0  0  1  1  1  0  0  0 | 0  1  1 1 0
...... ...... .x....      & |  0  2  0 |  *  *  *  * 24  *  *  * |  0  0  0  0  0  2  1  0  0 | 0  0  1 2 0
.oo...3.oo...4.oo...&#x   & |  0  1  1 |  *  *  *  *  * 48  *  * |  0  0  0  0  2  0  1  0  0 | 0  1  0 2 0
...... ..x... ......      & |  0  0  2 |  *  *  *  *  *  * 48  * |  0  0  0  0  1  0  0  1  1 | 0  1  0 1 1
..oo..3..oo..4..oo..&#x     |  0  0  2 |  *  *  *  *  *  *  * 24 |  0  0  0  0  0  0  1  0  2 | 0  0  0 2 1
----------------------------+----------+-------------------------+----------------------------+------------
x.....3x..... ......      & |  6  0  0 |  3  3  0  0  0  0  0  0 | 16  *  *  *  *  *  *  *  * | 1  1  0 0 0
x..... ...... x.....      & |  4  0  0 |  2  0  2  0  0  0  0  0 |  * 24  *  *  *  *  *  *  * | 1  0  1 0 0
...... x.....4x.....      & |  8  0  0 |  0  4  4  0  0  0  0  0 |  *  * 12  *  *  *  *  *  * | 1  0  0 1 0
xo.... ...... ......&#x   & |  2  1  0 |  1  0  0  2  0  0  0  0 |  *  *  * 48  *  *  *  *  * | 0  1  1 0 0
...... xux... ......&#xt  & |  2  2  2 |  0  1  0  2  0  2  1  0 |  *  *  *  * 48  *  *  *  * | 0  1  0 1 0
...... ...... xx....&#x   & |  2  2  0 |  0  0  1  2  1  0  0  0 |  *  *  *  *  * 48  *  *  * | 0  0  1 1 0
...... ...... .xwwx.&#xt    |  0  4  4 |  0  0  0  0  2  4  0  2 |  *  *  *  *  *  * 12  *  * | 0  0  0 2 0
..o...3..x... ......      & |  0  0  3 |  0  0  0  0  0  0  3  0 |  *  *  *  *  *  *  * 16  * | 0  1  0 0 1
...... ..xx.. ......&#x     |  0  0  4 |  0  0  0  0  0  0  2  2 |  *  *  *  *  *  *  *  * 24 | 0  0  0 1 1
----------------------------+----------+-------------------------+----------------------------+------------
x.....3x.....4x.....      & ♦ 48  0  0 | 24 24 24  0  0  0  0  0 |  8 12  6  0  0  0  0  0  0 | 2  *  * * *
xoo...3xux... ......&#xt  & ♦  6  3  3 |  3  3  0  6  0  3  3  0 |  1  0  0  3  3  0  0  1  0 | * 16  * * *
xo.... ...... xx....&#x   & ♦  4  2  0 |  2  0  2  4  1  0  0  0 |  0  1  0  2  0  2  0  0  0 | *  * 24 * *
...... xuxxux4xxwwxx&#xt    ♦ 16 16 16 |  0  8  8 16  8 16  8  8 |  0  0  2  0  8  8  4  0  4 | *  *  * 6 *
..oo..3..xx.. ......&#x     ♦  0  0  6 |  0  0  0  0  0  0  6  3 |  0  0  0  0  0  0  0  2  3 | *  *  * * 8