Site Map Polytopes Dynkin Diagrams Vertex Figures, etc. Incidence Matrices Index

Lattices


M.C. Escher, "Cubic Space Division", ©

In contrast to tilings, honeycombs or tesselations of any other dimension, lattices are mere periodic point sets without any further elements and incidence structure. Periodicity here means, that whenever R1,0 is some being found point difference vector (R1,0 = r1 - r0), then not only q = r + R1,0 belongs to the same lattice for any lattice point r, but moreover any point qk = r + k R1,0 for any k ∈ ℤ. Now consider a corresponding difference vector subset, which makes up a base of the lattice. The whole lattice then happens to be nothing but the ℤ-span of that base. The base elements are called the primitive lattice vectors. For conveniance usually a lattice point at the origin is assumed, if not stated explicitly otherwise.

Most often a small change of coordinate values in the primitive vectors does not change the symmetry type of a lattice. A. Bravais not only listed these types for 3D, he also proved that there are exactly 14 of them (in that dimension). Accordingly the representants for either different symmetry type are nowadays called Bravais lattices, even within other dimensions.

A slightly larger vector subset than a mere base, in fact the closure of that base wrt. to reflection, then is called a root system. That is, whenever R and Q belongs to that set, then also does P, the reflection of Q wrt. to a hyperplane perpandicular to R. – Conversely, it is always possible to divide such a root system into 2 complemental subsets, a positive and a negative one. This can be done by selecting from a first direction either R or -R and then iteratively continuing this same selectioning under the additional restriction that for R and Q already being selected into one subset, that, whenever R + Q would be a root as well, then R + Q also has to be selected into the same. From these positive roots a still smaller subset of simple roots then can be defined in turn as those ones, which cannot be written as a sum of other positive ones. Such a set of simple roots then represents a lattice base again.

Most authors additionally distinguish between lattices and root lattices. But in view of the former definition of a root system there would be none. In fact those authors would include a further axiom into the notion of a root system. The complemental subset of authors instead would address that very notion as a crystallographic root system. This further axiom requires that for any Q, R from that root system (to be) the value 2 Q·R / R·R has to be an integer. I.e. Q and the reflection of Q wrt. to the hyperplane perpendicular to R have to produce a difference vector, which ought be an integral multiple of R. Accordingly, in view of the former paragraph, any lattice would be a root lattice. Whereas, in view of crystallography, only those, which bow to this additional restriction, can truely be attributed such. – Quite generally, any pair of roots provides that (then not necessarily integral) number. When being restricted to simple roots, i.e. a base, the set of those numbers in effect makes up a matrix, which is called the Cartan matrix. Note that this term, which is used as matrix entry, is clearly not symmetrical in R and Q; therefore the whole Cartan matrix too will not be symmetrical in general. – Sometimes also the mere matrix of the (unweighted) scalarproducts is referenced instead. That then is the associated Gram matrix. That one clearly is always symmetrical.

A further class of lattices is obtained by reciprocation. On the one hand the reciprocal lattice Λ* occurs by means of the Fourier transform of an according wavefunction based on any direct or position lattice Λ as the support for the resulting Bragg peaks in k-space. (By means of the quantum physical p = ℏk, that k-space sometimes also is refered to as momentum space.) In fact, when R is a period of the direct lattice, then also the wave functions of the two position vectors r resp. r + R ought provide the same values. Thus exp(i k·r) = exp(i k·(r+R)) = exp(i k·r) exp(i k·R), the last equal sign here just evaluates the rules of exponentiation, and therefore exp(i k·R) = 1. – Alternatively, and without that crystallographic referenece to Fourier transforms of wavefunctions, the reciprocal lattice can likewise be defined directly as Λ* = {k | k·R∈ℤ for all R∈Λ} (which then happens to coincide with the above description up to a global scaling factor of 2π). Within dimensions greater than 1 this k·R happens to be a scalar product, showing that generally corresponding base vectors of either space each have to have the same directions, but mutually being of inverse absolute size. – On the other hand this very mathematical description shows that the reciprocal of the reciprocal lattice then again happens to be the direct lattice again. And so there is no intrinsic preference between either one.

Wrt. (crystallographic) root lattices Λ the reciprocal lattice Λ* also is called a weight lattice. Right in this context it happens, that the root lattice itself always is a sublattice of its weight lattice. Moreover, the corresponding index | Λ* / Λ | is readily accessible by the determinant of the Cartan matrix of Λ. Weight lattices need no longer be crystallographic too, their Cartan matrix entries in general will become rationals. The exceptional lattices, where both are crystallographic, i.e. where | Λ* / Λ | = 1 (like for E8), are called unimodular.

Despite the fact that a lattice is a mere point set, there is a way how to associate a corresponding tesselation too. In fact, the Voronoi complex V(Λ) is a tesselation, defined by the individual Voronoi cells VR(Λ) are the closed subsets of embedding space (ℝ-span of Λ), which has lower or equal distance to some given lattice point R, than to any other one. The vertex set of the Voronoi complex, also refered to as the set of lattice holes, needs not be a lattice. That Voronoi complex moreover can be dualised (within that embedding space), resulting in the associated Delone complex D(Λ). The vertex set of this Delone complex for sure is the starting lattice again.

While within direct spaces to crystallographers the individual Voronoi cell also is known as Wigner-Size cell of the respective lattice, in reciprocal spaces it then is called its (first) Brillouin zone.


Root Lattices   (up)

Root lattices are closely related to Weyl groups. In fact, the rotational and translatoric symmetries of a lattice are described by the associated Weyl group. Conversely, just as the finite Coxeter groups provide polytopes, the infinite Weyl groups also provide flat n-dimensional euclidean tesselations, some of which re-occur here as Delone complexes of a corresponding lattice. It is a matter of fact, that Weyl groups and the associated lattices generally are labeled exactly the same by the first few capital letters of the alphabet and the dimension of the spanned space is given as its subscript. (Some authors however try to distinguish this a little by using different fonts for either usage.)

It shall be warned here though, that the usage of Bn and Cn in literature tends to be mutually inverted sometimes, both from author to author, or even within a single monograph from chapter to chapter. The here provided attribution of Weyl groups (and hence for the to be assciated lattices) however is in accordance to Coxeter.

Lattice Simple Roots & Notes Count & Hull of Roots Cartan matrix
Weyl group Voronoi complex V / Voronoi cell V0 Delone complex D / Delone cells Dk
An
(n ≥ 1)

The simplest way to describe An makes use of
An ≅ {∑ciei ∈ ℤn+1 | ∑ci = 0}, then:

  • ai = ei − ei+1   (1 ≤ i ≤ n)

A1 ≅ I1 ≅ ℤ
A2 ≅ G2
A2 ≅ ℤ[ω] = {a+bω | a,b∈ℤ},   ω = (-1+i√3)/2
      (Eisenstein integers)
A3 ≅ B3 ≅ fcc

| An* / An | = n+1 

1D:  2 - {}
2D:  6 - {6}
3D: 12 - co
4D: 20 - spid
5D: 30 - scad
6D: 42 - staf
7D: 56 - suph
8D: 72 - soxeb
...
nD: n(n+1)
       - x3o3o...3o3x  (n nodes, n≥1)
expanded simplex

 2 -1  0  0  0 ...
-1  2 -1  0  0 ...
 0 -1  2 -1  0 ...
 0  0 -1  2 -1 ...
 0  0  0 -1  2 ...
 ...

o3o3o...3o3*a  (n+1 nodes)

V(A1) ≅ aze     V0(A1) ≅ {}
V(A2) ≅ hexat   V0(A2) ≅ {6}
V(A3) ≅ radh    V0(A3) ≅ rad
...   ≅ ...     V0(A4) ≅ duspid

V0(An) ≅ xo..oo3ox..oo3...3oo..xo3oo..ox&#zy
         (n node positions, n layers)
         where y = x/sqrt(n+1)
       : projection of (n+1)-dim.
         hypercube along body-diagonal
       : m3o...o3m (i.e. dual of x3o...o3x)

D(A1) ≅ aze     D1(A1) ≅ {}
D(A2) ≅ trat    D1(A2) ≅ {3}
                D2(A2) ≅ dual {3}
D(A3) ≅ octet   D1(A3) ≅ tet
                D2(A3) ≅ oct
                D3(A3) ≅ dual tet
D(A4) ≅ cypit   D1(A4) ≅ pen
                D2(A4) ≅ rap
                D3(A4) ≅ inv rap
                D4(A4) ≅ dual pen
D(A5) ≅ cyxh    D1(A5) ≅ hix
                D2(A5) ≅ rix
                D3(A5) ≅ dot
                D4(A5) ≅ inv rix
                D5(A5) ≅ dual hix
D(A6) ≅ cyloh   D1(A6) ≅ hop
                D2(A6) ≅ ril
                D3(A6) ≅ bril
                D4(A6) ≅ inv bril
                D5(A6) ≅ inv ril
                D6(A6) ≅ dual hop
D(A7) ≅ cyooh   ...
...

D(An) ≅ x3o3o...3o3*a
        (n+1 nodes, n>1)
Dk(An) : k-th layer section of (n+1)-dim.
         hypercube perp. to body-diagonal
Cn
(n ≥ 2)
  • ai = ei − ei+1   (1 ≤ i ≤ n-1)
  • an = en

Cn ≅ (A1)n ≅ ℤn
primitive hypercubic

C2 ≅ ℤ[i] = {a+bi | a,b∈ℤ}
     (Gaußian integers)

| Cn* / Cn | = 2

(C1 = I1 ≅ A1 ≅ ℤ) 

large roots:
 2D:   4 - {4}
 3D:  12 - co
 4D:  24 - ico
 5D:  40 - rat
 6D:  60 - rag
 7D:  84 - rez
 8D: 112 - rek
 9D: 144 - riv
10D: 180 - rake
...
 nD: 2n(n-1)
         - o3x3o...3o4o  (n nodes, n>2)
rectified crosspolytope

small roots just point to:
 2D:  4 - side midpoints of {4},  i.e. dual {4}
 3D:  6 - centers of {4} of co,   i.e. oct
 4D:  8 - centers of some oct of ico, i.e. hex
 5D: 10 - centers of hex of rat,  i.e. tac
 6D: 12 - centers of tac of rag,  i.e. gee
 7D: 14 - centers of gee of rez,  i.e. zee
 8D: 16 - centers of zee of rek,  i.e. ek
 9D: 18 - centers of ek of riv,   i.e. vee
10D: 20 - centers of vee of rake, i.e. ka
...
 nD: 2n - centers of . x3o...3o4o
                  of o3x3o...3o4o
inscribed crosspolytope

     ...
...  2 -1  0  0  0
... -1  2 -1  0  0
...  0 -1  2 -1  0
...  0  0 -1  2 -2
...  0  0  0 -1  2

o4o3o3o...3o4o  (n+1 nodes, n>1)

V(C2) ≅ squat   V0(C2) ≅ {4}
V(C3) ≅ chon    V0(C3) ≅ cube
V(C4) ≅ test    V0(C4) ≅ tes
V(C5) ≅ penth   V0(C5) ≅ pent
V(C6) ≅ axh     V0(C6) ≅ ax
V(C7) ≅ hepth   V0(C7) ≅ hept
V(C8) ≅ och     V0(C8) ≅ octo
...

V(Cn) ≅ x4o3o3o...3o4o
        (n+1 nodes, n>1)
      : hypercubical honeycomb

D(C2) ≅ squat   D1(C2) ≅ {4}
D(C3) ≅ chon    D1(C3) ≅ cube
D(C4) ≅ test    D1(C4) ≅ tes
D(C5) ≅ penth   D1(C5) ≅ pent
D(C6) ≅ axh     D1(C6) ≅ ax
D(C7) ≅ hepth   D1(C7) ≅ hept
D(C8) ≅ och     D1(C8) ≅ octo
...

D(Cn) ≅ x4o3o3o...3o4o
        (n+1 nodes, n>1)
      : hypercubical honeycomb
Bn
(n ≥ 3)
  • ai = ei − ei+1   (1 ≤ i ≤ n-1)
  • an = 2 en

Bn ≅ {∑ciei ∈ ℤn+1 | ∑ci even}
Bn ≅ Dn
alternated hypercubic

B3 ≅ A3 ≅ fcc
B4 ≅ F4

| Bn* / Bn | = 2

(B2 = A1×A1 ≅ C2) 


 ©

large roots:
 3D:  6 - oct
 4D:  8 - hex
 5D: 10 - tac
 6D: 12 - gee
 7D: 14 - zee
 8D: 16 - ek
 9D: 18 - vee
10D: 20 - ka
...
 nD: 2n - x3o3o...3o4o  (n nodes, n>1)
crosspolytope

small roots just point to:
 3D:  12 - edge midpoints of oct, i.e. co
 4D:  24 - edge midpoints of hex, i.e. ico
 5D:  40 - edge midpoints of tac, i.e. rat
 6D:  60 - edge midpoints of gee, i.e. rag
 7D:  84 - edge midpoints of zee, i.e. rez
 8D: 112 - edge midpoints of ek,  i.e. rek
 9D: 144 - edge midpoints of vee, i.e. riv
10D: 180 - edge midpoints of ka,  i.e. rake
...
 nD: 2n(n-1)
         - centers of x . .... . .
                   of x3o3...o3o4o
inscribed rectified crosspolytope

     ...
...  2 -1  0  0  0
... -1  2 -1  0  0
...  0 -1  2 -1  0
...  0  0 -1  2 -1
...  0  0  0 -2  2

o3o3o *b3o...3o4o  (n+1 nodes, n>3)

V(B3) ≅ radh    V0(B3) ≅ rad
V(B4) ≅ icot    V0(B4) ≅ ico
...

V0(Bn) ≅ qo3oo3...3oo4ox&#zy
         (n node positions)
         where y = x sqrt(n+1)/2

D(B3) ≅ octet   D1(B3) ≅ tet
                D2(B3) ≅ oct
D(B4) ≅ hext    D1(B4) ≅ hex
D(B5) ≅ hinoh   D1(B5) ≅ hin
                D2(B5) ≅ tac
D(B6) ≅ haxh    D1(B6) ≅ hax
                D2(B6) ≅ gee
...

D(Bn) ≅ x3o3o *b3o...3o4o
        (n+1 nodes, n>2)
      : demi-hypercubical honeycomb
Dn
(n ≥ 4)
  • ai = ei − ei+1   (1 ≤ i ≤ n-1)
  • an = en-1 + en

Dn ≅ {∑ciei ∈ ℤn | ∑ci even}
Dn ≅ Bn
alternated hypercubic

D4 ≅ F4

| Dn* / Dn | = 4

(D3 = A3 ≅ B3 ≅ fcc) 

 4D:  24 - ico
 5D:  40 - rat
 6D:  60 - rag
 7D:  84 - rez
 8D: 112 - rek
 9D: 144 - riv
10D: 180 - rake
...
 nD: 2n(n-1)
         - o3x3o...3o4o  (n nodes, n>2)
rectified crosspolytope

     ...
...  2 -1  0  0  0
... -1  2 -1  0  0
...  0 -1  2 -1 -1
...  0  0 -1  2  0
...  0  0 -1  0  2

o3o3o o3o3o *b3o...3*e  (n+1 nodes, n>4)
resp.
o3o3o *b3o *b3o  (n=4)

V(D4) ≅ icot    V0(D4) ≅ ico
...

V0(Dn) ≅ xoo3ooo3oxo *b3ooo...ooo3oox&#zy
         (n node positions)
         where y = x sqrt[(n+1)/8]

D(D4) ≅ hext    D1(D4) ≅ hex
D(D5) ≅ hinoh   D1(D5) ≅ hin
                D2(D5) ≅ tac
D(D6) ≅ haxh    D1(D6) ≅ hax
                D2(D6) ≅ gee
...

D(Dn) ≅ x3o3o o3o3o *b3o...3*e
        (n+1 nodes, n>4)
      : demi-hypercubical honeycomb
E6
  • ai = ei − ei+1   (1 ≤ i ≤ 4)
  • a5 = e4 + e5
  • a6 = (−∑i<6ei + √3e6)/2

| E6* / E6 | = 3

(E5 = D5
 E4 = A4
 E3 = A2×A1) 

72 - mo
   - o3o3o3o3o *c3x
Gosset polypeton 12,2

 2 -1  0  0  0  0
-1  2 -1  0  0  0
 0 -1  2 -1 -1  0
 0  0 -1  2  0  0
 0  0 -1  0  2 -1
 0  0  0  0 -1  2

o3o3o3o3o *c3o3o

V(E6) ≅ reciprocal(22,2)

D(E6) ≅ jakoh        D1(E6) ≅ jak
Gosset hexacomb 22,2  Gosset polypeton 22,1
                      D2(E6) ≅ gyrated jak
                      Gosset polypeton 21,2
E7
  • ai = ei − ei+1   (1 ≤ i ≤ 5)
  • a6 = e5 + e6
  • a7 = (−∑i<7ei + √2e7)/2

| E7* / E7 | = 2 

126 - laq
    - x3o3o3o *c3o3o3o
Gosset polyexon 23,1

 2 -1  0  0  0  0  0
-1  2 -1  0  0  0  0
 0 -1  2 -1  0  0  0
 0  0 -1  2 -1 -1  0
 0  0  0 -1  2  0  0
 0  0  0 -1  0  2 -1
 0  0  0  0  0 -1  2

o3o3o3o3o3o3o *d3o

...

D(E7) ≅ naquoh        D1(E7) ≅ oca
Gosset heptacomb 33,1  Gosset polyexon 33,0
                       (= simplex)
                       D2(E7) ≅ naq
                       Gosset polyexon 32,1
E8
  • ai = ei − ei+1   (1 ≤ i ≤ 6)
  • a7 = e6 + e7
  • a8 = (−∑i<8ei + e8)/2

| E8* / E8 | = 1 

240 - fy
    - o3o3o3o *c3o3o3o3x
Gosset polyzetton 42,1

 2 -1  0  0  0  0  0  0
-1  2 -1  0  0  0  0  0
 0 -1  2 -1  0  0  0  0
 0  0 -1  2 -1  0  0  0
 0  0  0 -1  2 -1 -1  0
 0  0  0  0 -1  2  0  0
 0  0  0  0 -1  0  2 -1
 0  0  0  0  0  0 -1  2

o3o3o3o *c3o3o3o3o3o

...

D(E8) ≅ goh          D1(E8) ≅ ene
Gosset octacomb 52,1  Gosset polyzetton 52,0
                      (= simplex)
                      D2(E8) ≅ ek
                      Gosset polyzetton 51,1
                      (= cross-polytope)
F4
  • ai = ei − ei+1   (1 ≤ i ≤ 2)
  • a3 = e3
  • a4 = (−∑i<4ei + e4)/2

F4 ≅ B4 ≅ D4

| F4* / F4 | = 1 

large roots:
24 - ico

small roots:
24 - centers of oct of ico
inscribed dually oriented ico

 2 -1  0  0
-1  2 -2  0
 0 -1  2 -1
 0  0 -1  2

o3o3o4o3o

V(F4) ≅ icot
      : icositetrachoric tetracomb

D(F4) ≅ hext
      : hexadecachoric tetracomb
G2

One way to describe G2 makes use of
G2 ≅ {∑ciei ∈ ℤ3 | ∑ci = 0}, then:

  • a1 = e1 − e2
  • a2 = -2e1 + e2 + e3

G2 ≅ A2
G2 ≅ ℤ[ω] = {a+bω | a,b∈ℤ},   ω = (-1+i√3)/2
      (Eisenstein integers)

| G2* / G2 | = 1 

large roots:
6 - u6o

small roots:
6 - o6x
dual hexagon of halved sides

 2 -1
-3  2

o3o6o

V(G2) ≅ hexat = o3o6x

D(G2) ≅ trat = x3o6o
I1
  • a1 = e1

I1 = ℤ ≅ A1 ≅ B1 ≅ C1

| I1* / I1 | = 1 

2 - x

2

o-∞-o

V(I1) ≅ o-∞-x

D(I1) ≅ x-∞-o
reducible
Λ × Λ'
  • ai = (ai(Λ), 0)   (i ≤ d = dim(Λ))
  • ad+j = (0, aj(Λ'))   (j ≤ dim(Λ')) 
N(Λ) ⊕ N(Λ') - ...
tegum product of components

Cart(Λ)    0    
   0    Cart(Λ')

Weyl(Λ) × Weyl(Λ')

V(Λ × Λ') ≅ V(Λ) × V(Λ')
honeycomb product of components

eg. V(A2×A2) = o3o6x o3o6x (hibbit)

D(Λ × Λ') ≅ D(Λ) × D(Λ')
honeycomb product of components

eg. D(A2×A2) = x3o6o x3o6o (tribbit)

The latter entry shows that the individual Voronoi cells will be isohedral, iff the lattice is a root lattice or a direct product of identical root lattices.


Weight Lattices   (up)

A directly constructed base for the dual lattices can easily be derived from its associated original one: If B is the matrix of column vectors of the original lattice base, then A = (B-1)T clearly is the matrix of column vectors of the reciprocal lattice. (For, the scalar products, required in the definition of the reciprocal lattice, are just the entries of the matrix ATB, which, by the above choice, just happens to be the identity matrix.)

On the other hand, for weight lattices we know already that the corresponding root lattice defines a subset of points. Thus it might be more direct to provide the further generators only, instead.

Lattice Quotient Further generator(s) Overlay as compounded vertex set
Voronoi complex V / Voronoi cell V0 Delone complex D / Delone cells Dk
An*
(n ≥ 1)

An* / An ≅ ℤn+1

Just as An was best
understood as section
of Cn+1 perpendicular
to its body diagonal,
An* is obtained as
projection of Cn+1
along this direction.

A1* ≅ A1 ≅ ℤ
A2* ≅ A2 (rotoscaled)
A3* ≅ C3* ≅ D3* ≅ bcc

  • g = (e1 + ... + en − n en+1) / (n+1) 
xoo...o-3-oxo...o-3-oox...o- ... -ooo...x-3-*a

(n+1 compound components, n+1 node positions) 

V(A1*) ≅ aze       V0(A1*) ≅ {}
V(A2*) ≅ hexat     V0(A2*) ≅ {6}
V(A3*) ≅ batch     V0(A3*) ≅ toe
V(A4*) ≅ otcypit   V0(A4*) ≅ gippid
V(A5*) ≅ gapcyxh   V0(A5*) ≅ gocad
V(A6*) ≅ otcyloh  V0(A6*) ≅ gotaf
...                V0(A7*) ≅ guph
                   V0(A8*) ≅ goxeb
                   ...

V(An*) ≅ x3x3...x3*a (n+1 nodes)

V0(An*) is also known as the n-dimensional permutotope 
of order n+1, as its vertices represent all permutations of n+1
elements, while its edges correspond to their transpositions.

D(A1*) ≅ aze
D(A2*) ≅ trat
D(A3*) ≅ bichon
...
Cn*
(n ≥ 2)

Cn* / Cn ≅ ℤ2

bodycentered hypercubic

C2* ≅ C2 (rotoscaled)
C3* ≅ A3* ≅ bcc
Cn* ≅ Dn*

  • g = (e1 + ... + en) / 2 
xo-4-oo-3-oo- ... -oo-4-ox

V(C2*) ≅ squat    V0(C2*) ≅ {4}
V(C3*) ≅ batch    V0(C3*) ≅ toe
V(C4*) ≅ icot     V0(C4*) ≅ ico
V(C5*) ≅ titanoh  V0(C5*) ≅ bittit
V(C6*) ≅ traxh    V0(C6*) ≅ brag
...               V0(C7*) ≅ totaz
                  V0(C8*) ≅ tark
                  ...

V(C2m*) ≅ o4o3o...o3x3o...o3o4o
V(C2m+1*) ≅ o4o3o...o3x3x3o...o3o4o
(m>1 nodes unringed on either side) 
V(C2*) ≅ o4x4o
V(C3*) ≅ o4x3x4o
(m=1) 
D(C2*) ≅ squat
D(C3*) ≅ bichon
...
Bn*
(n ≥ 3)

Bn* / Bn ≅ ℤ2

primitive hypercubic

Bn* ≅ Cn ≅ (A1)n ≅ ℤn

  • g = en 
xo-3-oo-3-ox *b3-oo-...-oo-4-oo
(n+1 node positions, n≥3) 
V(B3*) ≅ chon    V0(B3*) ≅ cube
V(B4*) ≅ test    V0(B4*) ≅ tes
V(B5*) ≅ penth   V0(B5*) ≅ pent
V(B6*) ≅ axh     V0(B6*) ≅ ax
V(B7*) ≅ hepth   V0(B7*) ≅ hept
V(B8*) ≅ och     V0(B8*) ≅ octo
...

V(Bn*) ≅ o3o3o *b3o...o3o4x

D(B3*) ≅ chon    D1(B3*) ≅ cube
D(B4*) ≅ test    D1(B4*) ≅ tes
D(B5*) ≅ penth   D1(B5*) ≅ pent
D(B6*) ≅ axh     D1(B6*) ≅ ax
D(B7*) ≅ hepth   D1(B7*) ≅ hept
D(B8*) ≅ och     D1(B8*) ≅ octo
...
Dn*
(n ≥ 4)

Dn* / Dn ≅ ℤ4 (n odd)
Dn* / Dn ≅ ℤ2×ℤ2 (n even)

bodycentered hypercubic

Dn* ≅ Cn*

  • g1 = (e1 + ... + en) / 2
  • g2 = (e1 + ... + en-1 - en) / 2 
xooo-3-oooo-3-oxoo ooxo-3-oooo-3-ooox *b-3-oooo-....-oooo-3*e
(n+1 node positions, n>4) 
xooo-3-oooo-3-oxoo *b-3-ooxo *b-3-ooox
(n=4) 
V(D4*) ≅ icot     V0(D4*) ≅ ico
V(D5*) ≅ titanoh  V0(D5*) ≅ bittit
V(D6*) ≅ traxh    V0(D6*) ≅ brag
...               V0(D7*) ≅ totaz
                  V0(D8*) ≅ tark
                  ...

V(D2m*) ≅ o3o3o o3o3o *b3o...o3x3o...o3*e
V(D2m+1*) ≅ o3o3o o3o3o *b3o...o3x3x3o...o3*e
(m>2 nodes unringed on either side) 
V(D4*) ≅ o3x3o *b3o *b3o
V(D5*) ≅ o3x3o o3x3o *b3*e
(m=2) 
...
E6*

E6* / E6 ≅ ℤ3

  • g1 = ...
  • g2 = ... 
xoo-3-ooo-3-ooo-3-ooo-3-oxo *c-3-ooo-3-oox

V(E6*) ≅ ramoh         V0(E6*) ≅ ram
Gosset hexacomb 02,2,2  Gosset polypeton 02,2,1

...
E7*

E7* / E7 ≅ ℤ2

  • g = (e1 + ... + e6) / 2 
xo-3-oo-3-oo-3-oo-3-oo-3-oo-3-ox *d-3-oo

V(E7*) ≅ linoh        V0(E7*) ≅ lin
Gosset heptacomb 13,3  Gosset polyexon 13,2

...

The cases E8* ≅ E8, F4* ≅ F4, G2* ≅ G2, and I1* ≅ I1 can be omitted in the above table for obvious reasons.

Waterman polytopes   (up)

In 1990 Steve Waterman came up with an idea, which, generalized in the comunity of the Polyhedron Maillist Archive in November 2006, then became known as the (generalized) waterman polyhedra – or even more general: polytopes. This idea simply starts with any lattice (while Waterman originally considered FCC only) plus any "center point" chosen somewhere therein. Next a sphere of some given radius around that center point will select a (finite) subset of contained lattice points. The hull of these selected points then is the respective waterman polyhedron.

As it is obvious, the more symmetrically chosen "center points", like the lattice points themselves or the (shallow, deep, ...) holes etc., would result within more interesting, i.e. more symmetrical polyhedra, while more general "center points" would produce less interesting, asymmetrical polyhedra. Note further that this setup, while outlined above wrt. 3D lattices only, does well extend to any dimension likewise.

A small interactive VRML in those days was designed, displaying the contained point sets for the 3D primitive cubic, face-centered cubic, and body-centered cubic lattice wrt. the center point being a lattice point, as well as the former two thereof wrt. the center being a hole and a deep hole respectively. (The polyhedra according to the shallow holes in the second and the holes in the latter case would turn out subsymmetrical only and thence then got not displayed therein, however get listed below.)

The counts of contained lattice points each provide distinct discrete series wrt. continuously increasing radius, when considered for specific lattices and center points. Several of such series already are listed within the online encyclopedia of integer sequences and hence get refered below by their OEIS number accordingly.

2D Lattice Center Number min. Radius Count of points Hull Example
C2 (squat)
unit = square edge 		lattice point
(full o4o sym.) 		0 0 1 o4o - point
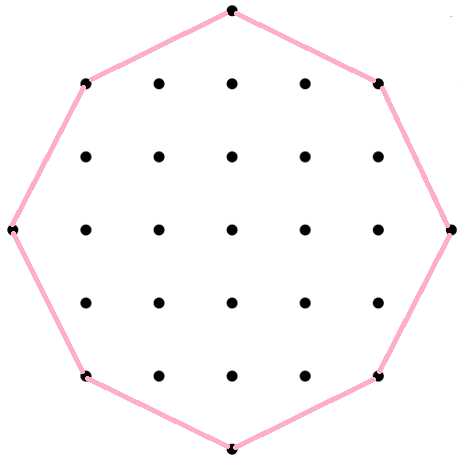Uo4oD&#zh
1 1 +4 = 5 o4q - square
2 sqrt(2) = 1.414214 +4 = 9 u4o - square
3 2 +4 = 13 o4Q - square
with Q = 2q = 2sqrt(2)
4 sqrt(5) = 2.236068 +8 = 21 u4q
5 sqrt(8) = 2.828427 +4 = 25 U4o - square
with U = 2u = 4
6 3 +4 = 29 Uo4oD&#zh
with D = dq = 3sqrt(2), U = 2u = 4
7 sqrt(10) = 3.162278 +8 = 37 u4Q
with Q = 2q = 2sqrt(2)
8 sqrt(13) = 3.605551 +8 = 45 U4q
with U = 2u = 4
... OEIS A057961  
hole
(full o4o sym.) 		1 1/sqrt(2) = 0.707107 4 x4o - square
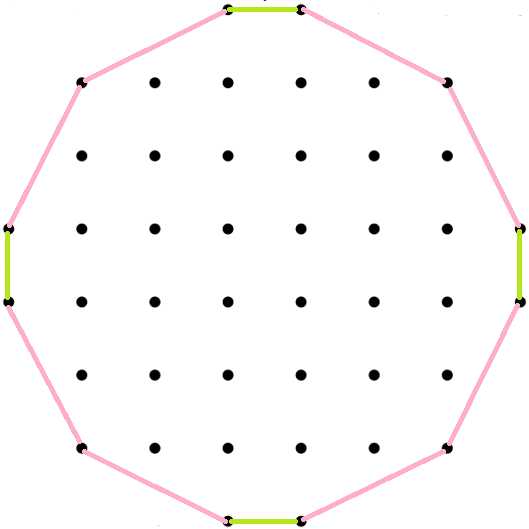Px4oD&#zh
2 sqrt(5/2) = 1.581139 +8 = 12 x4q
3 3/sqrt(2) = 2.121320 +4 = 16 d4o - square
with d = 3
4 sqrt(13/2) = 2.549510 +8 = 24 x4Q
with Q = 2q = 2sqrt(2)
5 sqrt(17/2) = 2.915476 +8 = 32 d4q
with d = 3
6 5/sqrt(2) = 3.535534 +12 = 44 Px4oD&#zh
with P = 5, D = dq = 3sqrt(2)
7 sqrt(29/2) = 3.807887 +8 = 52 d4Q
with d = 3, Q = 2q = 2sqrt(2)
... OEIS A057962  
A2 (trat)
unit = square edge 		lattice point
(full o6o sym.) 		0 0 1 o6o - point
1 1 +6 = 7 x6o - hexagon
2 sqrt(3) = 1.732051 +6 = 13 o6h - hexagon
3 2 +6 = 19 u6o - hexagon
4 sqrt(7) = 2.645751 +12 = 31 x6h
5 3 +6 = 37 d6o - hexagon
with d = 3
6 sqrt(12) = 3.464102 +6 = 43 o6H - hexagon
with H = 2h = 2sqrt(3)
7 sqrt(13) = 3.605551 +12 = 55 u6h
8 4 +6 = 61 U6o - hexagon
with U = 2u = 4
... OEIS A038590  
hole
(full o3o sym.) 		1 1/sqrt(3) = 0.577350 3 x3o - triangle
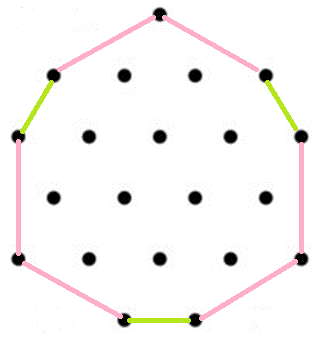Ux3od&#zh

do3uP&#zh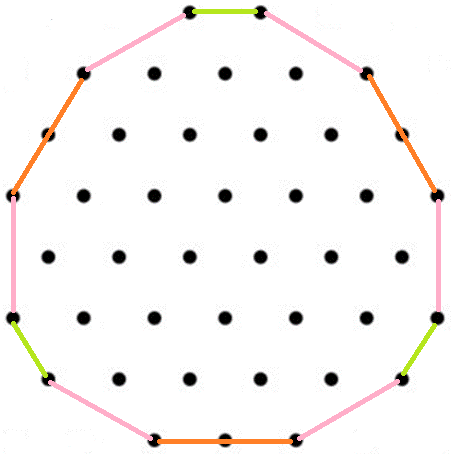

uP3Ux&#zh
2 sqrt(7/3) = 1.527525 +9 = 12 u3x
3 sqrt(13/3) = 2.081666 +6 = 18 x3d
with d = 3
4 4/sqrt(3) = 2.309401 +3 = 21 Ux3od&#h
with d = 3, U = 2u = 4
5 sqrt(19/3) = 2.516611 +6 = 27 d3u
with d = 3
6 5/sqrt(3) = 2.886751 +3 = 30 do3uP&#zh
with d = 3, P = 5
7 sqrt(28/3) = 3.055050 +6 = 36 u3U
with U = 2u = 4
8 sqrt(31/3) = 3.214550 +6 = 42 uP3Ux&#zh
with U = 2u = 4, P = 5
...

3D Lattice Center Number min. Radius Count of points Hull Example
C3 (primitive cubic)
unit = cube edge 		lattice point
(full o3o4o sym.) 		0 0 1 point
Zo3oq4ou&#zb
1 1 +6 = 7 q3o4o - oct
2 sqrt(2) = 1.414214 +12 = 19 o3q4o - co
3 sqrt(3) = 1.732051 +8 = 27 o3o4u - cube
4 2 +6 = 33 Qo3oo4ou&#zh - rad
with Q = 2sqrt(2) (pseudo)
5 sqrt(5) = 2.236068 +24 = 57 q3q4o - toe
6 sqrt(6) = 2.449490 +24 = 81 q3o4u
7 sqrt(8) = 2.828427 +12 = 93 o3Q4o - co
8 3 +30 = 123 Zo3oq4ou&#zb
where: Z = 3sqrt(2) (pseudo), b = sqrt(6)
... OEIS A117609  
hole
(full o3o4o sym.) 		1 sqrt(3)/2 = 0.866025 8 o3o4x - cube  
2 sqrt(11)/2 = 1.658312 +24 = 32 q3o4x
3 sqrt(19)/2 = 2.179449 +24 = 56 o3q4x
4 sqrt(27)/2 = 2.598076 +32 = 88 Qo3oo4xd&#zh
where: Q = 2sqrt(2) and d = 3 (pseudo)
5 sqrt(35)/2 = 2.958040 +48 = 136 q3q4x
...
A3 (face-centered cubic)
unit = root 		lattice point
(full o3o4o sym.) 		0 0 1 point
ax3ox4oq&#zh
1 1 +12 = 13 o3x4o - co
2 sqrt(2) = 1.414214 +6 = 19 u3o4o - oct
3 sqrt(3) = 1.732051 +24 = 43 reco
4 2 +12 = 55 o3u4o - co
5 sqrt(5) = 2.236068 +24 = 79 u3x4o
6 sqrt(6) = 2.449490 +8 = 87 uo3xo4oQ&#zh
where: Q = 2sqrt(2) (pseudo)
7 sqrt(7) = 2.645751 +48 = 135 x3x4q
8 sqrt(8) = 2.828427 +6 = 141 ax3ox4oq&#zh
where: a = 4 (pseudo)
9 3 +36 = 177 od3do4oq&#zh
where: d = 3 (pseudo)
10 sqrt(10) = 3.162278 +24 = 201 u3u4o - toe
... OEIS A119869  
deep hole
(full o3o4o sym.) 		1 1/sqrt(2) = 0.707107 6 x3o4o - oct
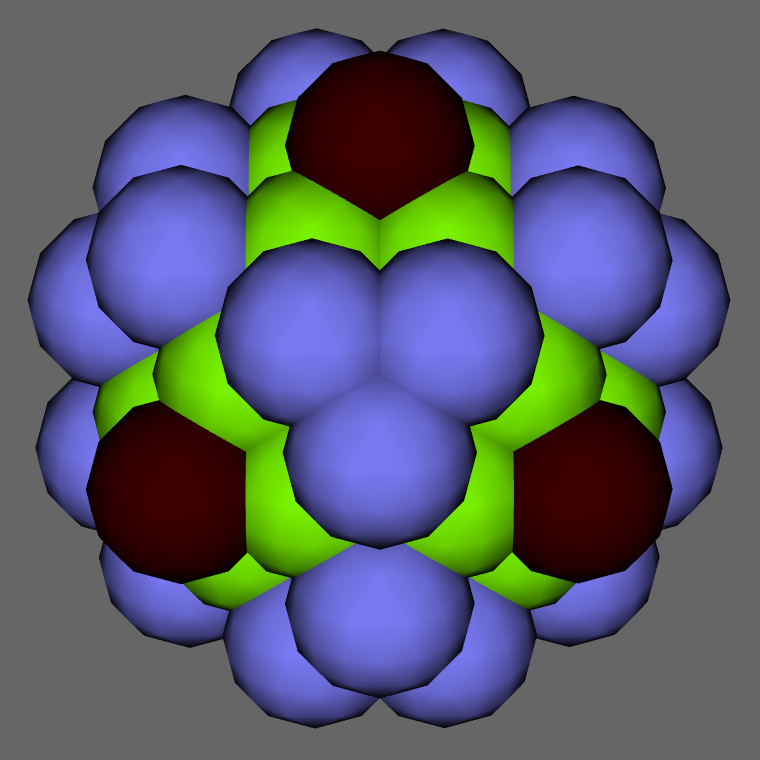do3ox4oq&#zh
2 sqrt(3/2) = 1.224745 +8 = 14 o3o4q - cube
3 sqrt(5/2) = 1.581139 +24 = 38 x3x4o - toe
4 3/sqrt(2) = 2.121320 +30 = 68 do3ox4oq&#zh
where: d = 3 (pseudo)
... OEIS A119874  
shallow hole
(o3o3o subsym.) 		1 sqrt(3/8) = 0.612372 4 x3o3o - tet  
2 sqrt(11/8) = 1.172604 +12 = 16 x3x3o - tut
3 sqrt(19/8) = 1.541104 +12 = 28 u3o3x
4 sqrt(27/8) = 1.837117 +16 = 44 ox3ou3do&#zh
where: d = 3 (pseudo)
5 sqrt(35/8) = 2.091650 +24 = 68 x3x3u
... OEIS A121054  
C3* (body-centered cubic)
unit = cube edge 		lattice point
(full o3o4o sym.) 		0 0 1 point
qo3qq4ox&#zc
1 sqrt(3)/2 = 0.866025 +8 = 9 o3o4x - cube
2 1 +6 = 15 qo3oo4ox&#zc - rad
where: c = sqrt(3)/2, q (pseudo)
3 sqrt(2) = 1.414214 +12 = 27 o3q4o - co
4 sqrt(11)/2 = 1.658312 +24 = 51 q3o4x
5 sqrt(3) = 1.732051 +8 = 59 oq3oo4ux&zc
where: c = sqrt(3)/2; q and u (pseudo)
6 2 +6 = 65 Qo3oo4ou&#zh - rad
where: Q = 2sqrt(2) (pseudo)
7 sqrt(19)/2 = 2.179449 +24 = 89 Qo3oq4ox&#ze
where: Q = 2sqrt(2) (pseudo), e = sqrt(11)/2
8 sqrt(5) = 2.236068 +24 = 113 qo3qq4ox&#zc
where: c = sqrt(3)/2
...
hole
(o o4o subsym.) 		1 1/2 = 0.5 2 x o4o - line  
2 1/sqrt(2) = 0.707107 +4 = 6 xo ox4oo&#zc - squit
where: c = sqrt(3)/2
3 sqrt(5)/2 = 1.118034 +8 = 14 x q4o
4 sqrt(3/2) = 1.224745 +8 = 22 xu ox4qo&#zc
where: c = sqrt(3)/2
...

4D Lattice Center Number min. Radius Count of points Hull
C4 (primitive tessic)
unit = tesseract edge 		lattice point
(full o3o3o4o sym.) 		0 0 1 point
1 1 +8 = 9 q3o3o4o - hex
2 sqrt(2) = 1.414214 +24 = 33 o3q3o4o - ico
3 sqrt(3) = 1.732051 +32 = 65 o3o3q4o - rit
4 2 +24 = 89 o3u3o4o - ico
5 sqrt(5) = 2.236068 +48 = 137 oq3oq3oo4uo&#zh
6 sqrt(6) = 2.449490 +96 = 233 q3o3q4o - rico
... OEIS A046895  
hole
(full o3o3o4o sym.) 		1 1 16 o3o3o4x - tes
2 sqrt(3) = 1.732051 +64 = 80 q3o3o4x
3 sqrt(5) = 2.236068 +96 = 176 o3q3o4x
4 sqrt(7) = 2.645751 +128 = 304 Qo3oo3oq4xx&#zh
5 3 +208 = 512 oq3oq3oo4dx&#zh
...
D4 (alternated tessic)
unit = tesseract's square diagonal 		lattice point
(full o3o4o3o sym.) 		0 0 1 point
1 1 +24 = 25 x3o4o3o - ico
2 sqrt(2) = 1.414214 +24 = 49 o3o4o3q - (dual) ico
3 sqrt(3) = 1.732051 +96 = 145 o3x4o3o - rico
4 2 +24 = 169 u3o4o3o - ico
5 sqrt(5) = 2.236068 +144 = 313 x3o4o3q
6 sqrt(6) = 2.449490 +96 = 409 o3o4q3o - (other) rico
... OEIS A046949  
hole
(o3o3o4o subsym.) 		1 1/sqrt(2) = 0.707107 8 x3o3o4o - hex
2 sqrt(3/2) = 1.224745 +32 = 40 o3o3x4o - rit
3 sqrt(5/2) = 1.581139 +48 = 88 x3x3o4o - thex
4 sqrt(7/2) = 1.870829 +128 = 216 1/q-scaled oq3oo3qo4xu&#zx
5 3/sqrt(2) = 2.121320 +104 = 320 do3ox3ox4oo&#zh
...
A4 (cyclo pennic)
unit = pentachoron edge 		lattice point
(double o3o3o3o sym.) 		0 0 1 point
1 1 +20 = 21 x3o3o3x - spid
2 sqrt(2) = 1.414214 +30 = 51 o3x3x3o - deca
3 sqrt(3) = 1.732051 +60 = 111 uo3ox3xo3ou&#zq
4 2 +60 = 171 xuo3uoo3oou3oux&#z(qqh)
...
deep hole
(single o3o3o3o sym.) 		1 sqrt(3/5) = 0.774597 10 o3x3o3o - rap
2 sqrt(8/5) = 1.264911 +20 = 30 o3o3x3x - tip
3 sqrt(13/5) = 1.612452 +60 = 90 x3x3o3x - prip
...
shallow hole
(single o3o3o3o sym.) 		1 sqrt(2/5) = 0.632456 5 x3o3o3o - pen
2 sqrt(7/5) = 1.183216 +30 = 35 o3x3o3x - srip
...

© 2004-2024
top of page