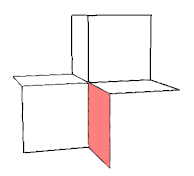
The Voronoi complex and the Delone complex of the primitive cubic lattice are relatively shifted copies of this cubic honeycomb.
The cubes of this honeycomb could be alternatedly rejected, then re-connected by means of squats instead;
this is what cuhsquah would be.
This honeycomb can be considered as the inifinite blend (or stack) of a single monostratic slab thereof, which is squattip.
A facial subset, built from the lacing squares of the 4-prismatic cells of x4o3o4x each, such that just 6 of those
squares remain at each vertex, by itself describes the regular infinite skew polyhedron x4o6o|4,
a modwrap of the hyperbolical tiling x4o6o.
Incidence matrix according to Dynkin symbol
x4o3o4o (N → ∞)
. . . . | N ♦ 6 | 12 | 8
--------+---+----+----+--
x . . . | 2 | 3N | 4 | 4
--------+---+----+----+--
x4o . . | 4 | 4 | 3N | 2
--------+---+----+----+--
x4o3o . ♦ 8 | 12 | 6 | N
snubbed forms: s4o3o4o
x4o3o4x (N → ∞)
. . . . | 8N ♦ 3 3 | 3 6 3 | 1 3 3 1
--------+----+---------+-----------+----------
x . . . | 2 | 12N * | 2 2 0 | 1 2 1 0
. . . x | 2 | * 12N | 0 2 2 | 0 1 2 1
--------+----+---------+-----------+----------
x4o . . | 4 | 4 0 | 6N * * | 1 1 0 0
x . . x | 4 | 2 2 | * 12N * | 0 1 1 0
. . o4x | 4 | 0 4 | * * 6N | 0 0 1 1
--------+----+---------+-----------+----------
x4o3o . ♦ 8 | 12 0 | 6 0 0 | N * * *
x4o . x ♦ 8 | 8 4 | 2 4 0 | * 3N * *
x . o4x ♦ 8 | 4 8 | 0 4 2 | * * 3N *
. o3o4x ♦ 8 | 0 12 | 0 0 6 | * * * N
snubbed forms: s4o3o4x, s4o3o4s, s4o3o4s'
o3o3o *b4x (N → ∞)
. . . . | 2N ♦ 6 | 12 | 4 4
-----------+----+----+----+----
. . . x | 2 | 6N | 4 | 2 2
-----------+----+----+----+----
. o . *b4x | 4 | 4 | 6N | 1 1
-----------+----+----+----+----
o3o . *b4x ♦ 8 | 12 | 6 | N *
. o3o *b4x ♦ 8 | 12 | 6 | * N
snubbed forms: o3o3o *b4s
x4o3o4/3o (N → ∞)
. . . . | N ♦ 6 | 12 | 8
----------+---+----+----+--
x . . . | 2 | 3N | 4 | 4
----------+---+----+----+--
x4o . . | 4 | 4 | 3N | 2
----------+---+----+----+--
x4o3o . ♦ 8 | 12 | 6 | N
o4o3o4/3x (N → ∞)
. . . . | N ♦ 6 | 12 | 8
----------+---+----+----+--
. . . x | 2 | 3N | 4 | 4
----------+---+----+----+--
. . o4/3x | 4 | 4 | 3N | 2
----------+---+----+----+--
. o3o4/3x ♦ 8 | 12 | 6 | N
x4o3o4/3x (N → ∞)
. . . . | 8N ♦ 3 3 | 3 6 3 | 1 3 3 1
----------+----+---------+-----------+----------
x . . . | 2 | 12N * | 2 2 0 | 1 2 1 0
. . . x | 2 | * 12N | 0 2 2 | 0 1 2 1
----------+----+---------+-----------+----------
x4o . . | 4 | 4 0 | 6N * * | 1 1 0 0
x . . x | 4 | 2 2 | * 12N * | 0 1 1 0
. . o4/3x | 4 | 0 4 | * * 6N | 0 0 1 1
----------+----+---------+-----------+----------
x4o3o . ♦ 8 | 12 0 | 6 0 0 | N * * *
x4o . x ♦ 8 | 8 4 | 2 4 0 | * 3N * *
x . o4/3x ♦ 8 | 4 8 | 0 4 2 | * * 3N *
. o3o4/3x ♦ 8 | 0 12 | 0 0 6 | * * * N
x4/3o3o4/3o (N → ∞)
. . . . | N ♦ 6 | 12 | 8
------------+---+----+----+--
x . . . | 2 | 3N | 4 | 4
------------+---+----+----+--
x4/3o . . | 4 | 4 | 3N | 2
------------+---+----+----+--
x4/3o3o . ♦ 8 | 12 | 6 | N
x4/3o3o4/3x (N → ∞)
. . . . | 8N ♦ 3 3 | 3 6 3 | 1 3 3 1
------------+----+---------+-----------+----------
x . . . | 2 | 12N * | 2 2 0 | 1 2 1 0
. . . x | 2 | * 12N | 0 2 2 | 0 1 2 1
------------+----+---------+-----------+----------
x4/3o . . | 4 | 4 0 | 6N * * | 1 1 0 0
x . . x | 4 | 2 2 | * 12N * | 0 1 1 0
. . o4/3x | 4 | 0 4 | * * 6N | 0 0 1 1
------------+----+---------+-----------+----------
x4/3o3o . ♦ 8 | 12 0 | 6 0 0 | N * * *
x4/3o . x ♦ 8 | 8 4 | 2 4 0 | * 3N * *
x . o4/3x ♦ 8 | 4 8 | 0 4 2 | * * 3N *
. o3o4/3x ♦ 8 | 0 12 | 0 0 6 | * * * N
o3o3o *b4/3x (N → ∞)
. . . . | 2N ♦ 6 | 12 | 4 4
-------------+----+----+----+----
. . . x | 2 | 6N | 4 | 2 2
-------------+----+----+----+----
. o . *b4/3x | 4 | 4 | 6N | 1 1
-------------+----+----+----+----
o3o . *b4/3x ♦ 8 | 12 | 6 | N *
. o3o *b4/3x ♦ 8 | 12 | 6 | * N
snubbed forms: o3o3o *b4s
((x∞o)) ((x4o4o)) (N → ∞)
. . . . . | N ♦ 2 4 | 8 4 | 8
----------+---+------+------+--
x . . . . | 2 | N * | 4 0 | 4
. . x . . | 2 | * 2N | 2 2 | 4
----------+---+------+------+--
x . x . . | 4 | 2 2 | 2N * | 2
. . x4o . | 4 | 0 4 | * N | 2
----------+---+------+------+--
x . x4o . ♦ 8 | 4 8 | 4 2 | N
snubbed forms: ((s∞o))2((s4o4o))
((x∞o)) ((o4x4o)) (N → ∞)
. . . . . | 2N ♦ 2 4 | 8 2 2 | 4 4
----------+----+-------+--------+----
x . . . . | 2 | 2N * | 4 0 0 | 2 2
. . . x . | 2 | * 4N | 2 1 1 | 2 2
----------+----+-------+--------+----
x . . x . | 4 | 2 2 | 4N * * | 1 1
. . o4x . | 4 | 0 4 | * N * | 2 0
. . . x4o | 4 | 0 4 | * * N | 0 2
----------+----+-------+--------+----
x . o4x . ♦ 8 | 4 8 | 4 2 0 | N *
x . . x4o ♦ 8 | 4 8 | 4 0 2 | * N
snubbed forms: ((s∞o))2((o4s4o))
((x∞o)) ((x4o4x)) (N → ∞)
. . . . . | 4N ♦ 2 2 2 | 4 4 1 2 1 | 2 4 2
----------+----+----------+--------------+-------
x . . . . | 2 | 4N * * | 2 2 0 0 0 | 1 2 1
. . x . . | 2 | * 4N * | 2 0 1 1 0 | 2 2 0
. . . . x | 2 | * * 4N | 0 2 0 1 1 | 0 2 2
----------+----+----------+--------------+-------
x . x . . | 4 | 2 2 0 | 4N * * * * | 1 1 0
x . . . x | 4 | 2 0 2 | * 4N * * * | 0 1 1
. . x4o . | 4 | 0 4 0 | * * N * * | 2 0 0
. . x . x | 4 | 0 2 2 | * * * 2N * | 0 2 0
. . . o4x | 4 | 0 0 4 | * * * * N | 0 0 2
----------+----+----------+--------------+-------
x . x4o . ♦ 8 | 4 8 0 | 4 0 2 0 0 | N * *
x . x . x ♦ 8 | 4 4 4 | 2 2 0 2 0 | * 2N *
x . . o4x ♦ 8 | 4 0 8 | 0 4 0 0 2 | * * N
snubbed forms: ((s∞o))2((s4o4x))
((x∞x)) ((x4o4o)) (N → ∞)
. . . . . | 2N ♦ 1 1 4 | 4 4 4 | 4 4
----------+----+--------+----------+----
x . . . . | 2 | N * * | 4 0 0 | 4 0
. x . . . | 2 | * N * | 4 0 0 | 0 4
. . x . . | 2 | * * 4N | 1 1 2 | 2 2
----------+----+--------+----------+----
x . x . . | 4 | 2 0 2 | 2N * * | 2 0
. x x . . | 4 | 0 2 2 | * 2N * | 0 2
. . x4o . | 4 | 0 0 4 | * * 2N | 1 1
----------+----+--------+----------+----
x . x4o . ♦ 8 | 4 0 8 | 4 0 2 | N
. x x4o . ♦ 8 | 0 4 8 | 0 4 2 | N
snubbed forms: ((s∞x))2((s4o4o))
((x∞x)) ((o4x4o)) (N → ∞)
. . . . . | 4N ♦ 1 1 4 | 4 4 2 2 | 2 2 2 2
----------+----+----------+-------------+--------
x . . . . | 2 | 2N * * | 4 0 0 0 | 2 2 0 0
. x . . . | 2 | * 2N * | 0 4 0 0 | 0 0 2 2
. . . x . | 2 | * * 8N | 1 1 1 1 | 1 1 1 1
----------+----+----------+-------------+--------
x . . x . | 4 | 2 0 2 | 4N * * * | 1 1 0 0
. x . x . | 4 | 0 2 2 | * 4N * * | 0 0 1 1
. . o4x . | 4 | 0 0 4 | * * 2N * | 1 0 1 0
. . . x4o | 4 | 0 0 4 | * * * 2N | 0 1 0 1
----------+----+----------+-------------+--------
x . o4x . ♦ 8 | 4 0 8 | 4 0 2 0 | N * * *
x . . x4o ♦ 8 | 4 0 8 | 4 0 0 2 | * N * *
. x o4x . ♦ 8 | 0 4 8 | 0 4 2 0 | * * N *
. x . x4o ♦ 8 | 0 4 8 | 0 4 0 2 | * * * N
snubbed forms: ((s∞x))2((o4s4o))
((x∞x)) ((x4o4x)) (N → ∞)
. . . . . | 8N ♦ 1 1 2 2 | 2 2 2 2 1 2 1 | 1 2 1 1 2 1
----------+----+-------------+----------------------+--------------
x . . . . | 2 | 4N * * * | 2 2 0 0 0 0 0 | 1 2 1 0 0 0
. x . . . | 2 | * 4N * * | 0 0 2 2 0 0 0 | 0 0 0 1 2 1
. . x . . | 2 | * * 8N * | 1 0 1 0 1 1 0 | 1 1 0 1 1 0
. . . . x | 2 | * * * 8N | 0 1 0 1 0 1 1 | 0 1 1 0 1 1
----------+----+-------------+----------------------+--------------
x . x . . | 4 | 2 0 2 0 | 4N * * * * * * | 1 1 0 0 0 0
x . . . x | 4 | 2 0 0 2 | * 4N * * * * * | 0 1 1 0 0 0
. x x . . | 4 | 0 2 2 0 | * * 4N * * * * | 0 0 0 1 1 0
. x . . x | 4 | 0 2 0 2 | * * * 4N * * * | 0 0 0 0 1 1
. . x4o . | 4 | 0 0 4 0 | * * * * 2N * * | 1 0 0 1 0 0
. . x . x | 4 | 0 0 2 2 | * * * * * 4N * | 0 1 0 0 1 0
. . . o4x | 4 | 0 0 0 4 | * * * * * * 2N | 0 0 1 0 0 1
----------+----+-------------+----------------------+--------------
x . x4o . ♦ 8 | 4 0 8 0 | 4 0 0 0 2 0 0 | N * * * * *
x . x . x ♦ 8 | 4 0 4 4 | 2 2 0 0 0 2 0 | * 2N * * * *
x . . o4x ♦ 8 | 4 0 0 8 | 0 4 0 0 0 0 2 | * * N * * *
. x x4o . ♦ 8 | 0 4 8 0 | 0 0 4 0 2 0 0 | * * * N * *
. x x . x ♦ 8 | 0 4 4 4 | 0 0 2 2 0 2 0 | * * * * 2N *
. x . o4x ♦ 8 | 0 4 0 8 | 0 0 0 4 0 0 2 | * * * * * N
((x∞o ((x∞o)) ((x∞o)) (N → ∞)
. . . . . . | N ♦ 2 2 2 | 4 4 4 | 8
------------+---+-------+-------+--
x . . . . . | 2 | N * * | 2 2 0 | 4
. . x . . . | 2 | * N * | 2 0 2 | 4
. . . . x . | 2 | * * N | 0 2 2 | 4
------------+---+-------+-------+--
x . x . . . | 4 | 2 2 0 | N * * | 2
x . . . x . | 4 | 2 0 2 | * N * | 2
. . x . x . | 4 | 0 2 2 | * * N | 2
------------+---+-------+-------+--
x . x . x . ♦ 8 | 4 4 4 | 2 2 2 | N
((x∞x)) ((x∞o)) ((x∞o)) (N → ∞)
. . . . . . | 2N ♦ 1 1 2 2 | 2 2 2 2 4 | 4 4
------------+----+-----------+------------+----
x . . . . . | 2 | N * * * | 2 2 0 0 0 | 4 0
. x . . . . | 2 | * N * * | 0 0 2 2 0 | 0 4
. . x . . . | 2 | * * 2N * | 1 0 1 0 2 | 2 2
. . . . x . | 2 | * * * 2N | 0 1 0 1 2 | 2 2
------------+----+-----------+------------+----
x . x . . . | 4 | 2 0 2 0 | N * * * * | 2 0
x . . . x . | 4 | 2 0 0 2 | * N * * * | 2 0
. x x . . . | 4 | 0 2 2 0 | * * N * * | 0 2
. x . . x . | 4 | 0 2 0 2 | * * * N * | 0 2
. . x . x . | 4 | 0 0 2 2 | * * * * 2N | 1 1
------------+----+-----------+------------+----
x . x . x . ♦ 8 | 4 0 4 4 | 2 2 0 0 2 | N *
. x x . x . ♦ 8 | 0 4 4 4 | 0 0 2 2 2 | * N
((x∞x)) ((x∞x)) ((x∞o)) (N → ∞)
. . . . . . | 4N ♦ 1 1 1 1 2 | 1 1 2 1 1 2 2 2 | 2 2 2 2
------------+----+----------------+---------------------+--------
x . . . . . | 2 | 2N * * * * | 1 1 2 0 0 0 0 0 | 2 2 0 0
. x . . . . | 2 | * 2N * * * | 0 0 0 1 1 2 0 0 | 0 0 2 2
. . x . . . | 2 | * * 2N * * | 1 0 0 1 0 0 2 0 | 2 0 2 0
. . . x . . | 2 | * * * 2N * | 0 1 0 0 1 0 0 2 | 0 2 0 2
. . . . x . | 2 | * * * * 4N | 0 0 1 0 0 1 1 1 | 1 1 1 1
------------+----+----------------+---------------------+--------
x . x . . . | 4 | 2 0 2 0 0 | N * * * * * * * | 2 0 0 0
x . . x . . | 4 | 2 0 0 2 0 | * N * * * * * * | 0 2 0 0
x . . . x . | 4 | 2 0 0 0 2 | * * 2N * * * * * | 1 1 0 0
. x x . . . | 4 | 0 2 2 0 0 | * * * N * * * * | 0 0 2 0
. x . x . . | 4 | 0 2 0 2 0 | * * * * N * * * | 0 0 0 2
. x . . x . | 4 | 0 2 0 0 2 | * * * * * 2N * * | 0 0 1 1
. . x . x . | 4 | 0 0 2 0 2 | * * * * * * 2N * | 1 0 1 0
. . . x x . | 4 | 0 0 0 2 2 | * * * * * * * 2N | 0 1 0 1
------------+----+----------------+---------------------+--------
x . x . x . ♦ 8 | 4 0 4 0 4 | 2 0 2 0 0 0 2 0 | N * * *
x . . x x . ♦ 8 | 4 0 0 4 4 | 0 2 2 0 0 0 0 2 | * N * *
. x x . x . ♦ 8 | 0 4 4 0 4 | 0 0 0 2 0 2 2 0 | * * N *
. x . x x . ♦ 8 | 0 4 0 4 4 | 0 0 0 0 2 2 0 2 | * * * N
((x∞x)) ((x∞x)) ((x∞x)) (N → ∞)
. . . . . . | 8N ♦ 1 1 1 1 1 1 | 1 1 1 1 1 1 1 1 1 1 1 1 | 1 1 1 1 1 1 1 1
------------+----+-------------------+-------------------------------------+----------------
x . . . . . | 2 | 4N * * * * * | 1 1 1 1 0 0 0 0 0 0 0 0 | 1 1 1 1 0 0 0 0
. x . . . . | 2 | * 4N * * * * | 0 0 0 0 1 1 1 1 0 0 0 0 | 0 0 0 0 1 1 1 1
. . x . . . | 2 | * * 4N * * * | 1 0 0 0 1 0 0 0 1 1 0 0 | 1 1 0 0 1 1 0 0
. . . x . . | 2 | * * * 4N * * | 0 1 0 0 0 1 0 0 0 0 1 1 | 0 0 1 1 0 0 1 1
. . . . x . | 2 | * * * * 4N * | 0 0 1 0 0 0 1 0 1 0 1 0 | 1 0 1 0 1 0 1 0
. . . . . x | 2 | * * * * * 4N | 0 0 0 1 0 0 0 1 0 1 0 1 | 0 1 0 1 0 1 0 1
------------+----+-------------------+-------------------------------------+----------------
x . x . . . | 4 | 2 0 2 0 0 0 | 2N * * * * * * * * * * * | 1 1 0 0 0 0 0 0
x . . x . . | 4 | 2 0 0 2 0 0 | * 2N * * * * * * * * * * | 0 0 1 1 0 0 0 0
x . . . x . | 4 | 2 0 0 0 2 0 | * * 2N * * * * * * * * * | 1 0 1 0 0 0 0 0
x . . . . x | 4 | 2 0 0 0 0 2 | * * * 2N * * * * * * * * | 0 1 0 1 0 0 0 0
. x x . . . | 4 | 0 2 2 0 0 0 | * * * * 2N * * * * * * * | 0 0 0 0 1 1 0 0
. x . x . . | 4 | 0 2 0 2 0 0 | * * * * * 2N * * * * * * | 0 0 0 0 0 0 1 1
. x . . x . | 4 | 0 2 0 0 2 0 | * * * * * * 2N * * * * * | 0 0 0 0 1 0 1 0
. x . . . x | 4 | 0 2 0 0 0 2 | * * * * * * * 2N * * * * | 0 0 0 0 0 1 0 1
. . x . x . | 4 | 0 0 2 0 2 0 | * * * * * * * * 2N * * * | 1 0 0 0 1 0 0 0
. . x . . x | 4 | 0 0 2 0 0 2 | * * * * * * * * * 2N * * | 0 1 0 0 0 1 0 0
. . . x x . | 4 | 0 0 0 2 2 0 | * * * * * * * * * * 2N * | 0 0 1 0 0 0 1 0
. . . x . x | 4 | 0 0 0 2 0 2 | * * * * * * * * * * * 2N | 0 0 0 1 0 0 0 1
------------+----+-------------------+-------------------------------------+----------------
x . x . x . ♦ 8 | 4 0 4 0 4 0 | 2 0 2 0 0 0 0 0 2 0 0 0 | N * * * * * * *
x . x . . x ♦ 8 | 4 0 4 0 0 4 | 2 0 0 2 0 0 0 0 0 2 0 0 | * N * * * * * *
x . . x x . ♦ 8 | 4 0 0 4 4 0 | 0 2 2 0 0 0 0 0 0 0 2 0 | * * N * * * * *
x . . x . x ♦ 8 | 4 0 0 4 0 4 | 0 2 0 2 0 0 0 0 0 0 0 2 | * * * N * * * *
. x x . x . ♦ 8 | 0 4 4 0 4 0 | 0 0 0 0 2 0 2 0 2 0 0 0 | * * * * N * * *
. x x . . x ♦ 8 | 0 4 4 0 0 4 | 0 0 0 0 2 0 0 2 0 2 0 0 | * * * * * N * *
. x . x x . ♦ 8 | 0 4 0 4 4 0 | 0 0 0 0 0 2 2 0 0 0 2 0 | * * * * * * N *
. x . x . x ♦ 8 | 0 4 0 4 0 4 | 0 0 0 0 0 2 0 2 0 0 0 2 | * * * * * * * N
((qo3oo3oq3oo3*a))&#zx (N → ∞) → height = 0
(tegum sum of 2 alternate q-octets)
o.3o.3o.3o.3*a | N * ♦ 6 | 12 | 4 4
.o3.o3.o3.o3*a | * N ♦ 6 | 12 | 4 4
-------------------+-----+----+----+----
oo3oo3oo3oo3*a&#x | 1 1 | 6N | 4 | 2 2
-------------------+-----+----+----+----
qo .. oq .. &#zx | 2 2 | 4 | 6N | 1 1
-------------------+-----+----+----+----
qo3oo3oq .. &#x ♦ 4 4 | 12 | 6 | N *
qo .. oq3oo3*a&#x ♦ 4 4 | 12 | 6 | * N
reflecting the known fact that the primitive cubic lattice is the sum of 2 alternate fcc lattices
respectively that the fcc lattice is nothing but the alternation of the primitive cubic one
:x:4:o:4:o:&##x (N → ∞) → height = 1
o 4 o 4 o | N ♦ 4 2 | 4 8 | 8
---------------+---+------+------+--
x . . | 2 | 2N * | 2 2 | 4
:o:4:o:4:o:&#x | 2 | * N | 0 4 | 4
---------------+---+------+------+--
x 4 o . | 4 | 4 0 | N * | 2
:x: . . &#x | 4 | 2 2 | * 2N | 2
---------------+---+------+------+--
:x:4:o: . &#x ♦ 8 | 8 4 | 2 4 | N
:qoo:3:oqo:3:ooq:3*a&##xt (N → ∞) → all heights = 1/sqrt(3) = 0.577350
o.. 3 o.. 3 o.. 3*a | N * * ♦ 3 0 3 | 3 6 3 | 3 3 2
.o. 3 .o. 3 .o. 3*a | * N * ♦ 3 3 0 | 6 3 3 | 3 2 3
..o 3 ..o 3 ..o 3*a | * * N ♦ 0 3 3 | 3 3 6 | 2 3 3
-------------------------+-------+----------+----------+------
oo. 3 oo. 3 oo. 3*a&#x | 1 1 0 | 3N * * | 2 2 0 | 2 1 1
.oo 3 .oo 3 .oo 3*a&#x | 0 1 1 | * 3N * | 2 0 2 | 1 1 2
:o.o:3:o.o:3:o.o:3*a&#x | 1 0 1 | * * 3N | 0 2 2 | 1 2 1
-------------------------+-------+----------+----------+------
... oqo ... &#xt | 1 2 1 | 2 2 0 | 3N * * | 1 0 1
:qoo: ... ... &#xt | 2 1 1 | 2 0 2 | * 3N * | 1 1 0
... ... :ooq: &#xt | 1 1 2 | 0 2 2 | * * 3N | 0 1 1
-------------------------+-------+----------+----------+------
:qoo:3:oqo: ... &#xt ♦ 3 3 2 | 6 3 3 | 3 3 0 | N * *
:qoo: ... :ooq:3*a&#xt ♦ 3 2 3 | 3 3 6 | 0 3 3 | * N *
... :oqo:3:ooq: &#xt ♦ 2 3 3 | 3 6 3 | 3 0 3 | * * N
©
©