Acronym	rad (old: rhode)
Name	rhombic dodecahedron, granatahedron, Voronoi cell of face-centered cubic (fcc) lattice, terminally chamfered cube, terminally chamfered octahedron, surtegmated cube, surtegmated octahedron, Waterman polyhedron number 4 wrt. primitive cubic lattice C3 centered at a lattice point, Waterman polyhedron number 2 (and 6) wrt. body-centered cubic lattice C3* centered at a lattice point
	© ©
Inradius	sqrt(2/3) = 0.816497
Vertex figure	[r4], [R3]
Coordinates	(1, 1, 1)/sqrt(3)     & all permutations, all changes of sign (3-fold vertices, inscribed sqrt(4/3)-cube) (2, 0, 0)/sqrt(3)     & all permutations, all changes of sign (4-fold vertices, inscribed sqrt(8/3)-oct)
General of army	(is itself convex)
Colonel of regiment	(is itself locally convex)
Dual	co
Dihedral angles (at margins)	between {(r,R)2} and {(r,R)2}:   120°
Face vector	14, 24, 12
Confer	related polyhedra: chamfered cube   chamfered oct   general polytopal classes: Catalan polyhedra
External links

  ©    ©

The rhombs {(r,R)²} have vertex angles r = arccos(1/3) = 70.528779° resp. R = arccos(-1/3) = 109.471221°. Esp. rr : RR = sqrt(2). – Both, the actual shape of the rhombs and the dihedral angle given above, can easily be obtained from the Voronoi complex of the fcc honeycomb, radh, and its relation to the vertex-inscribed primitive cubic honeycomb chon, cf. also the right first 2 pictures. In fact, this relation to the fcc honeycomb, esp. its dual Delone complex, which here is just octet, readily shows how those above given numbers r and R come up: they are just the dihedral angles of tet and oct respectively.

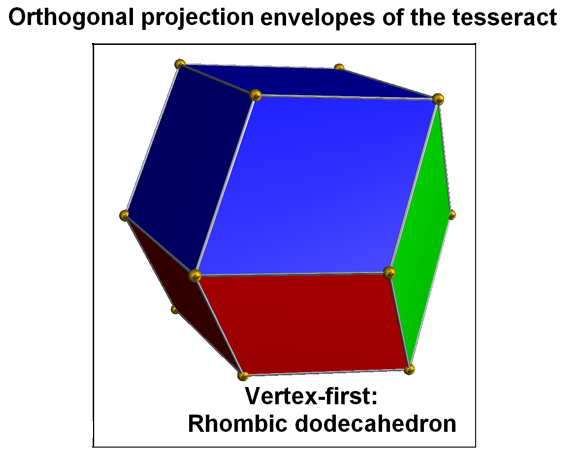
The last right picture displays that the vertex-first projection of the tes happens to be nothing but rad. In fact, there are exactly two ways of dissecting rad into four congruent rhombohedra, giving a total of eight possible rhombohedra, each a projected cube. The remaining 2 vertices of tes, which are not visible at the surface of rad, thereby get both projected to its body-center. These two rhombohedral dissections then just represent nothing but the front and back cover of the projection pre-image, i.e. of tes. – Thus, re-refering to the previous paragraph, radh happens to be nothing but a single sheet of cover from a likewise projection of test.

All a = rr and b = RR edges, as provided in the below description, only qualify as pseudo edges wrt. the full polyhedron. The true edge size used here is rR = x = 1.

By the very definition of Waterman polyhedra, not necessarily all vertices are on the same sphere. In here the 6 maximal ones (4-fold vertices) have a circumradius of 2/sqrt(3) = 1.154701, while the other 8 vertices (3-fold ones) only are at an radius of 1. Note that these numbers also coincide with the distances b = RR and x = rR respectively.

Being the dual of co and considering that one's coordinates, it is apparent that this solid is nothing but a ball wrt. the norm max(|x|+|y|, |x|+|z|, |y|+|z|).

Incidence matrix according to Dynkin symbol

o3m4o =
ao3oo4ob&#zx   → height = 0
                 a = rr = sqrt(8/3) = 1.632993
                 b = RR = 2/sqrt(3) = 1.154701

o.3o.4o.     | 6 * |  4 |  4  [r4]
.o3.o4.o     | * 8 |  3 |  3  [R3]
-------------+-----+----+---
oo3oo4oo&#x  | 1 1 | 24 |  2
-------------+-----+----+---
ao .. ob&#zx | 2 2 |  4 | 12  {(r,R)2}

m3o3m =
aoo3oao3ooa&#zx   → height = 0
                    a = rr = sqrt(8/3) = 1.632993

o..3o..3o..     | 4 * * |  3  0 |  3  [R3]
.o.3.o.3.o.     | * 6 * |  2  2 |  4  [r4]
..o3..o3..o     | * * 4 |  0  3 |  3  [R3]
----------------+-------+-------+---
oo.3oo.3oo.&#x  | 1 1 0 | 12  * |  2
.oo3.oo3.oo&#x  | 0 1 1 |  * 12 |  2
----------------+-------+-------+---
... oao ...&#xt | 1 2 1 |  2  2 | 12  {(r,R)2}