|
Acronym
|
...
|
|
Name
|
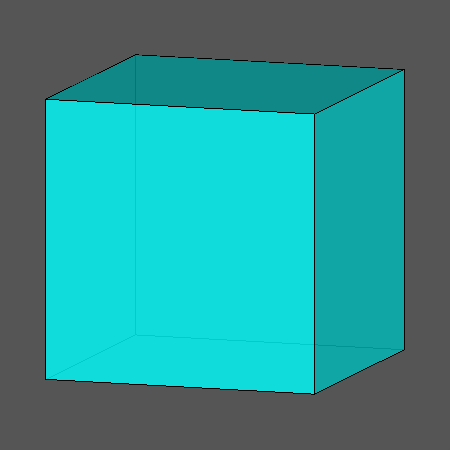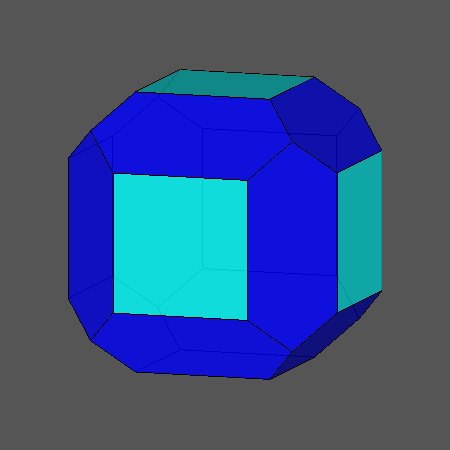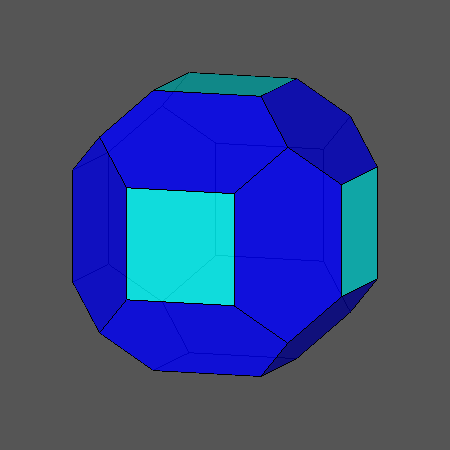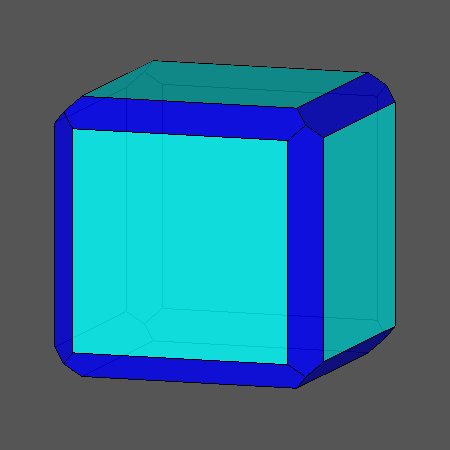
Waterman polyhedron number 5 wrt. body-centered cubic lattice C3* centered at a lattice point,
slightly chamfered cube,
octahedrally shallow truncated rhombic dodecahedron
|
|
|
 © ©
|
|
VRML
|
⭳
|
|
Vertex figure
|
[4,H2], [h3]
|
|
Coordinates
|
-
(1, 1, 1) & all changes of sign
(vertex inscribed cube)
-
(1/2, 1/2, 3/2) & all permutations, all changes of sign
|
|
General of army
|
(is itself convex)
|
|
Colonel of regiment
|
(is itself locally convex)
|
Dihedral angles
(at margins)
|
- between {4} and {(h,H,H)2}: 135°
- between {(h,H,H)2} and {(h,H,H)2}: 120°
|
|
Face vector
|
32, 48, 18
|
|
Confer
|
rad
cube
chic
|
The non-regular hexagons {(h,H,H)2} have vertex angles h = arccos(-1/3) = 109.471221° resp. H = arccos[-1/sqrt(3)] = 125.264390°.
Octahedral truncation applies to the octahedral vertices (vertex inscribed oct) only. Wrt. the rad this
produces new square faces there. These are then face planes of a cutting cube. –
The above transition shows a dynamical mutual scaling of cube and rad.
The chamfered cube (chic) then would be the instance, where all edges happen to have the same length.
However this Waterman polyhedron occurs at a slightly shallower depth.
(Note that here the diagonals of the non-regular hexagons will be side-parallel, while there they are not.)
Chamfering (or edge-only beveling – here is being applied to the cube) flatens the former edges into new
(non-regular hexagonal) faces.
There is a deeper, terminal chamfering of the cube too, which then reduces the original faces to nothing.
Then the hexagons will become rhombs and the total figure becomes the rad.
Incidence matrix according to Dynkin symbol
oq3oo4ux&#zc → height = 0
c = sqrt(3)/2 = 0.866025
both q and u are pseudo
(tegum sum of u-cube and (q,x)-sirco)
o.3o.4o. | 8 * | 3 0 | 3 0 [h3]
.o3.o4.o | * 24 | 1 2 | 2 1 [4,H2]
-------------+------+-------+-----
oo3oo4oo&#c | 1 1 | 24 * | 2 0 c
.. .. .x | 0 2 | * 24 | 1 1 x
-------------+------+-------+-----
oq .. ux&#zc | 2 4 | 4 2 | 12 * {(h,H,H)2}
.. .o4.x | 0 4 | 0 4 | * 6 {4}
©