| Site Map | Polytopes | Dynkin Diagrams | Vertex Figures, etc. | Incidence Matrices | Index |
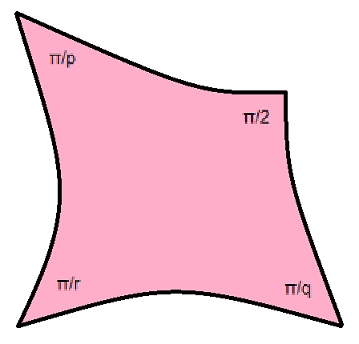
There is a further main issue to be regarded within hyperbolic geometry: In hyperbolic geometry even the compact fundamental domains are no longer restricted to simplices. Such more general fundamental domain polytopes commonly are called Coxeter domains (or: Coxeter polytopes), at least if those are elementary (i.e. the produced symmetry is convex). Accordingly, the dihedral angles (of the pairs of facets Fi and Fj) of Coxeter polytopes are bound to be ≤ π/2 (convexity), and those submultiplicative numbers (to π) have to be integral (finite order, elementary domain).
The other way round the known main results here state that any such polytope, with dihedral angles αi,j ≤ π/2, must be simple, i.e. its vertex figures remain simplicial. That any such polytope furthermore, provided its αi,j are of the form π / mi,j with integral mi,j, does generate a Coxeter group which acts properly on this space by means of reflections at its facets. Thereby that given polytope then will be its fundamental domain. And the entries of the Coxeter matrix (mi,j)i,j of this group are derivable as follows:
mi,j = 1 , if i = j ; else: mi,j = π / αi,j , if Fi ∩ Fj ≠ Ø mi,j = ∞ , if Fi ∩ Fj = Ø
Sure, the set of such polytopes is infinite. Even its classification is a still on-going task.
---- 2D More general Tilings (up) ----
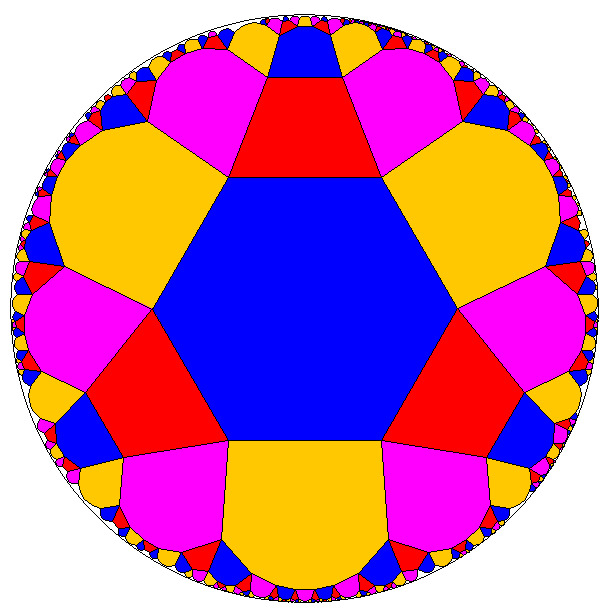
The picture shows an example of such a more general uniform hyperbolic tiling with a tetragonal domain: there are squares, hexagons, octagons, and decagons around any vertex.
In fact, in 2D we have this general theorem (the proof of which directly emanates from the provided example):
Usual Dynkin diagrams for such more general hyperbolics are clearly not defined, neither for the symmetry groups themselves, nor for the therefrom derived tesselations. Moreover, as the Wythoff kaleidoscopic construction essentially is based on those diagrams (resp. on the information decoded therein), this "more general case" thus also could be classically considered non-Wythoffian.
In view of the above cited theorem however, one might extend that diagrammal description by using a virtual simplex description, i.e. the number of nodes being again the number of facets of the (Coxeter) domain (which are orthogonal to the edges of the "omnitruncated" version), and the links are marked according to those mi,j (i≠j) whenever such domain facets intersect. Additionally we introduce a non-adjacency symbol: Ø whenever that pair of mirrors is defined by a pair of non-adjacent facets of the fundamental domain (which therefore won't intersect – within the reach of that domain, at least).
E.g. the according diagram of the above provided picture then can be given as x3xØx4xØ*a5*c (*b2*d). (In fact, the nodes at positions b,a,c,d in this sequence cyclically provide the sides of the fundamental tetragon, or equivalently the orthogonal edges of the tiling incident to an arbitrary vertex. And the links provide the spanned faces: hexagon (mb,a = 3), decagon (ma,c = 5), octagon (mc,d = 4), and (closing back) square (md,b = 2). I.e. node a represents the mirrors midway orthogonal to the hexagon/decagon edges, b correspondingly to the square/hexagon edges, c to the octagon/decagon edges, and d to the square/octagon edges. – But neither the domain sides b and c nor the sides a and d are adjacent. Accordingly there are no tiles (polygons) to be spanned by those pairs of mirrors (mb,c = md,a = Ø). At most they could be seen as pseudo bollogons, i.e. not really contained, faceting apeirogons with hyperbolic curvature.
As the number of facets of Coxeter domains exceeds those of simplices, the number of nodes in the symbol would be accordingly larger. Especially the usual relation, that the number of nodes equals 1 plus the dimension of the tesselation space (resp. of the embedded manifold), no longer holds in this generalization.
The symbol Ø in here was introduced ad hoc. Accordingly its usage clearly was designed by the current needs. Nonetheless there can be provided an according consistent complete theory (given below at 3D)!
| some considered 2D tilings ... | ||||
|---|---|---|---|---|
|
Coxeter domain |
|
|
|
|
|
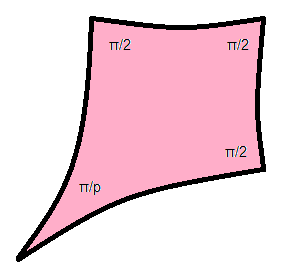
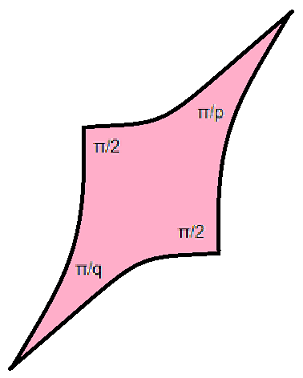
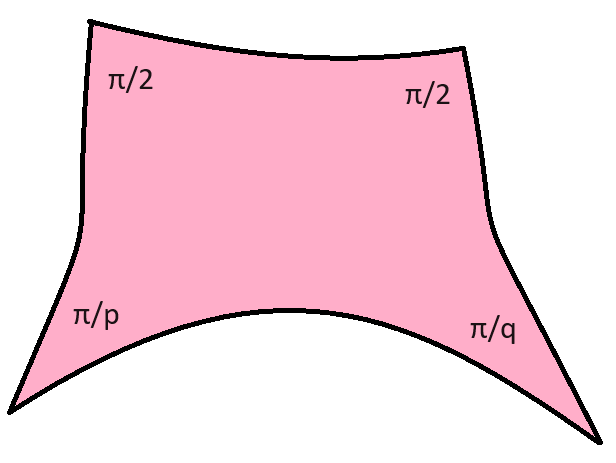
Dynkin diagram |
o o
| |
Ø | | Ø
| |
o-------o
P
|
P
o-------o
| |
Ø | | Ø
| |
o-------o
Q
|
o
|
Ø |
|
o
/ \
P / \ Q
/ Ø \
o-------o
|
o
/ \
P / Ø
/ R \
o-------o
\ /
Ø / Q
\ /
o
|
|
linearised symbol |
oØoPoØo |
oPoØoQoØ*a |
oØoPoØoQ*b |
oPoØoQoØ*aR*c |
| tilings |
xØx3xØx xØo3oØx xØx4xØx xØo4oØx xØoPoØx xØo∞oØx xØx∞xØx |
x3xØo3oØ*a x3oØx3oØ*a x3xØx3oØ*a x3xØx3xØ*a |
xØx3xØx3*b sØs3sØsQ*b |
x3xØx4xØ*a5*c o3xØx4xØ*a5*c o3xØo4xØ*a5*c s3sØs4sØ*a5*c x3xØx∞xØ*a3*c |
Note that the statement of the theorem could be read also such that those links with Ø symbols always need to have at least one adjacent node be ringed (i.e. using the x node symbol). This is essentially different to the ∞ symbol, which clearly might have both link ends un-ringed (i.e. using o node symbols – as far as no other restrictions would ask for those, for instance that each disconnected subgraph must use at least one non-o node). A further difference clearly is, that Ø never provides a polygonal element, whereas ∞ surely does (because it just can be considered as the limiting case of limn→∞ n-gon); either directly (if having an adjacent x), or else as vertex figure elemnent. (It was E. Vinberg who explicitly considered groups with ∞ usage.) An examplifying hyperbolic tiling, whos corresponding extended Dynkin diagram shows up this different usage most drastically, is xØo∞oØx. – Note on the other hand that the euclidean tiling x∞o x∞o would likewise not use those azes. Still the usage of the ∞ sign is not wrong there! The non-occurance there would be simply a mere consequence of the honeycomb product, represented by that disconnected graph.
For hyperbolic fundamental triangles, the size of sides is already fixed by the choice of the angles. But this does not hold true for other fundamental domains. In fact, for a fundamental n-gon there are n-3 degrees of freedom, usable for alterable side lengths. – This is just the same as for the single such reflection group of euclidean space: the one with a rectangular fundamental domain, where alike the relative scale of side length of the rectangular domain can be varied.
Recently some more general researches brought up hyperbolic tilings, which even exceed the preconditions of the above theorem. E.g. the completely independent and fully general elaboration of the bounds onto the numbers a and b for tilings of type [a,a,a,b]. It results in up to 4 different tilings (depending on the choice of those values a and b)!
---- 3D More general Honeycombs (up) ----
Just some examplifying 3D Coxeter domain classes:
(The refered sections of the first two list items also is intended to serve as an entrance to the here needed more general theory about Dynkin diagrams.)
It might be mentioned here also that several cases above are no longer simple, i.e. those domains provide themselves vertex figures which are no longer simplicical.
The most natural extension of simplicial domains to more general Coxeter domains would be quite generally that of simplicial prismatic domains, i.e. within 3D of triangular prismatic domains. The very idea in here is about laminate honeycombs, as Miss Krieger would call them. This means, one has to look for a Wythoffian hypercompact honeycomb, i.e. still with a simplicial domain, but where one of its facets is a bollocell (hyperbolic tiling), which furthermore has the same curvature as the whole honeycomb. Then it becomes obvious, that this bollocell kind of acts like a hemifacet in spherical polytopes, that is, the remainder could be mirrored at that bollocell, and the bollocell itself thereby becomes a pseudofacet only. With respect to the domain this operation clearly means, that one common intersection vertex of the fundamental domain, i.e. the one which stood for the chosen bollocell of the former domain, and which, because of the same curvature assumption, would have been situated on the far-points-sphere, now gets chopped off and the remaining base part of that former simplex will get mirrored at that cutting.
A well-known example once has been provided by Miss Krieger already, the lamina-truncate( x4x3o8o ) = o8o3x4xØx4*c. Here the bollocell x3o8o indeed has the same curvature as the whole honeycomb x4x3o8o. That is the remainder, then a laminate only of tics, can be mirrored thereon, thus resulting within this lamina-truncate accordingly. Its resulting vertex figure here is oxo8ooo&#kt.
When it now comes to the corresponding extended Coxeter-Dynkin diagram representation, then one first has to note that these are a dual representation. I.e. each domain boundary (reflection mirror) gets represented in a node of the diagram. That is, a trigonal prismatic domain requires for a trigonal tegmatic (i.e. bipyramidal) diagram. Further, within the prism the base faces are the ones, which do not intersect. Accordingly within the diagram it is the two opposing tips, which have to be linked by the non-joiner symbol Ø. For a quite general simplicial diagram of a honeycomb oPoQoRoS*aT*c *bU*d (just its symmetry, without any markings applied) we thus result, if oPoQoT*a would become the mirroring pseudo facet, in the laminated honeycomb oPoQoRoS*aT*cRoS*a *dU*bU*eØ*d. I.e. two identical simplicial diagrams externally blended at the then pseudo facet, where the two then still free tips become linked by the non-joiner. A bit more general, if there are two such simplicial oPoQoRoS*aT*c *bU*d and oPoQoR'oS'*aT*c *bU'*d, both having some same "hemifacetal" bollocell oPoQoT*a, those could be used for alternating laminates within oPoQoRoS*aT*cR'oS'*a *dU*bU'*eØ*d.
The general question about possible facet subsymmetries for any of these simplicial prismatic domains is rather easy. These are represented by the facets of this tegum (i.e. bipyramid) shaped diagram, i.e. all of the former simplicial facets, except of the now equatorial pseudo one, which now got blended out. That one in turn can be characterized to contain none of the non-joiner adjoined nodes. I.e. worded differently: any new facet shall contain at least one of the non-joiner adjoined nodes. In fact, if it would contain both, then it must be (or contain) an aze element, running perpendicular to both (parallel) bases of the prismatic domain.
Also the question about their vertex figures can be given on a general level here. Obviously it turns out to be just the bipyramid on the vertex figure of that blended out bollocell.
o- -Ø- -o
\ /
p q
\ /
o
/ \
s r
/ \
o- -Ø- -o
To get an understanding what happens in case of more general 3D Coxeter domains, we consider now explicitly the general case of the to the right being shown symmetry, which has the linearised notation o-p-o-Ø-o-q-*a-r-o-Ø-o-s-*a. Note that the Dynkin diagram always displays the dual graph of the domain, i.e. the nodes represent the boundaries of the domain, the links of the diagram represent the ridges of the domain. Here the domain then represents either a one-ended, not necessarily straight rectangular beam or a (then bounded) pyramid: We have 5 faces of the domain, corresponding to the nodes of the graph. One face is connected to all the other ones by dihedral angles, which are represented by those numbers of the link marks p,q,r,s. The other, lateral faces of the domain are mutually either ridged by right angles (the 4 not represented links of this "complete pentagon", each originally corresponding to link marks which ought to be 2), or are not connected at all (opposing domain faces, represented in the graph by non-incidence symbols Ø). Whether the domain will be bounded (a rectangular pyramid) or unbounded (a true open beam) depends on the overall geometry provided by the parameters p,q,r,s. (This in fact is similar to the simplicial domains, which within hyperbolic geometry might have their tips well at infinity too. I.e. the tip of the "pyramid" here likewise might be finite or not.)
First of all we have to ask: what are the possible subsymmetries? – For simplicial domains the answer was easy: just omit any single node together with its incident links; the remainder diagram would represent the facet symmetry. Here we have to be a bit more careful! The facet symmetries of the to be derived polytopes clearly are that ones, which are provided by the vertex figures of the domain: Those vertex figures do intersect orthogonally with the ridges of the domain (i.e. with the intersections of domain boundaries), and therefore reduce to a similar problem in one dimension less. So, in our case of a rectangular pyramid, those are that of the tip (thus still omitting a single node: that one, which represents the base, i.e. the one with the 4 shown true emanating links), and any of the base corners, all resulting in triangles, which now each do omit more than just a single node! So we get in our example the subsymmetry o-Ø-o o-Ø-o (which happens to have euclidean curvature and therefore the ominous pseudo bollogons here become pseudo horogons, that is we could replace the Ø symbol here also by the ∞ symbol). Obviously the at the right displayed general symmetry therefore needs to be at least paracompact. The other subsymmetries here are given by o-p-o-r-o, o-q-o-s-o, o-q-o-r-o, and o-p-o-s-o (which, depending on the numbers p,q,r,s might make the total symmetry even a hypercompact one). – E.g. o-p-o-r-o is deduced as folows: at a bottom vertex of the domain we have 3 emanating ridges. Two of them run along the bottom rectangle and thus are defined by the angles represented by the corresponding link marks p and r. The third is the lacing ridge, with incident perpendicular boundaries, which corresponds to the respective omitted graph link.
Next we have to ask for possible decorations of such generalized Dynkin diagrams in the sense of a generalized Wythoff kaleidoscopical construction. For that purpose we will abandon uniformity restrictions for a moment and consider just the kaleidoscopical construction. This then might result in tiles with any edge lengths. Sure, the omnitruncation then always is possible, i.e. applying the x node symbol everywhere. (But we shall have in mind that these xs all might come out to be differently sized.) Whereas already in 2D we had seen, that not all applications of the o node symbols where allowed. – Considering first the vertex figure of the tip of the at the right displayed examplifying pyramidal domain. There we do know the answer already: this is because of o-Ø-o o-Ø-o = o-∞-o o-∞-o (as described above). Thus we are back to A1×A1 symmetry, i.e. a reducible symmetry group (with disconnected graph). There we have to use at least one x node per component. – And the rules of the theorem of 2D effectively likewise ask, that at least one end of those links, marked by Ø signs, have to bear an x decoration. In other words: at most one end may carry an o decoration!
In order to go even beyond this special case (of our example), we have once more to take refuge to the usual on/off explanation of the decorations for that purpose (of possible decorations). An x node is used in kaleidoscopical construction for a seed point lying off that special mirror plane, while an o node is used, if the seed point is incident to (i.e. on) the mirror. Therefore, the omnitruncate always has all nodes decorated by x nodes, because its seed point is placed completely within the domain, that is off from all mirrors. Next the seed point clearly can be placed for sure at the inner part of any of the bounding facets of the domain. Then it is simply on that specific mirror, but off from all others. This results in the decoration by a single o node. Further the seed point can be placed at the intersection of two neighbouring boundary facets, etc. just as for normal Dynkin diagrams. But obviously with respect to a pair of non-intersecting facets (of the domain boundary), it becomes obvious, that the seed point has to be off from the one, if it wants to be on the other. This is the intrinsic reason for the rule provided at the end of the former paragraph.
Still, there will be an exception to that rule, so. What about placing the seed point at the tip of our pyramidal domain of consideration? This is obviously an allowed position too. Then this seed point is nonetheless on all mirror planes of this domain vertex. That is, the subsymmetry diagram (i.e. restricted to the vertex figure of this vertex) thus has only o nodes, independent of therein contained Ø links.
If finally the question comes to the facets of a polytope with Coxeter domain, then those can be read from the generalized Dynkin diagram in the very same way now, as for non-generalized ones: they are the corresponding polytopes according to the provided decorated subgraphs, restricted as in the afore mentioned subsymmetries.
Accordingly the above provided general symmetry group type would allow (besides other locally finite solutions for p,q,r,s) e.g. for the hyperbolic honeycombs of the following table. – But it should be warned here, that not all choices of numbers for those parameters p,q,r,s would provide a locally finite honeycomb, i.e. one without producing a dense modul. Just as for all the non-generalzed Dynkin diagrams too, this issue not only has to be checked for all to be used subsymmetries individually, but once more for the to be combined (i.e. full) symmetry as well.
And now we have to come back to uniformity considerations. I.e. to the question whether all applied x nodes truely will represent edges of the tesselation with a single equal size. The answer to this question is highly depending to the actual form of the domain itself! For simplicial domains there have been always according positions of the seed point. But the larger domain facet amount of Coxeter domains provides more restrictions to be met simultanuously, which generally exceed the possible degrees of freedom of its positioning. So we have to be quite careful here. (Again: any position of the seed point does provide a hyperbolic tesselation for sure by means of kaleidoscopical construction. It just is the additional restriction to equal edge sizes only, which might become impossible!)
In the following table known uniforms are marked with °. (Others will still have to be checked!)
o- -Ø- -o
\ /
3 3
\ /
o
/ \
3 3
/ \
o- -Ø- -o
|
o- -Ø- -o
\ /
3 4
\ /
o
/ \
3 4
/ \
o- -Ø- -o
|
o- -Ø- -o
\ /
4 4
\ /
o
/ \
4 4
/ \
o- -Ø- -o
| |
o3oØo3*a3oØo3*a |
o3oØo4*a3oØo4*a |
o4oØo4*a4oØo4*a | ... |
|---|---|---|---|
x3oØo3*a3oØo3*a o3xØo3*a3xØo3*a x3xØo3*a3xØo3*a o3xØx3*a3xØo3*a x3xØx3*a3xØo3*a o3xØx3*a3xØx3*a x3xØx3*a3xØx3*a ° |
x3oØo4*a3oØo4*a o3xØo4*a3xØo4*a ° o3xØo4*a3oØx4*a o3oØx4*a3oØx4*a ° x3xØo4*a3xØo4*a x3xØo4*a3oØx4*a x3oØx4*a3oØx4*a o3xØx4*a3xØo4*a o3xØx4*a3oØx4*a x3xØx4*a3xØo4*a x3xØx4*a3oØx4*a o3xØx4*a3xØx4*a x3xØx4*a3xØx4*a |
x4oØo4*a4oØo4*a ° o4xØo4*a4xØo4*a ° x4xØo4*a4xØo4*a o4xØx4*a4xØo4*a x4xØx4*a4xØo4*a o4xØx4*a4xØx4*a ° x4xØx4*a4xØx4*a ° |
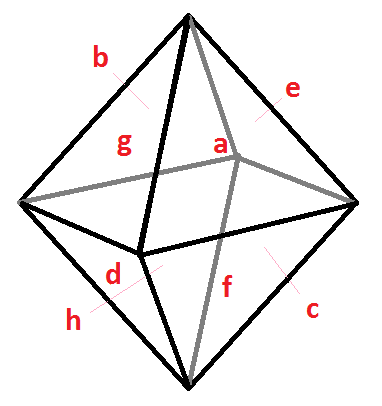
Next we turn to an octahedral Coxeter domain. The derived techniques do work right the same. Just the number of links between the nodes (incident ones -p- plus non-incident ones -Ø-) here increases and the linearised version of the (generalised) Dynkin symbol becomes a lot harder to decipher.
Thus we like to restrict our consideration here to the symmetry example with all incident link marks being 2 (hyperbolic right-angled octahedral domain) – although this is debted only for representational reasons: Thus we have to display within our symbol the pairs of non-connected domain faces only, all other links can then be dropped in the graph. The hyperbolic honeycomb of all repeated fundamental domains itself then will be described by x3o4o4o, resp. each fundamental domain by any of its cells.
Using the mirror- (i.e. node)-order provided in the right picture, this symmetry could be represented by the following generalised Dynkin symbol (underneath the real nodes, for easier reading purposes, the order character is provided additionally, to which the virtuals do refer):
oØoØoØoØoØoØoØoØ*aØ*cØ*gØ*eØ*hØ*fØ*bØ*dØ*a a b c d e f g h
Here then follow the posible members of this symmetry. Remind the general rule, that at most one end of an Ø link is allowed to have an o node. (Again it is just a matter of the high number of such links, which makes this enumeration tedious.) And again add the single exception from that rule, provided above. The outcome then looks surprising small with respect to the number of (real) nodes involved. In fact, by domain symmetry there are exactly four possibilities: the seed point being at a vertex (e.g. the top one), at an edge (e.g. the one between "a" and "e"), at a face (e.g. at "a"), resp. within the body of the domain.
In the following table known uniforms are marked with °. (Others will still have to be checked!)
oØoØoØoØoØoØoØoØ*aØ*cØ*gØ*eØ*hØ*fØ*bØ*dØ*a |
|---|
oØoØxØxØoØxØoØxØ*aØ*cØ*gØ*eØ*hØ*fØ*bØ*dØ*a ° oØxØxØxØoØxØxØxØ*aØ*cØ*gØ*eØ*hØ*fØ*bØ*dØ*a oØxØxØxØxØxØxØxØ*aØ*cØ*gØ*eØ*hØ*fØ*bØ*dØ*a xØxØxØxØxØxØxØxØ*aØ*cØ*gØ*eØ*hØ*fØ*bØ*dØ*a ° |
Here we have a domain with 6 boundaries, opposite pairs of which are not coincident, i.e. bear the Ø-mark.
The easiest example then would be, if all remaining boundary connections would be 2. But then the symbol decomposes just into oØo oØo oØo – which happens to become euclidean and thus could be rewritten into o∞o o∞o o∞o. Any decoration here would just result in chon.
A further, still partially orthogonal example would result, when we apply non-orthogonal dihedral boundary angles only onto the Petrie polygon of this domain. Then the domain could be linearized into opoqorosotou*aØ*d *bØ*e *cØ*f. The easiest examples of that class are contained in the next table. (Note that at any Ø-link we always need at least one node being ringed!)
In the following tables known uniforms are marked with °. (Others will still have to be checked!)
| (same as before, just that the equatorial zig-zag has alternating link marks) | ||||||
o3o3o3o3o3o3*aØ*d *bØ*e *cØ*f |
o3o4o3o4o3o4*aØ*d *bØ*e *cØ*f |
o3o5o3o5o3o5*aØ*d *bØ*e *cØ*f | ... | ||||
|---|---|---|---|---|---|---|---|
x3o3x3o3x3o3*aØ*d *bØ*e *cØ*f ° x3x3x3o3o3o3*aØ*d *bØ*e *cØ*f x3x3x3x3o3o3*aØ*d *bØ*e *cØ*f x3x3x3o3x3o3*aØ*d *bØ*e *cØ*f x3x3x3x3x3o3*aØ*d *bØ*e *cØ*f x3x3x3x3x3x3*aØ*d *bØ*e *cØ*f ° |
x3o4x3o4x3o4*aØ*d *bØ*e *cØ*f ° x3x4x3o4o3o4*aØ*d *bØ*e *cØ*f x3x4x3x4o3o4*aØ*d *bØ*e *cØ*f x3x4x3o4x3o4*aØ*d *bØ*e *cØ*f x3x4x3x4x3o4*aØ*d *bØ*e *cØ*f x3x4x3x4x3x4*aØ*d *bØ*e *cØ*f ° |
x3o5x3o5x3o5*aØ*d *bØ*e *cØ*f ° x3x5x3o5o3o5*aØ*d *bØ*e *cØ*f x3x5x3x5o3o5*aØ*d *bØ*e *cØ*f x3x5x3o5x3o5*aØ*d *bØ*e *cØ*f x3x5x3x5x3o5*aØ*d *bØ*e *cØ*f x3x5x3x5x3x5*aØ*d *bØ*e *cØ*f ° | |||||
Applying thereas all links of the full octahedral Dynkin graph with equal link marks (now larger 2) results in the following table.
o3o3o3o3o3o3*aØ*d *b3*d3*f3*bØ*e *c3*e3*a3*cØ*f | ... |
|---|---|
x3o3x3o3x3o3*aØ*d *b3*d3*f3*bØ*e *c3*e3*a3*cØ*f ° x3x3x3o3o3o3*aØ*d *b3*d3*f3*bØ*e *c3*e3*a3*cØ*f ° x3x3x3x3o3o3*aØ*d *b3*d3*f3*bØ*e *c3*e3*a3*cØ*f x3x3x3o3x3o3*aØ*d *b3*d3*f3*bØ*e *c3*e3*a3*cØ*f x3x3x3x3x3o3*aØ*d *b3*d3*f3*bØ*e *c3*e3*a3*cØ*f x3x3x3x3x3x3*aØ*d *b3*d3*f3*bØ*e *c3*e3*a3*cØ*f |
© 2004-2024 | top of page |
