Hyperbolic Tesselations
Some Hyperbolic Tiling Classes with Specific Local Configuration Types
M. Čtrnáct provided a full research, which uniform tilings of several given vertex configuration types would be possible
in general. This research thereby is completely independent of any whatsoever expanded usage of Dynkin symbols and also of the given
theorem provided in the context of Coxeter domains. In fact, it exceeds the reach of both realms.
He starts his research not directly with the mere vertex configuration, but rather with edge configurations. He uses capital letters for
some given tile, and lower case letters for the directly or diametrally adjacent ones. In the considered quest we get the following 6 edge
configurations. The code provided beside each configuration refers
by : to its label,
by ⇅ to its opposite configuration (the configuration having the edge-opposite tile capitalised,
in fact a 180° rotation around the respective edge center),
by ↶ to the set of possible edge configurations at the next edge of the main tile towards its left,
by ↷ to the set of possible edge configurations at the next edge of the main tile towards its right.
(These and several more similar research results originally were posted
here.)
Which uniform tilings of vertex type [a3,b] = [a,a,a,b] are possible in general?
The local edge configurations then are
a | b | a
--+---+--
a | A | a :A ⇅E ↶D,B1 ↷D,B2
b | a | a
--+---+--
a | A | b :B1 ⇅B1 ↶C,B2 ↷A
b | a | b
--+---+--
a | A | a :C ⇅D ↶C,B2 ↷C,B1
a | a | a
--+---+--
b | A | b :D ⇅C ↶A ↷A
a | a | b
--+---+--
b | A | a :B2 ⇅B2 ↶A ↷C,B1
a | a | a
--+---+--
a | B | a :E ⇅A ↶E ↷E
The first 5 configurations describe the possible edges of an A-gon. B-gons do have just a single edge type, because they have to be surrounded
completely by a-gons.
The next step then is to build (larger) vertex configurations: now not by means of mere incident tiles, rather by means of these just
deduced incident edge configurations. By definition one has a b-gon incident to each vertex. And the edge configuration type here is E
(with the edge-opposite configuration A). Thus we have to start with E|A, will have to consider the sequences ↷,
and finally will end in A|E. The possible sequences here are:
E|A ↷ D|C ↷ C|D ↷ A|E
E|A ↷ D|C ↷ B1|B1 ↷ A|E
E|A ↷ B2|B2 ↷ C|D ↷ A|E
E|A ↷ B2|B2 ↷ B1|B1 ↷ A|E
Or in terms of tile configurations these codings correspond respectively to the types:
a | a
--+--
a | B | A | b
--+---+---+--
a | A | A | a
--+--
b | a E|A ↷ D|C ↷ C|D ↷ A|E
a | a
--+--
a | B | A | b
--+---+---+--
a | A | A | a
--+--
a | b E|A ↷ D|C ↷ B1|B1 ↷ A|E
a | a
--+--
a | B | A | a
--+---+---+--
a | A | A | b
--+--
b | a E|A ↷ B2|B2 ↷ C|D ↷ A|E
a | a
--+--
a | B | A | a
--+---+---+--
a | A | A | b
--+--
a | b E|A ↷ B2|B2 ↷ B1|B1 ↷ A|E
Here the first and last larger vertex configuration are 2 different symmetrical ones, while the others just form a single enantiomorph pair.
Thus those 2 middle ones ought to be grouped.
Finally one considers the possible sequences of edge configurations around the tiles themselves.
Here the (above grouped) larger vertex configurations already have to be considered independently.
It shall be noted that the consecutive edge configurations around any tile always are given in parts by the respective substrings
|x ↷ y|.
-
Thus in the first case we get for tile(s) a just the unconnectable sequences A↷D↷A and
C↷C, and for tile b just E↷E. Therefore we will have a colorable tiling with
tiles a1 = ADAD..., a2 = CCCC..., and
b = EEE....
Esp. the number of sides of the tiles a has to be even.
Here tile b always is adjoined to tile a1
and separated from tile a2. The latter is just diametrally incident at the corners.
And, conversely, a1 adjoins to some b at every
alternate side. Whereas a2 is completely surrounded by
a1 type tiles.
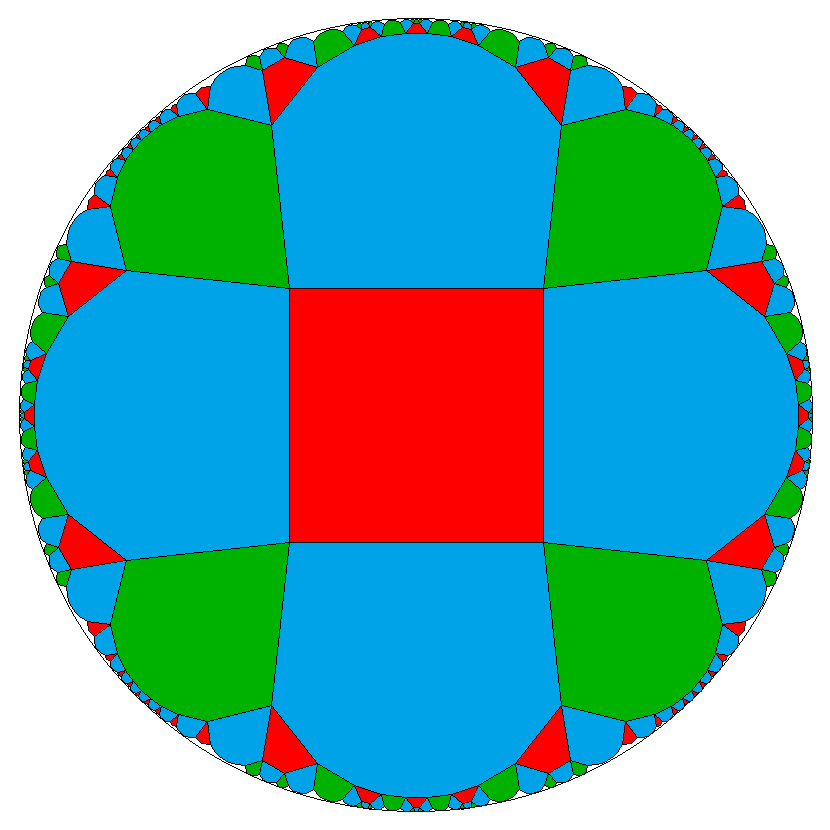
–
This case in general is nothing but the Wythoffian tiling x-a/2-x-a-o-b-*a.
In fact the tiles x-a/2-x . here are
a1, the tiles . x-a-o are
a2, and x . o-b-*a are b.
Btw. the "/2" here might cancel out a posteriori with the two marked nodes on either side, but this is not even be asked for, as we assumed
a to be even and therefore that division generally can take place already before the decoration is being applied.
-
For the middle group we get for tile(s) a either the pure sequences A↷D↷A and
A↷B2↷C↷B1↷A, or we get the mixed sequence
A↷D↷A↷B2↷C↷B1↷A.
For tile b again just E↷E.
Within the first sub-case we have again a colorable tiling with tiles a1 = ADAD... and
a2 = AB2CB1... (periodically each).
Here the number of sides of the tiles a thus has to be divisible by 4.
But a1 adjoins to b = EEE... at every
alternate side, while a2 adjoins to it at every fouth side only.
Further the tile b will be adjacent to both tiles a1
and a2 alternatingly (as those both do use the edge type A).
Therefore the number of sides of tile b has to be even here!
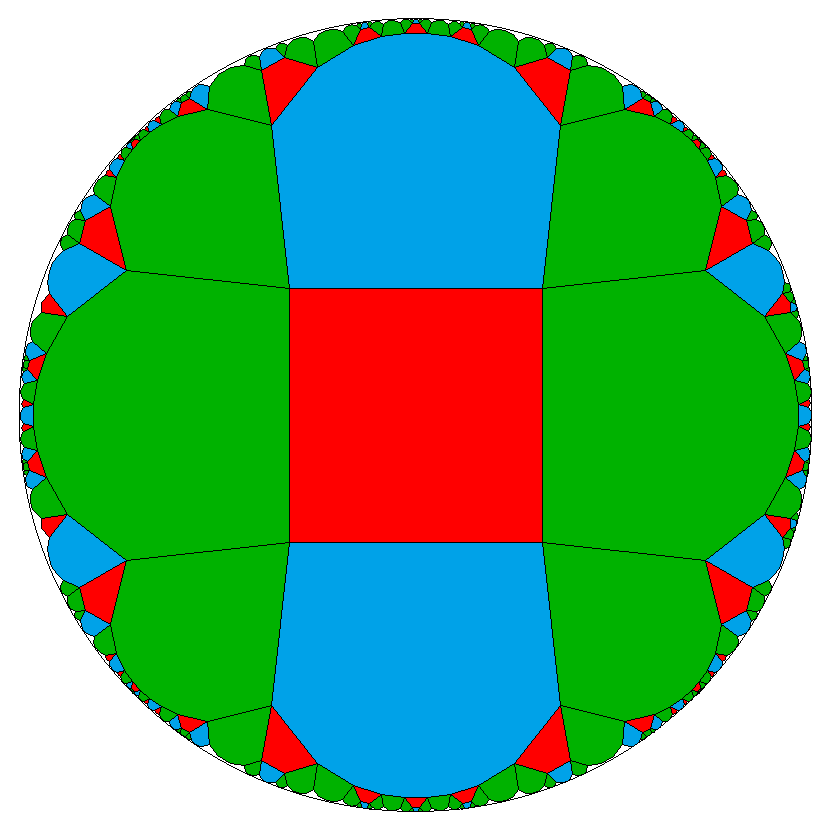
-
Within the other sub-case we just have a single tile a = ADAB2CB1...
(periodically).
It therefore has a number of sides, which is divisible by 6. And again some tile b = EEE....
There is no possible coloring (while keeping uniformity) for the a tiles here.
And also no restriction on tile b.
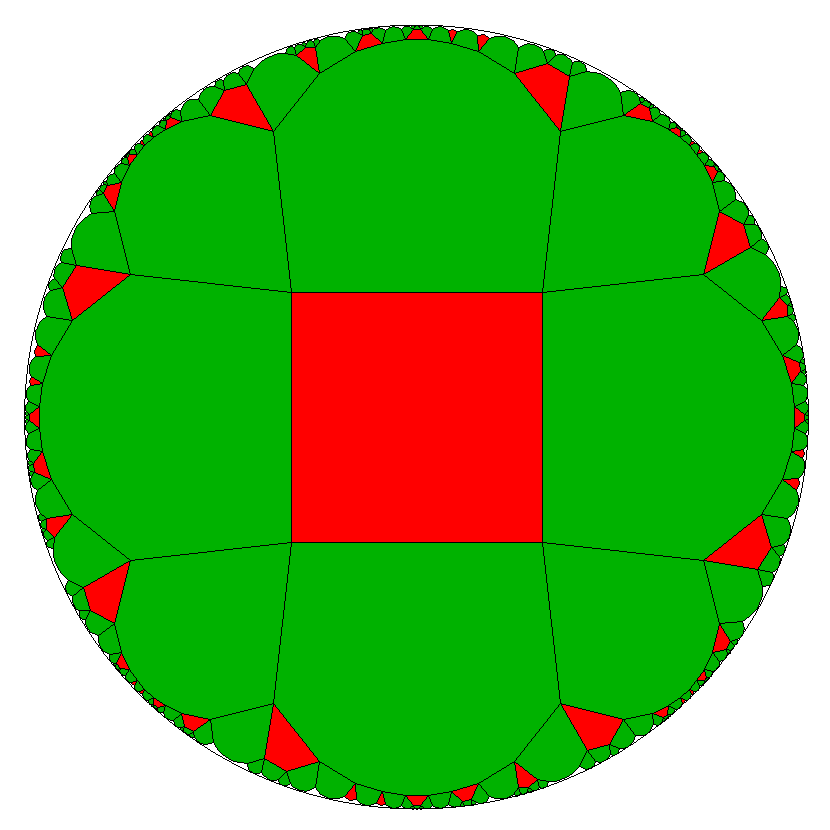
-
Finally in the last case we get for tile a simply the sequence A↷B2↷B1↷A
and for tile b once more just E↷E.
This results in a tiling with tile a = AB2B1...
(periodically). It therefore has a number of sides, which is divisible by 3.
Only every third side of a adjoins to some b = EEE....
At the vertex inbetween, the tile b then would be diametrally opposite.
And again no restriction onto tile b.
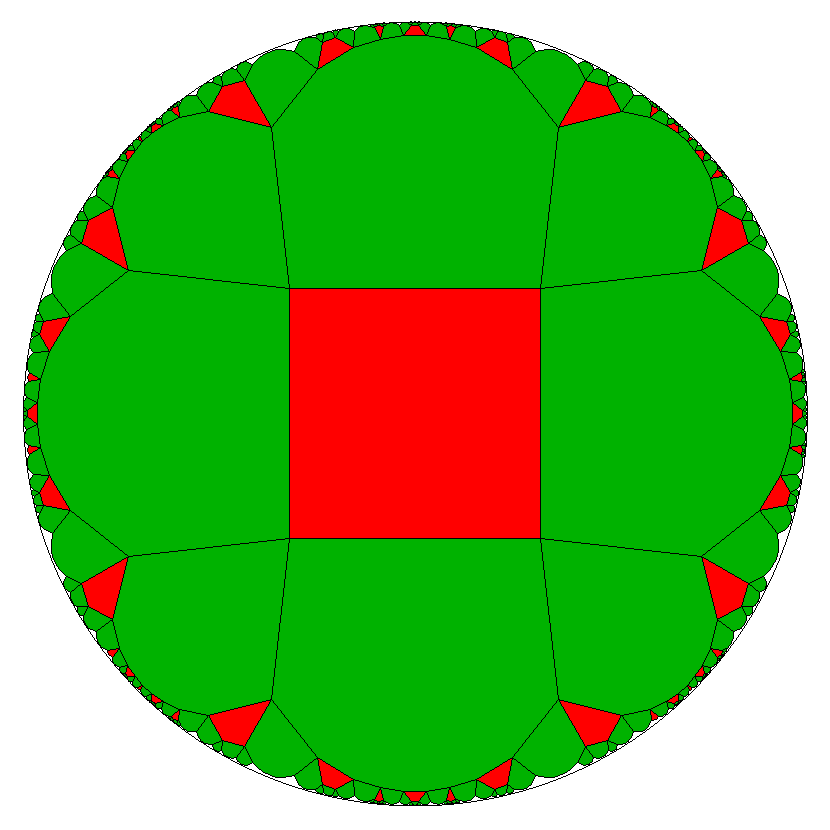
–
The most simple example here clearly would be a = {3} and b = {n} for any n≥2. This then becomes finite and is
nothing but the n-gonal antiprism.
And even more general, any such tiling, as described in this case here, allows for
some vertex coloring according to a Grünbaumian multi-wrap around such an antiprism, or then even results by the according mod-wrap
identification of like-colored vertices (and incident edges too) in just that antiprism.
– This relation to the antiprism moreover shows, that any such tiling here allows for a 2-coloring of both, the a-tiles and the b-tiles:
Just distinguish between the pre-images of the top-polygon and the bottom-polygon, resp. between the pre-images of those
Grünbaumian multi-wraps, which result in bottom-based lateral triangles, and those of the top-based ones.
But thereby the uniformity of the tiling also would be lost, because the pre-images of the top-vertices and those of the bottom-vertices
then would be distinguished too.
The pair of lowest numbers, which allows for all 4 cases, i.e. bows to all divisibility constraints simultanuously,
thus would be a = {12} and b = {4}. That choice therefore is depicted above each.
[3,9,9,9] e.g. on the other hand would be unique, it can exist only as type 4.
Moreover it is a quite evident example for not matching the requirements of
the above mentioned theorem, because here all tiles are odd.
Conversely, putting together all these cases in an alternative way, we just get the restriction, that a needs to be divisable
either by 2 or by 3 at least. E.g. a can neither be {5}, {7}, {11} etc. when required to become an
[a,a,a,b] tiling.
Which uniform tilings of vertex type [a4,b] = [a,a,a,a,b] are possible in general?
Right according the lines of the previous section this quest can be solved too. Starting with the here possible edge configurations:
a | b | a
a >+---+< a
a | A | a :A ⇅H ↶B1,E1,G ↷G,E2,B2
b | a | a
a >+---+< a
a | A | b :B1 ⇅B1 ↶C1,F,E2 ↷A
b | a | a
a >+---+< b
a | A | a :C1 ⇅E1 ↶C1,F,E2 ↷B1,C1,D
b | a | b
a >+---+< a
a | A | a :D ⇅G ↶C1,F,E2 ↷E1,F,C2
a | a | a
b >+---+< a
a | A | b :E1 ⇅C1 ↶D,C2,B2 ↷A
a | a | a
b >+---+< b
a | A | a :F ⇅F ↶D,C2,B2 ↷B1,C1,D
a | a | b
b >+---+< a
a | A | a :C2 ⇅E2 ↶D,C2,B2 ↷E1,F,C2
a | a | a
a >+---+< a
b | A | b :G ⇅D ↶A ↷A
a | a | a
a >+---+< b
b | A | a :E2 ⇅C2 ↶A ↷B1,C1,D
a | a | b
a >+---+< a
b | A | a :B2 ⇅B2 ↶A ↷E1,F,C2
a | a | a
a >+---+< a
a | B | a :H ⇅A ↶H ↷H
Next one builds (larger) vertex configurations, as deduced by these incident edge configurations.
The 27 possible sequences, grouped by mirror images, here are:
H|A ↷ G|D ↷ E1|C1 ↷ B1|B1 ↷ A|H
H|A ↷ B2|B2 ↷ C2|E2 ↷ D|G ↷ A|H †
H|A ↷ G|D ↷ E1|C1 ↷ C1|E1 ↷ A|H
H|A ↷ E2|C2 ↷ C2|E2 ↷ D|G ↷ A|H
H|A ↷ G|D ↷ E1|C1 ↷ D|G ↷ A|H
H|A ↷ G|D ↷ C2|E2 ↷ D|G ↷ A|H †
H|A ↷ G|D ↷ F|F ↷ B1|B1 ↷ A|H
H|A ↷ B2|B2 ↷ F|F ↷ D|G ↷ A|H
H|A ↷ G|D ↷ F|F ↷ C1|E1 ↷ A|H
H|A ↷ E2|C2 ↷ F|F ↷ D|G ↷ A|H †
H|A ↷ G|D ↷ F|F ↷ D|G ↷ A|H
H|A ↷ G|D ↷ C2|E2 ↷ B1|B1 ↷ A|H
H|A ↷ B2|B2 ↷ E1|C1 ↷ D|G ↷ A|H †
H|A ↷ G|D ↷ C2|E2 ↷ C1|E1 ↷ A|H
H|A ↷ E2|C2 ↷ E1|C1 ↷ D|G ↷ A|H
H|A ↷ E2|C2 ↷ E1|C1 ↷ B1|B1 ↷ A|H
H|A ↷ B2|B2 ↷ C2|E2 ↷ C1|E1 ↷ A|H
H|A ↷ E2|C2 ↷ E1|C1 ↷ C1|E1 ↷ A|H
H|A ↷ E2|C2 ↷ C2|E2 ↷ C1|E1 ↷ A|H †
H|A ↷ E2|C2 ↷ F|F ↷ B1|B1 ↷ A|H
H|A ↷ B2|B2 ↷ F|F ↷ C1|E1 ↷ A|H †
H|A ↷ E2|C2 ↷ F|F ↷ C1|E1 ↷ A|H †
H|A ↷ E2|C2 ↷ C2|E2 ↷ B1|B1 ↷ A|H
H|A ↷ B2|B2 ↷ E1|C1 ↷ C1|E1 ↷ A|H
H|A ↷ B2|B2 ↷ E1|C1 ↷ B1|B1 ↷ A|H
H|A ↷ B2|B2 ↷ C2|E2 ↷ B1|B1 ↷ A|H †
H|A ↷ B2|B2 ↷ F|F ↷ B1|B1 ↷ A|H
Now we try to build up edge sequences from those contained |x ↷ y| for the tiles a and b.
Generally we restrict to uniform tilings only, therefore either a single such vertex configuration or at most the union with its
mirror image can be used. Sequences which do not close (corresponding groups are marked † above)
will have to be omitted in the following listing. This then results in the following possible cases:
-
The second one either allows for 2 pure sequences
a1 = AG...,
a2 = AE2DE1..., together with an enantiomorph pair of fully symmetrical tiles
a3 = C1...,
a4 = C2....
Thus all these a-gons have to be divisible by 4.
And tiles b = H... have to be even here, according to alternating adjoins of tiles a1 and a2.
[4,4,4,4,6]  , [8,8,8,8,4]
, [8,8,8,8,4]  , ...
, ...
-
Alternatively it also allows for the mixed sequence
a1 = AGAE2DE1..., also together with
a2 = C1...,
a3 = C2....
Then a-gons have to be divisible by 6 and tiles b = H... have no restriction here.
[6,6,6,6,3] 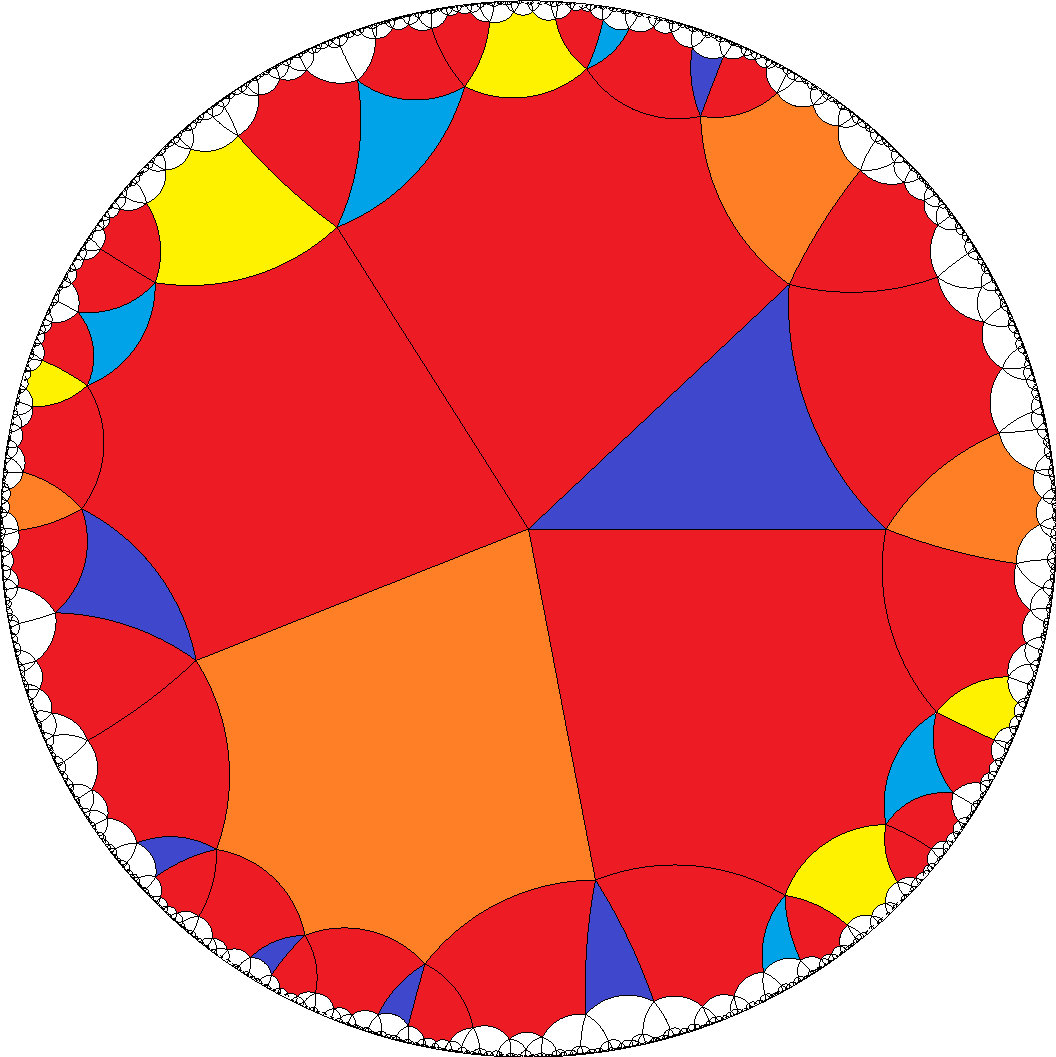 , [6,6,6,6,4]
, [6,6,6,6,4] 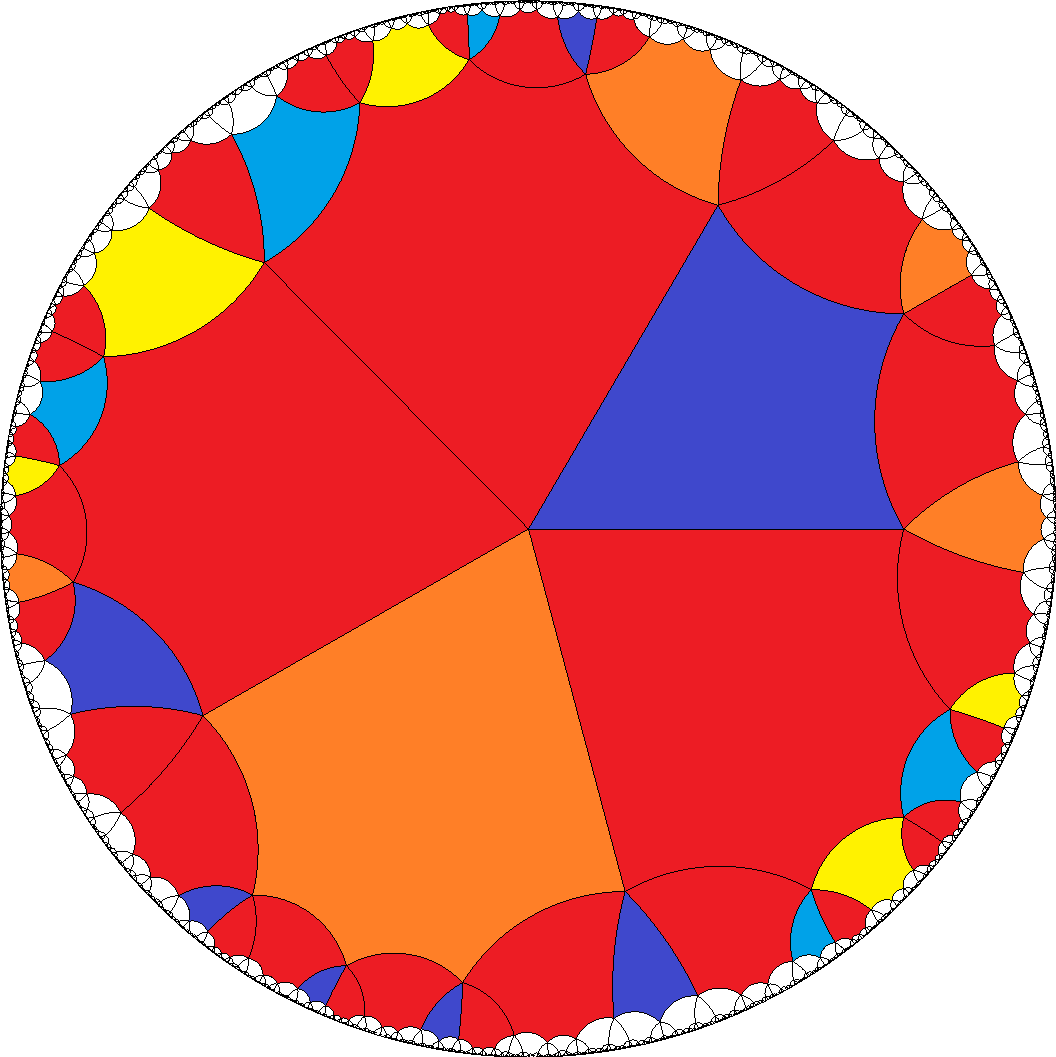 , ...
, ...
-
The fourth one also allows for 3 pure sequences
a1 = AG...,
a2 = AB2FB1..., and
a3 = DF....
Thus a-gons have to be divisible by 4.
And tiles b = H... have to be even here, according to alternating adjoins of tiles a1 and a2.
[4,4,4,4,6] 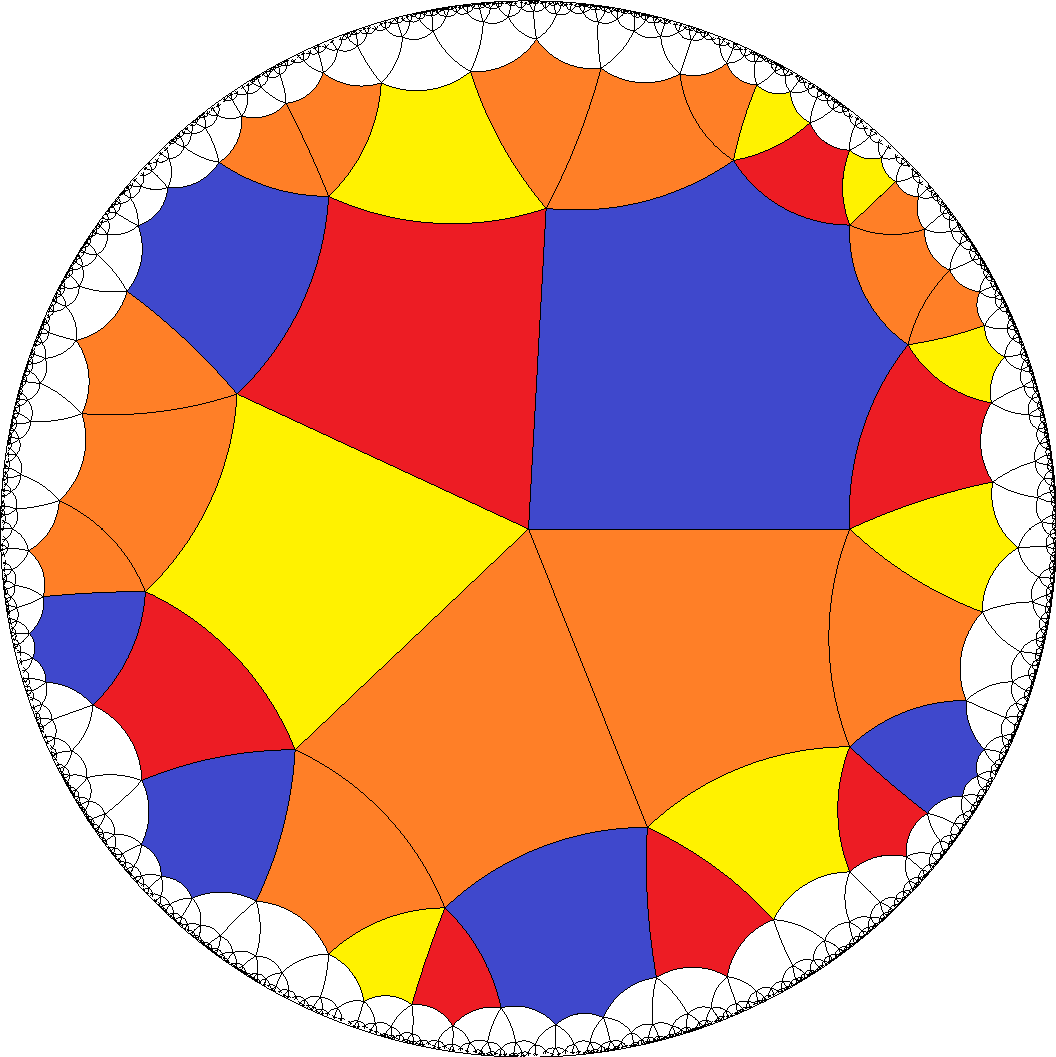 , [8,8,8,8,4]
, [8,8,8,8,4] 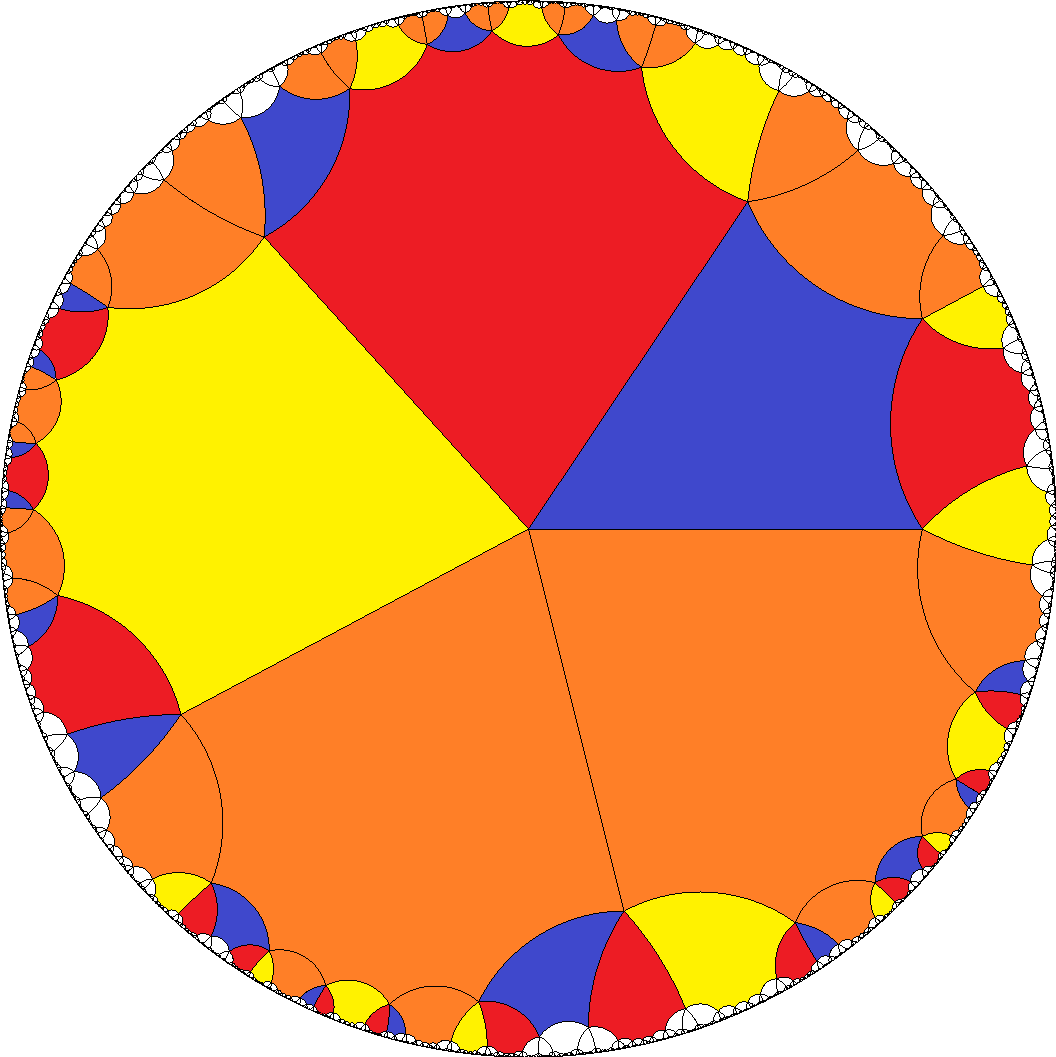 , ...
, ...
-
Alternatively it also allows for the one mixed and one pure sequence according to
a1 = AGAB2FB1... and
a2 = DF....
Then a-gons then have to be divisible by 6 and tiles b = H... have no restriction here.
[6,6,6,6,3] 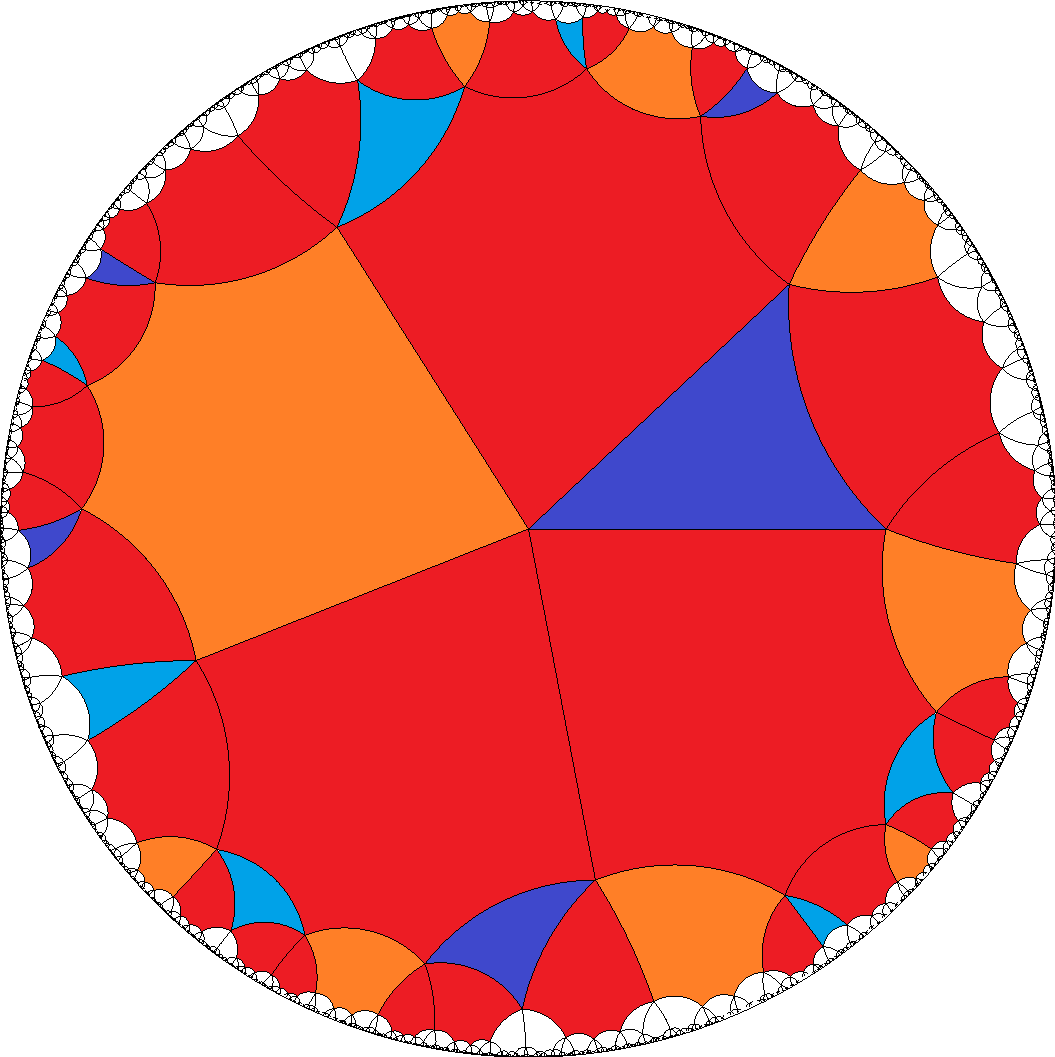 , [6,6,6,6,4]
, [6,6,6,6,4] 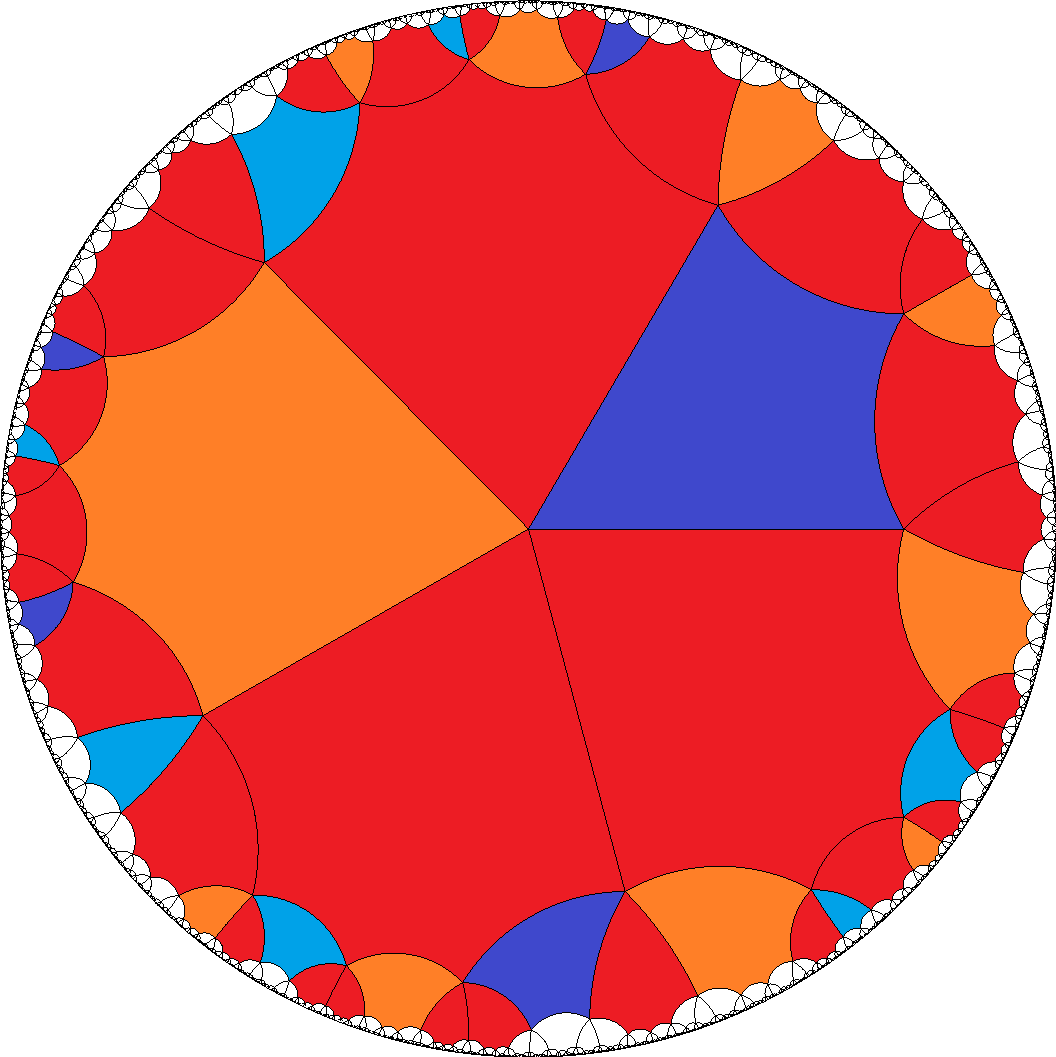 , ...
, ...
-
But there is a different such partially mixed case as well according to
a1 = AG... and
a2 = AB2FDFB1....
Then a-gons then have to be divisible by 6 and tiles b = H... have to be even again.
[6,6,6,6,4] 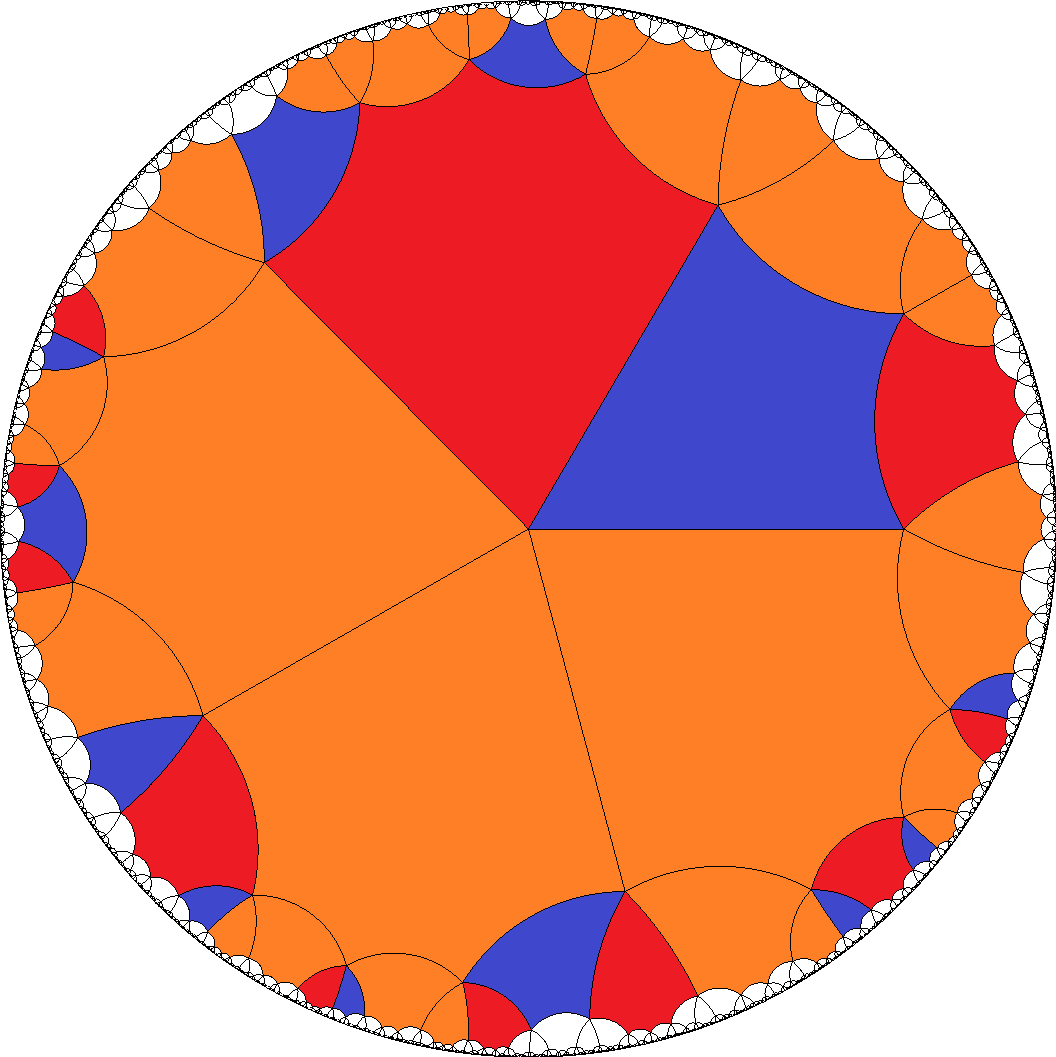 , ...
, ...
-
Finally this case also allows for the fully mixed sequence
a = AGAB2FDFB1..., which then has to be divisible by 8.
Tiles b = H... have no restriction here.
[8,8,8,8,4] 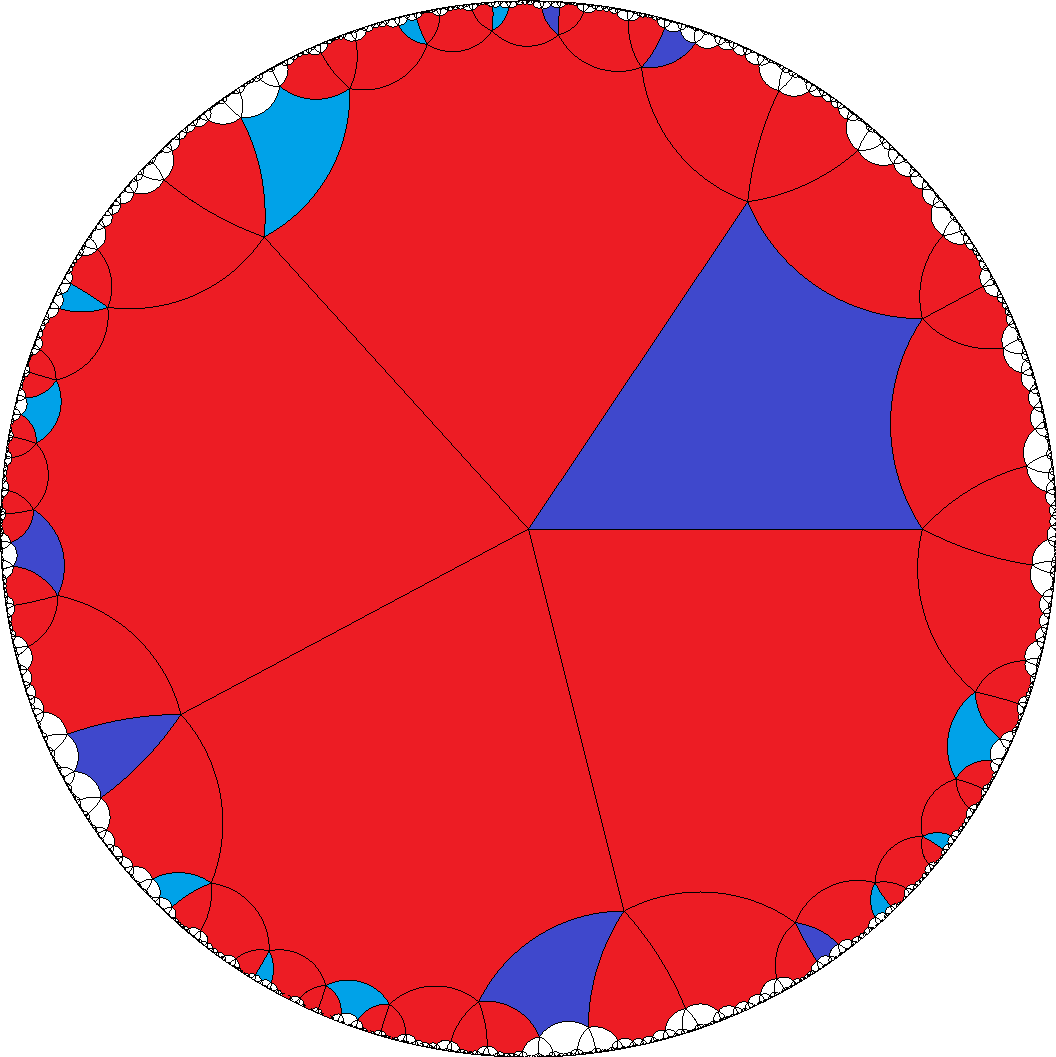 , ...
, ...
-
The single sixth case provides
a1 = AG... and
a2 = DF....
Thus a-gons have to be even here, while tiles b = H... have no restriction.
– This in fact is the most symmetrical version of all here possible cases. It even has non-chiral vertices.
[4,4,4,4,3] 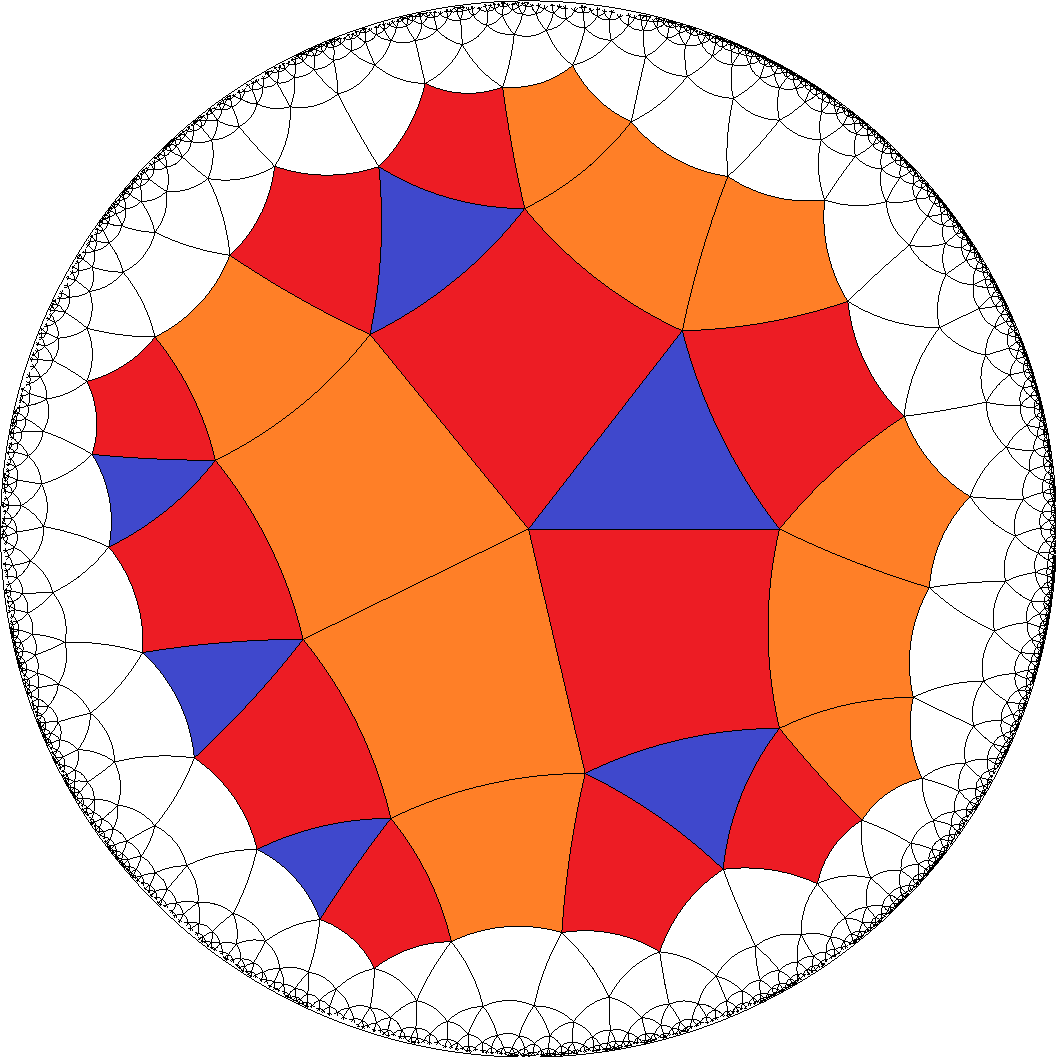 , [6,6,6,6,3]
, [6,6,6,6,3] 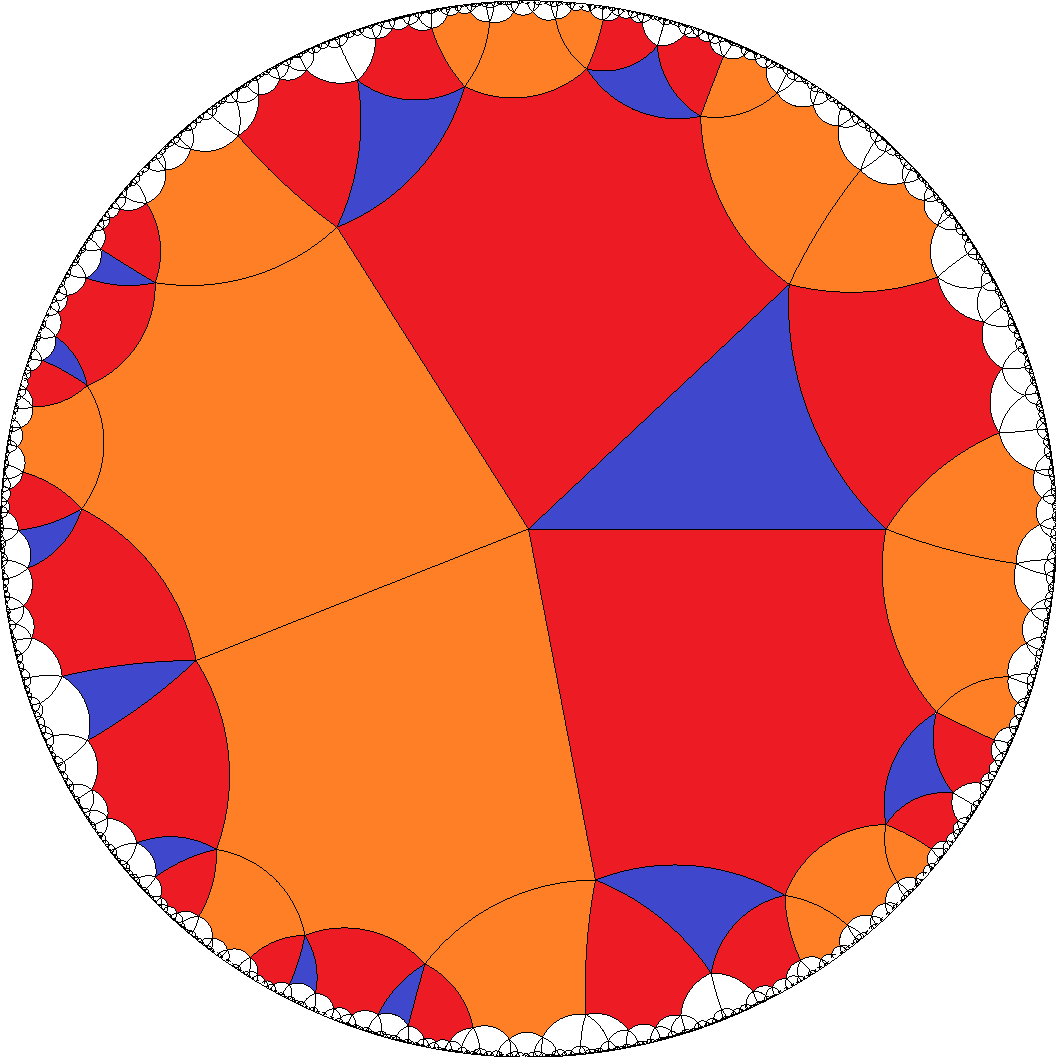 , [6,6,6,6,4]
, [6,6,6,6,4] 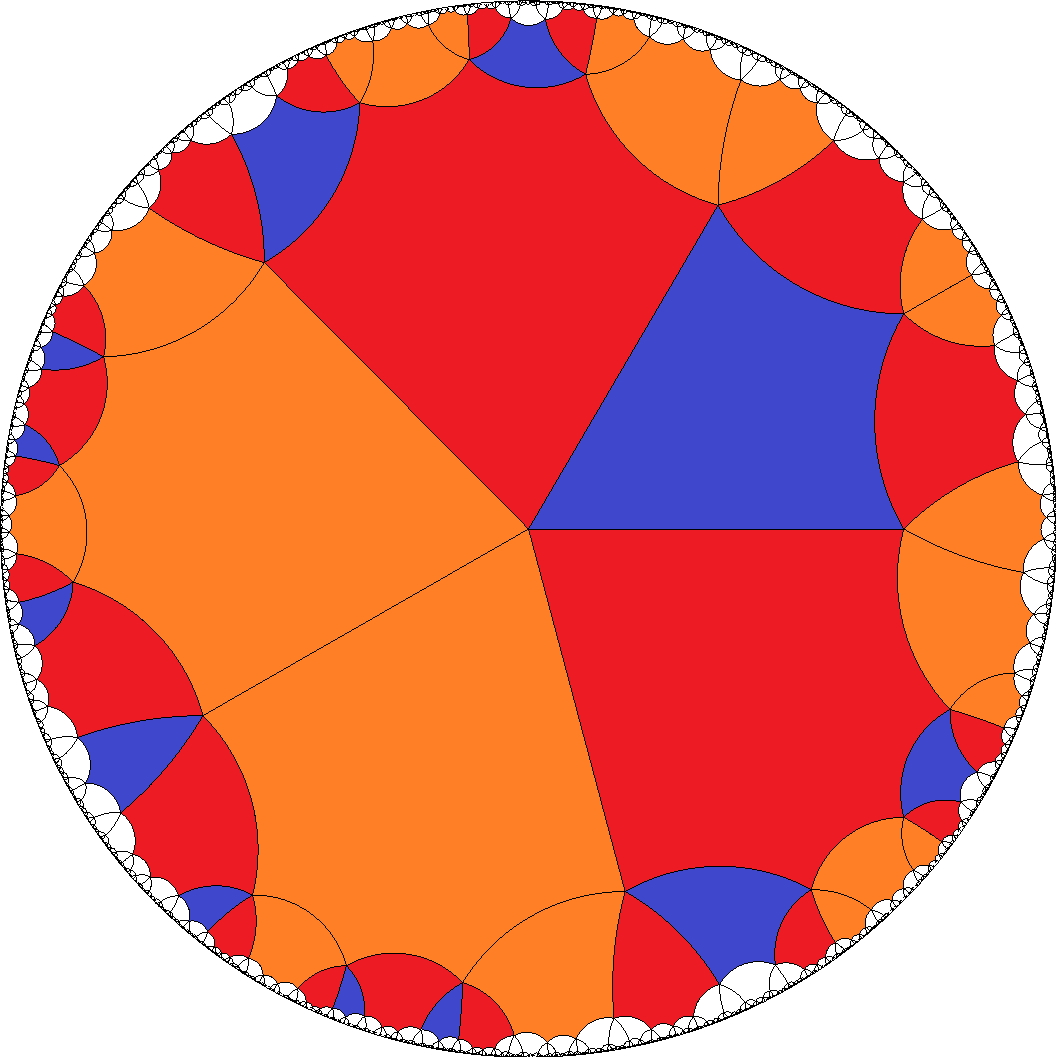 , [8,8,8,8,4]
, [8,8,8,8,4] 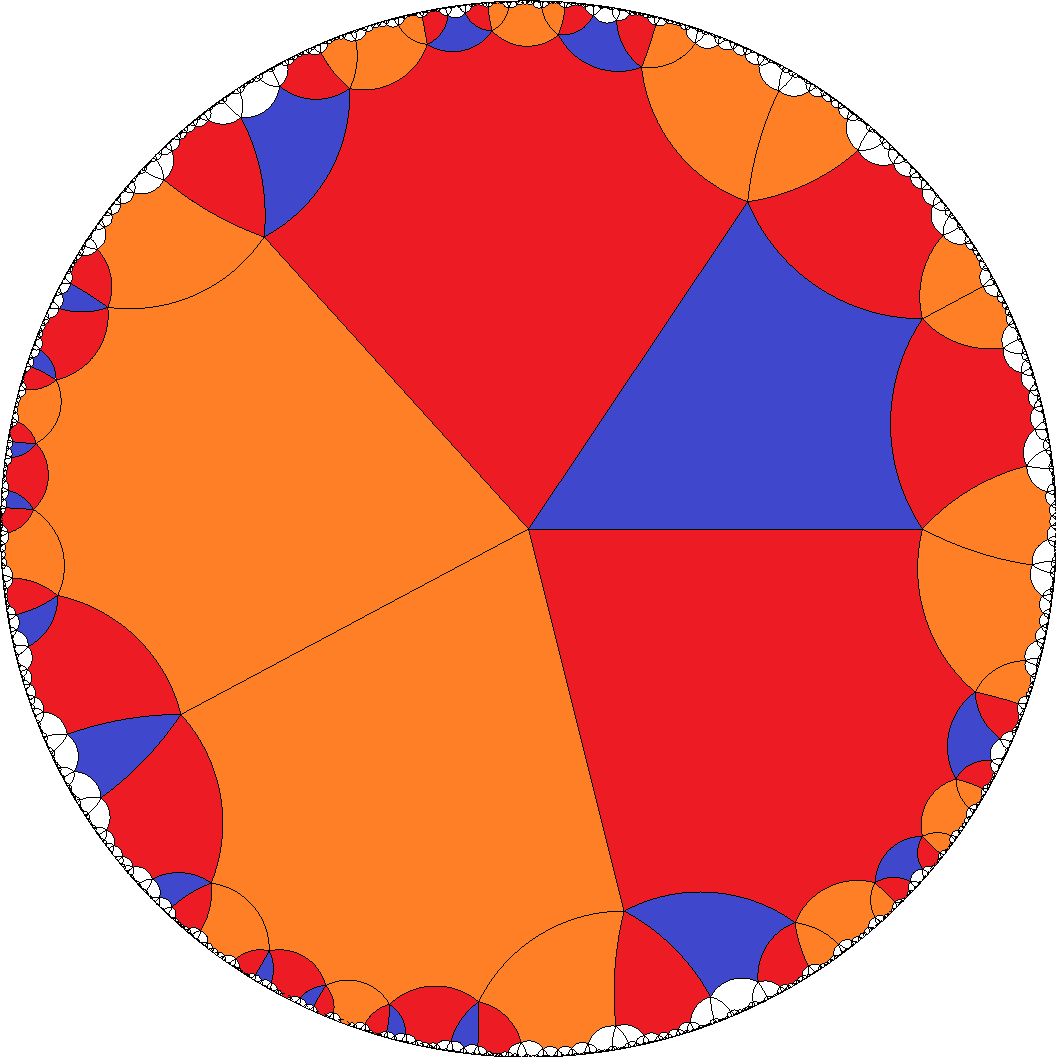 , ...
, ...
-
The eighth group then either allows for the pure sequences
a1 = AG... and
a2 = AE2C1DC2E1..., so
a-gons have to be divisible by 6 once more and tiles b = H... have to be even again.
[6,6,6,6,4] 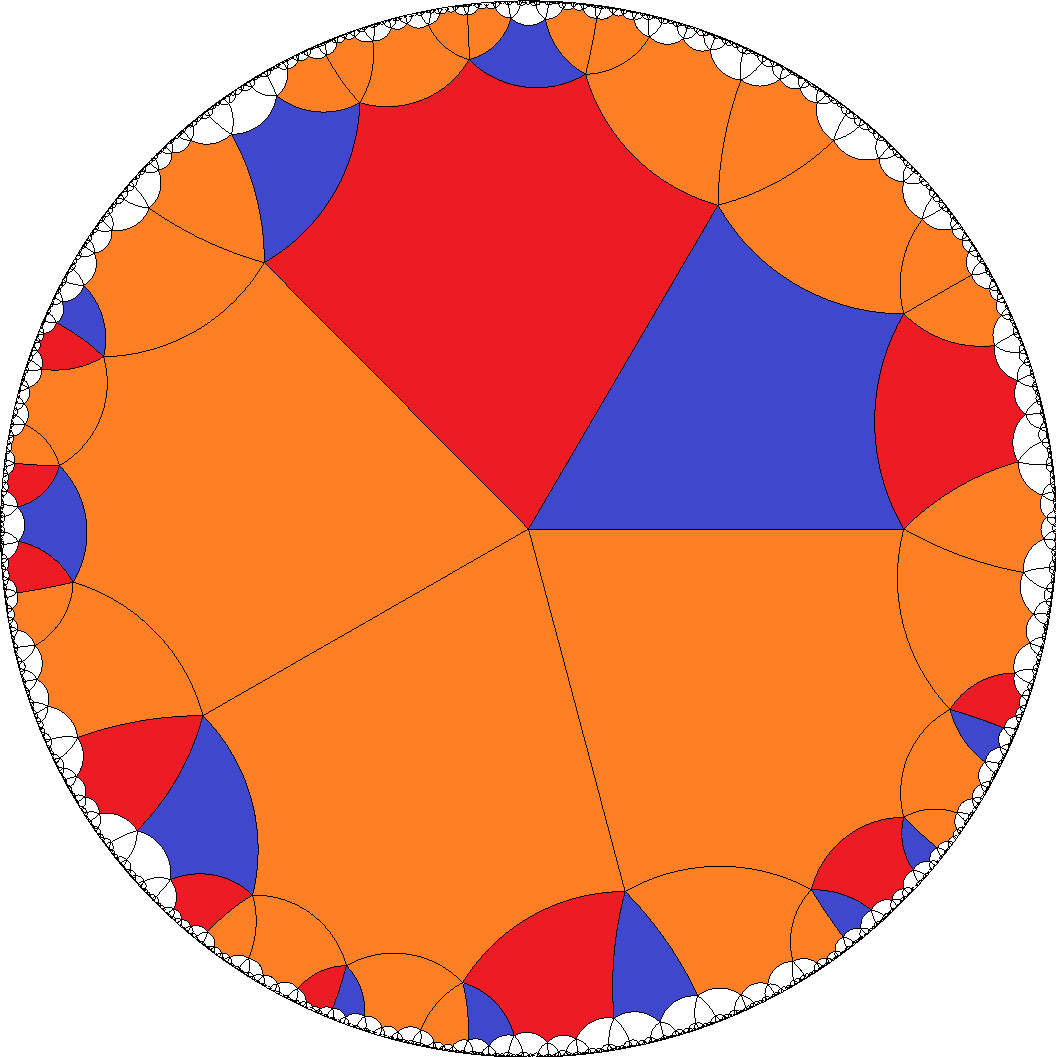 , ...
, ...
-
Alternatively it allows for the mixed sequence
a = AGAE2C1DC2E1..., which then has to be divisible by 8.
For tiles b = H... no restriction is active here.
[8,8,8,8,4] 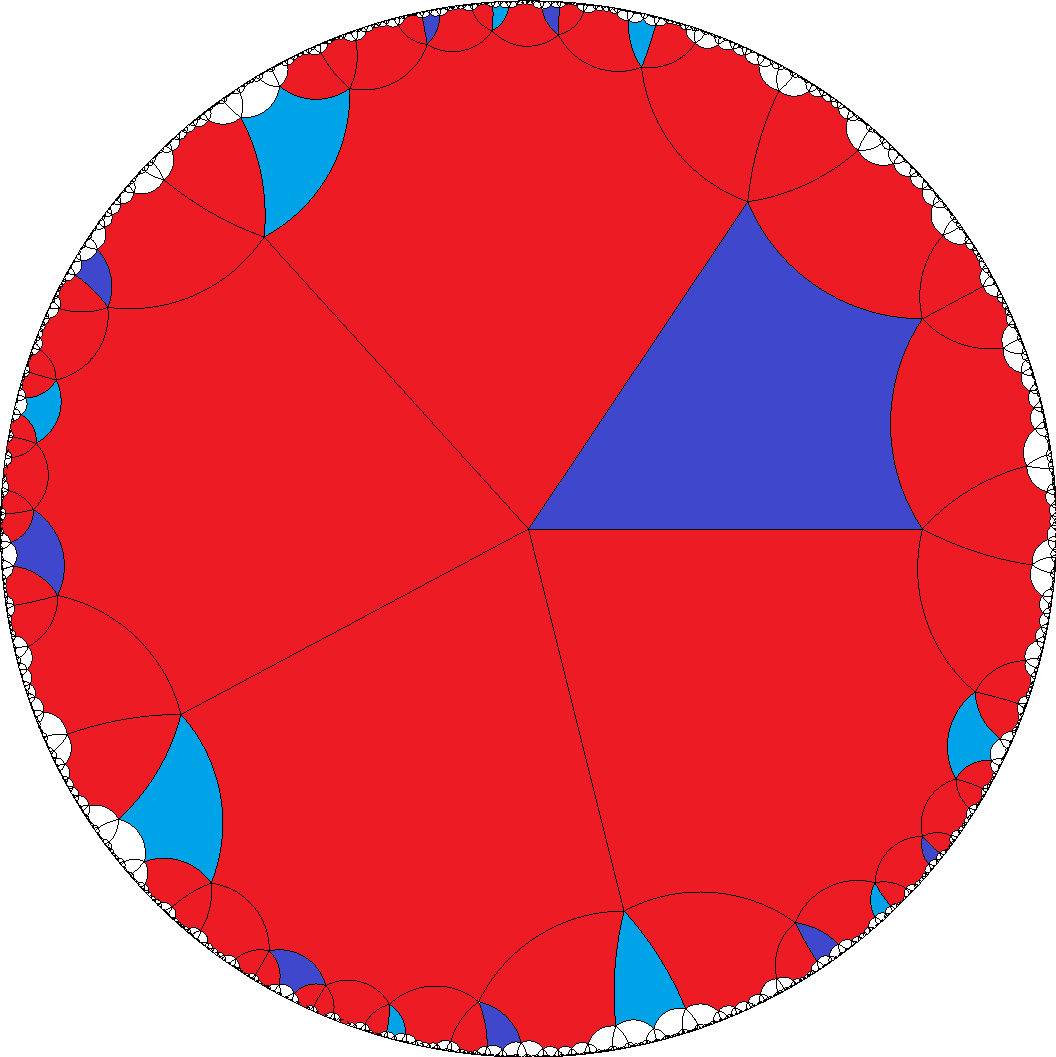 , ...
, ...
-
The ninth group above either allows for the pure sequences
a1 = AE2C1B1... and
a2 = AB2C2E1..., which in fact is an enantiomorph pair.
These tiles then clearly ask for divisibility by 4. For tiles b = H... this looks like having to be even again,
but instead those just fall into an enantiomorph pair instead. That case provides an outer symmetry switching between
vertices with incident b1 and those with b2.
[4,4,4,4,3] 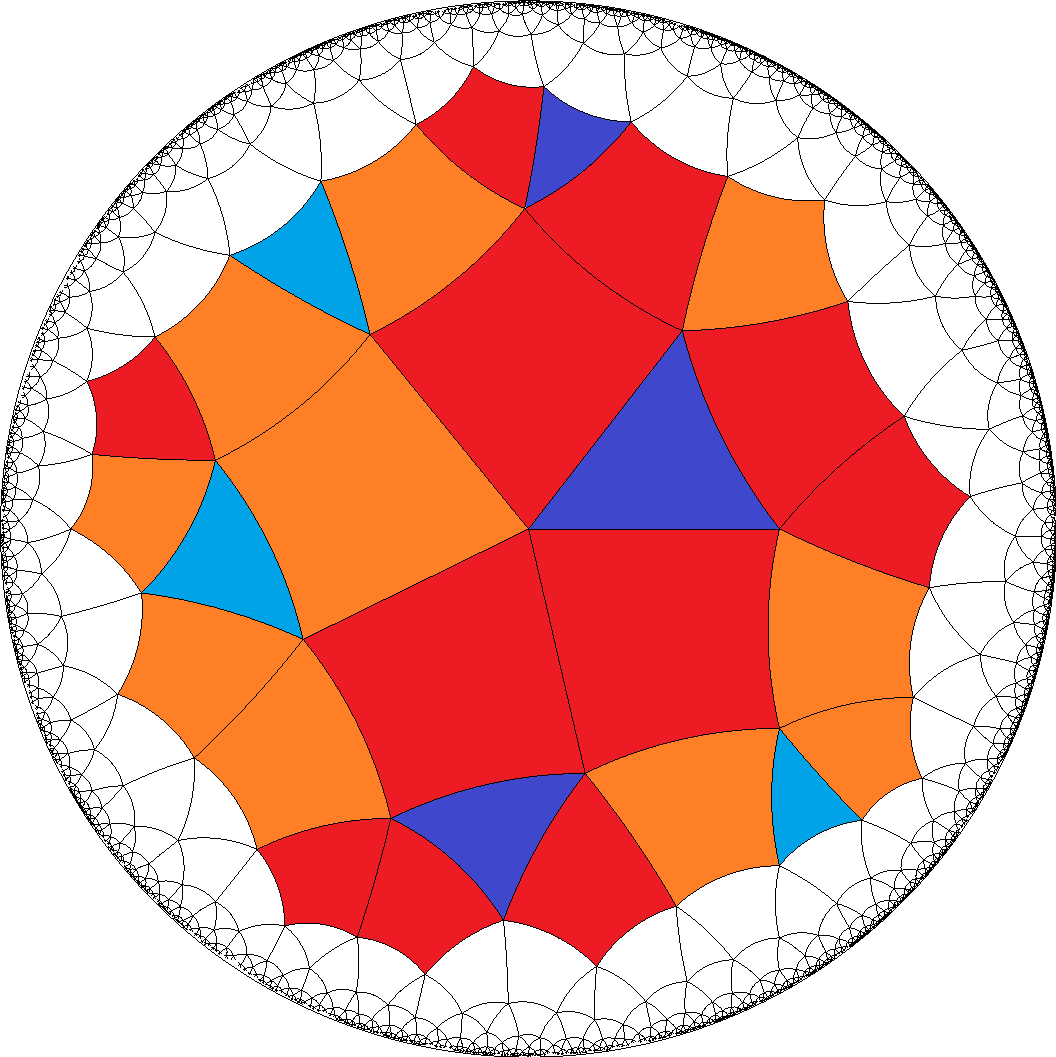 , [4,4,4,4,6]
, [4,4,4,4,6] 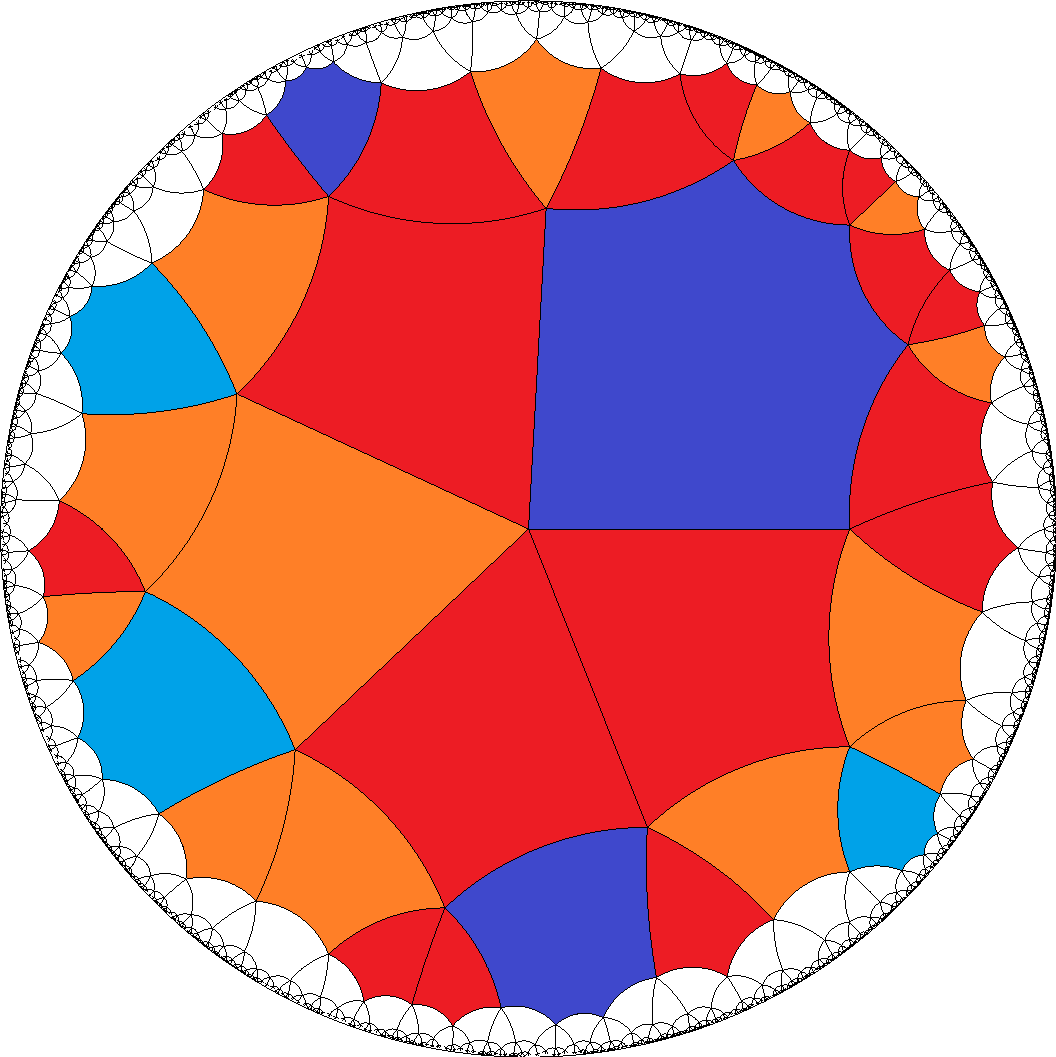 , [8,8,8,8,3]
, [8,8,8,8,3] 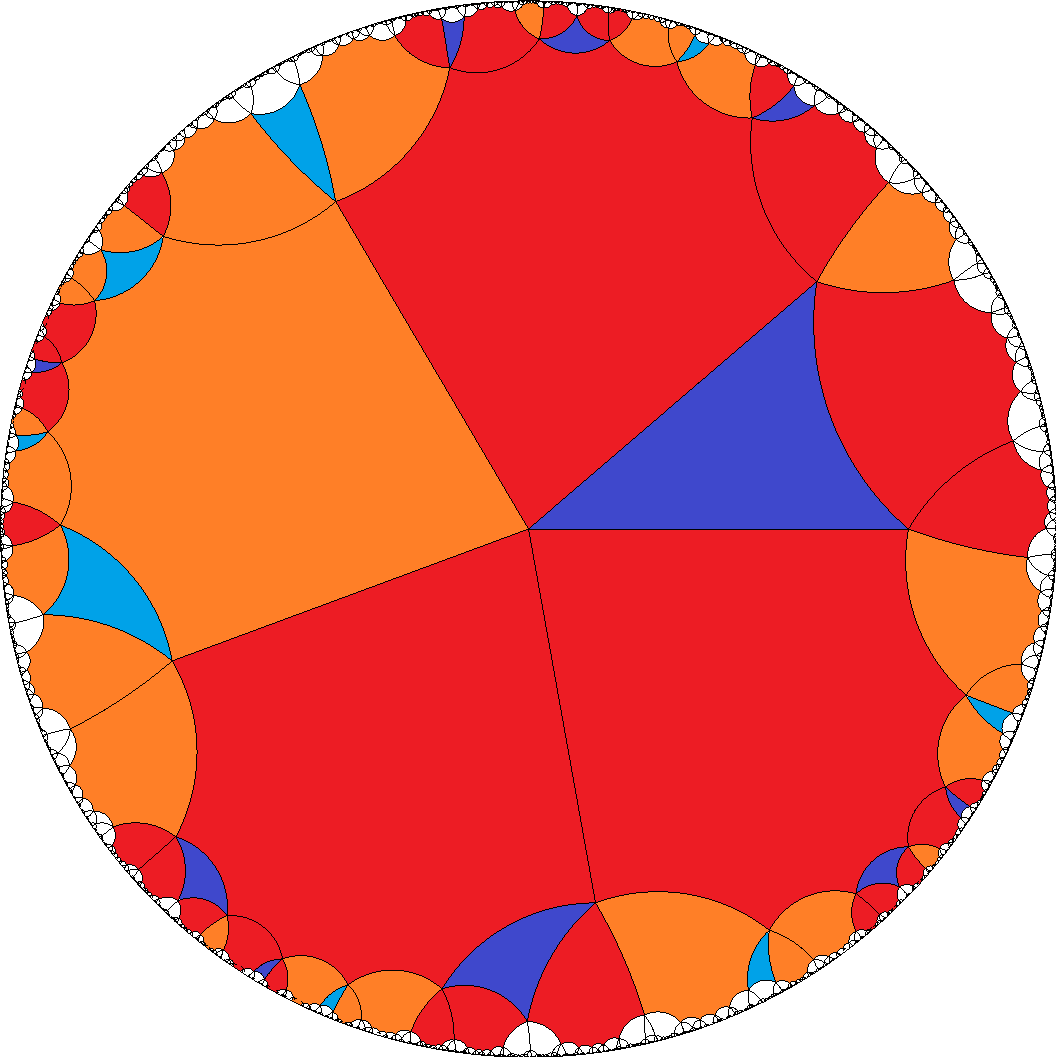 , [8,8,8,8,4]
, [8,8,8,8,4] 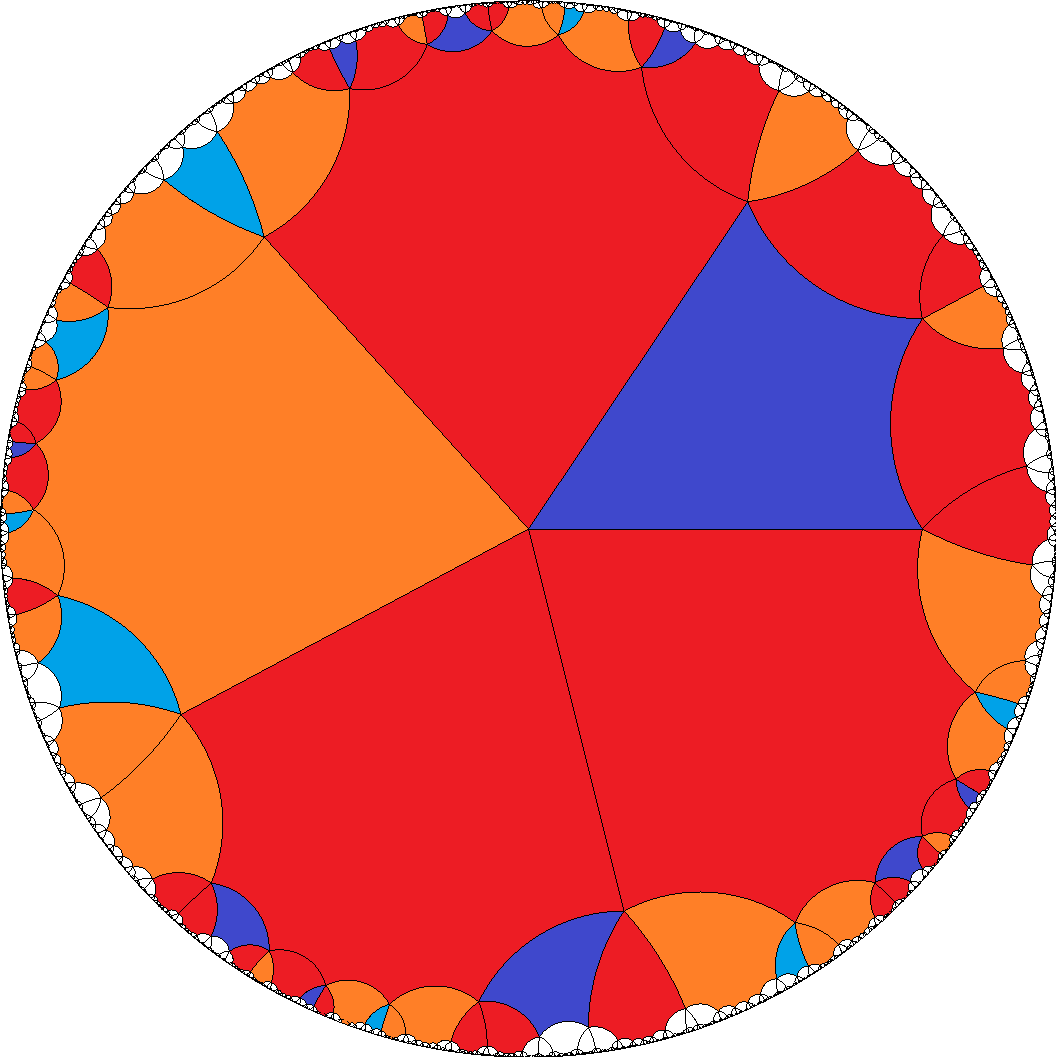 , ...
, ...
-
Alternatively it allows for the mixed sequence
a = AE2C1B1AB2C2E1... with a divisibility by 8.
Tiles b = H... here still have to be even, as their neighbourhoods alternates between the a-regions
...E1AE2... resp. ...B1AB2...
[8,8,8,8,4] 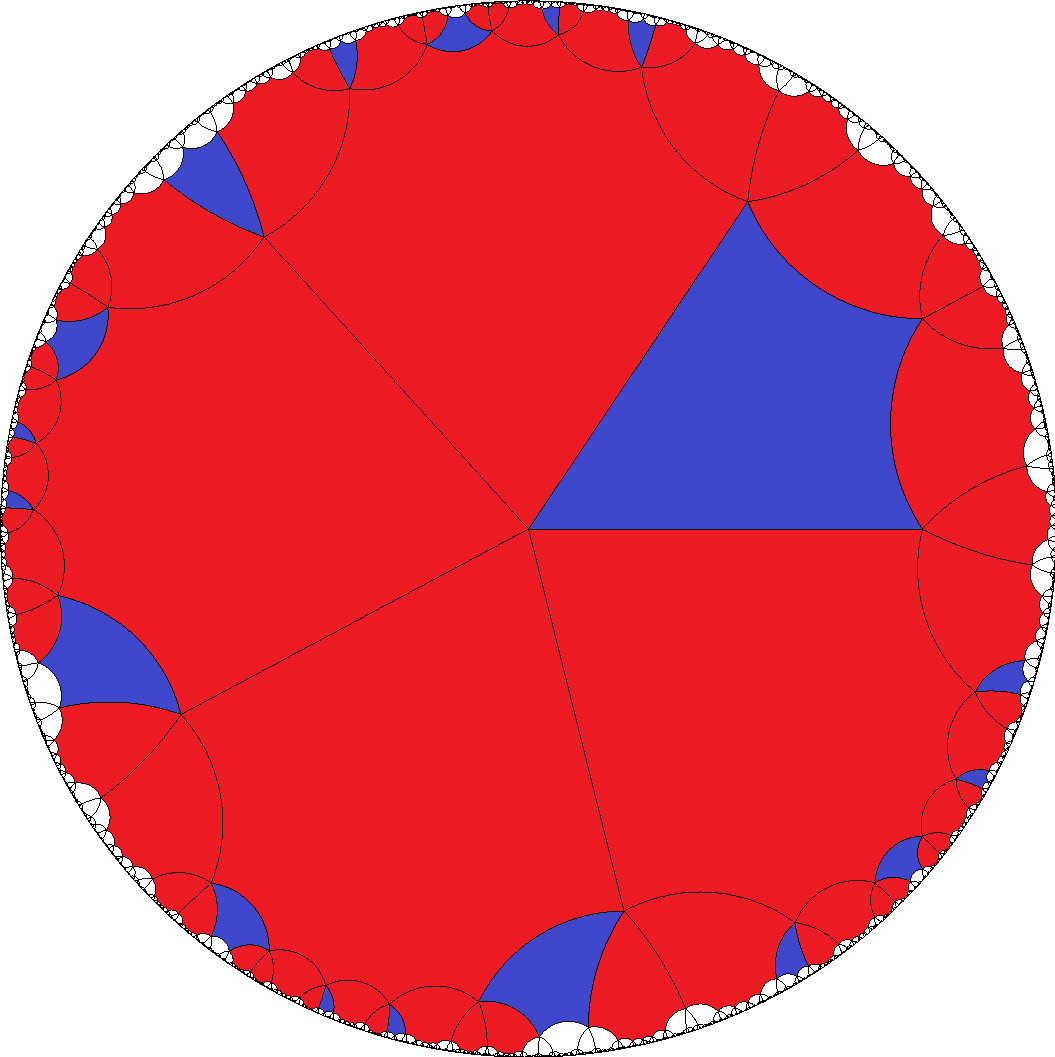 , ...
, ...
-
The thirteenth group then either allows for the enantiomorphe pair of pure sequences
a1 = AE2B1... and
a2 = AB2E1..., together with the further enantiomorphe pair
a3 = C1... and
a4 = C2.... Those thus ask for a divisibility by 3.
And furthermore one might deduce even tiles b = H... – provided both a-pairs each would occur in the same run.
But rather this case breaks up into 2 chiral enantiomorphic subsets:
Either one has the triplet a1, a4, and b; or the other triplet
a2, a3, and b instead. And therefore tiles b thus get no restriction at all.
– This is the case where the snub cube and the snub doedecahedron
(for a = {3} and b = {4} resp. {5}) would be included.
[3,3,3,3,7] 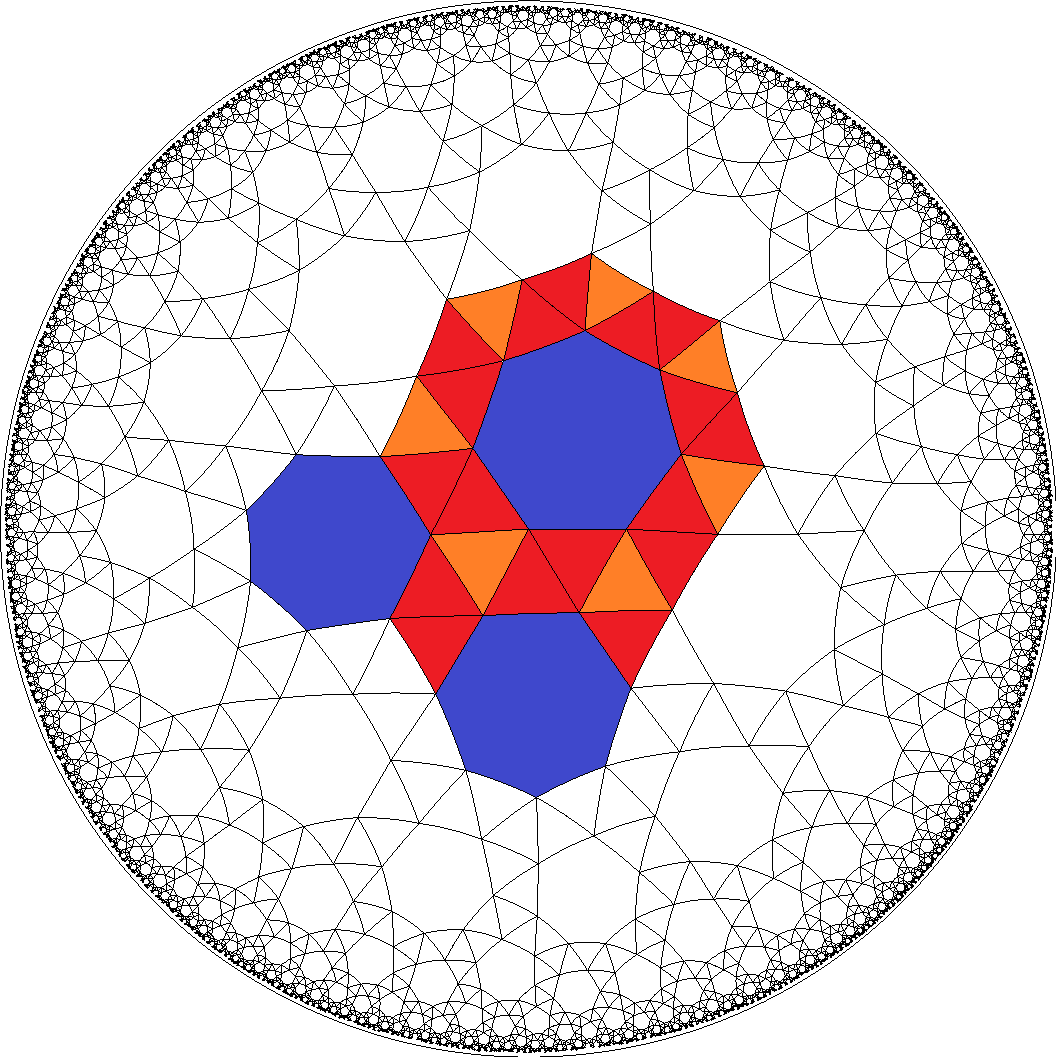 , [6,6,6,6,3]
, [6,6,6,6,3] 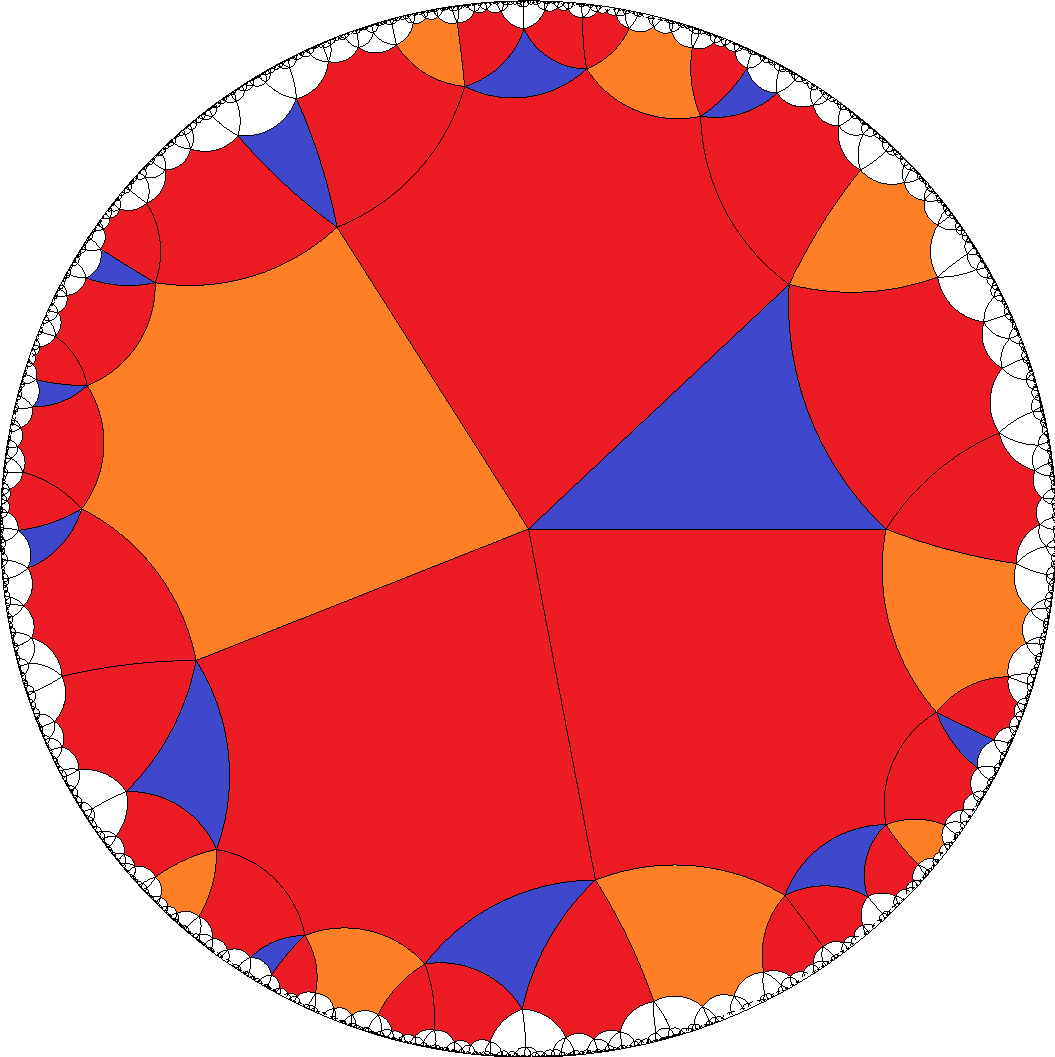 , [6,6,6,6,4]
, [6,6,6,6,4] 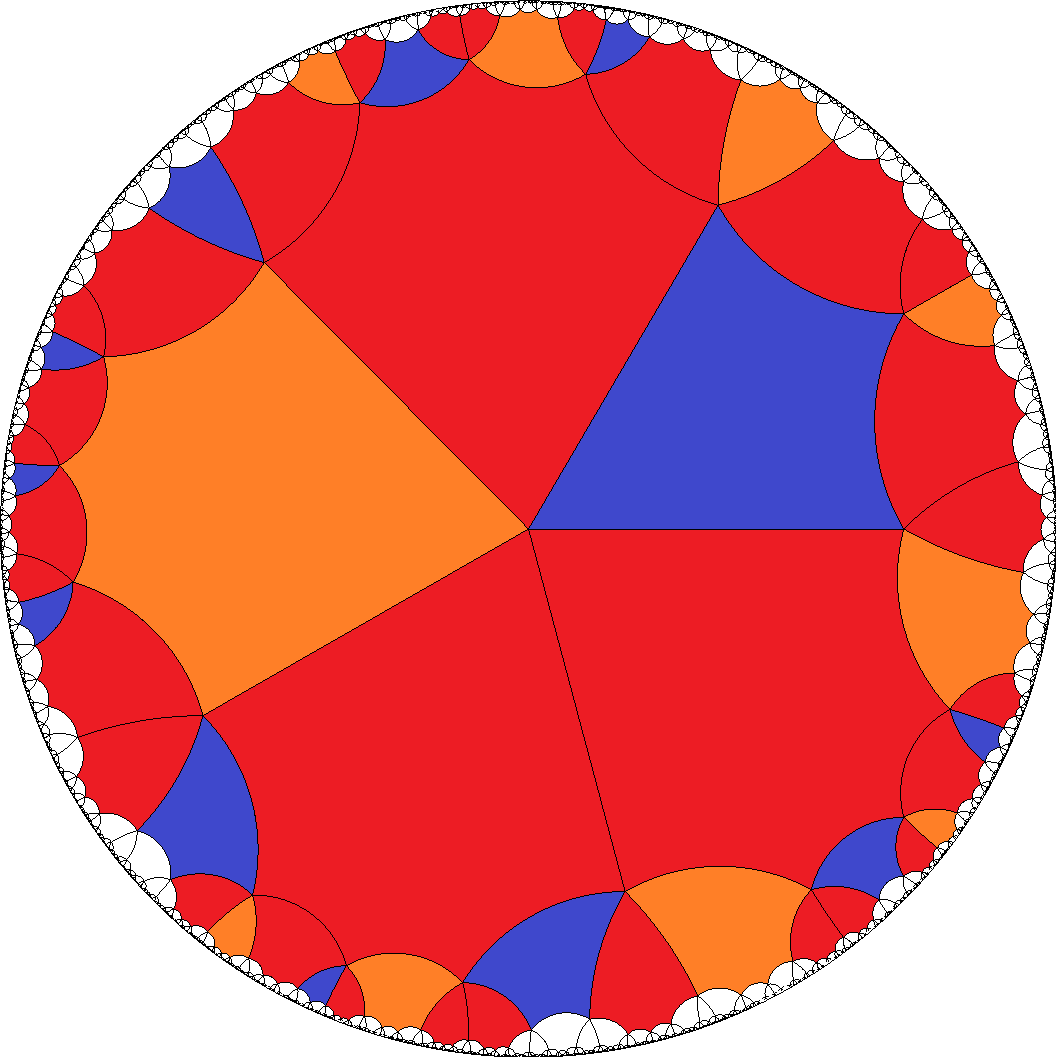 , ...
, ...
-
Alternatively it allows for the mixed sequence
a1 = AE2B1AB2E1...
and again an enantiomorphe pair
a2 = C1... and
a3 = C2.... Those then ask for a divisibility by 6.
And furthermore one has even tiles b = H..., again because their neighbourhoods alternates between the a-regions
...E1AE2... resp. ...B1AB2...
[6,6,6,6,4] 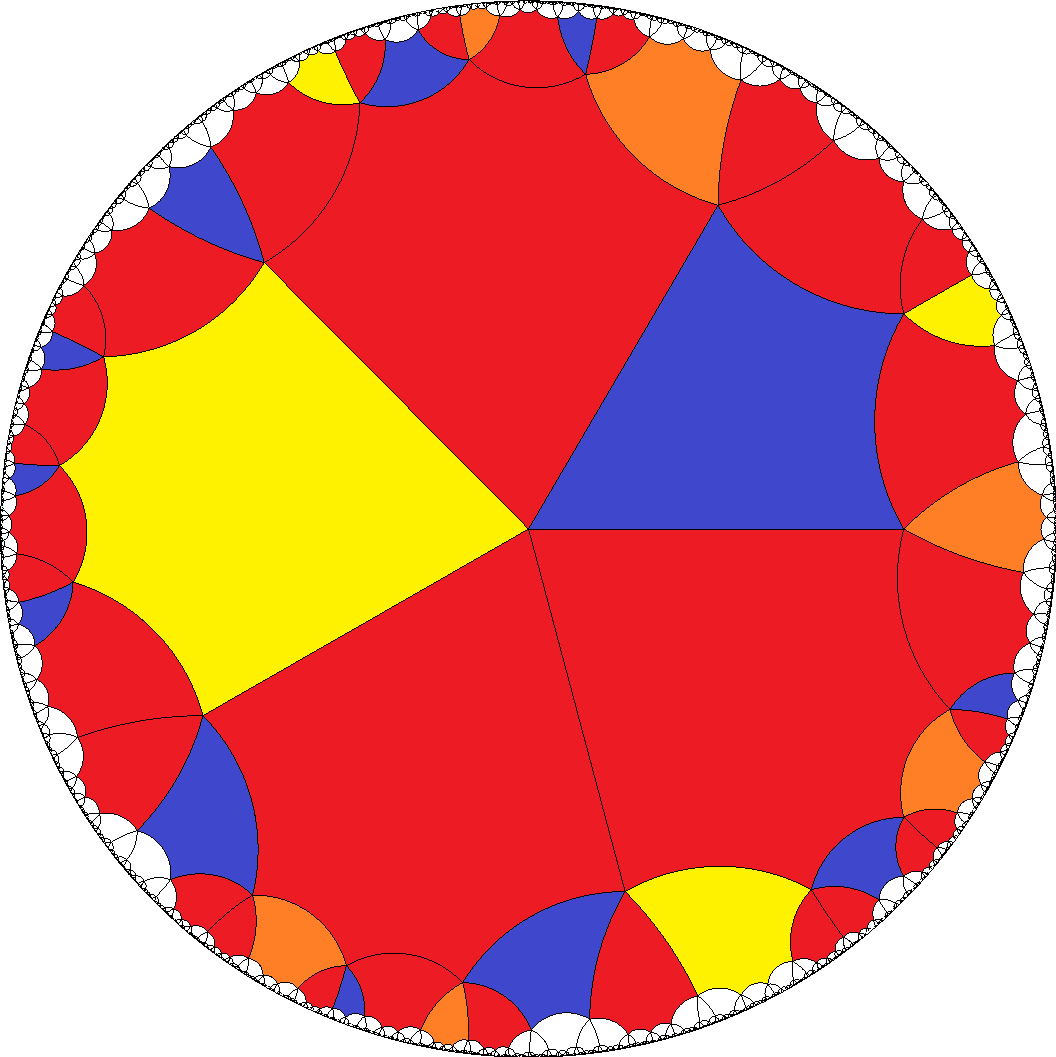 , ...
, ...
-
In the single last case above we just get
a = AB2FB1... and b = H....
Accordingly a-gons have to be divisible by 4, and there is no restriction on tiles b.
[4,4,4,4,3] 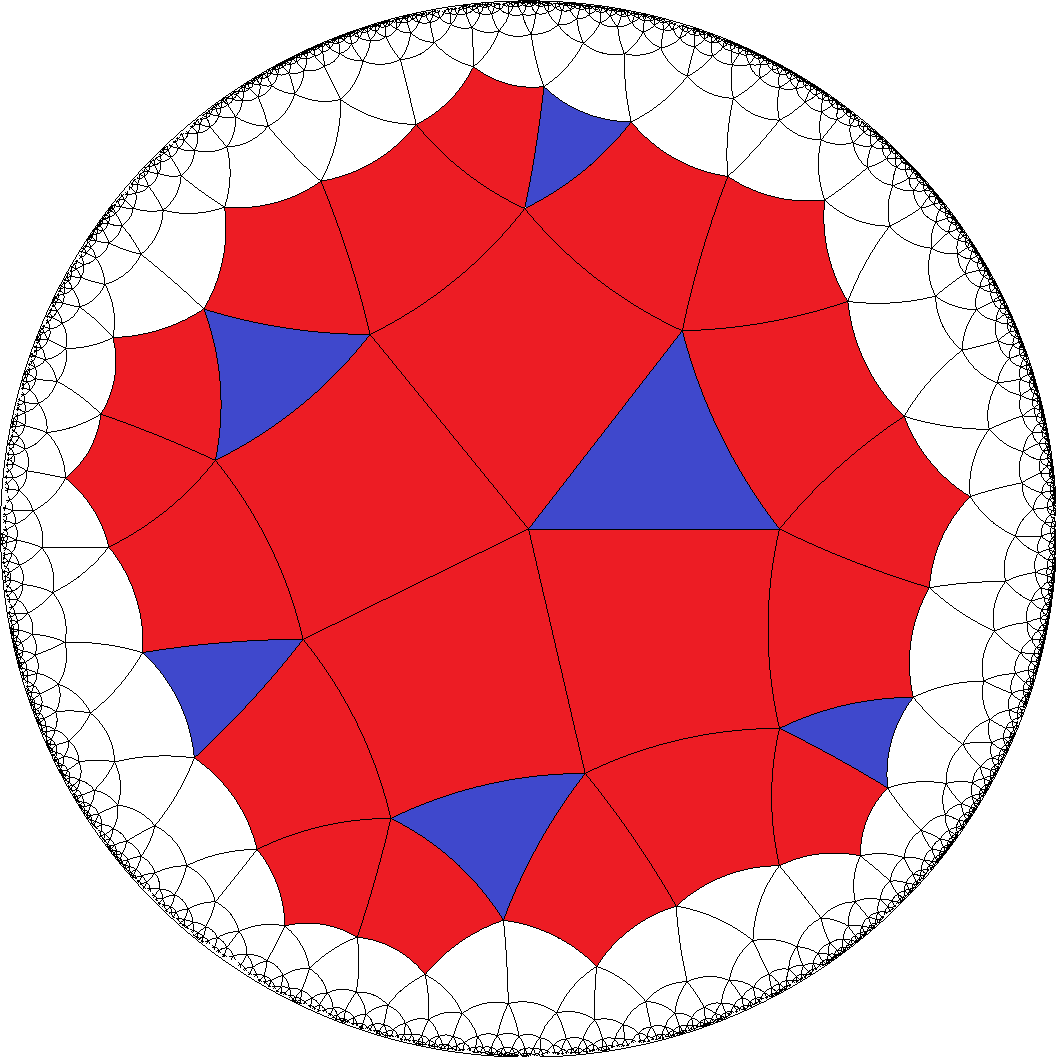 , [4,4,4,4,6]
, [4,4,4,4,6] 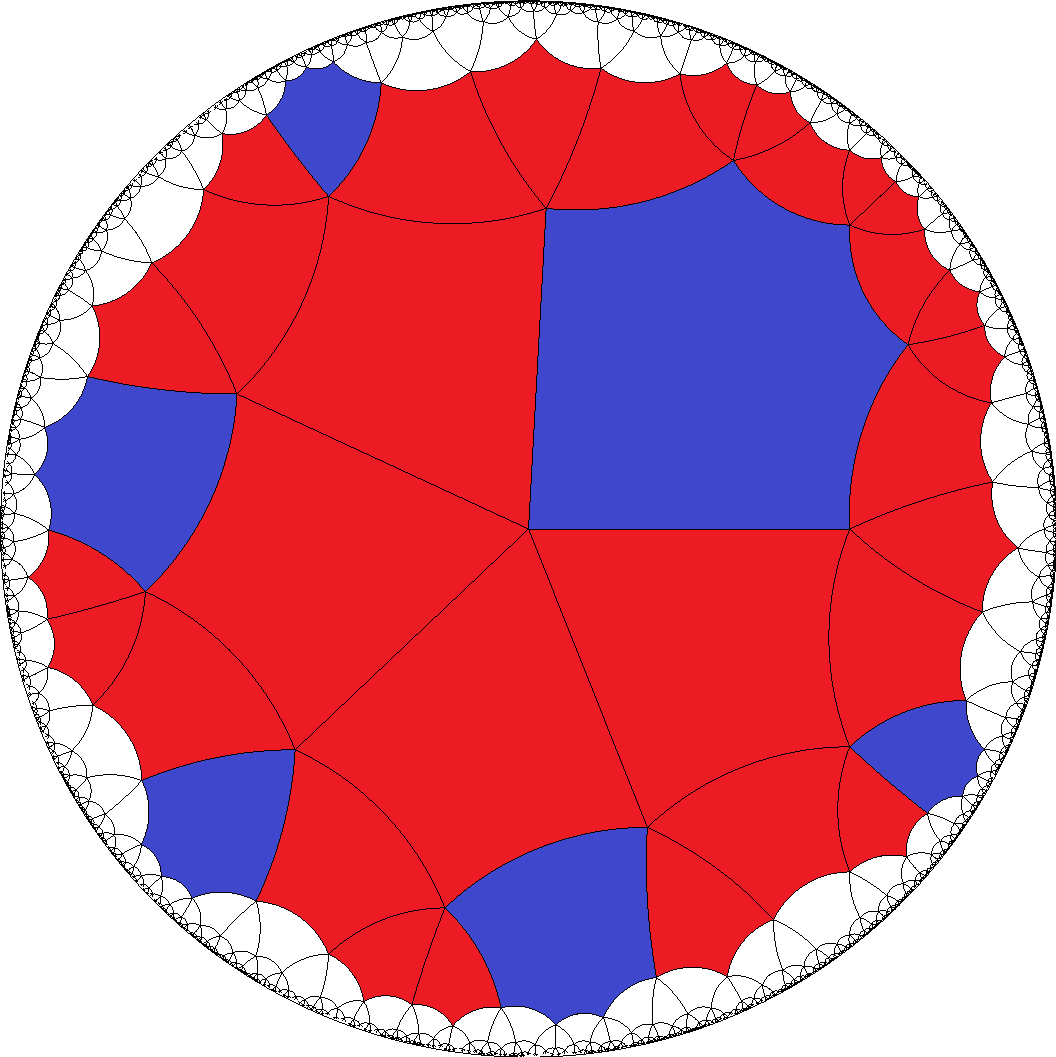 , [8,8,8,8,3]
, [8,8,8,8,3] 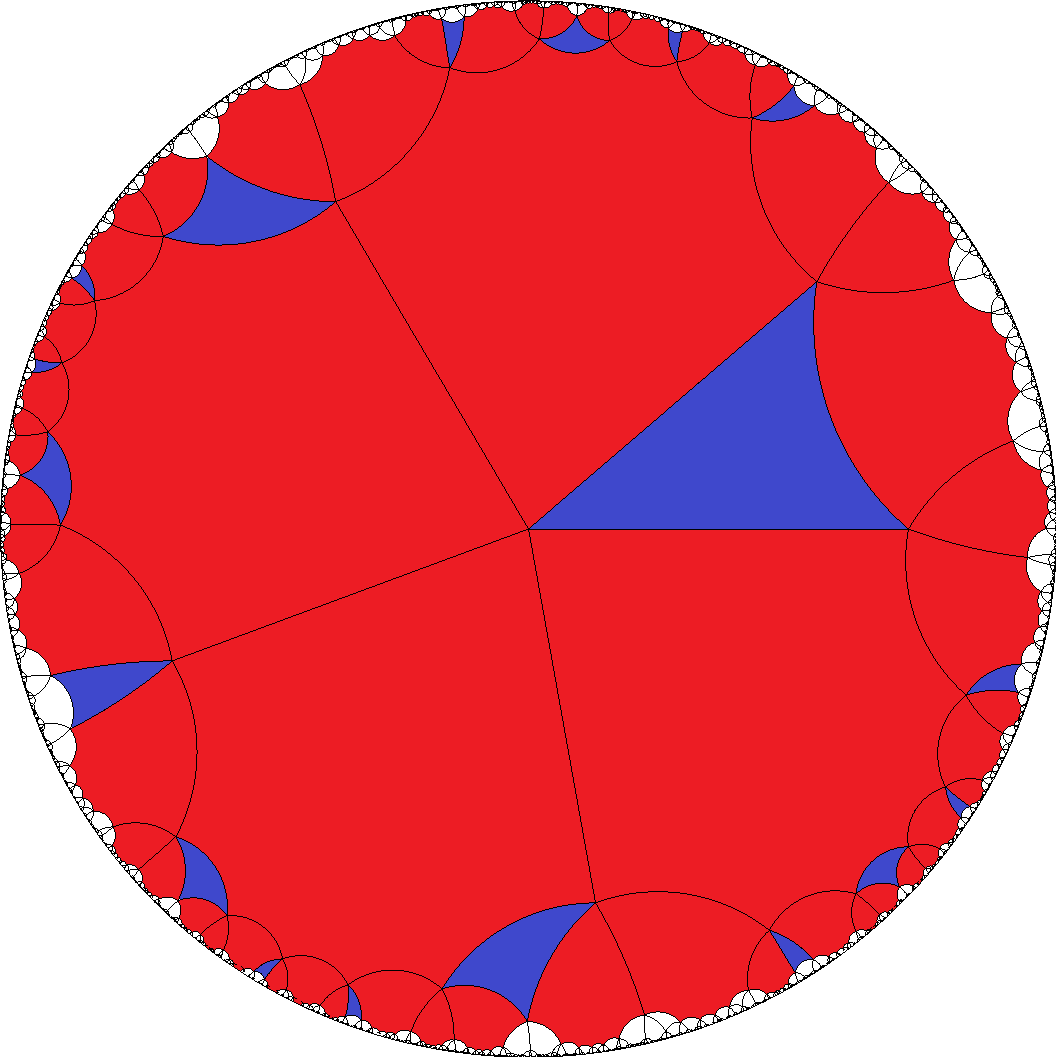 , [8,8,8,8,4]
, [8,8,8,8,4] 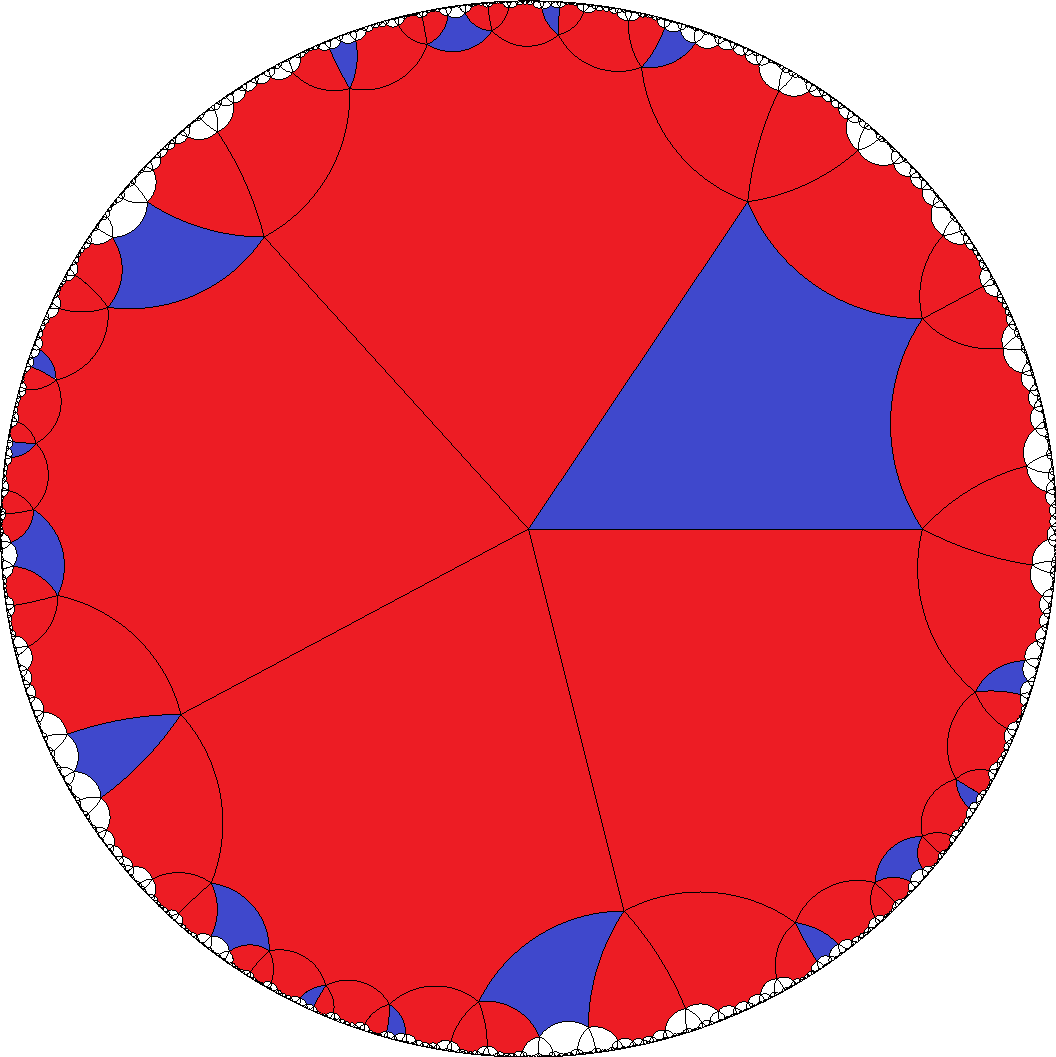 , ...
, ...
The least case, which shows up all of the 14 possibilities, therefore would be [244,4]. Obviously numbers much too high to display
the tiling differences within according Poincaré disc displays each. Instead we provide in addition to the above grouping of several examples of
tilings per case also a regrouping of different tiling cases per divisibility.
|
3|a
|
1|b
|
a=3, b=7
|
12 
|
|
4|a
|
1|b
|
a=4, b=3
|
7  ,
10 ,
10  ,
14 ,
14 
|
|
4|a
|
2|b
|
a=4, b=6
|
1  ,
3 ,
3  ,
7 ,
7 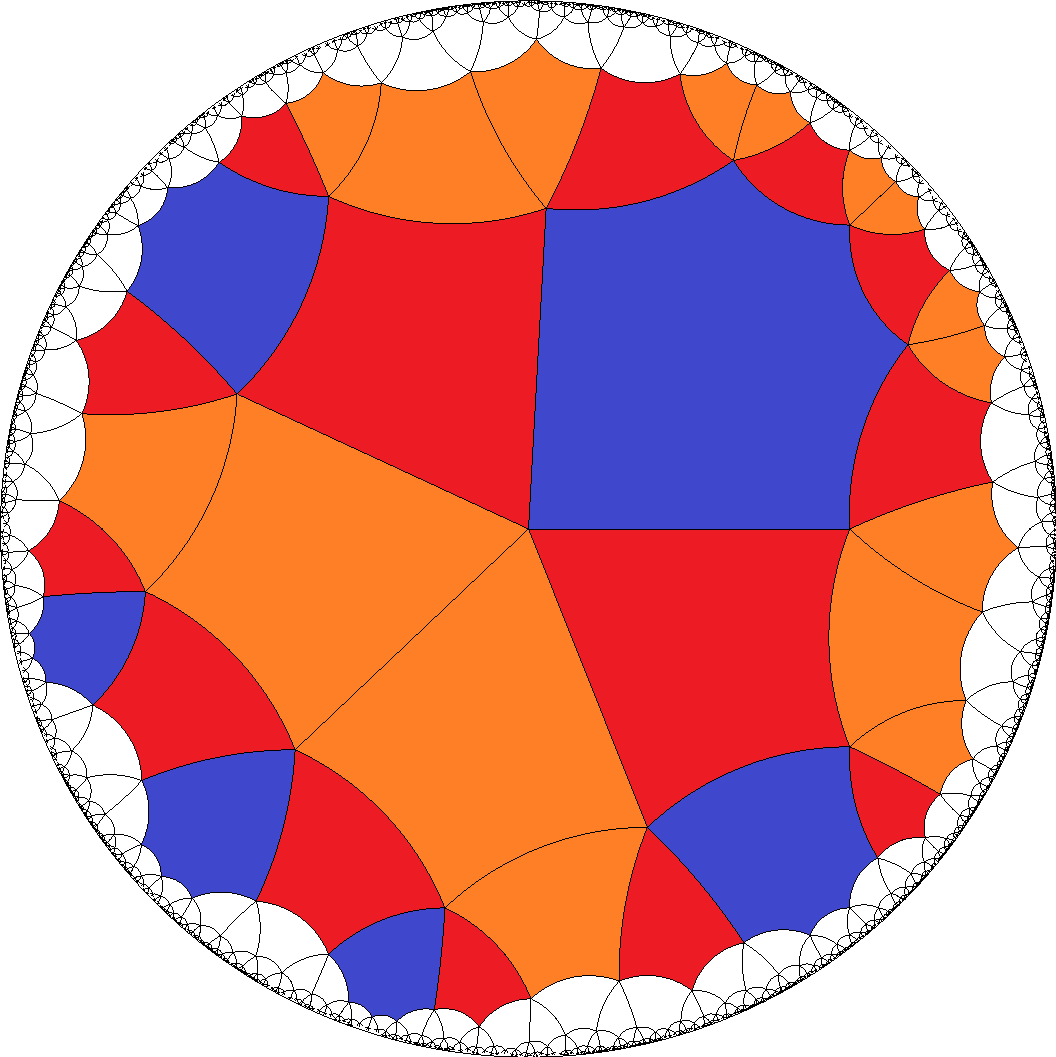 ,
10 ,
10  ,
14 ,
14 
|
|
6|a
|
1|b
|
a=6, b=3
|
2  ,
4 ,
4  ,
7 ,
7  ,
12 ,
12 
|
|
6|a
|
2|b
|
a=6, b=4
|
2  ,
4 ,
4  ,
5 ,
5  ,
7 ,
7  ,
8 ,
8  ,
12 ,
12  ,
13 ,
13 
|
|
8|a
|
1|b
|
a=8, b=3
|
6 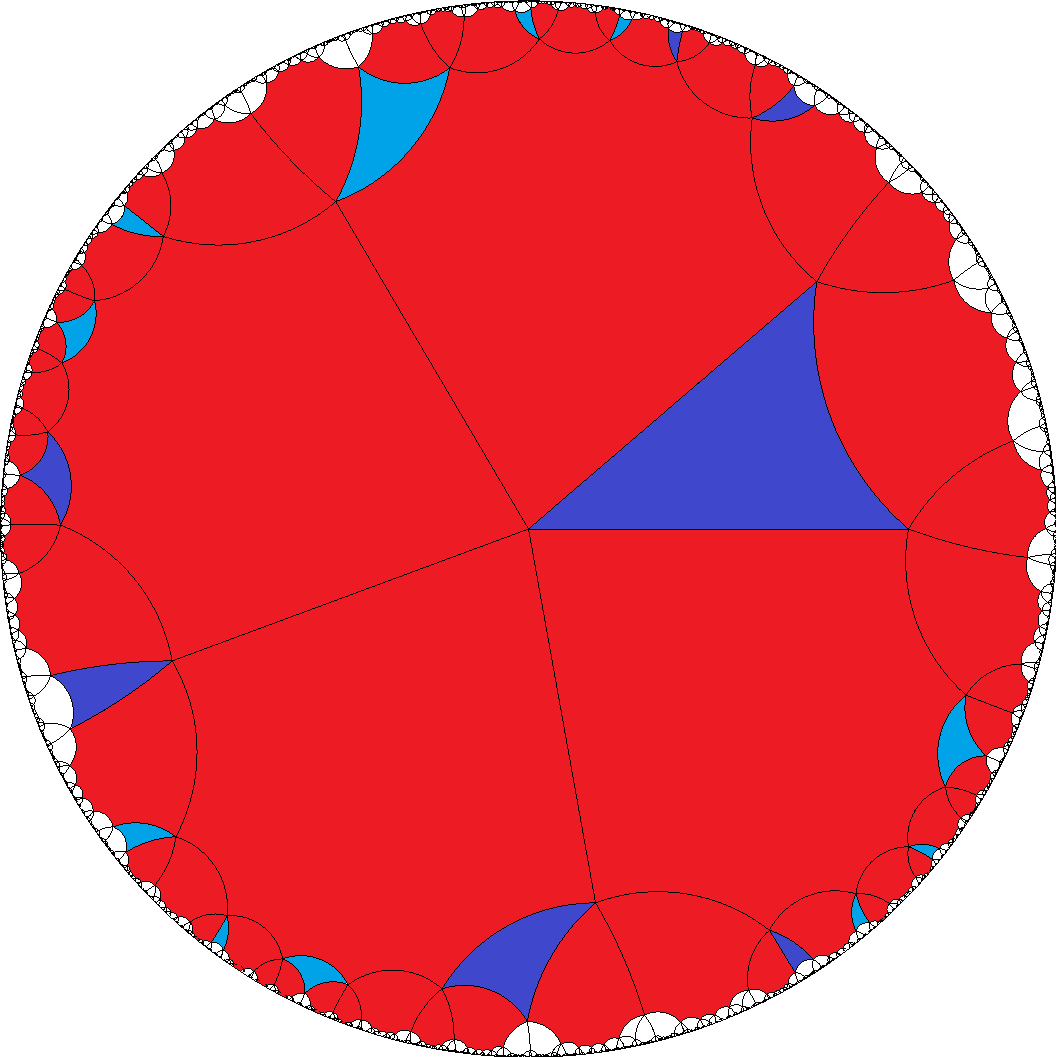 ,
7 ,
7 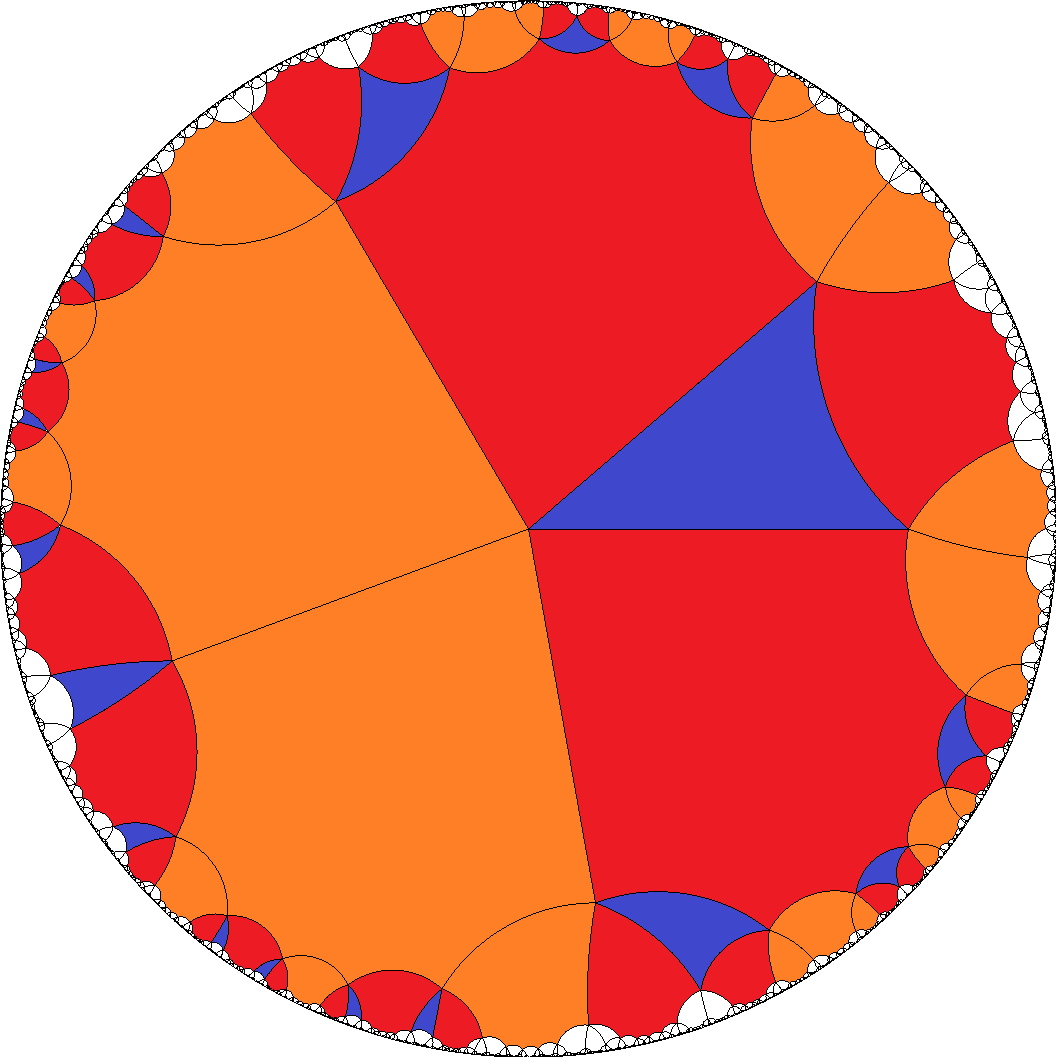 ,
9 ,
9 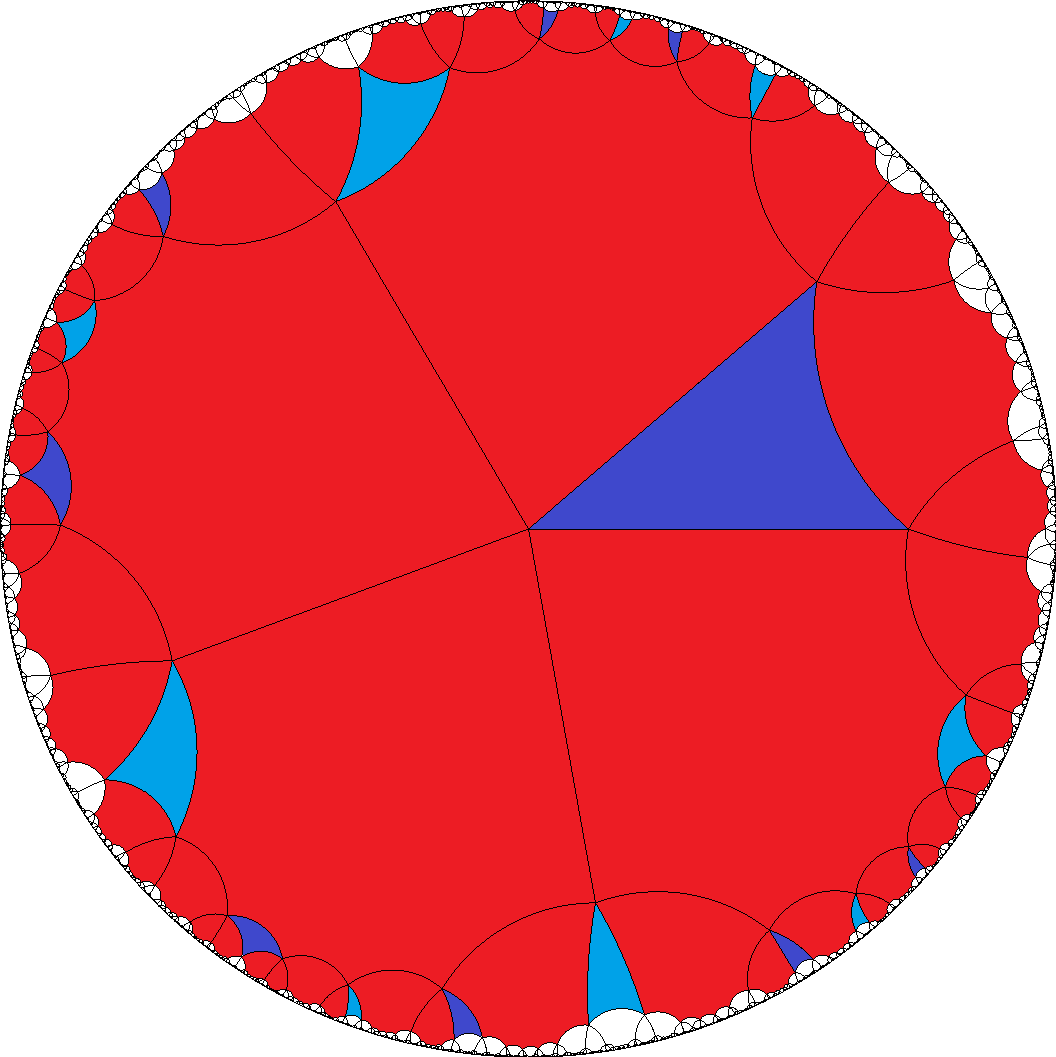 ,
14 ,
14 
|
|
8|a
|
2|b
|
a=8, b=4
|
1  ,
3 ,
3  ,
6 ,
6  ,
7 ,
7  ,
9 ,
9  ,
10 ,
10  ,
11 ,
11  ,
14 ,
14 
|
© – All the pics on [a,a,a,a,b] generously have been privately provided by M. Čtrnáct.
Used colorings only aid for distinction; none the less all cases are uniform.
Esp. yellow and green tiles resp. light and dark blue ones (and in case 10 also red and orange ones) often just distinguish enantiomorph pairings,
although they would be symmetry equivalent.




 , [8,8,8,8,4]
, [8,8,8,8,4]  , ...
, ...
 , [6,6,6,6,4]
, [6,6,6,6,4]  , ...
, ...
 , [8,8,8,8,4]
, [8,8,8,8,4]  , ...
, ...
 , [6,6,6,6,4]
, [6,6,6,6,4]  , ...
, ...
 , ...
, ...
 , ...
, ...
 , [6,6,6,6,3]
, [6,6,6,6,3]  , [6,6,6,6,4]
, [6,6,6,6,4]  , [8,8,8,8,4]
, [8,8,8,8,4]  , ...
, ...
 , ...
, ...
 , ...
, ...
 , [4,4,4,4,6]
, [4,4,4,4,6]  , [8,8,8,8,3]
, [8,8,8,8,3]  , [8,8,8,8,4]
, [8,8,8,8,4]  , ...
, ...
 , ...
, ...
 , [6,6,6,6,3]
, [6,6,6,6,3]  , [6,6,6,6,4]
, [6,6,6,6,4]  , ...
, ...
 , ...
, ...
 , [4,4,4,4,6]
, [4,4,4,4,6]  , [8,8,8,8,3]
, [8,8,8,8,3]  , [8,8,8,8,4]
, [8,8,8,8,4]  , ...
, ...
 ,
10
,
10  ,
7
,
7  ,
9
,
9  ,
14
,
14