Acronym	sishi, spD
Name	small stellated hecatonicosachoron, stellated polydodecahedron
Cross sections	©
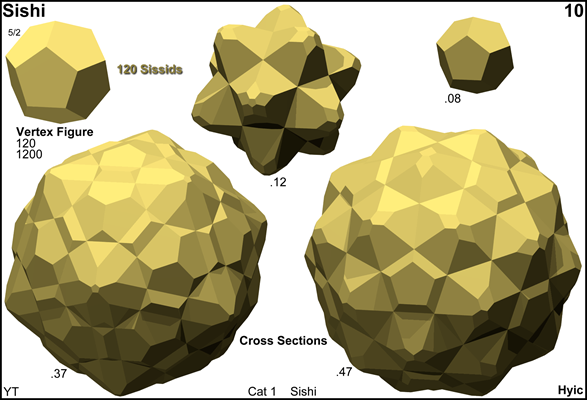Circumradius	1
Inradius	(1+sqrt(5))/4 = 0.809017
Density	4
Vertex figure	doe
Lace city in approx. ASCII-art	©   o5o o5o o5v v5o v5o o5o o5o x5o o5x o5x o5v o5v x5o x5o o5o v5v o5o o5x o5x v5o v5o x5o x5o o5x o5o o5o o5v o5v v5o o5o o5o
	©   o3o v3o o3x x3o o3v o3o o3x x3v v3x x3o o3o x3o o3f f3o o3x o3v v3x f3o x3x o3f x3v v3o x3o o3f f3o o3x o3o o3x x3v v3x x3o o3o v3o o3x x3o o3v o3o
	©   o2o o2v x2o x2f x2o o2v v2o x2x o2f f2v o2f x2x v2o o2x f2o x2f f2o o2x o2o f2x v2f f2x uo2ou f2x v2f f2x o2o o2x f2o x2f f2o o2x v2o x2x o2f f2v o2f x2x v2o o2v x2o x2f x2o o2v o2o
Coordinates	(1, 0, 0, 0)                                         & all permutations, all changes of sign (vertex inscribed q-hex) (1/2, 1/2, 1/2, 1/2)                             & all permutations, all changes of sign (vertex inscribed tes) ((1+sqrt(5))/4, (sqrt(5)-1)/4, 1/4, 0)   & all even permutations, all changes of sign (vertex inscribed v-sadi)
General of army	ex
Colonel of regiment	(is itself locally convex – uniform polychoral members: by cells: co ditdid gad gidtid gike ike oct oho pip sidtid sissid stip tet thah trip sadixhix (compound) 300 0 0 0 0 0 0 0 0 0 0 0 0 600 0 gadixhix (compound) 300 0 0 0 0 0 0 0 0 0 0 0 0 600 0 idhi 0 120 0 0 0 0 0 0 0 0 0 0 0 0 0 gaghi 0 0 120 0 0 0 0 0 0 0 0 0 0 0 0 didhi 0 0 0 120 120 0 0 0 0 0 0 0 0 0 0 gitpodady (fissary) 0 0 0 120 0 120 0 0 0 0 0 0 0 0 0 sridixhi 0 0 0 120 0 0 0 0 0 0 0 0 600 0 0 dittady 0 0 0 0 120 120 0 0 0 0 0 0 0 0 0 sifdahihox (fissary) 0 0 0 0 120 0 0 300 0 0 0 0 0 0 0 sitpodady (fissary) 0 0 0 0 120 0 0 0 0 120 0 0 0 0 0 sidtixhi 0 0 0 0 120 0 0 0 0 0 0 0 600 0 0 sridaphi 0 0 0 0 120 0 0 0 0 0 0 0 0 0 1200 gifdahihox (fissary) 0 0 0 0 0 120 0 300 0 0 0 0 0 0 0 ofiddady 0 0 0 0 0 120 0 0 0 120 0 0 0 0 0 gidtixhi 0 0 0 0 0 120 0 0 0 0 0 0 600 0 0 gridaphi 0 0 0 0 0 120 0 0 0 0 0 0 0 0 1200 dox (compound) 0 0 0 0 0 0 600 0 0 0 0 0 0 0 0 paphacki 0 0 0 0 0 0 0 0 720 0 0 0 0 0 0 gridixhi 0 0 0 0 0 0 0 0 0 120 0 0 600 0 0 sishi 0 0 0 0 0 0 0 0 0 0 120 0 0 0 0 paphicki 0 0 0 0 0 0 0 0 0 0 0 720 0 0 0 getut 0 0 0 0 0 0 0 0 0 0 0 0 480 480 480 setut 0 0 0 0 0 0 0 0 0 0 0 0 480 480 480 & others)
Dual	fix
Dihedral angles	at {5/2} between sissid and sissid:   144°
Face vector	120, 1200, 720, 120
Confer	Grünbaumian relatives: sishi+gaghi+120did   sishi+gaghi+idhi   sishi+gridixhi   sishi+idhi   sishi+ofiddady   sishi+paphicki+gridaphi   2sishi   2sishi+2paphicki   3sishi   6sishi   uniform relatives: gudap   rappisdi   related segmentochora: gikaike   decompositions: pt || sishi   general polytopal classes: Wythoffian polychora   regular   noble polytopes
External links

As abstract polytope sishi is isomorphic to gaghi, thereby replacing pentagrams by pentagons, resp. sissid by gad, resp. replacing doe vertex figures by gissid ones.

Here the sissids form 12 swirling rings of 10 each.

Note that the edge skeleton supports not only sissid or gike cells, but also gad or ike cells. Therefore any single such ring of 10 sissids could well be replaced by a ring of starps (5/3-antiprisms). The then open faces could be closed by a complemental ring of 10 paps (5-antiprisms) – up to some "glue" of 50 tets: This is how gudap could be obtained herefrom as a subsymmetrical faceting.

If considered with according densities, then sishi can be thought of as the external blend of 120 sissidpies. This decomposition is described as the degenerate segmentoteron ox5/2oo5oo3oo&#x.

As abstract polytope both sishi and gaghi are equivalent to the amalgamation of {5,5}₆ with {5,3}, i.e. amal_s(abst.)^s(o3o5o5x).

Incidence matrix according to Dynkin symbol

x5/2o5o3o

.   . . . | 120 ♦   20 |  30 |  12
----------+-----+------+-----+----
x   . . . |   2 | 1200 |   3 |   3
----------+-----+------+-----+----
x5/2o . . |   5 |    5 | 720 |   2
----------+-----+------+-----+----
x5/2o5o . ♦  12 |   30 |  12 | 120

x5/2o5o3/2o

.   . .   . | 120 ♦   20 |  30 |  12
------------+-----+------+-----+----
x   . .   . |   2 | 1200 |   3 |   3
------------+-----+------+-----+----
x5/2o .   . |   5 |    5 | 720 |   2
------------+-----+------+-----+----
x5/2o5o   . ♦  12 |   30 |  12 | 120

x5/2o5/4o3o

.   .   . . | 120 ♦   20 |  30 |  12
------------+-----+------+-----+----
x   .   . . |   2 | 1200 |   3 |   3
------------+-----+------+-----+----
x5/2o   . . |   5 |    5 | 720 |   2
------------+-----+------+-----+----
x5/2o5/4o . ♦  12 |   30 |  12 | 120

x5/2o5/4o3/2o

.   .   .   . | 120 ♦   20 |  30 |  12
--------------+-----+------+-----+----
x   .   .   . |   2 | 1200 |   3 |   3
--------------+-----+------+-----+----
x5/2o   .   . |   5 |    5 | 720 |   2
--------------+-----+------+-----+----
x5/2o5/4o   . ♦  12 |   30 |  12 | 120

x5/3o5o3o

.   . . . | 120 ♦   20 |  30 |  12
----------+-----+------+-----+----
x   . . . |   2 | 1200 |   3 |   3
----------+-----+------+-----+----
x5/3o . . |   5 |    5 | 720 |   2
----------+-----+------+-----+----
x5/3o5o . ♦  12 |   30 |  12 | 120

x5/3o5o3/2o

.   . .   . | 120 ♦   20 |  30 |  12
------------+-----+------+-----+----
x   . .   . |   2 | 1200 |   3 |   3
------------+-----+------+-----+----
x5/3o .   . |   5 |    5 | 720 |   2
------------+-----+------+-----+----
x5/3o5o   . ♦  12 |   30 |  12 | 120

x5/3o5/4o3o

.   .   . . | 120 ♦   20 |  30 |  12
------------+-----+------+-----+----
x   .   . . |   2 | 1200 |   3 |   3
------------+-----+------+-----+----
x5/3o   . . |   5 |    5 | 720 |   2
------------+-----+------+-----+----
x5/3o5/4o . ♦  12 |   30 |  12 | 120

x5/3o5/4o3/2o

.   .   .   . | 120 ♦   20 |  30 |  12
--------------+-----+------+-----+----
x   .   .   . |   2 | 1200 |   3 |   3
--------------+-----+------+-----+----
x5/3o   .   . |   5 |    5 | 720 |   2
--------------+-----+------+-----+----
x5/3o5/4o   . ♦  12 |   30 |  12 | 120