Acronym fix, pI
Name icosahedral hecatonicosachoron,
faceted hexacosichoron,
polyicosahedron
Cross sections 
 ©
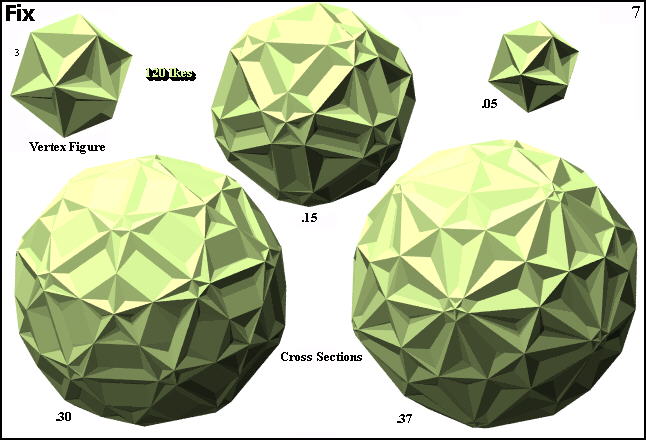Circumradius (1+sqrt(5))/2 = 1.618034
Inradius (3+sqrt(5))/4 = 1.309017
Density 4
Coordinates
  1. (τ, 0, 0, 0)             & all permutations, all changes of sign
    (vertex inscribed f/q-hex)
  2. (τ/2, τ/2, τ/2, τ/2)   & all permutations, all changes of sign
    (vertex inscribed f-tes)
  3. (τ2/2, τ/2, 1/2, 0)   & even permutations, all changes of sign
    (vertex inscribed sadi)
where τ = (1+sqrt(5))/2 (a. and b. together define a vertex inscribed f-ico)
General of army ex
Colonel of regiment ex
Dual sishi
Dihedral angles
  • at {3} between ike and ike:   120°
Face vector 120, 720, 1200, 120
Confer
Grünbaumian relatives:
ex+fix   2ex+fix   3ex+fix   3ex+2fix+gaghi   fix+gahi+120id   2fix  
segmentochora:
ikepy  
decompositions:
sishi || fix  
general polytopal classes:
Wythoffian polychora   regular   noble polytopes  
External
links 		hedrondude   wikipedia   polytopewiki   WikiChoron   nan ma

As abstract polytope fix is isomorphic to gofix, thereby replacing ike by gike, resp. replacing pentagrammal edge figures by pentagonal ones, resp. replacing gad vertex figures by sissid ones.

If considered with according densities, then fix can be thought of as the external blend of 1 sishi + 120 sissidpies + 720 stascs + 1200 pens + 120 ikepies. This decomposition is described as the degenerate segmentoteron xo5/2oo5oo3ox&#x.

Conversely fix itself is obtained from ex as a faceting, then introducing instead the latter's vertex figures. In fact the external blend of fix and 120 ikepies completes it back again. Btw., this construction also shows that the vertices of fix are exactly above its facets.


Incidence matrix according to Dynkin symbol

x3o5o5/2o

. . .   . | 120 ♦  12 |   30 |  12
----------+-----+-----+------+----
x . .   . |   2 | 720 |    5 |   5
----------+-----+-----+------+----
x3o .   . |   3 |   3 | 1200 |   2
----------+-----+-----+------+----
x3o5o   . ♦  12 |  30 |   20 | 120


x3o5o5/3o

. . .   . | 120 ♦  12 |   30 |  12
----------+-----+-----+------+----
x . .   . |   2 | 720 |    5 |   5
----------+-----+-----+------+----
x3o .   . |   3 |   3 | 1200 |   2
----------+-----+-----+------+----
x3o5o   . ♦  12 |  30 |   20 | 120


x3o5/4o5/2o

. .   .   . | 120 ♦  12 |   30 |  12
------------+-----+-----+------+----
x .   .   . |   2 | 720 |    5 |   5
------------+-----+-----+------+----
x3o   .   . |   3 |   3 | 1200 |   2
------------+-----+-----+------+----
x3o5/4o   . ♦  12 |  30 |   20 | 120


x3o5/4o5/3o

. .   .   . | 120 ♦  12 |   30 |  12
------------+-----+-----+------+----
x .   .   . |   2 | 720 |    5 |   5
------------+-----+-----+------+----
x3o   .   . |   3 |   3 | 1200 |   2
------------+-----+-----+------+----
x3o5/4o   . ♦  12 |  30 |   20 | 120


x3/2o5o5/2o

.   . .   . | 120 ♦  12 |   30 |  12
------------+-----+-----+------+----
x   . .   . |   2 | 720 |    5 |   5
------------+-----+-----+------+----
x3/2o .   . |   3 |   3 | 1200 |   2
------------+-----+-----+------+----
x3/2o5o   . ♦  12 |  30 |   20 | 120


x3/2o5o5/3o

.   . .   . | 120 ♦  12 |   30 |  12
------------+-----+-----+------+----
x   . .   . |   2 | 720 |    5 |   5
------------+-----+-----+------+----
x3/2o .   . |   3 |   3 | 1200 |   2
------------+-----+-----+------+----
x3/2o5o   . ♦  12 |  30 |   20 | 120


x3/2o5/4o5/2o

.   .   .   . | 120 ♦  12 |   30 |  12
--------------+-----+-----+------+----
x   .   .   . |   2 | 720 |    5 |   5
--------------+-----+-----+------+----
x3/2o   .   . |   3 |   3 | 1200 |   2
--------------+-----+-----+------+----
x3/2o5/4o   . ♦  12 |  30 |   20 | 120


x3/2o5/4o5/3o

.   .   .   . | 120 ♦  12 |   30 |  12
--------------+-----+-----+------+----
x   .   .   . |   2 | 720 |    5 |   5
--------------+-----+-----+------+----
x3/2o   .   . |   3 |   3 | 1200 |   2
--------------+-----+-----+------+----
x3/2o5/4o   . ♦  12 |  30 |   20 | 120

© 2004-2024
top of page