Acronym	gaghi, gapD
Name	great grand hecatonicosachoron, greatened aggrandized polydodecahedron
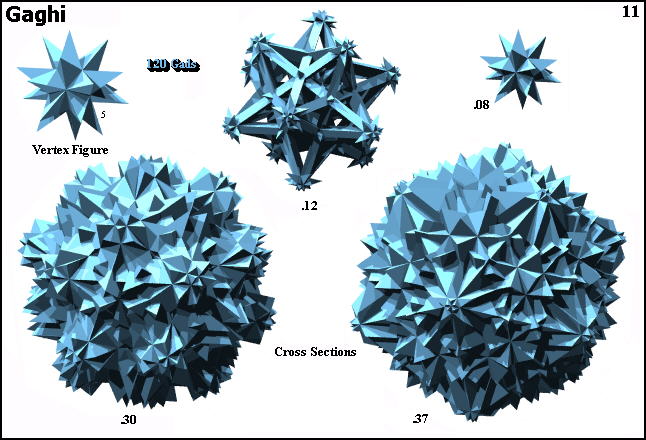
Cross sections	©
Circumradius	1
Inradius	(sqrt(5)-1)/4 = 0.309017
Density	76
Coordinates	(1, 0, 0, 0)                                         & all permutations, all changes of sign (vertex inscribed q-hex) (1/2, 1/2, 1/2, 1/2)                             & all permutations, all changes of sign (vertex inscribed tes) ((1+sqrt(5))/4, (sqrt(5)-1)/4, 1/4, 0)   & all even permutations, all changes of sign (vertex inscribed v-sadi)
General of army	ex
Colonel of regiment	sishi
Dual	gofix
Dihedral angles	at {5} between gad and gad:   72°
Face vector	120, 1200, 720, 120
Confer	Grünbaumian relatives: gaghi+didhi   gaghi+idhi   gaghi+paphacki+sridaphi   gaghi+sridixhi   2gaghi   2gaghi+2paphacki   sishi+gaghi+idhi   decompositions: pt || gaghi   general polytopal classes: Wythoffian polychora   regular   noble polytopes
External links

As abstract polytope gaghi is isomorphic to sishi, thereby replacing pentagons by pentagrams, resp. gad by sissid, resp. replacing gissid vertex figures by doe ones. – As such gaghi is a lieutenant.

If considered with according densities, then gaghi can be thought of as the external blend of 120 gadpies. This decomposition is described as the degenerate segmentoteron ox5oo5/2oo3oo&#x.

Incidence matrix according to Dynkin symbol

x5o5/2o3o

. .   . . | 120 ♦   20 |  30 |  12
----------+-----+------+-----+----
x .   . . |   2 | 1200 |   3 |   3
----------+-----+------+-----+----
x5o   . . |   5 |    5 | 720 |   2
----------+-----+------+-----+----
x5o5/2o . ♦  12 |   30 |  12 | 120

x5o5/2o3/2o

. .   .   . | 120 ♦   20 |  30 |  12
------------+-----+------+-----+----
x .   .   . |   2 | 1200 |   3 |   3
------------+-----+------+-----+----
x5o   .   . |   5 |    5 | 720 |   2
------------+-----+------+-----+----
x5o5/2o   . ♦  12 |   30 |  12 | 120

x5o5/3o3o

. .   . . | 120 ♦   20 |  30 |  12
----------+-----+------+-----+----
x .   . . |   2 | 1200 |   3 |   3
----------+-----+------+-----+----
x5o   . . |   5 |    5 | 720 |   2
----------+-----+------+-----+----
x5o5/3o . ♦  12 |   30 |  12 | 120

x5o5/3o3/2o

. .   .   . | 120 ♦   20 |  30 |  12
------------+-----+------+-----+----
x .   .   . |   2 | 1200 |   3 |   3
------------+-----+------+-----+----
x5o   .   . |   5 |    5 | 720 |   2
------------+-----+------+-----+----
x5o5/3o   . ♦  12 |   30 |  12 | 120

x5/4o5/2o3o

.   .   . . | 120 ♦   20 |  30 |  12
------------+-----+------+-----+----
x   .   . . |   2 | 1200 |   3 |   3
------------+-----+------+-----+----
x5/4o   . . |   5 |    5 | 720 |   2
------------+-----+------+-----+----
x5/4o5/2o . ♦  12 |   30 |  12 | 120

x5/4o5/2o3/2o

.   .   .   . | 120 ♦   20 |  30 |  12
--------------+-----+------+-----+----
x   .   .   . |   2 | 1200 |   3 |   3
--------------+-----+------+-----+----
x5/4o   .   . |   5 |    5 | 720 |   2
--------------+-----+------+-----+----
x5/4o5/2o   . ♦  12 |   30 |  12 | 120

x5/4o5/3o3o

.   .   . . | 120 ♦   20 |  30 |  12
------------+-----+------+-----+----
x   .   . . |   2 | 1200 |   3 |   3
------------+-----+------+-----+----
x5/4o   . . |   5 |    5 | 720 |   2
------------+-----+------+-----+----
x5/4o5/3o . ♦  12 |   30 |  12 | 120

x5/4o5/3o3/2o

.   .   .   . | 120 ♦   20 |  30 |  12
--------------+-----+------+-----+----
x   .   .   . |   2 | 1200 |   3 |   3
--------------+-----+------+-----+----
x5/4o   .   . |   5 |    5 | 720 |   2
--------------+-----+------+-----+----
x5/4o5/3o   . ♦  12 |   30 |  12 | 120