Acronym hi, pD (alt.: pidex)
Name hecatonicosachoron,
120-cell,
dodecacontachoron,
twelftychoron,
cosmochoron,
dodecaplex,
polydodecahedron,
hyperdodecahedron
 
© 
 ©
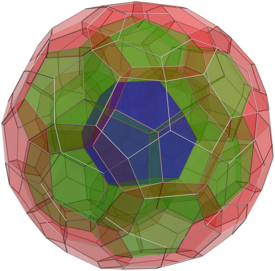
showing its relation
to swirl symmetry
Cross sections 
 ©
Circumradius sqrt[7+3 sqrt(5)] = 3.702459
Edge radius sqrt[27+12 sqrt(5)]/2 = 3.668542
Face radius sqrt[(65+29 sqrt(5))/10] = 3.603415
Inradius (7+3 sqrt(5))/4 = 3.427051
Density 1
Vertex figure 
 ©
Vertex layers
LayerSymmetrySubsymmetries
 o3o3o5o o3o3o . o3o . o o . o5o . o3o5o
1o3o3o5x o3o3o .
vertex first		 o3o . x
edge first		 o . o5x
{5} first		 . o3o5x
doe first
2 o3o3f .
vertex figure		 o3f . f f . o5f . o3o5f
3 o3f3x . o3F . o F . f5o . o3f5o
4a f3x3f . f3x . F x . o5F . f3x5o
4b B . x5o
5 F3f3o . f3F . o F . F5o . x3f5o
6 B3o3o . F3f . f f . f5f . f3o5f
7a x3f3F . B3o . x o . F5x . o3o5F
7b x3f . B C . f5o
8a f3o3B . x3B . o B . F5o . F3o5x
8b F3F3o . f3o . C
9a C3o3o . F3F . F F . x5F . o3o5F
9b o3o3C . o3o . D D . o5f
9c f3F3f .
10a o3B3x . f3F . B B . f5f . f3o5f
10b B3f3o .
11a F3o3B . f3B . f C . o5F . x3f5o
11b C3o . f o . f5F
12a F3f3F . o3B . B f . f5F . f3x5o
12b T . o5x
13a o3o3D . B3f . F o . B5o . o3f5o
13b B3x3f . o3C . F
13c F3o . D
14a f3o3C . D3o . o x . o5B . o3o5f
14b o3B3f . F3f . C B . F5x
15a f3F3F . o3o . T F . F5f . o3o5x
opposite doe
15b D . o5F
16a o3C3o . F3B . x f . B5o  
16b x3f3B . B3x . B T . o5f
16c B3f3x .
17a F3F3f . B3F . f C . f5f
17b f3o . T
18a C3o3f . C3f . o f . o5B
18b f3B3o . o3B . C T . f5o
19a D3o3o . o3D . F F . f5F
19b f3x3B . f3F . D D . F5o
20a F3f3F . f3C . f x . B5o
20b x3f . T B . x5F
21a B3o3F . B3f . B o . o5B
21b o3C . B
22a x3B3o . B3F . F f . F5f
22b o3f3B . T . x5o
23a o3o3C . x3D . o C . F5o
23b C3o3o . D3x . o o . F5f
23c f3F3f . F3F . C
24a B3o3f . F3B . F B . f5f
24b o3F3F .
25a F3f3x . f3B . B F . F5x
25b C3o . B D . f5o
26a o3o3B . C3f . f B . o5F
26b f3x . T
27a o3f3F . D3o . F o . x5F
27b F3f . D C . o5f
28a f3x3f . f3C . o f . f5f
28b B3o . C
29a x3f3o . F3B . f F . o5F
29b o3f . T
30a f3o3o . B3F . x x . F5o
30b x3B . B B . o5x
31 o3o3o .
opposite vertex		 o3o . T F . o5f
32a   o3D . o f . f5o
32b f3F . C
33a f3B . F o . x5o
opposite {5}
33b C3o . F
33c o3F . D
34 B3o . B  
35a B3f . f
35b o3C . f
36 F3f . B
37a F3F . F
37b o3o . D
38a B3x . o
38b o3f . C
39a o3B . x
39b f3x . B
40 f3F . f
41 F3f . o
42 x3f . F
43 F3o . o
44 f3o . f
45 o3o . x
opposite edge
(F=ff=f+x=2x+v, B=fff=F+f=2f+x=3x+2v, C=B+x=2F=2f+2x=4x+2v, D=C+v=3f+x=4x+3v, T=FF=3f+2x=5x+3v)
Lace city
in approx. ASCII-art 
 ©  

                                                  o5x                                                  
                                      o5f                     o5f                                      
                               f5o                                   f5o                               
                                                                                                       
                   x5o                     o5F           o5F                     x5o                   
                                                                                                       
                               F5o                                   F5o                               
                                      f5f                     f5f                                      
                                                                                                       
            f5o                                   F5x                                   f5o            
                   F5o                                                           F5o                   
                                                                                                       
       o5f                     x5F                                   x5F                     o5f       
                                                                                                       
                   f5f                                                           f5f                   
            o5F                                   F5f                                   o5F            
                                                                                                       
o5x                                   f5F                     f5F                                   o5x
                                                                                                       
                                                  B5o                                                  
                   F5x                     o5B           o5B                     F5x                   
                                                                                                       
       o5F                     F5f                                   F5f                     o5F       
o5f                                   B5o                     B5o                                   o5f
                                                                                                       
            f5f                                                                         f5f            
                                                                                                       
f5o                                   o5B                     o5B                                   f5o
       F5o                     f5F                                   f5F                     F5o       
                                                                                                       
                   x5F                     B5o           B5o                     x5F                   
                                                  o5B                                                  
                                                                                                       
x5o                                   F5f                     F5f                                   x5o
                                                                                                       
            F5o                                   f5F                                   F5o            
                   f5f                                                           f5f                   
                                                                                                       
       f5o                     F5x                                   F5x                     f5o       
                                                                                                       
                   o5F                                                           o5F                   
            o5f                                   x5F                                   o5f            
                                                                                                       
                                      f5f                     f5f                                      
                               o5F                                   o5F                               
                                                                                                       
                   o5x                     F5o           F5o                     o5x                   
                                                                                                       
                               o5f                                   o5f                               
                                      f5o                     f5o                                      
                                                  x5o                                                  

                                                                                                _ +--------------------------------------------- o3o3o
                                                                                            _ - _ +--------------------------------------------- f3o3o
                                                                                        _ - _ -   _ +------------------------------------------- x3f3o
                                                                                    _ - _ -   _ -      _ +-------------------------------------- f3x3f
                                                                                _ - _ -   _ -      _ -   _ +------------------------------------ o3f3F
                                                                            _ - _ -   _ -      _ -   _ - _ +------------------------------------ o3o3B
                                                                        _ - _ -   _ -      _ -   _ - _ -   _ +---------------------------------- F3f3x
                                                                    _ - _ -   _ -      _ -   _ - _ -   _ -       _ +---------------------------- B3o3f + o3F3F
                                                                _ - _ -   _ -      _ -   _ - _ -   _ -       _ -   _ +-------------------------- o3o3C + C3o3o + f3F3f
                                                            _ - _ -   _ -      _ -   _ - _ -   _ -       _ -   _ -       _ +-------------------- x3B3o + o3f3B
                                                        _ - _ -   _ -      _ -   _ - _ -   _ -       _ -   _ -       _ -   _ +------------------ B3o3F
                                                    _ - _ -   _ -      _ -   _ - _ -   _ -       _ -   _ -       _ -   _ - _ +------------------ F3f3F
                                                _ - _ -   _ -      _ -   _ - _ -   _ -       _ -   _ -       _ -   _ - _ -   _ +---------------- D3o3o + f3x3B
                                            _ - _ -   _ -      _ -   _ - _ -   _ -       _ -   _ -       _ -   _ - _ -   _ -       _ +---------- C3o3f + f3B3o
                                        _ - _ -   _ -      _ -   _ - _ -   _ -       _ -   _ -       _ -   _ - _ -   _ -       _ -   _ +-------- F3F3f
                                    _ - _ -   _ -      _ -   _ - _ -   _ -       _ -   _ -       _ -   _ - _ -   _ -       _ -   _ -       _ +-- o3C3o + x3f3B + B3f3o
                                _ - _ -   _ -      _ -   _ - _ -   _ -       _ -   _ -       _ -   _ - _ -   _ -       _ -   _ -       _ -

                        o3o o3f   f3x       x3f   f3o o3o                        		-- o3o5x
                                                                                 
                                                                                 
               o3o   o3F       F3f             f3F       F3o   o3o               		-- o3o5f
                                                                                 
             o3f       f3F   B3o       F3F       o3B   F3f       f3o             		-- o3f5o
                                                                                 
                                                                                 
          f3x   F3f B3o   x3B      fC3Bo Bo3fC      B3x   o3B f3F   x3f          		-- f3x5o
                                                                                 
                                                                                 
                                                                                 
                                                                                 
     x3f       F3F  fC3Bo      D3o   F3B B3F   o3D      Bo3fC  F3F       f3x     		-- x3f5o
                                                                                 
                                                                                 
  f3o   f3F      Bo3fC      F3B   C3f       f3C   B3F      fC3Bo      F3f   o3f  		-- f3o5f
                                                                                 
o3o       o3B             B3F                       F3B             B3o       o3o		-- o3o5F
                                                                                 
                                                                                 
   F3o F3f   B3x       o3D   f3C      xD3Dx      C3f   D3o       x3B   f3F o3F   		-- F3o5x
                                                                                 
                                                                                 
o3o       o3B             B3F                       F3B             B3o       o3o		-- o3o5F
                                                                                 
  f3o   f3F      Bo3fC      F3B   C3f       f3C   B3F      fC3Bo      F3f   o3f  		-- f3o5f
                                                                                 
                                                                                 
     x3f       F3F  fC3Bo      D3o   F3B B3F   o3D      Bo3fC  F3F       f3x     		-- x3f5o
                                                                                 
                                                                                 
                                                                                 
                                                                                 
          f3x   F3f B3o   x3B      fC3Bo Bo3fC      B3x   o3B f3F   x3f          		-- f3x5o
                                                                                 
                                                                                 
             o3f       f3F   B3o       F3F       o3B   F3f       f3o             		-- o3f5o
                                                                                 
               o3o   o3F       F3f             f3F       F3o   o3o               		-- o3o5f
                                                                                 
                                                                                 
                        o3o o3f   f3x       x3f   f3o o3o                        		-- o3o5x


 ©  

 ©  

                               o2x    f2f  F2o    x2F    F2o  f2f    o2x                               		-- o3o5x
                                                                                                       
                                                                                                       
                                                                                                       
                   o2f         F2F    B2o         f2B         B2o    F2F         o2f                   		-- o3o5f
                                                                                                       
            o2o    f2F         B2f    F2B        oC2Co        F2B    B2f         f2F    o2o            		-- o3f5o
                                                                                                       
                                                                                                       
                                                                                                       
       f2o  F2f   Bx2xB        f2C   Co2FD B2B    D2f    B2B Co2FD   f2C        Bx2xB   F2f  f2o       		-- f3x5o
                                                                                                       
                                                                                                       
                                                                                                       
                                                                                                       
x2o    F2F  f2B    C2f        FD2DF   B2C  o2T    T2x    o2T  B2C   FD2DF        C2f    f2B  F2F    x2o		-- x3f5o
                                                                                                       
                                                                                                       
                                                                                                       
f2f    o2B  B2F   FD2Co        C2B   fT2Tf        B2D        fT2Tf   C2B        FD2Co   B2F  o2B    f2f		-- f3o5f
                                                                                                       
o2F                B2B         T2o                F2T                T2o         B2B                o2F		-- o3o5F
                                                                                                       
                                                                                                       
                                                                                                       
F2x    B2f oC2Co   f2D         x2T    D2B  T2F    C2C    T2F  D2B    x2T         f2D   oC2Co B2f    F2x		-- F3o5x
                                                                                                       
                                                                                                       
                                                                                                       
o2F                B2B         T2o                F2T                T2o         B2B                o2F		-- o3o5F
                                                                                                       
f2f    o2B  B2F   FD2Co        C2B   fT2Tf        B2D        fT2Tf   C2B        FD2Co   B2F  o2B    f2f		-- f3o5f
                                                                                                       
                                                                                                       
                                                                                                       
x2o    F2F  f2B    C2f        FD2DF   B2C  o2T    T2x    o2T  B2C   FD2DF        C2f    f2B  F2F    x2o		-- x3f5o
                                                                                                       
                                                                                                       
                                                                                                       
                                                                                                       
       f2o  F2f   Bx2xB        f2C   Co2FD B2B    D2f    B2B Co2FD   f2C        Bx2xB   F2f  f2o       		-- f3x5o
                                                                                                       
                                                                                                       
                                                                                                       
            o2o    f2F         B2f    F2B        oC2Co        F2B    B2f         f2F    o2o            		-- o3f5o
                                                                                                       
                   o2f         F2F    B2o         f2B         B2o    F2F         o2f                   		-- o3o5f
                                                                                                       
                                                                                                       
                                                                                                       
                               o2x    f2f  F2o    x2F    F2o  f2f    o2x                               		-- o3o5x
Coordinates
  1. (τ2, τ2, 0, 0)                           all permutations, all changes of sign
  2. (sqrt(5) τ2/2, τ2/2, τ2/2, τ2/2) all permutations, all changes of sign
  3. (τ3/2, τ3/2, τ3/2, 1/2)              all permutations, all changes of sign
  4. (τ4/2, τ/2, τ/2, τ/2)                  all permutations, all changes of sign
  5. (τ4/2, τ2/2, 1/2, 0)                  all even permutations, all changes of sign
  6. (τ3/2, sqrt(5) τ2/2, 0, τ/2)       all even permutations, all changes of sign
  7. (τ3/2, τ2/2, τ2, τ/2)                 all even permutations, all changes of sign
where τ = (1+sqrt(5))/2
General of army (is itself convex)
Colonel of regiment (is itself locally convex – uniform polychoral members:
by cells: doe
hi 120
)
Volume (1575+705 sqrt(5))/4 = 787.856981
Surface 450+210 sqrt(5) = 919.574275
Dual ex
Dihedral angles
  • at {5} between doe and doe:   144°
Face vector 600, 1200, 720, 120
Confer
Grünbaumian relatives:
2hi   4hi  
decompositions:
rox || hi   hi - 120 ikadoes  
isogonal relatives:
hidhi  
ambification:
rahi  
general polytopal classes:
Wythoffian polychora   Catalan polychora   regular   noble polytopes  
External
links 		hedrondude   wikipedia   polytopewiki   WikiChoron   mathworld   quickfur   nan ma

As abstract polytope hi is isomorphic to gogishi, thereby replacing pentagons by pentagrams resp. replacing doe by gissid.

The 120 does could be divided into 12 cycles of 10, thus describing its swirl subsymmetry. Any 2 of those stacked does in such a ring are connected by special pentagons with a-type edges only. All non-polar pentagons of each doe belong to a second class. But there will be a chiral subset of 5 tropal edges of each doe, which is of that type too. And the other ones will belong to the former class, then. I.e. at that tropal edge there will be incident, as third pentagon, one such cycle dividing one again. That is, the non-polar pentagons would have the edge sequence a-b-a-b-b. Further it will turn out that those cycle dividing pentagons are completely separated from each other, i.e. there is incident just one such pentagon at any vertex of hi only.

Note that hi can be thought of as the external blend of 1 rox + 600 octpies + 1200 pens + 120 ikadoees. This decomposition is described as the degenerate segmentoteron oo3xo3oo5ox&#x.

The number of ways to color the hecatonicosachoron with different colors per cell is 120!/7200 = 9.290976 · 10194. – This is because the color group is the permutation group of 120 elements and has size 120!, while the order of the pure rotational hecatonicosachoral group is 7 200. (The reflectional hecatonicosachoral group would have twice as many, i.e. 14 400 elements.)

In the sense that bidex was found as the bi-icositetra-diminished ex and that a total of 5 (f-scaled) icos can be inscribed into ex, one might call sadi alternately "idex", the dual of bidex then becomes tridex, the dual of sadi becomes quidex, and the dual of ex itself, being this polytope, hi, could finally be dubbed "pidex" too.


Incidence matrix according to Dynkin symbol

o3o3o5x

. . . . | 600 ♦    4 |   6 |   4
--------+-----+------+-----+----
. . . x |   2 | 1200 |   3 |   3
--------+-----+------+-----+----
. . o5x |   5 |    5 | 720 |   2
--------+-----+------+-----+----
. o3o5x ♦  20 |   30 |  12 | 120

snubbed forms: o3o3o5β


o3o3o5/4x

. . .   . | 600 ♦    4 |   6 |   4
----------+-----+------+-----+----
. . .   x |   2 | 1200 |   3 |   3
----------+-----+------+-----+----
. . o5/4x |   5 |    5 | 720 |   2
----------+-----+------+-----+----
. o3o5/4x ♦  20 |   30 |  12 | 120


o3o3/2o5x

. .   . . | 600 ♦    4 |   6 |   4
----------+-----+------+-----+----
. .   . x |   2 | 1200 |   3 |   3
----------+-----+------+-----+----
. .   o5x |   5 |    5 | 720 |   2
----------+-----+------+-----+----
. o3/2o5x ♦  20 |   30 |  12 | 120


o3o3/2o5/4x

. .   .   . | 600 ♦    4 |   6 |   4
------------+-----+------+-----+----
. .   .   x |   2 | 1200 |   3 |   3
------------+-----+------+-----+----
. .   o5/4x |   5 |    5 | 720 |   2
------------+-----+------+-----+----
. o3/2o5/4x ♦  20 |   30 |  12 | 120


o3/2o3o5x

.   . . . | 600 ♦    4 |   6 |   4
----------+-----+------+-----+----
.   . . x |   2 | 1200 |   3 |   3
----------+-----+------+-----+----
.   . o5x |   5 |    5 | 720 |   2
----------+-----+------+-----+----
.   o3o5x ♦  20 |   30 |  12 | 120


o3/2o3o5/4x

.   . .   . | 600 ♦    4 |   6 |   4
------------+-----+------+-----+----
.   . .   x |   2 | 1200 |   3 |   3
------------+-----+------+-----+----
.   . o5/4x |   5 |    5 | 720 |   2
------------+-----+------+-----+----
.   o3o5/4x ♦  20 |   30 |  12 | 120


o3/2o3/2o5x

.   .   . . | 600 ♦    4 |   6 |   4
------------+-----+------+-----+----
.   .   . x |   2 | 1200 |   3 |   3
------------+-----+------+-----+----
.   .   o5x |   5 |    5 | 720 |   2
------------+-----+------+-----+----
.   o3/2o5x ♦  20 |   30 |  12 | 120


o3/2o3/2o5/4x

.   .   .   . | 600 ♦    4 |   6 |   4
--------------+-----+------+-----+----
.   .   .   x |   2 | 1200 |   3 |   3
--------------+-----+------+-----+----
.   .   o5/4x |   5 |    5 | 720 |   2
--------------+-----+------+-----+----
.   o3/2o5/4x ♦  20 |   30 |  12 | 120


acc. to swirl subsymmetry:

 600 ♦   2   2 |   1   5 |   4
-----+---------+---------+----
   2 | 600   * |   1   2 |   3  a
   2 |   * 600 |   0   3 |   3  b
-----+---------+---------+----
   5 |   5   0 | 120   * |   2  aaaaa
   5 |   2   3 |   * 600 |   2  ababb
-----+---------+---------+----
♦ 20 |  15  15 |   2  10 | 120


((xofoFo|f|FxFfBo-5-oxofoF|f|xFfFoB-2-BoFfFx|f|oFofox-5-oBfFxF|f|Fofoxo))&#zx   → existing heights = 0
                                                                                  B = 2f+x = 4.236068
                                                                                  F = f+x = 2.618034

o..... . ...... 5 o..... . ...... 2 o..... . ...... 5 o..... . ......      & | 100   *   *   * ♦   2   2   0   0   0   0 |  1   4   1   0   0 |  2   2
..o... . ...... 5 ..o... . ...... 2 ..o... . ...... 5 ..o... . ......      & |   * 200   *   * ♦   0   1   2   1   0   0 |  0   3   1   2   0 |  1   3
....o. . ...... 5 ....o. . ...... 2 ....o. . ...... 5 ....o. . ......      & |   *   * 200   * ♦   0   0   0   1   1   2 |  0   0   1   2   3 |  0   4
...... o ...... 5 ...... o ...... 2 ...... o ...... 5 ...... o ......        |   *   *   * 100 ♦   0   0   0   0   0   4 |  0   0   0   2   4 |  0   4
-----------------------------------------------------------------------------+-----------------+-------------------------+--------------------+-------
x..... . ......   ...... . ......   ...... . ......   ...... . ......      & |   2   0   0   0 | 100   *   *   *   *   * |  1   2   0   0   0 |  2   1
o.o... . ...... 5 o.o... . ...... 2 o.o... . ...... 5 o.o... . ......&#x   & |   1   1   0   0 |   * 200   *   *   *   * |  0   2   1   0   0 |  1   2
..oo.. . ...... 5 ..oo.. . ...... 2 ..oo.. . ...... 5 ..oo.. . ......&#x   & |   0   2   0   0 |   *   * 200   *   *   * |  0   2   0   1   0 |  1   2
..o.o. . ...... 5 ..o.o. . ...... 2 ..o.o. . ...... 5 ..o.o. . ......&#x   & |   0   1   1   0 |   *   *   * 200   *   * |  0   0   1   2   0 |  0   3
...... . ......   ...... . ......   ...... . ......   ....x. . ......      & |   0   0   2   0 |   *   *   *   * 100   * |  0   0   1   0   2 |  0   3
....o. o ...... 5 ....o. o ...... 2 ....o. o ...... 5 ....o. o ......&#x   & |   0   0   1   1 |   *   *   *   *   * 400 |  0   0   0   1   2 |  0   3
-----------------------------------------------------------------------------+-----------------+-------------------------+--------------------+-------
x..... . ...... 5 o..... . ......   ...... . ......   ...... . ......      & |   5   0   0   0 |   5   0   0   0   0   0 | 20   *   *   *   * |  2   0
x.fo.. . ......   ...... . ......   ...... . ......   ...... . ......&#xt  & |   2   3   0   0 |   1   2   2   0   0   0 |  * 200   *   *   * |  1   1
...... . ......   ...... . ......   ...... . ......   o.f.x. . ......&#xt  & |   1   2   2   0 |   0   2   0   2   1   0 |  *   * 100   *   * |  0   2
..oooo o ...... 5 ..oooo o ...... 2 ..oooo o ...... 5 ..oooo o ......&#xr  & |   0   2   2   1 |   0   0   1   2   0   2 |  *   *   * 200   * |  0   2
...... . ......   ...... . ......   ...... . ......   ....x. f .o....&#xt  & |   0   0   3   2 |   0   0   0   0   1   4 |  *   *   *   * 200 |  0   2
-----------------------------------------------------------------------------+-----------------+-------------------------+--------------------+-------
xofo.. . ...... 5 oxof.. . ......   ...... . ......   ...... . ......&#xt  & ♦  10  10   0   0 |  10  10  10   0   0   0 |  2  10   0   0   0 | 20   *  tower: a-c-d-b
x.foFo f .x....   ...... . ......   ...... . ......   o.fFxF f .o....&#xt  & ♦   2   6   8   4 |   1   4   4   6   3  12 |  0   2   2   4   4 |  * 100


((ooC|foB|xoF|f-3-ooo|ooo|fff|x-3-Coo|Bfo|Fxo|f *b3-oCo|oBf|oFx|f))&#zx   → existing heights = 0
                                                                            C = 2f+2x = 5.236068
                                                                            B = 2f+x = 4.236068
                                                                            F = f+x = 2.618034
(tegum sum of 3 C-hexes, 3 (f,B)-rits, 3 (x,f,F)-tahs, and 1 (f,x)-tico)

  o.. ... ... .-3-o.. ... ... .-3-o.. ... ... . *b3-o.. ... ... .        | 8 * *  *  *  *  *  *  *   * ♦  4  0  0  0  0  0  0   0  0   0  0   0  0 |  6  0  0  0  0  0  0  0  0 |  4  0  0  0
  .o. ... ... .-3-.o. ... ... .-3-.o. ... ... . *b3-.o. ... ... .        | * 8 *  *  *  *  *  *  *   * ♦  0  4  0  0  0  0  0   0  0   0  0   0  0 |  0  6  0  0  0  0  0  0  0 |  0  4  0  0
  ..o ... ... .-3-..o ... ... .-3-..o ... ... . *b3-..o ... ... .        | * * 8  *  *  *  *  *  *   * ♦  0  0  4  0  0  0  0   0  0   0  0   0  0 |  0  0  6  0  0  0  0  0  0 |  0  0  4  0
  ... o.. ... .-3-... o.. ... .-3-... o.. ... . *b3-... o.. ... .        | * * * 32  *  *  *  *  *   * ♦  1  0  0  3  0  0  0   0  0   0  0   0  0 |  3  0  0  3  0  0  0  0  0 |  3  0  1  0
  ... .o. ... .-3-... .o. ... .-3-... .o. ... . *b3-... .o. ... .        | * * *  * 32  *  *  *  *   * ♦  0  1  0  0  3  0  0   0  0   0  0   0  0 |  0  3  0  0  3  0  0  0  0 |  1  3  0  0
  ... ..o ... .-3-... ..o ... .-3-... ..o ... . *b3-... ..o ... .        | * * *  *  * 32  *  *  *   * ♦  0  0  1  0  0  3  0   0  0   0  0   0  0 |  0  0  3  0  0  3  0  0  0 |  0  1  3  0
  ... ... o.. .-3-... ... o.. .-3-... ... o.. . *b3-... ... o.. .        | * * *  *  *  * 96  *  *   * ♦  0  0  0  1  0  0  1   2  0   0  0   0  0 |  1  0  0  2  0  0  2  1  0 |  2  0  1  1
  ... ... .o. .-3-... ... .o. .-3-... ... .o. . *b3-... ... .o. .        | * * *  *  *  *  * 96  *   * ♦  0  0  0  0  1  0  0   0  1   2  0   0  0 |  0  1  0  0  2  0  1  0  2 |  1  2  0  1
  ... ... ..o .-3-... ... ..o .-3-... ... ..o . *b3-... ... ..o .        | * * *  *  *  *  *  * 96   * ♦  0  0  0  0  0  1  0   0  0   0  1   2  0 |  0  0  1  0  0  2  0  2  1 |  0  1  2  1
  ... ... ... o-3-... ... ... o-3-... ... ... o *b3-... ... ... o        | * * *  *  *  *  *  *  * 192 ♦  0  0  0  0  0  0  0   1  0   1  0   1  1 |  0  0  0  1  1  1  1  1  1 |  1  1  1  1
-------------------------------------------------------------------------+-----------------------------+-------------------------------------------+----------------------------+------------
  o.. o.. ... .-3-o.. o.. ... .-3-o.. o.. ... . *b3-o.. o.. ... .  &#x   | 1 0 0  1  0  0  0  0  0   0 | 32  *  *  *  *  *  *   *  *   *  *   *  * |  3  0  0  0  0  0  0  0  0 |  3  0  0  0
  .o. .o. ... .-3-.o. .o. ... .-3-.o. .o. ... . *b3-.o. .o. ... .  &#x   | 0 1 0  0  1  0  0  0  0   0 |  * 32  *  *  *  *  *   *  *   *  *   *  * |  0  3  0  0  0  0  0  0  0 |  0  3  0  0
  ..o ..o ... .-3-..o ..o ... .-3-..o ..o ... . *b3-..o ..o ... .  &#x   | 0 0 1  0  0  1  0  0  0   0 |  *  * 32  *  *  *  *   *  *   *  *   *  * |  0  0  3  0  0  0  0  0  0 |  0  0  3  0
  ... o.. o.. .-3-... o.. o.. .-3-... o.. o.. . *b3-... o.. o.. .  &#x   | 0 0 0  1  0  0  1  0  0   0 |  *  *  * 96  *  *  *   *  *   *  *   *  * |  1  0  0  2  0  0  0  0  0 |  2  0  1  0
  ... .o. .o. .-3-... .o. .o. .-3-... .o. .o. . *b3-... .o. .o. .  &#x   | 0 0 0  0  1  0  0  1  0   0 |  *  *  *  * 96  *  *   *  *   *  *   *  * |  0  1  0  0  2  0  0  0  0 |  1  2  0  0
  ... ..o ..o .-3-... ..o ..o .-3-... ..o ..o . *b3-... ..o ..o .  &#x   | 0 0 0  0  0  1  0  0  1   0 |  *  *  *  *  * 96  *   *  *   *  *   *  * |  0  0  1  0  0  2  0  0  0 |  0  1  2  0
  ... ... x.. .   ... ... ... .   ... ... ... .     ... ... ... .        | 0 0 0  0  0  0  2  0  0   0 |  *  *  *  *  *  * 48   *  *   *  *   *  * |  1  0  0  0  0  0  2  0  0 |  2  0  0  1
  ... ... o.. o-3-... ... o.. o-3-... ... o.. o *b3-... ... o.. o  &#x   | 0 0 0  0  0  0  1  0  0   1 |  *  *  *  *  *  *  * 192  *   *  *   *  * |  0  0  0  1  0  0  1  1  0 |  1  0  1  1
  ... ... ... .   ... ... ... .   ... ... .x. .     ... ... ... .        | 0 0 0  0  0  0  0  2  0   0 |  *  *  *  *  *  *  *   * 48   *  *   *  * |  0  1  0  0  0  0  0  0  2 |  0  2  0  1
  ... ... .o. o-3-... ... .o. o-3-... ... .o. o *b3-... ... .o. o  &#x   | 0 0 0  0  0  0  0  1  0   1 |  *  *  *  *  *  *  *   *  * 192  *   *  * |  0  0  0  0  1  0  1  0  1 |  1  1  0  1
  ... ... ... .   ... ... ... .   ... ... ... .     ... ... ..x .        | 0 0 0  0  0  0  0  0  2   0 |  *  *  *  *  *  *  *   *  *   * 48   *  * |  0  0  1  0  0  0  0  2  0 |  0  0  2  1
  ... ... ..o o-3-... ... ..o o-3-... ... ..o o *b3-... ... ..o o  &#x   | 0 0 0  0  0  0  0  0  1   1 |  *  *  *  *  *  *  *   *  *   *  * 192  * |  0  0  0  0  0  1  0  1  1 |  0  1  1  1
  ... ... ... .   ... ... ... x   ... ... ... .     ... ... ... .        | 0 0 0  0  0  0  0  0  0   2 |  *  *  *  *  *  *  *   *  *   *  *   * 96 |  0  0  0  1  1  1  0  0  0 |  1  1  1  0
-------------------------------------------------------------------------+-----------------------------+-------------------------------------------+----------------------------+------------
  o.. f.. x.. .   ... ... ... .   ... ... ... .     ... ... ... .  &#xt  | 1 0 0  2  0  0  2  0  0   0 |  2  0  0  2  0  0  1   0  0   0  0   0  0 | 48  *  *  *  *  *  *  *  * |  2  0  0  0
  ... ... ... .   ... ... ... .   .o. .f. .x. .     ... ... ... .  &#xt  | 0 1 0  0  2  0  0  2  0   0 |  0  2  0  0  2  0  0   0  1   0  0   0  0 |  * 48  *  *  *  *  *  *  * |  0  2  0  0
  ... ... ... .   ... ... ... .   ... ... ... .     ..o ..f ..x .  &#xt  | 0 0 1  0  0  2  0  0  2   0 |  0  0  2  0  0  2  0   0  0   0  1   0  0 |  *  * 48  *  *  *  *  *  * |  0  0  2  0
  ... ... ... .   ... o.. f.. x   ... ... ... .     ... ... ... .  &#xt  | 0 0 0  1  0  0  2  0  0   2 |  0  0  0  2  0  0  0   2  0   0  0   0  1 |  *  *  * 96  *  *  *  *  * |  1  0  1  0
  ... ... ... .   ... .o. .f. x   ... ... ... .     ... ... ... .  &#xt  | 0 0 0  0  1  0  0  2  0   2 |  0  0  0  0  2  0  0   0  0   2  0   0  1 |  *  *  *  * 96  *  *  *  * |  1  1  0  0
  ... ... ... .   ... ..o ..f x   ... ... ... .     ... ... ... .  &#xt  | 0 0 0  0  0  1  0  0  2   2 |  0  0  0  0  0  2  0   0  0   0  0   2  1 |  *  *  *  *  * 96  *  *  * |  0  1  1  0
  ... ... xo. f   ... ... ... .   ... ... ... .     ... ... ... .  &#xt  | 0 0 0  0  0  0  2  1  0   2 |  0  0  0  0  0  0  1   2  0   2  0   0  0 |  *  *  *  *  *  * 96  *  * |  1  0  0  1  tower g-j-h
  ... ... ... .   ... ... ... .   ... ... ... .     ... ... o.x f  &#xt  | 0 0 0  0  0  0  1  0  2   2 |  0  0  0  0  0  0  0   2  0   0  1   2  0 |  *  *  *  *  *  *  * 96  * |  0  0  1  1  tower g-j-i
  ... ... ... .   ... ... ... .   ... ... .xo f     ... ... ... .  &#xt  | 0 0 0  0  0  0  0  2  1   2 |  0  0  0  0  0  0  0   0  1   2  0   2  0 |  *  *  *  *  *  *  *  * 96 |  0  1  0  1  tower h-j-i
-------------------------------------------------------------------------+-----------------------------+-------------------------------------------+----------------------------+------------
  o.. fo. xo. f-3-o.. oo. ff. x   ... ... ... .     ... ... ... .  &#xt  ♦ 1 0 0  3  1  0  6  3  0   6 |  3  0  0  6  3  0  3   6  0   6  0   0  3 |  3  0  0  3  3  0  3  0  0 | 32  *  *  *  tower a-d-g-j-h-e
  ... ... ... .   .o. .oo .ff x-3-.o. .fo .xo f     ... ... ... .  &#xt  ♦ 0 1 0  0  3  1  0  6  3   6 |  0  3  0  0  6  3  0   0  3   6  0   6  3 |  0  3  0  0  3  3  0  0  3 |  * 32  *  *  tower b-e-h-j-i-f
  ... ... ... .   ..o o.o f.f x   ... ... ... . *b3-..o o.f o.x f  &#xt  ♦ 0 0 1  1  0  3  3  0  6   6 |  0  0  3  3  0  6  0   6  0   0  3   6  3 |  0  0  3  3  0  3  0  3  0 |  *  * 32  *  tower c-f-i-j-g-d
((... ... xoF f   ... ... ... .   ... ... Fxo f     ... ... oFx f))&#zx  ♦ 0 0 0  0  0  0  4  4  4   8 |  0  0  0  0  0  0  2   8  2   8  2   8  0 |  0  0  0  0  0  0  4  4  4 |  *  *  * 24

© 2004-2026
top of page