Acronym	tico
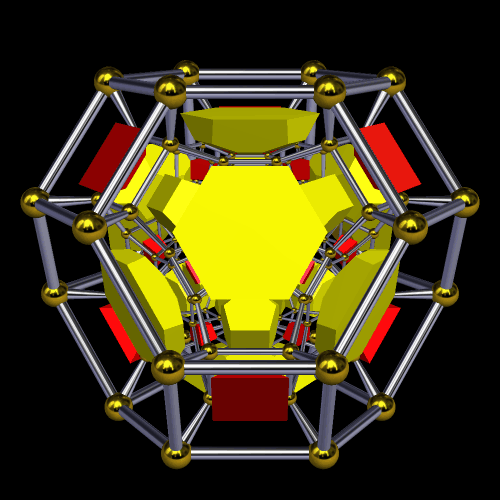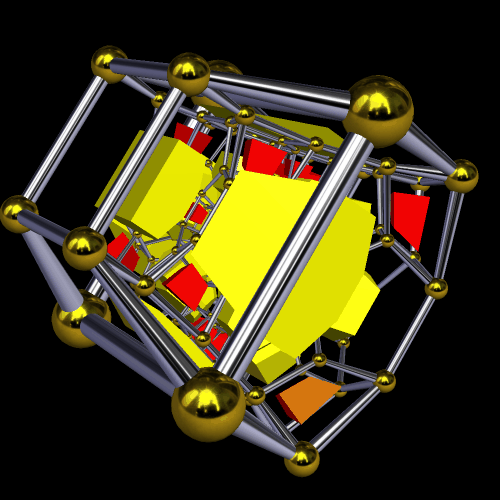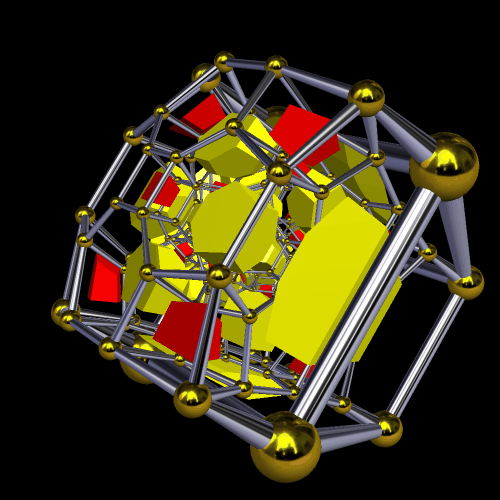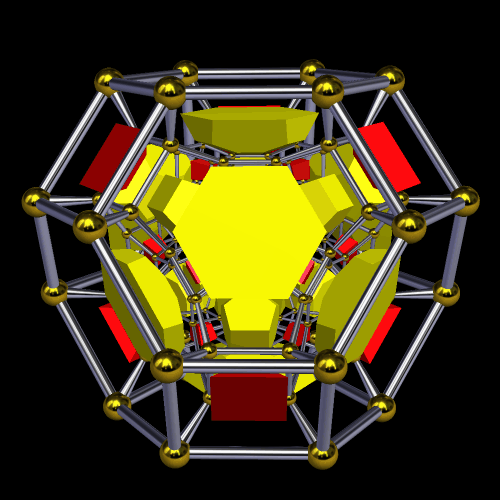
Name	truncated icositetrachoron, cantitruncated hexadecachoron
	©   ©
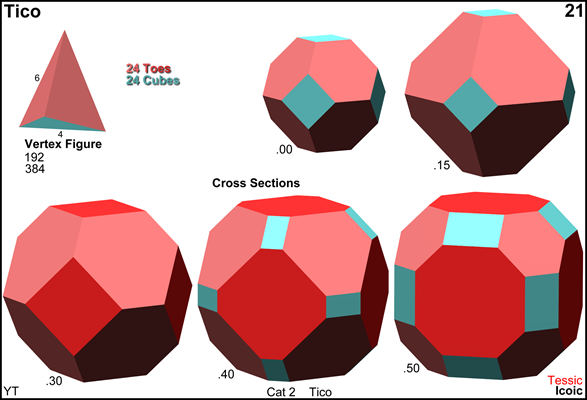
Cross sections	©
Circumradius	sqrt(7) = 2.645751
Vertex figure	©
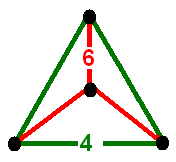Vertex layers	Layer Symmetry Subsymmetries   o3o4o3o o3o4o . o3o . o o . o3o . o4o3o 1 x3x4o3o x3x4o . toe first x3x . o {6} first x . o3o edge first . x4o3o cube first 2 u3x4o . x3u . q u . q3o . u4o3o 3a x3u4o . u3x . Q x . Q3o . x4q3o 3b x3d . o d . o3q 4 x3x4q . x3x . c b . o3o . u4o3q 5a x3u4o . d3x . Q x . Q3q . x4o3Q 5b u3d . o d . o3Q . d4o3o 6a u3x4o . u3x . c u . q3Q . x4o3Q 6b d3u . q . d4o3o 7a x3x4o . opposite toe b3u . o x . H3H . u4o3q 7b u3b . o e . o3o 8a   x3u . c b . o3Q . x4q3o 8b u3d . q 9a x3d . Q d . q3Q . u4o3o 9b d3u . o e . o3q 10 x3x . c u . H3H . x4o3o opposite cube 11a x3u . Q d . Q3q   11b d3x . o e . q3o 12 u3x . q b . Q3o 13a x3x . o opposite {6} x . H3H 13b e . o3o 14   u . Q3q 15a x . q3Q 15b d . Q3o 16 b . o3o 17a x . o3Q 17b d . q3o 18 u . o3q 19 x . o3o opposite edge   o3o3o4o o3o3o . o3o . o o . o4o . o3o4o 1 x3x3x4o x3x3x . toe first x3x . o {6} first x . x4o cube first . x3x4o toe first 2 x3u3x . x3u . q u . u4o . u3x4o 3a u3x3u . u3x . Q d . x4q . x3u4o 3b x3d . o x . d4o 4a x3x3d . x3x . c x . u4q . x3x4q 4b d3x3x . b . u4o 5a u3x3u . d3x . Q e . x4o . x3u4o 5b u3d . o d . d4o 5c x . x4Q 6a x3u3x . u3x . c e . x4o . u3x4o 6b d3u . q d . d4o 6c x . x4Q 7a x3x3x . opposite toe b3u . o x . u4q . x3x4o opposite toe 7b u3b . o b . u4o 8a   x3u . c d . x4q   8b u3d . q x . d4o 9a x3d . Q u . u4o 9b d3u . o 10 x3x . c x . x4o opposite cube 11a x3u . Q   11b d3x . o 12 u3x . q 13 x3x . o opposite {6}   o3o3o *b3o o3o3o    . o3o . *b3o o . o    o . o3o *b3o 1 x3x3x *b3x x3x3x    . toe first x3x . *b3x toe first x . x    x cube first . x3x *b3x toe first 2 x3u3x    . x3u . *b3x u . u    u . u3x *b3x 3a u3x3u    . u3x . *b3u x . d    d . x3u *b3u 3b d . x    d 3c d . d    x 4a x3x3d    . x3x . *b3d b . u    u . x3x *b3d 4b d3x3x    . d3x . *b3x u . b    u . x3d *b3x 4c u . u    b 5a u3x3u    . u3x . *b3u d . d    d . x3u *b3u 5b e . x    x 5c x . e    x 5d x . x    e 6a x3u3x    . x3u . *b3x d . d    d . u3x *b3x 6b e . x    x 6c x . e    x 6d x . x    e 7a x3x3x    . opposite toe x3x . *b3x opposite toe b . u    u . x3x *b3x opposite toe 7b u . b    u 7c u . u    b 8a     x . d    d   8b d . x    d 8c d . d    x 9 u . u    u 10 x . x    x opposite cube (d=3x, Q=2q, b=4x, c=3q, e=5x, H=hq)
Lace city in approx. ASCII-art	©   x4o u4o x4q u4o x4o x4o d4o u4q d4o x4o u4o d4o x4Q d4o u4o x4q u4q x4Q x4Q u4q x4q u4o d4o x4Q d4o u4o x4o d4o u4q d4o x4o x4o u4o x4q u4o x4o
	©   x3x x3u x3u u3x x3d u3x x3x x3x d3x u3d d3x u3x d3u d3u u3x bu3ub x3u u3d u3d x3u x3d d3u x3d x3x x3x x3u d3x x3u u3x u3x x3x
	©   o3o o3o o3q o3q q3o o3Q o3Q q3o o3o o3o Q3o q3Q q3Q Q3o Q3q Q3q o3o H3H H3H o3o Q3o Q3o q3o Q3q Q3q q3o H3H H3H o3q q3Q q3Q o3q o3Q o3Q o3o H3H H3H o3o q3Q q3Q o3Q Q3q Q3q o3Q o3o o3o o3q Q3o Q3o o3q q3o q3o o3o o3o
Coordinates	(3/sqrt(2), sqrt(2), 1/sqrt(2), 0)   & all permutations, all changes of sign or wrt. dual positioning of underlying ico: (5/2, 1/2, 1/2, 1/2)   & all permutations, all changes of sign (inscribed o3o3q4x) (3/2, 3/2, 3/2, 1/2)   & all permutations, all changes of sign (inscribed q3o3o4u) (2, 1, 1, 1)               & all permutations, all changes of sign (inscribed Q3o3o4x)
General of army	(is itself convex)
Colonel of regiment	(is itself locally convex – uniform polychoral members: by cells: cube toe tico 24 24 )
Dihedral angles	at {4} between cube and toe:   135° at {6} between toe and toe:   120°
Face vector	192, 384, 240, 48
Confer	compounds: tastic   tidox   decompositions: rico || tico   diminishings: oditico   general polytopal classes: Wythoffian polychora   lace simplices   partial Stott expansions
External links

Note that tico can be thought of as the external blend of 1 rico + 24 coatoes + 24 teses. This decomposition is described as the degenerate segmentoteron ox3xx4oo3oo&#x.

Incidence matrix according to Dynkin symbol

x3x4o3o

. . . . | 192 ♦  1   3 |  3   3 |  3  1
--------+-----+--------+--------+------
x . . . |   2 | 96   * |  3   0 |  3  0
. x . . |   2 |  * 288 |  1   2 |  2  1
--------+-----+--------+--------+------
x3x . . |   6 |  3   3 | 96   * |  2  0
. x4o . |   4 |  0   4 |  * 144 |  1  1
--------+-----+--------+--------+------
x3x4o . ♦  24 | 12  24 |  8   6 | 24  *
. x4o3o ♦   8 |  0  12 |  0   6 |  * 24

snubbed forms: β3x4o3o, x3β4o3o, s3s4o3o, s3s4o3o (faceting only), β3β4o3o

x3x4o3/2o

. . .   . | 192 ♦  1   3 |  3   3 |  3  1
----------+-----+--------+--------+------
x . .   . |   2 | 96   * |  3   0 |  3  0
. x .   . |   2 |  * 288 |  1   2 |  2  1
----------+-----+--------+--------+------
x3x .   . |   6 |  3   3 | 96   * |  2  0
. x4o   . |   4 |  0   4 |  * 144 |  1  1
----------+-----+--------+--------+------
x3x4o   . ♦  24 | 12  24 |  8   6 | 24  *
. x4o3/2o ♦   8 |  0  12 |  0   6 |  * 24

x3x4/3o3o

. .   . . | 192 ♦  1   3 |  3   3 |  3  1
----------+-----+--------+--------+------
x .   . . |   2 | 96   * |  3   0 |  3  0
. x   . . |   2 |  * 288 |  1   2 |  2  1
----------+-----+--------+--------+------
x3x   . . |   6 |  3   3 | 96   * |  2  0
. x4/3o . |   4 |  0   4 |  * 144 |  1  1
----------+-----+--------+--------+------
x3x4/3o . ♦  24 | 12  24 |  8   6 | 24  *
. x4/3o3o ♦   8 |  0  12 |  0   6 |  * 24

x3x4/3o3/2o

. .   .   . | 192 ♦  1   3 |  3   3 |  3  1
------------+-----+--------+--------+------
x .   .   . |   2 | 96   * |  3   0 |  3  0
. x   .   . |   2 |  * 288 |  1   2 |  2  1
------------+-----+--------+--------+------
x3x   .   . |   6 |  3   3 | 96   * |  2  0
. x4/3o   . |   4 |  0   4 |  * 144 |  1  1
------------+-----+--------+--------+------
x3x4/3o   . ♦  24 | 12  24 |  8   6 | 24  *
. x4/3o3/2o ♦   8 |  0  12 |  0   6 |  * 24

x3x3x4o

. . . . | 192 ♦  1  1   2 |  1  2  2  1 |  2  1 1
--------+-----+-----------+-------------+--------
x . . . |   2 | 96  *   * |  1  2  0  0 |  2  1 0
. x . . |   2 |  * 96   * |  1  0  2  0 |  2  0 1
. . x . |   2 |  *  * 192 |  0  1  1  1 |  1  1 1
--------+-----+-----------+-------------+--------
x3x . . |   6 |  3  3   0 | 32  *  *  * |  2  0 0
x . x . |   4 |  2  0   2 |  * 96  *  * |  1  1 0
. x3x . |   6 |  0  3   3 |  *  * 64  * |  1  0 1
. . x4o |   4 |  0  0   4 |  *  *  * 48 |  0  1 1
--------+-----+-----------+-------------+--------
x3x3x . ♦  24 | 12 12  12 |  4  6  4  0 | 16  * *
x . x4o ♦   8 |  4  0   8 |  0  4  0  2 |  * 24 *
. x3x4o ♦  24 |  0 12  24 |  0  0  8  6 |  *  * 8

snubbed forms: β3x3x4o, x3β3x4o, x3x3β4o, β3β3x4o, β3x3β4o, x3β3β4o, s3s3s4o, s3s3s4o (faceting only)

x3x3x4/3o

. . .   . | 192 ♦  1  1   2 |  1  2  2  1 |  2  1 1
----------+-----+-----------+-------------+--------
x . .   . |   2 | 96  *   * |  1  2  0  0 |  2  1 0
. x .   . |   2 |  * 96   * |  1  0  2  0 |  2  0 1
. . x   . |   2 |  *  * 192 |  0  1  1  1 |  1  1 1
----------+-----+-----------+-------------+--------
x3x .   . |   6 |  3  3   0 | 32  *  *  * |  2  0 0
x . x   . |   4 |  2  0   2 |  * 96  *  * |  1  1 0
. x3x   . |   6 |  0  3   3 |  *  * 64  * |  1  0 1
. . x4/3o |   4 |  0  0   4 |  *  *  * 48 |  0  1 1
----------+-----+-----------+-------------+--------
x3x3x   . ♦  24 | 12 12  12 |  4  6  4  0 | 16  * *
x . x4/3o ♦   8 |  4  0   8 |  0  4  0  2 |  * 24 *
. x3x4/3o ♦  24 |  0 12  24 |  0  0  8  6 |  *  * 8

x3x3x *b3x

. . .    . | 192 ♦  1  1  1  1 |  1  1  1  1  1  1 | 1 1  1 1
-----------+-----+-------------+-------------------+---------
x . .    . |   2 | 96  *  *  * |  1  1  1  0  0  0 | 1 1  1 0
. x .    . |   2 |  * 96  *  * |  1  0  0  1  1  0 | 1 1  0 1
. . x    . |   2 |  *  * 96  * |  0  1  0  1  0  1 | 1 0  1 1
. . .    x |   2 |  *  *  * 96 |  0  0  1  0  1  1 | 0 1  1 1
-----------+-----+-------------+-------------------+---------
x3x .    . |   6 |  3  3  0  0 | 32  *  *  *  *  * | 1 1  0 0
x . x    . |   4 |  2  0  2  0 |  * 48  *  *  *  * | 1 0  1 0
x . .    x |   4 |  2  0  0  2 |  *  * 48  *  *  * | 0 1  1 0
. x3x    . |   6 |  0  3  3  0 |  *  *  * 32  *  * | 1 0  0 1
. x . *b3x |   6 |  0  3  0  3 |  *  *  *  * 32  * | 0 1  0 1
. . x    x |   4 |  0  0  2  2 |  *  *  *  *  * 48 | 0 0  1 1
-----------+-----+-------------+-------------------+---------
x3x3x    . ♦  24 | 12 12 12  0 |  4  6  0  4  0  0 | 8 *  * *
x3x . *b3x ♦  24 | 12 12  0 12 |  4  0  6  0  4  0 | * 8  * *
x . x    x ♦   8 |  4  0  4  4 |  0  2  2  0  0  2 | * * 24 *
. x3x *b3x ♦  24 |  0 12 12 12 |  0  0  0  4  4  6 | * *  * 8

snubbed forms: β3x3x *b3x, x3β3x *b3x, β3β3x *b3x, β3x3β *b3x, β3β3β *b3x, β3x3β *b3β, s3s3s *b3s, s3s3s *b3s (faceting only)

s4x3x3x

demi( . . . . ) | 192 ♦  1  1  1  1 |  1  1  1  1  1  1 | 1  1 1 1
----------------+-----+-------------+-------------------+---------
demi( . x . . ) |   2 | 96  *  *  * |  1  1  1  0  0  0 | 1  1 1 0
demi( . . x . ) |   2 |  * 96  *  * |  0  1  0  1  1  0 | 1  0 1 1
demi( . . . x ) |   2 |  *  * 96  * |  0  0  1  1  0  1 | 0  1 1 1
sefa( s4x . . ) |   2 |  *  *  * 96 |  1  0  0  0  1  1 | 1  1 0 1
----------------+-----+-------------+-------------------+---------
      s4x . .   ♦   4 |  2  0  0  2 | 48  *  *  *  *  * | 1  1 0 0
demi( . x3x . ) |   6 |  3  3  0  0 |  * 32  *  *  *  * | 1  0 1 0
demi( . x . x ) |   4 |  2  0  2  0 |  *  * 48  *  *  * | 0  1 1 0
demi( . . x3x ) |   6 |  0  3  3  0 |  *  *  * 32  *  * | 0  0 1 1
sefa( s4x3x . ) |   6 |  0  3  0  3 |  *  *  *  * 32  * | 1  0 0 1
sefa( s4x . x ) |   4 |  0  0  2  2 |  *  *  *  *  * 48 | 0  1 0 1
----------------+-----+-------------+-------------------+---------
      s4x3x .   ♦  24 | 12 12  0 12 |  6  4  0  0  4  0 | 8  * * *
      s4x . x   ♦   8 |  4  0  4  4 |  2  0  2  0  0  2 | * 24 * *
demi( . x3x3x ) ♦  24 | 12 12 12  0 |  0  4  6  4  0  0 | *  * 8 *
sefa( s4x3x3x ) ♦  24 |  0 12 12 12 |  0  0  0  4  4  6 | *  * * 8

starting figure: x4x3x3x

xuxxxux3xxuxuxx4oooqooo&#xt   → all heights = 1/sqrt(2) = 0.707107
(toe || pseudo (u,x)-toe || pseudo (x,u)-toe || pseudo (x,x,q)-girco || pseudo (x,u)-toe || pseudo (u,x)-toe || toe)

o......3o......4o......      & | 48  *  *  * ♦  1  2  1  0  0  0  0  0  0 |  2  1  1  2  0  0  0  0 0 | 1  2  1 0  0
.o.....3.o.....4.o.....      & |  * 48  *  * ♦  0  0  1  2  1  0  0  0  0 |  0  0  1  2  1  2  0  0 0 | 0  2  1 1  0
..o....3..o....4..o....      & |  *  * 48  * ♦  0  0  0  0  1  1  2  0  0 |  0  0  1  0  0  2  2  1 0 | 0  2  0 1  1
...o...3...o...4...o...        |  *  *  * 48 ♦  0  0  0  0  0  0  2  1  1 |  0  0  0  0  0  2  2  1 1 | 0  2  0 1  1
-------------------------------+-------------+----------------------------+---------------------------+-------------
x...... ....... .......      & |  2  0  0  0 | 24  *  *  *  *  *  *  *  * |  2  0  1  0  0  0  0  0 0 | 1  2  0 0  0
....... x...... .......      & |  2  0  0  0 |  * 48  *  *  *  *  *  *  * |  1  1  0  1  0  0  0  0 0 | 1  1  1 0  0
oo.....3oo.....4oo.....&#x   & |  1  1  0  0 |  *  * 48  *  *  *  *  *  * |  0  0  1  2  0  0  0  0 0 | 0  2  1 0  0
....... .x..... .......      & |  0  2  0  0 |  *  *  * 48  *  *  *  *  * |  0  0  0  1  1  1  0  0 0 | 0  1  1 1  0
.oo....3.oo....4.oo....&#x   & |  0  1  1  0 |  *  *  *  * 48  *  *  *  * |  0  0  1  0  0  2  0  0 0 | 0  2  0 1  0
..x.... ....... .......      & |  0  0  2  0 |  *  *  *  *  * 24  *  *  * |  0  0  1  0  0  0  2  0 0 | 0  2  0 0  1
..oo...3..oo...4..oo...&#x   & |  0  0  1  1 |  *  *  *  *  *  * 96  *  * |  0  0  0  0  0  1  1  1 0 | 0  1  0 1  1
...x... ....... .......        |  0  0  0  2 |  *  *  *  *  *  *  * 24  * |  0  0  0  0  0  0  2  0 1 | 0  2  0 0  1
....... ...x... .......        |  0  0  0  2 |  *  *  *  *  *  *  *  * 24 |  0  0  0  0  0  2  0  0 1 | 0  2  0 1  0
-------------------------------+-------------+----------------------------+---------------------------+-------------
x......3x...... .......      & |  6  0  0  0 |  3  3  0  0  0  0  0  0  0 | 16  *  *  *  *  *  *  * * | 1  1  0 0  0
....... x......4o......      & |  4  0  0  0 |  0  4  0  0  0  0  0  0  0 |  * 12  *  *  *  *  *  * * | 1  0  1 0  0
xux.... ....... .......&#xt  & |  2  2  2  0 |  1  0  2  0  2  1  0  0  0 |  *  * 24  *  *  *  *  * * | 0  2  0 0  0
....... xx..... .......&#x   & |  2  2  0  0 |  0  1  2  1  0  0  0  0  0 |  *  *  * 48  *  *  *  * * | 0  1  1 0  0
....... .x.....4.o.....      & |  0  4  0  0 |  0  0  0  4  0  0  0  0  0 |  *  *  *  * 12  *  *  * * | 0  0  1 1  0
....... .xux... .......&#xt  & |  0  2  2  2 |  0  0  0  1  2  0  2  0  1 |  *  *  *  *  * 48  *  * * | 0  1  0 1  0
..xx... ....... .......&#x   & |  0  0  2  2 |  0  0  0  0  0  1  2  1  0 |  *  *  *  *  *  * 48  * * | 0  1  0 0  1
....... ....... ..oqo..&#xt    |  0  0  2  2 |  0  0  0  0  0  0  4  0  0 |  *  *  *  *  *  *  * 24 * | 0  0  0 1  1
...x...3...x... .......        |  0  0  0  6 |  0  0  0  0  0  0  0  3  3 |  *  *  *  *  *  *  *  * 8 | 0  2  0 0  0
-------------------------------+-------------+----------------------------+---------------------------+-------------
x......3x......4o......      & ♦ 24  0  0  0 | 12 24  0  0  0  0  0  0  0 |  8  6  0  0  0  0  0  0 0 | 2  *  * *  *
xuxx...3xxux... .......&#xt  & ♦  6  6  6  6 |  3  3  6  3  6  3  6  3  3 |  1  0  3  3  0  3  3  0 1 | * 16  * *  *
....... xx.....4oo.....&#x   & ♦  4  4  0  0 |  0  4  4  4  0  0  0  0  0 |  0  1  0  4  1  0  0  0 0 | *  * 12 *  *
....... .xuxux.4.ooqoo.&#xt    ♦  0  8  8  8 |  0  0  0  8  8  0 16  0  4 |  0  0  0  0  2  8  0  4 0 | *  *  * 6  *
..xxx.. ....... ..oqo..&#xt    ♦  0  0  4  4 |  0  0  0  0  0  2  8  2  0 |  0  0  0  0  0  0  4  2 0 | *  *  * * 12

oqQ3ooo3qoo4xux&#zxt   → all existing heights = 0, Q = 2q = 2.828427

o..3o..3o..4o..      | 64  *  * ♦  1   3  0  0 |  3  3  0 |  3 0  1
.o.3.o.3.o.4.o.      |  * 64  * ♦  0   3  1  0 |  3  3  0 |  3 0  1
..o3..o3..o4..o      |  *  * 64 ♦  0   0  1  3 |  0  3  3 |  3 1  0
---------------------+----------+--------------+----------+--------
... ... ... x..      |  2  0  0 | 32   *  *  * |  0  3  0 |  3 0  0
oo.3oo.3oo.4oo.&#x   |  1  1  0 |  * 192  *  * |  2  1  0 |  2 0  1
.oo3.oo3.oo4.oo&#x   |  0  1  1 |  *   * 64  * |  0  3  0 |  3 0  0
... ... ... ..x      |  0  0  2 |  *   *  * 96 |  0  1  2 |  2 1  0
---------------------+----------+--------------+----------+--------
oq. ... qo. ...&#zx  |  2  2  0 |  0   4  0  0 | 96  *  * |  1 0  1
... ... ... xux&#xt  |  2  2  2 |  1   2  2  1 |  * 96  * |  2 0  0
... ... ..o4..x      |  0  0  4 |  0   0  0  4 |  *  * 48 |  1 1  0
---------------------+----------+--------------+----------+--------
oqQ ... qoo4xux&#zxt ♦  8  8  8 |  4  16  8  8 |  4  8  2 | 24 *  *
... ..o3..o4..x      ♦  0  0  8 |  0   0  0 12 |  0  0  6 |  * 8  *
oq.3oo.3qo. ...&#zx  ♦  4  4  0 |  0  12  0  0 |  6  0  0 |  * * 16