----
2D
----
Cases x-n/d-o
Regular polygons (i.e. with winding number d = 1) do exist for n = 3 until n = ∞.
Larger winding numbers d will produce[[:space:]]starry[[:space:]]polygons, sometimes also called polygrams.
The reading here is to have n consecutive sides, arranged with alike dihedral angles,
such that after d circuits around the polygonal center the polygram would close again.
Speaking of polygrams, i.e. using a greek term, it would be best to have a greekish winding term here too. That one then is multistropic.
Hence we distinguish the distrophic heptagram x-7/2-o from the tristrophic heptagram x-7/3-o.
Further the distrophic hexagram x-6/2-o would not mark the Star of David,
but a twice looped hexagon which just looks like a single triangle.
Right by definition the central density of a polygram x-n/d-o happens to be d (as long d < n).
|
Dynkin diagram
|
x-n/d-o
|
|
Schläfli symbol
|
{n/d}
|
|
Circumradius
|
1/(2 sin(π d/n))
|
|
Inradius
|
1/(2 tan(π d/n))
|
|
|
Circ. : Inrad. = 1 : cos(π d/n) = 2 : x(n/d)
|
|
Vertex angle
|
π (1 - 2d/n)
|
|
Chord lengths
|
x(n/d,m) = sin(π md/n) / sin(π d/n)
|
|
|
x(n/d) = x(n/d,2) = 2 cos(π d/n)
|
|
Area *)
|
n/(4 tan(π d/n))
|
|
|
Area : (Circ.2) = sin(2π d/n) : 2/n
|
*) Area formula (for unit edges) here is density weighted, i.e. subregions with multiple density (as occuring in polygrams) will be counted multiply in accordance.
It is derived from the 2n right triangles, each outlined by center of polygon, center of side, and vertex:
An = 2n·(1/2)·rn cos(π d/n)·rn sin(π d/n),
then inserting the above formula for the circumradius rn.
On the other hand, by means of that area formula, one derives An/(rn2) = sin(2π d/n) n/2,
where the first factor might be reconsidered to be nothing but the heights of the neighbouring vertices above the line-span of a polygon's side.
The upper limit of the winding number clearly is given by d < n.
But any number d > n/2 produces a retrograde circuit which looks not different to the corresponding prograde one with d' = n - d, only that its circuit would be reversed.
For true polygrams (i.e. d > 1) be aware of the cases where n and d do have a common divisor, say k.
In those cases the resulting polygram looks like the polygram with n/k edges (this is now integral), wound up d/k times (again integral).
But in fact both, the edges and vertices do coincide k times.

x-3-o
|

x-4-o
|
x-5-o
|

x-5/2-o
(central region is of density 2)
|
trig (alt: equit)
(equilateral) triangle, pyrogon
|
square
square, geogon
|
peg
pentagon, cosmogon
|
star
pentagram
|
Circ. =
1/sqrt(3) = 0.577350
|
Circ. =
1/sqrt(2) = 0.707107
|
Circ. =
sqrt[(5+sqrt(5))/10] = 0.850651
|
Circ. =
sqrt[(5-sqrt(5))/10] = 0.525731
|
Inrad. =
1/sqrt(12) = 0.288675
|
Inrad. =
1/2
|
Inrad. =
sqrt[(5+2 sqrt(5))/20] = 0.688191
|
Inrad. =
sqrt[(5-2 sqrt(5))/20] = 0.162460
|
|
Circ. : Inrad. = 2 : x
|
Circ. : Inrad. = 2 : q
|
Circ. : Inrad. = 2 : f
|
Circ. : Inrad. = 2 : v
|
Height =
sqrt(3)/2 = 0.866025
|
Height =
1
|
Height =
sqrt[5+2 sqrt(5)]/2 = 1.538842
|
Height =
sqrt[(5+sqrt(5))/8] = 0.951057
|
Height(1,2) =
sqrt[(5-sqrt(5))/8] = 0.587785
|
Height(1,2) =
sqrt[5-2 sqrt(5)]/2 = 0.363271
|
Height(2,3) =
sqrt[(5+sqrt(5))/8] = 0.951057
|
Height(2,3) =
sqrt[(5-sqrt(5))/8] = 0.587785
|
|
H.(1,2) : H.(2,3) = 1 : f
|
H.(1,2) : H.(2,3) = 1 : f
|
|
x(3,1) = x = 1
|
x(4,1) = x = 1
x(4,2) = q = sqrt(2) = 1.414214
|
x(5,1) = x = 1
x(5,2) = f = (1+sqrt(5))/2 = 1.618034
|
x(5/2,1) = x = 1
x(5/2,2) = v = (sqrt(5)-1)/2 = 0.618034
|
|
Vertex angle = 60°
|
Vertex angle = 90°
|
Vertex angle = 108°
|
Vertex angle = 36°
|
Area =
sqrt(3)/4 = 0.433013
|
Area = 1
|
Area =
sqrt[25+10 sqrt(5)]/4 = 1.720477
|
Area (weighted) =
sqrt[25-10 sqrt(5)]/4 = 0.406150
|
Area : (Circ.2) =
3 Height/2 = 1.299038
|
Area : (Circ.2) = 2
|
Area : (Circ.2) =
5 Height(2,3)/2 = 2.377641
|
Area : (Circ.2) =
5 Height(2,3)/2 = 1.469463
|
Incidence matrix according to Dynkin symbol
x-n/d-o
. . | n | 2
--------+---+--
x . | 2 | n
Cases x-n/d-x
There is a general operator applicable to all polygons or polygrams called truncation.
The truncated polygram
trunc( x-n/d-o ) = x-n/d-y
has 2n sides, half of which are maintained from before (marked x above), half of which are derived from truncation of the vertices (marked y above).
Here x and y denote sides of different length in general.
Those 2n sides still cycle around the center d times.
For the regular representation the lengths obviously are the same (i.e. |y| = |x|, thus assumed to be unity).
Therefore there is the equivalence
x-n/d-x = x-2n/d-o
which even supports the global orientation.
(The more general case of different lengths is considered later.)
|
Dynkin diagram
|
x-n/d-x
|
|
Circumradius
|
1/(2 sin(π d/2n))
|
|
Inradius
|
1/(2 tan(π d/2n))
|
|
Vertex angle
|
π (1 - d/n)
|
|
Chord lengths
|
x(2n/d,m) = | sin(π md/2n)/sin(π d/2n) |
|
x-3-x
|
x-4-x
|

x-4/3-x
(central region is of density 3,
triangles are of density 2)
|
x-5-x
|
hig
hexagon
|
oc
octagon
|
og
octagram
|
dec
decagon
|
Circ. =
1
|
Circ. =
sqrt[(2+sqrt(2))/2] = 1.306563
|
Circ. =
sqrt[(2-sqrt(2))/2] = 0.541196
|
Circ. =
(1+sqrt(5))/2 = 1.618034
|
Inrad. =
sqrt(3)/2 = 0.866025
|
Inrad. =
(1+sqrt(2))/2 = 1.207107
|
Inrad. =
(sqrt(2)-1)/2 = 0.207107
|
Inrad. =
sqrt[5+2 sqrt(5)]/2 = 1.538842
|
|
Circ. : Inrad. = 2 : h
|
Circ. : Inrad. = 2 : k
|
Circ. : Inrad. = 2 : x(8/3)
|
Circ. : Inrad. = 2 : x(10)
|
x(6,1) = x = 1
x(6,2) = h = sqrt(3) = 1.732051
x(6,3) = u = 2
|
x(8,1) = x = 1
x(8,2) = k = sqrt[2+sqrt(2)] = 1.847759
x(8,3) = w = 1+sqrt(2) = 2.414214
x(8,4) = sqrt(4+2 sqrt(2)) = 2.613126
|
x(8/3,1) = x = 1
x(8/3,2) = sqrt[2-sqrt(2)] = 0.765367
x(8/3,3) = sqrt(2)-1 = 0.414214
x(8/3,4) = sqrt(4-2 sqrt(2)) = 1.082392
|
x(10,1) = x = 1
x(10,2) = sqrt[(5+sqrt(5))/2] = 1.902113
x(10,3) = f f = (3+sqrt(5))/2 = 2.618034
x(10,4) = sqrt[5+2 sqrt(5)] = 3.077684
x(10,5) = u f = 1+sqrt(5) = 3.236068
|
|
Vertex angle = 120°
|
Vertex angle = 135°
|
Vertex angle = 45°
|
Vertex angle = 144°
|
Area =
3 sqrt(3)/2 = 2.598076
|
Area =
2[1+sqrt(2)] = 4.828427
|
Area (weighted) =
2[sqrt(2)-1] = 0.828427
|
Area =
5 sqrt[5+2 sqrt(5)]/2 = 7.694209
|
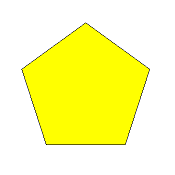
x-5/2-x
doubly wound decagon
|

x-5/3-x
(central region is of density 3,
triangles are of density 2)
|

x-6-x
|

x-6/5-x
(central region is of density 5,
triangles are of density 4,
kites are of densities 3, 2, and 1)
|
–
|
deg
decagram
|
twig (alt.: dog)
dodecagon
|
stwig (alt.: dodag)
dodecagram
|
Circ. =
sqrt[(5+sqrt(5))/10] = 0.850651
|
Circ. =
(sqrt(5)-1)/2 = 0.618034
|
Circ. =
(1+sqrt(3))/sqrt(2) = 1.931852
|
Circ. =
(sqrt(3)-1)/sqrt(2) = 0.517638
|
Inrad. =
sqrt[(5+2 sqrt(5))/20] = 0.688191
|
Inrad. =
sqrt[5-2 sqrt(5)]/2 = 0.363271
|
Inrad. =
(2+sqrt(3))/2 = 1.866025
|
Inrad. =
(2-sqrt(3))/2 = 0.133975
|
|
Circ. : Inrad. = 2 : f
|
Circ. : Inrad. = 2 : x(10/3)
|
Circ. : Inrad. = 2 : x(12)
|
Circ. : Inrad. = 2 : x(12/5)
|
x(10/2,1) = x = 1
x(10/2,2) = f = (1+sqrt(5))/2 = 1.618034
x(10/2,3) = f = (1+sqrt(5))/2 = 1.618034
x(10/2,4) = x = 1
x(10/2,5) = 0
|
x(10/3,1) = x = 1
x(10/3,2) = sqrt[(5-sqrt(5))/2] = 1.175571
x(10/3,3) = v v = (3-sqrt(5))/2 = 0.381966
x(10/3,4) = sqrt[5-2 sqrt(5)] = 0.726543
x(10/3,5) = u v = sqrt(5)-1 = 1.236068
|
x(12,1) = x = 1
x(12,2) = sqrt[2+sqrt(3)] = 1.931852
x(12,3) = x+h = 1+sqrt(3) = 2.732051
x(12,4) = sqrt[3(2+sqrt(3))] = 3.346065
x(12,5) = u+h = 2+sqrt(3) = 3.732051
|
x(12/5,1) = x = 1
x(12/5,2) = sqrt[2-sqrt(3)] = 0.517638
x(12/5,3) = h-x = sqrt(3)-1 = 0.732051
x(12/5,4) = sqrt[3(2-sqrt(3))] = 0.896575
x(12/5,5) = u-h = 2-sqrt(3) = 0.267949
|
|
Vertex angle = 108°
|
Vertex angle = 72°
|
Vertex angle = 150°
|
Vertex angle = 30°
|
Area (weighted) =
sqrt[25+10 sqrt(5)]/2 = 3.440955
|
Area (weighted) =
5 sqrt[5-2 sqrt(5)]/2 = 1.816356
|
Area =
3(2+sqrt(3)) = 11.196152
|
Area (weighted) =
3(2-sqrt(3)) = 0.803848
|
Incidence matrix according to Dynkin symbol
x-n/d-x
. . | 2n | 1 1
--------+----+----
x . | 2 | n *
. x | 2 | * n
Cases x-n/d-y
Semiregular polygons do exist in 2 different kinds. Either sides would be alike, but angles would alternate (f.i. a rhomb),
or the other way round, angles are alike, but side-lengths do alternate (f.i. a rectangle).
Here the second of these dual types will be considered.
Obviously that one occures as the general member in the truncational process of the x-n/d-o polygon.
- In contrast to the other chapters, x here would mark a side of arbitrary length |x|
and y being one of independent arbitrary length |y|.
The special case, where |x| = |y| = 1 leads us back to the former case of x-n/d-x.
|
Dynkin diagram
|
x-n/d-y
|
|
Circumradius
|
sqrt[|x|2 + |y|2 + 2 |x| |y| cos(π d/n)]/(2 sin(π d/n))
|
|
Inradius to x-side
|
|y|/(2 sin(π d/n)) + |x|/(2 tan(π d/n)) = [|y| + |x| cos(π d/n)]/(2 sin(π d/n))
|
|
Inradius to y-side
|
|x|/(2 sin(π d/n)) + |y|/(2 tan(π d/n)) = [|x| + |y| cos(π d/n)]/(2 sin(π d/n))
|
|
Vertex angle
|
π (1 - d/n)
|
E.g. for the semiregular hexagon the circumradius evaluates to sqrt[(|x|2 + |x| |y| + |y|2)/3].
|
x y
|
semiregular tetragon
|
rectangle
|
rect
|
|
x3y
|
semiregular hexagon
|
ditrigon
|
dit
|
|
x4y
|
semiregular octagon
|
ditetragon
|
diteg
|
|
x5y
|
semiregular decagon
|
dipentagon
|
dipeg
|
|
x6y
|
semiregular dodecagon
|
dihexagon
|
dihig
|
Further readings: analoguous outline of different cases, but dimensionally independant generalization.
Cases s-n/d-o resp. β-n/d-o and s-n/d-s
A further general operation commonly is called snubbing.
Here snubbing in fact is understood as an alternated faceting.
For even n a snub can be obtained if only every second vertex is used, while the ones between are omitted.
For truncates it applies to any n. Snubbing reduces the vertex count to the half.
|
Dynkin diagram
|
s-n/d-o
|
|
Vertex angle
|
π (1 - (4d/n mod 2))
|
|
Dynkin diagram
|
s-n/d-s
|
|
Vertex angle
|
π (1 - 2d/n)
|
Right from the angles one can rewrite those snubs as truncations according to
s-n/d-o = y-m/(d mod m)-o (where n = 2m)
s-n/d-s = y-n/d-o
where the side lengths y are to be chosen such that the latter polygons are vertex inscribed to the arguments of the former ones.
For odd n an analogue process can be applied to untruncated polygons too if the alternated faceting would be understood locally only.
This is what is called a holosnub.
In order to close back again, in contrary to mere snubs, the process has to cycle around twice.
So in total all vertices will have to be used, both to be retained in one circuit and to be omitted in the other.
Thus the vertex count will stay the same as that of the starting figure.
|
Dynkin diagram
|
β-n/d-o
|
|
Vertex angle
|
π (1 - (4d/n mod 2))
|
|
Size ratio
|
x : x(n/d) = x(n/d,1) : x(n/d,2) = sin(π d/n) : sin(π 2d/n) = 1 : 2 cos(π d/n)
|
Again one can rewrite those holosnubs right from the angles as truncations according to
β-n/d-o = y-n/(2d mod n)-o
where side lengths y are as above.
Clearly can holosnubbing be applied to even n too, but then the described result would again omit half the vertices of the argument figure, while the remaining ones are used twice, i.e. n/(2d mod n) will be reducible even if n/d was irreducible.

β-3-o
retrograde triangle
x:x = 1:1
|
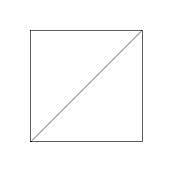
s-4-o
x:q = 1:sqrt(2) = 1:1.414214
|
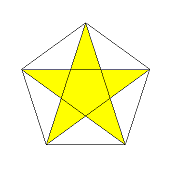
β-5-o
(central region is of density 2)
x:f = 2:(1+sqrt(5)) = 1:1.618034
|
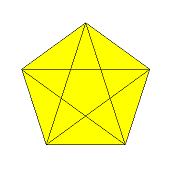
β-5/2-o
retrograde pentagon
(density 1 throughout)
x:v = 2:(sqrt(5)-1) = 1:0.618034
|
s-3-s
x:h = 1:sqrt(3) = 1:1.732051
|
s-4-s
x:k = 1:sqrt[2+sqrt(2)]
= 1:1.847759
|
s-5-s
x:x(10) = 1:sqrt[(5+sqrt(5))/2]
= 1:1.902113
|
s-5/2-s
(central region is of density 2)
x:f = 2:(1+sqrt(5)) = 1:1.618034
|
Incidence matrix according to Dynkin symbol
s-n/d-o (n=2m)
demi( . . ) | m | 2
----------------+---+--
sefa( s-n/d-o ) | 2 | m
β-n/d-o (n odd)
both( . . ) | n | 2
----------------+---+--
sefa( β-n/d-o ) | 2 | n
s-n/d-s
demi( . . ) | n | 2
----------------+---+--
sefa( s-n/d-s ) | 2 | n
Cases s-n/d-x resp. β-n/d-x
But snubbing does not restrict itself to alternation of vertices.
Alike, edges could be alternated.
And this is especially interesting for the truncated polygons or truncated polygrams.
That is, take one half of the sides, say those which correspond to the first x of the diagram,
and from that group use only every second one, while the ones in between will be replaced by the chords underneath;
the other group of sides will be ignored completely.
|
Dynkin diagram
|
s-n/d-x , β-n/d-x
|
|
Vertex angle
|
π (1 - 2d/n) if 3d < 2n
2π (1 - d/n) if 3d > 2n
|
|
Size ratio
|
x : y = x : x(n/d,3) = sin(π d/n) : sin(π 3d/n) = 1 : ([2 cos(π d/n)]2-1) = 1 : ([x(n/d)]2-1)
|
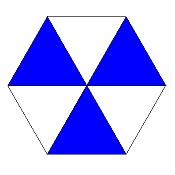
β-3-x
x:u = 1:2
regular version = x-6/2-o
(then density 2 all over)
|
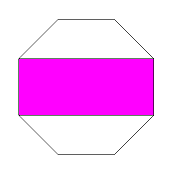
s-4-x
x:w = 1:(1+sqrt(2))
= 1:2.414214
regular version = x-4-o
|
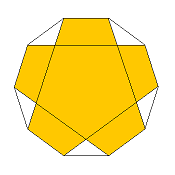
β-5-x
(central region is of density 2)
x:F = 2:(3+sqrt(5))
= 1:2.618034
regular version = x-10/2-o
(then density 2 all over)
|
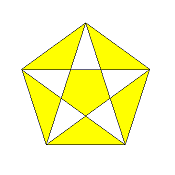
β-5/2-x
(center of density -1)
x:f = 2:(1+sqrt(5)) = 1:1.618034
regular version = x-10/4-o
(then arms of density 2,
center of density 4)
|
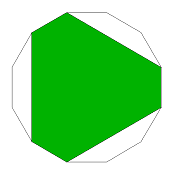
s-6-x
x:e = 1:(1+sqrt(3)) = 1:2.732051
regular version = x-6-o
|
Right from the angles one can rewrite those snubs or holosnubs as truncations according to
s-n/d-x = x-m/d-y (3d < 2n; n even)
= x-m/(d - m)-y (3d > 2n; n even, m = n/2)
β-n/d-x = x-n/2d-y (3d < 2n; n odd)
= x-n/(2d - n)-y (3d > 2n; n odd)
where x and y denote sides of different length in general.
For the continuous change of the side lengths ratio to |y|/|x| → 1 one comes back to regular representations obviously.
s-n/d-x → x-n/d-o (3d < 2n; n even)
→ x-n/(d - m)-o (3d > 2n; n even, m = n/2)
β-n/d-x → x-2n/2d-o (3d < 2n; n odd)
→ x-2n/(2d - n)-o (3d > 2n; n odd)
Usually the latter transition is subsumed to be done too.
Incidence matrix according to Dynkin symbol
s-n/d-x (n=2m; 3d <> 2n)
demi( . . ) | 2m | 1 1
----------------+----+----
demi( . x ) | 2 | m *
sefa( s-n/d-x ) | 2 | * m
β-n/d-x (n odd; 3d <> 2n)
both( . . ) | 2n | 1 1
----------------+----+----
both( . x ) | 2 | n *
sefa( β-n/d-x ) | 2 | * n
Note that the former transition |y|/|x| → 1 would not be possible for 3d = 2n,
as in the mere alternated faceting of a regular figure one has |y| = 0.
Those edges sefa( s-n/d-x ) respectively sefa( β-n/d-x ) having zero length therefore should be omitted.
By the resulting vertex identification the vertex count will be halved as well.
|
Dynkin diagram
|
s-n/d-x , β-n/d-x (where 3d = 2n)
|
|
Vertex angle
|
π/3
|
s-n/d-x (n=2m; 3d = 2n)
quart( . . ) | m | 2
-----------------+---+--
demi( . x ) | 2 | m
β-n/d-x (n odd; 3d = 2n)
demi( . . ) | n | 2
----------------+---+---
both( . x ) | 2 | n
























