tah

Acronym tah

Name tesseractihexadecachoron,
bitruncated tesseract,
bitruncated hexadecachoron,
runcicantic tesseract

©

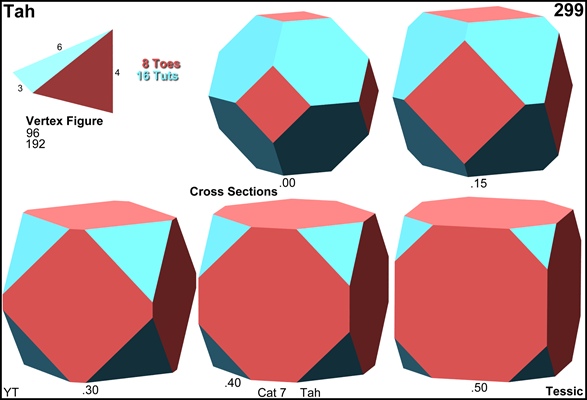
Cross sections

©

Circumradius sqrt(9/2) = 2.121320

Inradius
wrt. toe sqrt(2) = 1.414214

Inradius
wrt. tut 5/sqrt(8) = 1.767767

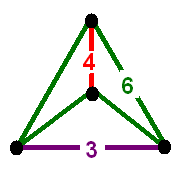
Vertex figure

©

Vertex layers

Layer	Symmetry	Subsymmetries
	`o3o3o4o`	`o3o3o .`	`o3o . o`	`o . o4o`	`. o3o4o`
1	`o3x3x4o`	`o3x3x .` tut first	`o3x . o` {3} first	`o . x4o` {4} first	`. x3x4o` toe first
2		`o3u3x .`	`o3u . q`	`x . u4o`	`. o3u4o`
3a		`x3x3u .`	`x3x . Q`	`u . x4q`	`. o3x4q`
3b		`x3x3u .`	`o3H . o`	`u . x4q`	`. o3x4q`
4a		`u3x3x .`	`u3x . Q`	`H . u4o`	`. o3u4o`
4b		`u3x3x .`	`x3H . o`	`x . o4Q`	`. o3u4o`
5		`x3u3o .`	`u3u . Q`	`U . x4o`	`. x3x4o` opposite toe
6a		`x3x3o .` opposite tut	`x3u . Q`	`H . u4o`
6b		`x3x3o .` opposite tut	`H3x . o`	`x . o4Q`
7a			`x3x . Q`	`u . x4q`
7b			`H3o . o`	`u . x4q`
8			`u3o . q`	`x . u4o`
9			`x3o . o` opposite {3}	`o . x4o` opposite {4}
	`o3o3o *b3o`	`o3o3o .`	`o3o . *b3o`	`o . o o`	`. o3o *b3o`
1	`x3x3x *b3o`	`x3x3x .` toe first	`x3x . *b3o` tut first	`x . x o` {4} first	`. x3x *b3o` tut first
2		`u3o3u .`	`x3u . *b3o`	`u . u x`	`. u3x *b3o`
3a		`H3o3x .`	`u3x . *b3x`	`H . x u`	`. x3u *b3x`
3b		`x3o3H .`	`u3x . *b3x`	`x . H u`	`. x3u *b3x`
4a		`u3o3u .`	`x3x . *b3u`	`u . u H`	`. x3x *b3u`
4b				`U . o x`
4c				`o . U x`
5		`x3x3x .` opposite toe	`o3u . *b3x`	`x . x U`	`. u3o *b3x`
6a			`o3x . *b3x` opposite tut	`u . u H`	`. x3o *b3x` opposite tut
6b				`U . o x`
6c				`o . U x`
7a				`H . x u`
7b				`x . H u`
8				`u . u x`
9				`x . x o` opposite {4}

(Q=2q, H=3x, U=4x)

Lace city
in approx. ASCII-art

©	x4o u4o x4q u4o x4o -- x3x4o (toe) u4o o4Q u4o -- o3u4o (u-co) x4q o4Q o4Q x4q -- o3x4q ((q,x)-tic) u4o o4Q u4o -- o3u4o (u-co) x4o u4o x4q u4o x4o -- x3x4o (toe)

                       		_+-- x3x3o (tut)
                       
                       		_+-- x3u3o ((x,u)-tut)
                       
          x3o          		_+-- u3x3x ((u,x,x)-toe)
     u3o       u3o     
x3x       H3o       x3x		_+-- x3x3u (inv. (u,x,x)-toe)
                       
x3u       H3x       x3u		_+-- o3u3x (inv. (x,u)-tut)
     u3u       u3u     
u3x       x3H       u3x		_+-- o3x3x (inv. tut)
                       
x3x       o3H       x3x
     o3u       o3u     
          o3x          

 |    |    |    |    |
 |    |    |    |    +-- x3x4o (toe)
 |    |    |    +------- o3u4o (u-co)
 |    |    +------------ o3x4q ((q,x)-tic)
 |    +----------------- o3u4o (u-co)
 +---------------------- x3x4o (toe)

Coordinates

(sqrt(2), sqrt(2), 1/sqrt(2), 0) & all permutations, all changes of sign
: tah in tessic orientation
(5/sqrt(8), 3/sqrt(8), 1/sqrt(8), 1/sqrt(8)) & all permutations, all even changes of sign
: tah in demitessic orientation

Volume 307/6 = 51.166667

General of army (is itself convex)

Colonel of regiment

(is itself locally convex – uniform polychoral members:

by cells:	toe	tut
tah	8	16

)

Dihedral angles

at {6} between toe and tut: 120°
at {3} between tut and tut: 120°
at {4} between toe and toe: 90°

Face vector 96, 192, 120, 24

Confer

Grünbaumian relatives:: 2tah
decompositions:: rit || tah
ambification:: retah
general polytopal classes:: Wythoffian polychora lace simplices partial Stott expansions
analogs:: bitruncated hypercube btC_n

External
links

Note that tah can be thought of as the external blend of 1 rit + 16 tetatuts + 8 coatoes. This decomposition is described as the degenerate segmentoteron oo3ox3xx4oo&#x. – Alternatively, although subdimensioanlly degenerate, tah can be decomposed into 1 thex + 16 tutas + 24 squascs + 8 octatoes according to xo3xx3ox4oo&#x.

Incidence matrix according to Dynkin symbol

o3x3x4o

. . . . | 96 |  2  2 |  1  4  1 |  2 2
--------+----+-------+----------+-----
. x . . |  2 | 96  * |  1  2  0 |  2 1
. . x . |  2 |  * 96 |  0  2  1 |  1 2
--------+----+-------+----------+-----
o3x . . |  3 |  3  0 | 32  *  * |  2 0
. x3x . |  6 |  3  3 |  * 64  * |  1 1
. . x4o |  4 |  0  4 |  *  * 24 |  0 2
--------+----+-------+----------+-----
o3x3x . ♦ 12 | 12  6 |  4  4  0 | 16 *
. x3x4o ♦ 24 | 12 24 |  0  8  6 |  * 8

snubbed forms: o3β3x4o, o3x3β4o, o3β3β4o

o3x3x4/3o

. . .   . | 96 |  2  2 |  1  4  1 |  2 2
----------+----+-------+----------+-----
. x .   . |  2 | 96  * |  1  2  0 |  2 1
. . x   . |  2 |  * 96 |  0  2  1 |  1 2
----------+----+-------+----------+-----
o3x .   . |  3 |  3  0 | 32  *  * |  2 0
. x3x   . |  6 |  3  3 |  * 64  * |  1 1
. . x4/3o |  4 |  0  4 |  *  * 24 |  0 2
----------+----+-------+----------+-----
o3x3x   . ♦ 12 | 12  6 |  4  4  0 | 16 *
. x3x4/3o ♦ 24 | 12 24 |  0  8  6 |  * 8

o3/2x3x4o

.   . . . | 96 |  2  2 |  1  4  1 |  2 2
----------+----+-------+----------+-----
.   x . . |  2 | 96  * |  1  2  0 |  2 1
.   . x . |  2 |  * 96 |  0  2  1 |  1 2
----------+----+-------+----------+-----
o3/2x . . |  3 |  3  0 | 32  *  * |  2 0
.   x3x . |  6 |  3  3 |  * 64  * |  1 1
.   . x4o |  4 |  0  4 |  *  * 24 |  0 2
----------+----+-------+----------+-----
o3/2x3x . ♦ 12 | 12  6 |  4  4  0 | 16 *
.   x3x4o ♦ 24 | 12 24 |  0  8  6 |  * 8

o3/2x3x4/3o

.   . .   . | 96 |  2  2 |  1  4  1 |  2 2
------------+----+-------+----------+-----
.   x .   . |  2 | 96  * |  1  2  0 |  2 1
.   . x   . |  2 |  * 96 |  0  2  1 |  1 2
------------+----+-------+----------+-----
o3/2x .   . |  3 |  3  0 | 32  *  * |  2 0
.   x3x   . |  6 |  3  3 |  * 64  * |  1 1
.   . x4/3o |  4 |  0  4 |  *  * 24 |  0 2
------------+----+-------+----------+-----
o3/2x3x   . ♦ 12 | 12  6 |  4  4  0 | 16 *
.   x3x4/3o ♦ 24 | 12 24 |  0  8  6 |  * 8

x3x3x *b3o

. . .    . | 96 |  1  2  1 |  2  1  2  1 | 2 1 1
-----------+----+----------+-------------+------
x . .    . |  2 | 48  *  * |  2  1  0  0 | 2 1 0
. x .    . |  2 |  * 96  * |  1  0  1  1 | 1 1 1
. . x    . |  2 |  *  * 48 |  0  1  2  0 | 2 0 1
-----------+----+----------+-------------+------
x3x .    . |  6 |  3  3  0 | 32  *  *  * | 1 1 0
x . x    . |  4 |  2  0  2 |  * 24  *  * | 2 0 0
. x3x    . |  6 |  0  3  3 |  *  * 32  * | 1 0 1
. x . *b3o |  3 |  0  3  0 |  *  *  * 32 | 0 1 1
-----------+----+----------+-------------+------
x3x3x    . ♦ 24 | 12 12 12 |  4  6  4  0 | 8 * *
x3x . *b3o ♦ 12 |  6 12  0 |  4  0  0  4 | * 8 *
. x3x *b3o ♦ 12 |  0 12  6 |  0  0  4  4 | * * 8

snubbed forms: β3x3x *b3o, x3β3x *b3o, β3β3x *b3o, β3x3β *b3o, β3β3β *b3o

x3x3x *b3/2o

. . .      . | 96 |  1  2  1 |  2  1  2  1 | 2 1 1
-------------+----+----------+-------------+------
x . .      . |  2 | 48  *  * |  2  1  0  0 | 2 1 0
. x .      . |  2 |  * 96  * |  1  0  1  1 | 1 1 1
. . x      . |  2 |  *  * 48 |  0  1  2  0 | 2 0 1
-------------+----+----------+-------------+------
x3x .      . |  6 |  3  3  0 | 32  *  *  * | 1 1 0
x . x      . |  4 |  2  0  2 |  * 24  *  * | 2 0 0
. x3x      . |  6 |  0  3  3 |  *  * 32  * | 1 0 1
. x . *b3/2o |  3 |  0  3  0 |  *  *  * 32 | 0 1 1
-------------+----+----------+-------------+------
x3x3x      . ♦ 24 | 12 12 12 |  4  6  4  0 | 8 * *
x3x . *b3/2o ♦ 12 |  6 12  0 |  4  0  0  4 | * 8 *
. x3x *b3/2o ♦ 12 |  0 12  6 |  0  0  4  4 | * * 8

s4x3x3o

demi( . . . . ) | 96 |  1  2  1 |  1  2  1  2 | 2 1 1
----------------+----+----------+-------------+------
demi( . x . . ) |  2 | 48  *  * |  1  2  0  0 | 2 1 0
demi( . . x . ) |  2 |  * 96  * |  0  1  1  1 | 1 1 1
sefa( s4x . . ) |  2 |  *  * 48 |  1  0  0  2 | 2 0 1
----------------+----+----------+-------------+------
      s4x . .   ♦  4 |  2  0  2 | 24  *  *  * | 2 0 0
demi( . x3x . ) |  6 |  3  3  0 |  * 32  *  * | 1 1 0
demi( . . x3o ) |  3 |  0  3  0 |  *  * 32  * | 0 1 1
sefa( s4x3x . ) |  6 |  0  3  3 |  *  *  * 32 | 1 0 1
----------------+----+----------+-------------+------
      s4x3x .   ♦ 24 | 12 12 12 |  6  4  0  4 | 8 * *
demi( . x3x3o ) ♦ 12 |  6 12  0 |  0  4  4  0 | * 8 *
sefa( s4x3x3o ) ♦ 12 |  0 12  6 |  0  0  4  4 | * * 8

starting figure: x4x3x3o

s4o3x3x

demi( . . . . ) | 96 |  1  2  1 |  1  1  2  2 | 1 1 2
----------------+----+----------+-------------+------
      s4o . .   ♦  2 | 48  *  * |  1  0  0  2 | 1 0 2
demi( . . x . ) |  2 |  * 96  * |  0  1  1  1 | 1 1 1
demi( . . . x ) |  2 |  *  * 48 |  1  0  2  0 | 0 1 2
----------------+----+----------+-------------+------
      s4o . x   |  4 |  2  0  2 | 24  *  *  * | 0 0 2
demi( . o3x . ) |  3 |  0  3  0 |  * 32  *  * | 1 1 0
demi( . . x3x ) |  6 |  0  3  3 |  *  * 32  * | 0 1 1
sefa( s4o3x . ) |  6 |  3  3  0 |  *  *  * 32 | 1 0 1
----------------+----+----------+-------------+------
      s4o3x .   ♦ 12 |  6 12  0 |  0  4  0  4 | 8 * *
demi( . o3x3x ) ♦ 12 |  0 12  6 |  0  4  4  0 | * 8 *
sefa( s4o3x3x ) ♦ 24 | 12 12 12 |  6  0  4  4 | * * 8

starting figure: x4o3x3x

xooox3xuxux4ooqoo&#xt   → all heights = 1/sqrt(2) = 0.707107
(toe || pseudo u-co || pseudo (q,x)-tic || pseudo u-co || toe)

o....3o....4o....     | 24  *  *  *  * |  1  2  1  0  0  0  0  0  0 | 2 1  1  2  0 0  0  0 0 0 | 1 2 1 0 0
.o...3.o...4.o...     |  * 12  *  *  * |  0  0  2  2  0  0  0  0  0 | 0 0  1  4  1 0  0  0 0 0 | 0 2 2 0 0
..o..3..o..4..o..     |  *  * 24  *  * |  0  0  0  1  2  1  0  0  0 | 0 0  0  2  1 1  2  0 0 0 | 0 1 2 1 0
...o.3...o.4...o.     |  *  *  * 12  * |  0  0  0  0  0  2  2  0  0 | 0 0  0  0  1 0  4  1 0 0 | 0 0 2 2 0
....o3....o4....o     |  *  *  *  * 24 |  0  0  0  0  0  0  1  1  2 | 0 0  0  0  0 0  2  1 2 1 | 0 0 1 2 1
----------------------+----------------+----------------------------+--------------------------+----------
x.... ..... .....     |  2  0  0  0  0 | 12  *  *  *  *  *  *  *  * | 2 0  1  0  0 0  0  0 0 0 | 1 2 0 0 0
..... x.... .....     |  2  0  0  0  0 |  * 24  *  *  *  *  *  *  * | 1 1  0  1  0 0  0  0 0 0 | 1 1 1 0 0
oo...3oo...4oo...&#x  |  1  1  0  0  0 |  *  * 24  *  *  *  *  *  * | 0 0  1  2  0 0  0  0 0 0 | 0 2 1 0 0
.oo..3.oo..4.oo..&#x  |  0  1  1  0  0 |  *  *  * 24  *  *  *  *  * | 0 0  0  2  1 0  0  0 0 0 | 0 1 2 0 0
..... ..x.. .....     |  0  0  2  0  0 |  *  *  *  * 24  *  *  *  * | 0 0  0  1  0 1  1  0 0 0 | 0 1 1 1 0
..oo.3..oo.4..oo.&#x  |  0  0  1  1  0 |  *  *  *  *  * 24  *  *  * | 0 0  0  0  1 0  2  0 0 0 | 0 0 2 1 0
...oo3...oo4...oo&#x  |  0  0  0  1  1 |  *  *  *  *  *  * 24  *  * | 0 0  0  0  0 0  2  1 0 0 | 0 0 1 2 0
....x ..... .....     |  0  0  0  0  2 |  *  *  *  *  *  *  * 12  * | 0 0  0  0  0 0  0  1 2 0 | 0 0 0 2 1
..... ....x .....     |  0  0  0  0  2 |  *  *  *  *  *  *  *  * 24 | 0 0  0  0  0 0  1  0 1 1 | 0 0 1 1 1
----------------------+----------------+----------------------------+--------------------------+----------
x....3x.... .....     |  6  0  0  0  0 |  3  3  0  0  0  0  0  0  0 | 8 *  *  *  * *  *  * * * | 1 1 0 0 0
..... x....4o....     |  4  0  0  0  0 |  0  4  0  0  0  0  0  0  0 | * 6  *  *  * *  *  * * * | 1 0 1 0 0
xo... ..... .....&#x  |  2  1  0  0  0 |  1  0  2  0  0  0  0  0  0 | * * 12  *  * *  *  * * * | 0 2 0 0 0
..... xux.. .....&#xt |  2  2  2  0  0 |  0  1  2  2  1  0  0  0  0 | * *  * 24  * *  *  * * * | 0 1 1 0 0
..... ..... .oqo.&#xt |  0  1  2  1  0 |  0  0  0  2  0  2  0  0  0 | * *  *  * 12 *  *  * * * | 0 0 2 0 0
..o..3..x.. .....     |  0  0  3  0  0 |  0  0  0  0  3  0  0  0  0 | * *  *  *  * 8  *  * * * | 0 1 0 1 0
..... ..xux .....&#xt |  0  0  2  2  2 |  0  0  0  0  1  2  2  0  1 | * *  *  *  * * 24  * * * | 0 0 1 1 0
...ox ..... .....&#x  |  0  0  0  1  2 |  0  0  0  0  0  0  2  1  0 | * *  *  *  * *  * 12 * * | 0 0 0 2 0
....x3....x .....     |  0  0  0  0  6 |  0  0  0  0  0  0  0  3  3 | * *  *  *  * *  *  * 8 * | 0 0 0 1 1
..... ....x4....o     |  0  0  0  0  4 |  0  0  0  0  0  0  0  0  4 | * *  *  *  * *  *  * * 6 | 0 0 1 0 1
----------------------+----------------+----------------------------+--------------------------+----------
x....3x....4o....     ♦ 24  0  0  0  0 | 12 24  0  0  0  0  0  0  0 | 8 6  0  0  0 0  0  0 0 0 | 1 * * * *
xoo..3xux.. .....&#xt ♦  6  3  3  0  0 |  3  3  6  3  3  0  0  0  0 | 1 0  3  3  0 1  0  0 0 0 | * 8 * * *
..... xuxux4ooqoo&#xt ♦  4  4  8  4  4 |  0  4  4  8  4  8  4  0  4 | 0 1  0  4  4 0  4  0 0 1 | * * 6 * *
..oox3..xux .....&#xt ♦  0  0  3  3  6 |  0  0  0  0  3  3  6  3  3 | 0 0  0  0  0 1  3  3 1 0 | * * * 8 *
....x3....x4....o     ♦  0  0  0  0 24 |  0  0  0  0  0  0  0 12 24 | 0 0  0  0  0 0  0  0 8 6 | * * * * 1

or
o....3o....4o....      & | 48  *  * |  1  2  1  0  0 |  2  1  1  2  0 0 | 1  2 1
.o...3.o...4.o...      & |  * 24  * |  0  0  2  2  0 |  0  0  1  4  1 0 | 0  2 2
..o..3..o..4..o..        |  *  * 24 |  0  0  0  2  2 |  0  0  0  4  1 1 | 0  2 2
-------------------------+----------+----------------+------------------+-------
x.... ..... .....      & |  2  0  0 | 24  *  *  *  * |  2  0  1  0  0 0 | 1  2 0
..... x.... .....      & |  2  0  0 |  * 48  *  *  * |  1  1  0  1  0 0 | 1  1 1
oo...3oo...4oo...&#x   & |  1  1  0 |  *  * 48  *  * |  0  0  1  2  0 0 | 0  2 1
.oo..3.oo..4.oo..&#x   & |  0  1  1 |  *  *  * 48  * |  0  0  0  2  1 0 | 0  1 2
..... ..x.. .....        |  0  0  2 |  *  *  *  * 24 |  0  0  0  2  0 1 | 0  2 1
-------------------------+----------+----------------+------------------+-------
x....3x.... .....      & |  6  0  0 |  3  3  0  0  0 | 16  *  *  *  * * | 1  1 0
..... x....4o....      & |  4  0  0 |  0  4  0  0  0 |  * 12  *  *  * * | 1  0 1
xo... ..... .....&#x   & |  2  1  0 |  1  0  2  0  0 |  *  * 24  *  * * | 0  2 0
..... xux.. .....&#xt  & |  2  2  2 |  0  1  2  2  1 |  *  *  * 48  * * | 0  1 1
..... ..... .oqo.&#xt    |  0  2  2 |  0  0  0  4  0 |  *  *  *  * 12 * | 0  0 2
..o..3..x.. .....        |  0  0  3 |  0  0  0  0  3 |  *  *  *  *  * 8 | 0  2 0
-------------------------+----------+----------------+------------------+-------
x....3x....4o....      & ♦ 24  0  0 | 12 24  0  0  0 |  8  6  0  0  0 0 | 2  * *
xoo..3xux.. .....&#xt  & ♦  6  3  3 |  3  3  6  3  3 |  1  0  3  3  0 1 | * 16 *
..... xuxux4ooqoo&#xt    ♦  8  8  8 |  0  8  8 16  4 |  0  2  0  8  4 0 | *  * 6

xxuxoo3xuxxux3ooxuxx&#xt   → all heights = 1/sqrt(2) = 0.707107
(tut || pseudo (x,u)-tut || pseudo (u,x,x)-toe || pseudo inv (u,x,x)-toe || pseudo inv (x,u)-tut || inv tut)

o.....3o.....3o.....     | 12  *  *  *  *  * | 1  2  1 0  0  0  0  0  0  0  0 0  0  0 0 | 2 1 1  2  0  0 0  0  0 0  0  0 0 0 0 | 1 1 2 0 0 0 0
.o....3.o....3.o....     |  * 12  *  *  *  * | 0  0  1 1  2  0  0  0  0  0  0 0  0  0 0 | 0 0 1  2  1  2 0  0  0 0  0  0 0 0 0 | 0 1 2 1 0 0 0
..o...3..o...3..o...     |  *  * 24  *  *  * | 0  0  0 0  1  1  1  1  0  0  0 0  0  0 0 | 0 0 0  1  1  1 1  1  1 0  0  0 0 0 0 | 0 1 1 1 1 0 0
...o..3...o..3...o..     |  *  *  * 24  *  * | 0  0  0 0  0  0  0  1  1  1  1 0  0  0 0 | 0 0 0  0  0  1 0  1  1 1  1  1 0 0 0 | 0 0 1 1 1 1 0
....o.3....o.3....o.     |  *  *  *  * 12  * | 0  0  0 0  0  0  0  0  0  0  2 1  1  0 0 | 0 0 0  0  0  0 0  0  2 0  1  2 1 0 0 | 0 0 0 1 2 1 0
.....o3.....o3.....o     |  *  *  *  *  * 12 | 0  0  0 0  0  0  0  0  0  0  0 0  1  2 1 | 0 0 0  0  0  0 0  0  0 0  0  2 1 1 2 | 0 0 0 0 2 1 1
-------------------------+-------------------+------------------------------------------+--------------------------------------+--------------
x..... ...... ......     |  2  0  0  0  0  0 | 6  *  * *  *  *  *  *  *  *  * *  *  * * | 2 0 1  0  0  0 0  0  0 0  0  0 0 0 0 | 1 0 2 0 0 0 0
...... x..... ......     |  2  0  0  0  0  0 | * 12  * *  *  *  *  *  *  *  * *  *  * * | 1 1 0  1  0  0 0  0  0 0  0  0 0 0 0 | 1 1 1 0 0 0 0
oo....3oo....3oo....&#x  |  1  1  0  0  0  0 | *  * 12 *  *  *  *  *  *  *  * *  *  * * | 0 0 1  2  0  0 0  0  0 0  0  0 0 0 0 | 0 1 2 0 0 0 0
.x.... ...... ......     |  0  2  0  0  0  0 | *  *  * 6  *  *  *  *  *  *  * *  *  * * | 0 0 1  0  0  2 0  0  0 0  0  0 0 0 0 | 0 0 2 1 0 0 0
.oo...3.oo...3.oo...&#x  |  0  1  1  0  0  0 | *  *  * * 24  *  *  *  *  *  * *  *  * * | 0 0 0  1  1  1 0  0  0 0  0  0 0 0 0 | 0 1 1 1 0 0 0
...... ..x... ......     |  0  0  2  0  0  0 | *  *  * *  * 12  *  *  *  *  * *  *  * * | 0 0 0  1  0  0 1  1  0 0  0  0 0 0 0 | 0 1 1 0 1 0 0
...... ...... ..x...     |  0  0  2  0  0  0 | *  *  * *  *  * 12  *  *  *  * *  *  * * | 0 0 0  0  1  0 1  0  1 0  0  0 0 0 0 | 0 1 0 1 1 0 0
..oo..3..oo..3..oo..&#x  |  0  0  1  1  0  0 | *  *  * *  *  *  * 24  *  *  * *  *  * * | 0 0 0  0  0  1 0  1  1 0  0  0 0 0 0 | 0 0 1 1 1 0 0
...x.. ...... ......     |  0  0  0  2  0  0 | *  *  * *  *  *  *  * 12  *  * *  *  * * | 0 0 0  0  0  1 0  0  0 1  1  0 0 0 0 | 0 0 1 1 0 1 0
...... ...x.. ......     |  0  0  0  2  0  0 | *  *  * *  *  *  *  *  * 12  * *  *  * * | 0 0 0  0  0  0 0  1  0 1  0  1 0 0 0 | 0 0 1 0 1 1 0
...oo.3...oo.3...oo.&#x  |  0  0  0  1  1  0 | *  *  * *  *  *  *  *  *  * 24 *  *  * * | 0 0 0  0  0  0 0  0  1 0  1  1 0 0 0 | 0 0 0 1 1 1 0
...... ...... ....x.     |  0  0  0  0  2  0 | *  *  * *  *  *  *  *  *  *  * 6  *  * * | 0 0 0  0  0  0 0  0  2 0  0  0 1 0 0 | 0 0 0 1 2 0 0
....oo3....oo3....oo&#x  |  0  0  0  0  1  1 | *  *  * *  *  *  *  *  *  *  * * 12  * * | 0 0 0  0  0  0 0  0  0 0  0  2 1 0 0 | 0 0 0 0 2 1 0
...... .....x ......     |  0  0  0  0  0  2 | *  *  * *  *  *  *  *  *  *  * *  * 12 * | 0 0 0  0  0  0 0  0  0 0  0  1 0 1 1 | 0 0 0 0 1 1 1
...... ...... .....x     |  0  0  0  0  0  2 | *  *  * *  *  *  *  *  *  *  * *  *  * 6 | 0 0 0  0  0  0 0  0  0 0  0  0 1 0 2 | 0 0 0 0 2 0 1
-------------------------+-------------------+------------------------------------------+--------------------------------------+--------------
x.....3x..... ......     |  6  0  0  0  0  0 | 3  3  0 0  0  0  0  0  0  0  0 0  0  0 0 | 4 * *  *  *  * *  *  * *  *  * * * * | 1 0 1 0 0 0 0
...... x.....3o.....     |  3  0  0  0  0  0 | 0  3  0 0  0  0  0  0  0  0  0 0  0  0 0 | * 4 *  *  *  * *  *  * *  *  * * * * | 1 1 0 0 0 0 0
xx.... ...... ......&#x  |  2  2  0  0  0  0 | 1  0  2 1  0  0  0  0  0  0  0 0  0  0 0 | * * 6  *  *  * *  *  * *  *  * * * * | 0 0 2 0 0 0 0
...... xux... ......&#xt |  2  2  2  0  0  0 | 0  1  2 0  2  1  0  0  0  0  0 0  0  0 0 | * * * 12  *  * *  *  * *  *  * * * * | 0 1 1 0 0 0 0
...... ...... .ox...&#x  |  0  1  2  0  0  0 | 0  0  0 0  2  0  1  0  0  0  0 0  0  0 0 | * * *  * 12  * *  *  * *  *  * * * * | 0 1 0 1 0 0 0
.xux.. ...... ......&#xt |  0  2  2  2  0  0 | 0  0  0 1  2  0  0  2  1  0  0 0  0  0 0 | * * *  *  * 12 *  *  * *  *  * * * * | 0 0 1 1 0 0 0
...... ..x...3..x...     |  0  0  6  0  0  0 | 0  0  0 0  0  3  3  0  0  0  0 0  0  0 0 | * * *  *  *  * 4  *  * *  *  * * * * | 0 1 0 0 1 0 0
...... ..xx.. ......&#x  |  0  0  2  2  0  0 | 0  0  0 0  0  1  0  2  0  1  0 0  0  0 0 | * * *  *  *  * * 12  * *  *  * * * * | 0 0 1 0 1 0 0
...... ...... ..xux.&#xt |  0  0  2  2  2  0 | 0  0  0 0  0  0  1  2  0  0  2 1  0  0 0 | * * *  *  *  * *  * 12 *  *  * * * * | 0 0 0 1 1 0 0
...x..3...x.. ......     |  0  0  0  6  0  0 | 0  0  0 0  0  0  0  0  3  3  0 0  0  0 0 | * * *  *  *  * *  *  * 4  *  * * * * | 0 0 1 0 0 1 0
...xo. ...... ......&#x  |  0  0  0  2  1  0 | 0  0  0 0  0  0  0  0  1  0  2 0  0  0 0 | * * *  *  *  * *  *  * * 12  * * * * | 0 0 0 1 0 1 0
...... ...xux ......&#xt |  0  0  0  2  2  2 | 0  0  0 0  0  0  0  0  0  1  2 0  2  1 0 | * * *  *  *  * *  *  * *  * 12 * * * | 0 0 0 0 1 1 0
...... ...... ....xx&#x  |  0  0  0  0  2  2 | 0  0  0 0  0  0  0  0  0  0  0 1  2  0 1 | * * *  *  *  * *  *  * *  *  * 6 * * | 0 0 0 0 2 0 0
.....o3.....x ......     |  0  0  0  0  0  3 | 0  0  0 0  0  0  0  0  0  0  0 0  0  3 0 | * * *  *  *  * *  *  * *  *  * * 4 * | 0 0 0 0 0 1 1
...... .....x3.....x     |  0  0  0  0  0  6 | 0  0  0 0  0  0  0  0  0  0  0 0  0  3 3 | * * *  *  *  * *  *  * *  *  * * * 4 | 0 0 0 0 1 0 1
-------------------------+-------------------+------------------------------------------+--------------------------------------+--------------
x.....3x.....3o.....     ♦ 12  0  0  0  0  0 | 6 12  0 0  0  0  0  0  0  0  0 0  0  0 0 | 4 4 0  0  0  0 0  0  0 0  0  0 0 0 0 | 1 * * * * * *
...... xux...3oox...&#xt ♦  3  3  6  0  0  0 | 0  3  3 0  6  3  3  0  0  0  0 0  0  0 0 | 0 1 0  3  3  0 1  0  0 0  0  0 0 0 0 | * 4 * * * * *
xxux..3xuxx.. ......&#xt ♦  6  6  6  6  0  0 | 3  3  6 3  6  3  0  6  3  3  0 0  0  0 0 | 1 0 3  3  0  3 0  3  0 1  0  0 0 0 0 | * * 4 * * * *
.xuxo. ...... .oxux.&#xt ♦  0  2  4  4  2  0 | 0  0  0 1  4  0  2  4  2  0  4 1  0  0 0 | 0 0 0  0  4  4 0  0  4 0  4  0 0 0 0 | * * * 6 * * *
...... ..xxux3..xuxx&#xt ♦  0  0  6  6  6  6 | 0  0  0 0  0  3  3  6  0  3  6 3  6  3 3 | 0 0 0  0  0  0 1  3  3 0  0  3 3 0 1 | * * * * 4 * *
...xoo3...xux ......&#xt ♦  0  0  0  6  3  3 | 0  0  0 0  0  0  0  0  3  3  6 0  3  3 0 | 0 0 0  0  0  0 0  0  0 1  3  3 0 1 0 | * * * * * 4 *
.....o3.....x3.....x     ♦  0  0  0  0  0 12 | 0  0  0 0  0  0  0  0  0  0  0 0  0 12 6 | 0 0 0  0  0  0 0  0  0 0  0  0 0 4 4 | * * * * * * 1

or
o.....3o.....3o.....      & | 24  *  * |  1  2  1  0  0  0  0  0 | 2 1  1  2  0  0 0  0 | 1 1 2 0
.o....3.o....3.o....      & |  * 24  * |  0  0  1  1  2  0  0  0 | 0 0  1  2  1  2 0  0 | 0 1 2 1
..o...3..o...3..o...      & |  *  * 48 |  0  0  0  0  1  1  1  1 | 0 0  0  1  1  2 1  1 | 0 1 2 1
----------------------------+----------+-------------------------+----------------------+--------
x..... ...... ......      & |  2  0  0 | 12  *  *  *  *  *  *  * | 2 0  1  0  0  0 0  0 | 1 0 2 0
...... x..... ......      & |  2  0  0 |  * 24  *  *  *  *  *  * | 1 1  0  1  0  0 0  0 | 1 1 1 0
oo....3oo....3oo....&#x   & |  1  1  0 |  *  * 24  *  *  *  *  * | 0 0  1  2  0  0 0  0 | 0 1 2 0
.x.... ...... ......      & |  0  2  0 |  *  *  * 12  *  *  *  * | 0 0  1  0  0  2 0  0 | 0 0 2 1
.oo...3.oo...3.oo...&#x   & |  0  1  1 |  *  *  *  * 48  *  *  * | 0 0  0  1  1  1 0  0 | 0 1 1 1
...... ..x... ......      & |  0  0  2 |  *  *  *  *  * 24  *  * | 0 0  0  1  0  0 1  1 | 0 1 2 0
...... ...... ..x...      & |  0  0  2 |  *  *  *  *  *  * 24  * | 0 0  0  0  1  1 1  0 | 0 1 1 1
..oo..3..oo..3..oo..&#x     |  0  0  2 |  *  *  *  *  *  *  * 24 | 0 0  0  0  0  2 0  1 | 0 0 2 1
----------------------------+----------+-------------------------+----------------------+--------
x.....3x..... ......      & |  6  0  0 |  3  3  0  0  0  0  0  0 | 8 *  *  *  *  * *  * | 1 0 1 0
...... x.....3o.....      & |  3  0  0 |  0  3  0  0  0  0  0  0 | * 8  *  *  *  * *  * | 1 1 0 0
xx.... ...... ......&#x   & |  2  2  0 |  1  0  2  1  0  0  0  0 | * * 12  *  *  * *  * | 0 0 2 0
...... xux... ......&#xt  & |  2  2  2 |  0  1  2  0  2  1  0  0 | * *  * 24  *  * *  * | 0 1 1 0
...... ...... .ox...&#x   & |  0  1  2 |  0  0  0  0  2  0  1  0 | * *  *  * 24  * *  * | 0 1 0 1
.xux.. ...... ......&#xt  & |  0  2  4 |  0  0  0  1  2  0  1  2 | * *  *  *  * 24 *  * | 0 0 1 1
...... ..x...3..x...      & |  0  0  6 |  0  0  0  0  0  3  3  0 | * *  *  *  *  * 8  * | 0 1 1 0
...... ..xx.. ......&#x     |  0  0  4 |  0  0  0  0  0  2  0  2 | * *  *  *  *  * * 12 | 0 0 2 0
----------------------------+----------+-------------------------+----------------------+--------
x.....3x.....3o.....      & ♦ 12  0  0 |  6 12  0  0  0  0  0  0 | 4 4  0  0  0  0 0  0 | 2 * * *
...... xux...3oox...&#xt  & ♦  3  3  6 |  0  3  3  0  6  3  3  0 | 0 1  0  3  3  0 1  0 | * 8 * *
xxux..3xuxx.. ......&#xt  & ♦  6  6 12 |  3  3  6  3  6  6  3  6 | 1 0  3  3  0  3 1  3 | * * 8 *
.xuxo. ...... .oxux.&#xt    ♦  0  4  8 |  0  0  0  2  8  0  4  4 | 0 0  0  0  4  4 0  0 | * * * 6

top of page