See Takana. The 306 figures shown there can be reduced to 45 by rotation and reflection. I fitted a polynomial curve to each partial path, and superimposed them.
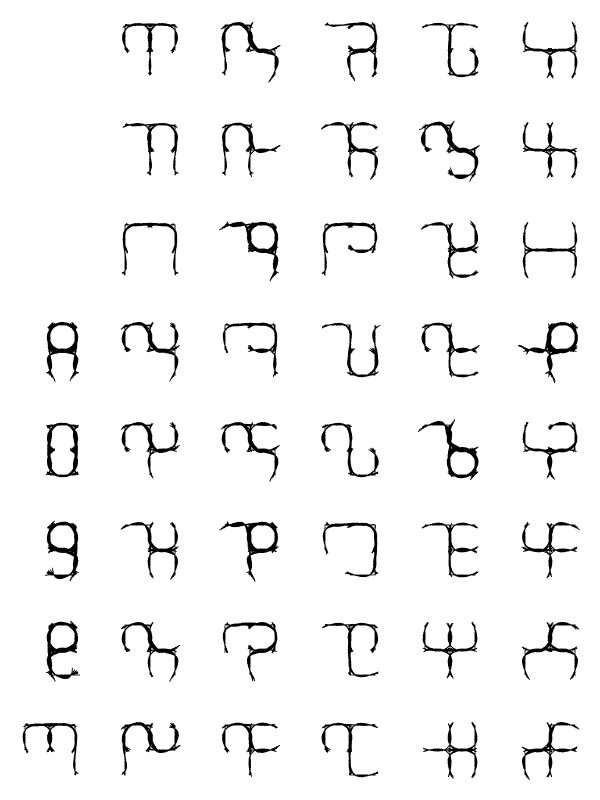
 I had the idea to design a fantasy script from combinations of a small repertoire of features: namely, subsets of this set of twelve segments. Using a fixed number of segments gives some built-in error-detection. There are 924 subsets of six segments; discarding those that form disconnected graphs leaves 306, more than enough for a syllabary. (Syllabaries have been invented more often than other types of scripts, but they’re underrepresented in fantasy.) ( . . more . . )
I had the idea to design a fantasy script from combinations of a small repertoire of features: namely, subsets of this set of twelve segments. Using a fixed number of segments gives some built-in error-detection. There are 924 subsets of six segments; discarding those that form disconnected graphs leaves 306, more than enough for a syllabary. (Syllabaries have been invented more often than other types of scripts, but they’re underrepresented in fantasy.) ( . . more . . )
Scribbles: The Ensmoothening, Part III
Many of the curves in this chart have some unsightly wiggles. That’s because, when a function of degree 2 or higher tries to approximate a piecewise constant, it tends to go back and forth across the target. So here instead I fitted each such function not to the piecewise constant directly but to the fit of the next lower degree.
( . . more . . )
Scribbles: The Ensmoothening, Part II
One thing I noticed in that last series of charts is that more than one degree of discontinuity doesn’t help: the best-looking curves are mostly on the diagonal, where only the last nonzero derivative is discontinuous. Here, therefore, are those curves all together.
In column zero, the tangent angle is piecewise constant; in column one, it is a piecewise linear function of path length, resulting in six circular arcs; in column two it is piecewise quadratic, resulting in six clothoid arcs with continuous curvature; and so on.
Of course the arcs are approximated by cubics; to improve the match, I put a knot wherever any derivative crosses zero, as well as at the discontinuities. (See the knots.)
Presented for your consideration: the somewhat disappointing results of an experiment in using piecewise polynomial spirals, of varying degrees of continuity, to fit the Takana — disappointing in that few if any of the curves are as pretty as I hoped.
I treat here only those that can be drawn with a single stroke. (The others can be built by combining subsets of these strokes.) In each chart, the degree of continuity increases downward, and the degree of the polynomials increases to the right.
A polynomial spiral is a curve whose tangent angle is a polynomial function of arc length; it has the form integral(exp(i*f(t))). (I implement it as a Taylor series.) In principle, f could be any real-valued function. If f is constant, you get a straight line; if f is linear (leftmost column in these small charts), you get a circle; if f is quadratic, you get an Euler spiral or Cornu spiral or clothoid, which is much used in railroads and highways to avoid sudden changes in lateral acceleration.
Here f is a least-squares fit to the step function which is the direction of the squared stroke. The top row of the chart shows continuity of degree zero: the component arcs meet, but that’s all; f is discontinuous. Degree one: the tangent angle is a continuous function of arc length. Degree two: the first derivative of tangent angle with respect to arc length, i.e. the curvature, is continuous. Degree n: the (n-1)th derivative of tangent angle, i.e. the (n-2)th derivative of curvature, is continuous.
Click each chart to extend it.
Later: I have come to a couple of conclusions. In most of these charts, the best entry to my eye is where f is piecewise quadratic with one continuous derivative. More than one degree of polynomial above the continuous degree adds little fidelity and detracts from beauty.