Quasiperiodic Tesselations

• Quasiperiodicity & Quasicrystals
• Projection Methods

Quasiperiodicity  &  Quasicrystals   (up)

Both, quasiperiodicity and almost periodicity, were introduced in the theory on corresponding functions by the mathematician Harald Bohr (brother of physicist Nils Bohr) in his articles "Zur Theorie der fastperiodischen Funktionen." (On the Theory of Almost Periodic Functions – 1925-1926). There he also outlines their relation to embeddings into higher dimensional spaces in such a way, that these functions, accordingly to be continued there, would become periodic again. In fact, quasiperiodicity lives on a dense modul of finite rang, while almost periodicity lives on a dense modul of infinite rang. The dense moduls then are derived as the projections of higher dimensional (periodic) lattices of spaces, such that their respective dimensions correspond to the rang of those modules (or potentially even higher, when coincident projection points would be allowed). – But after that first treatise this topic then became rather quiet.

In the mid 80th of last century quasiperiodicity got some revival. Based on the find of R. Penrose already within the 70th, both mathematics and mathematical physics got beware of, esp. as in its sequel the then so called quasicrystals had been found. D. Shechtman et al. produced a fast cooled Al-Mn alloy, which showed an icosahedrally symmetrical diffrection spectrum with very sharp peaks. – Such sharp peaks in crystallography so far were known from periodic structures only, but that symmetry for sure does not allow for such a symmetry arrangement. (That sample furthermore disproved to be a twin, i.e. a crystalline structure with macroscopical regions, each being periodic on its own, but mutually being arranged such that the overall integrated effects become as desired, similar as can be achieved in compound polytopes.) Thus these finds finally provided a change of paradigms in crystallography, now allowing for quasiperiodic structures as well.

• H. Bohr, Zur Theorie der fastperiodischen Funktionen. I. Teil: Eine Verallgemeinerung der Theorie der Fourierreihen – (On the Theory of Almost Periodic Functions. Issue I: A Generalisation of the Theory of Fourier Series), Acta Math., vol. 45 (1925), pp. 29–127
• H. Bohr, Zur Theorie der fastperiodischen Funktionen. II. Teil: Zusammenhang der fastperiodischen Funktionen mit funktionen von unendlich vielen Variablen – (Issue II: Relationship between Almost Periodic Functions and Functions of Infinitely Many Variables), Acta Math., vol. 46 (1925), pp. 101-214
• H. Bohr, Zur Theorie der fastperiodischen Funktionen. III. Teil: Dirichletentwicklung analytischer Funktionen – (Issue III: Dirichlet Series of Analytical Functions), Acta Math., vol. 47 (1926), pp. 237-281
• R. Penrose, The role of aesthetics in pure and applied mathematical research, Bull. Inst. Math. Appl., Southend-on-Sea, vol. 10 (1974), pp. 266–271
• R. Penrose, Pentaplexity - A Class of Non-Periodic Tilings of the Plane, The Mathematical Intelligencer, vol. 2, nr. 1, Springer (1979), pp. 32–37
• D. Shechtman, I. Blech, D. Gratias, J. Cahn, Metallic Phase with Long-Range Orientational Order and No Translational Symmetry, Physical Review Letters 53, vol. 20 (1984), pp. 1951-1953

Different Projection Methods   (up)

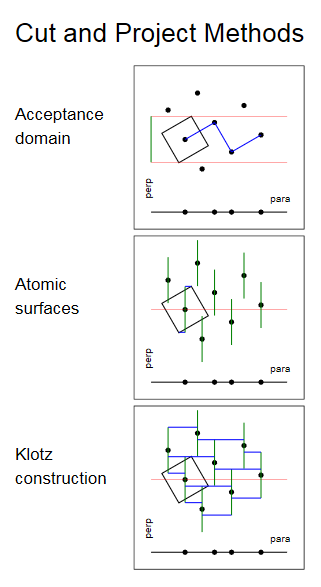
Within projection methods, or more precisely cut and project methods, the derivation of quasiperiodic tesselations is derived from (periodic) lattices, or for that purpose likewise periodic honeycombs, of some higher dimensional embedding space. The tesselation space itself then becomes some irrationally oblique subspace therof, such that the lattice points (i.e. the vertex set of the honeycomb) would project dense onto that "para space". In order to have non-infinitesimal tiles, the "perp space" will not be left unbounded, it rather gets restricted to some acceptance domain. Obviously the same result is being obtained, when point-inverted copies of that acceptance domain would be attached to the lattice points in a sense of their atomic surfaces. Then a point will be projected whenever its atomic surface would be hit by "the" para space (now being understood as some specific parallel to the tesselation subspace).

Both above methods would result within a point set only, providing the projection images of lattice points (or those of vertices) alone. In contrast to those the Klotz construction also derives the full incidence structure of tesselation space as well. To that purpose one considers 2 mutually dual high dimensional tesselations of embedding space, most often the Voronoi complex of the lattice (those hypercells then are those regions of points which are closer to the chosen lattice point than to any different one), and its dual Delone (or Delaunay) complex. One then projects the Voronoi cell onto perp space, using it for acceptance domain, and projects then the elements of according Delone cells onto tesselation space or, the other way round, uses a full set of Delone cells for projection onto perp space and the dual elements of the Voronoi cell for projection onto tesselation space. To that purpose, in either of these, briquets (german: Klotz) are built from co-dimensional elements each. I.e. the acceptance domain for lattice points (being projected down to tesselation vertices) would be the perp space projection of whole corresponding dual full-dimensional solid. And further any k-dimensional element of one complex will be projected into tesselation space whenever the perp space projection of the co-dimensional mutually orthogonal element of the other complex gets hit by para space. With resp. to its application to para space k thus will be taken less or equal to the dimension of that only. – The 2D embedding space example (then producing a 1D "tiling" only), as provided to the left, would not be too striking here. But already when considering 4D embeddings, in order to produce 2D tilings, the required incidence structures become essential. Even more for 3D tesselations, then being derived from 6D embeddings.

Btw. it should be mentioned that quasiperiodic tesselations cannot be described by means of incidence matrices like the flat periodic tesselations: The Klotz constructions shows that the acceptance domain is not just a black box, but rather is to be disassembled into smaller regions, each being responsible for each of the different vertex configurations of the tesselation. This still seems to imply positiveness, but we have to take into account not only the projection onto para space (where vertices live on a dense modul, the projection of all lattice points), but onto the perp space as well. This then induces a dense projection of according atomic surfaces too. Any such now gets dissected into these smaller regions. But, because of dense perp space projections, virtually any finite region gets dissected in infinitely many infinitesimal parts. Accordingly we ought to consider infinitely many different vertex classes too. (And similar for edges, faces, etc.) Moreover, whenever the embedding was chosen to be minimal, any such class would contain just a single member each. This proves the insanity of such an attempt.

But we get an different benefit from this same consideration. Assume minimal embedding. Then the relative volume of each of the smaller regions (responsible for the different vertex configurations) provides a direct measure for the frequency of that specific vertex configuration within the tesselation!

General notation:
Let Λ be some d-dimensional lattice. Then T_Λ represents the flat d_||-dimensional tesselation obtained when the d_||-dimensional elements of the Voronoi complex V are projected into para space, and the d_⊥ = d - d_|| dimensional elements of its dual Delone complex V* into perp space. These projections then pairwise each derive a Klotz construction by simply using the corresponding cartesian products, which on its own is a further high dimensional complex. – Conversely, when using the d_|| dimensional elements of the Delone complex V* for projection in para space and the d_⊥ = d - d_|| dimensional elements of its dual Voronoi complex V = (V*)*, and applying a similar Klotz construction here, one finally derives the tesselation T*_Λ.

Names of above tilings generally are due to their first referenciations. Reproduction of those by means of projection methods was done later only: according research was done by the crew around P. Kramer, Tübingen, in the early 90th. Cf. e.g. several of the authors papers of those days and references cited therein. (Within that crew the several lattices (incl. the therefrom derived quasiperiodic tesselations) were associated to the main contributors as: A₄ - M. Baake & M. Schlottmann, D₄ - D. Joseph, A₂×A₂ and A₆ - R. Klitzing, C₆ - D. Zeidler, D₆ and D₆* - Z. Papadopolos.)

The Penrose tiling well can be derived from C₅ as well. But then the embedding is not minimal. The perp space then would decompose into a 2D subspace of acceptance domains plus a further 1D periodical space. The corresponding projection then would be degenerate, reducing all that infinitude of lattice points of this direction onto a single vertex each of tiling space. This just mirrors the fact that A₄ is nothing but the intersection of C₅ with a hyperspace perpendicular to that additional 1D periodic perp space component. In fact, both otcypit and cypit happen to be just different sections of penth, being obtained respectively at intermedials (Voronoi complex) or at vertex layers (Delone complex) when taken perpendicular wrt. to the body diagonals of the pents. – For either of the Klotz constructions of A₆ a similar decomposition of perp space into 2 different 2D components takes place (and the tiling space here too is a further 2D component). Nonetheless that representation still is minimal here, no additional periodic part is being used. (A similar non-minimal embedding here might be achieved wrt. C₇, so.)