Name	Socolar tiling
Projection device	TA2×A2 The root lattice A2×A2 is provided by the vertex set of tribbit. The Voronoi complex here is hibbit and the Delone complex is tribbit.
	©
External links	quadibloc

Vertex configurations & acceptance regions

At the left the semiregular-hexagonal acceptance domain, which corresponds to the projection of a single Delone cell, which here is a triddip into the perp space. Note that this projection of a single Delone cell just has threefold symmetry. However, the chosen projection direction divides the triddips into 4 mutually different orientations, which after projection would result in the remaining three other oriented versions of that very acceptance domain, which thus in total provide an indeed twelvefold tiling. At the right the corresponding vertex configurations of the tiling space are shown. There the incident tiles are projections of the polygonal faces of the Voronoi cell, which here is a hiddip. Accordingly the tiles either are tetragons, within the chosen projection either squares or (30°,150°)-rhombs, or (fully-symmetrically projected) hexagons. Within the following table the different regions of the acceptance domain are marked in red.

When lifting the incident tiles of tiling space back into embedding space, and selecting the dual Delone cell boundary of that specific Voronoi cell boundary, the corresponding projection shadow into perp space always is shown there in rose. These acceptance domains of tiles also are labeled accordingly by "T" (for hexagons, having regular triangle domains), "S" (for squares) resp. "R" (for rhombs). Obviously the red regions are just the common intersections each of those rosaic tile domains. Btw., the prism products of alike marked regions of tiling space (tiles) and of perp space (their acceptance domains) happens to be the corresponding Klotz.

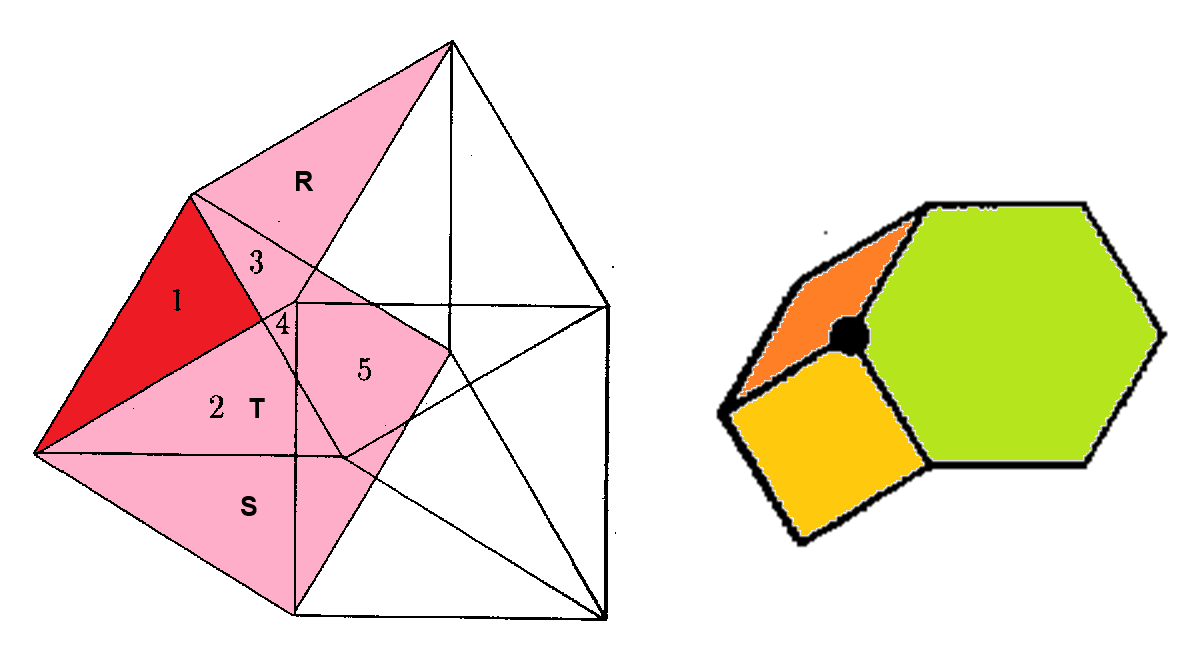Type 1 relative frequency = [sqrt(3)-1]/32 = 2.287659 % count of orientations = 24	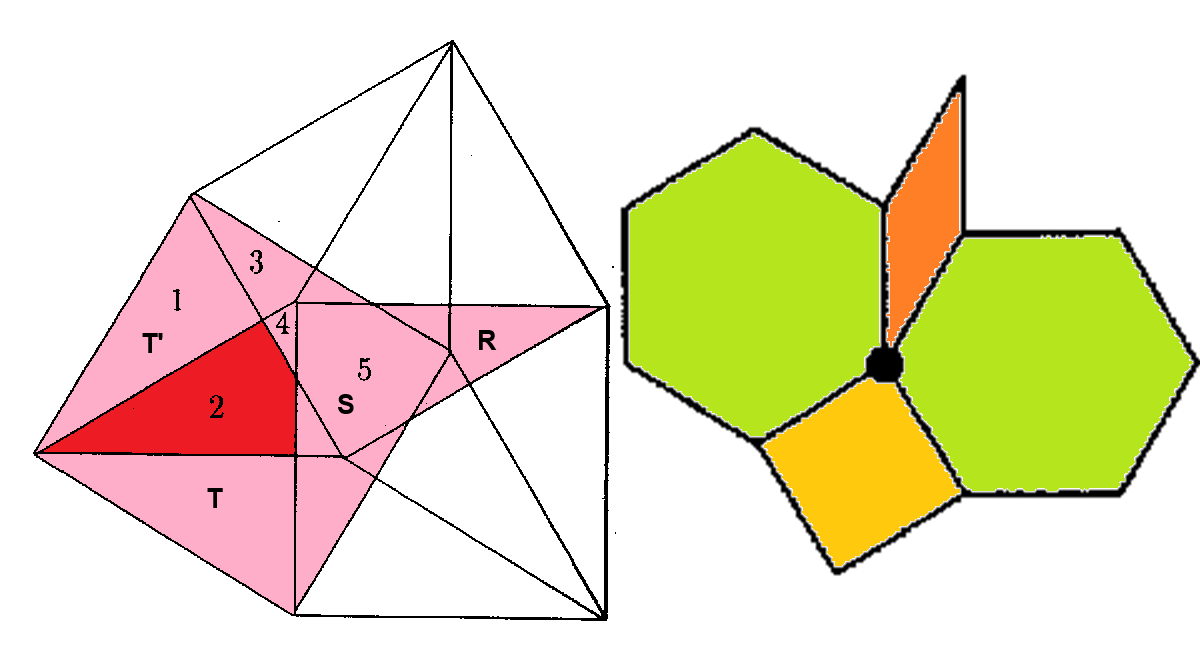Type 2 relative frequency = [9-5 sqrt(3)]/16 = 2.123412 % count of orientations = 12
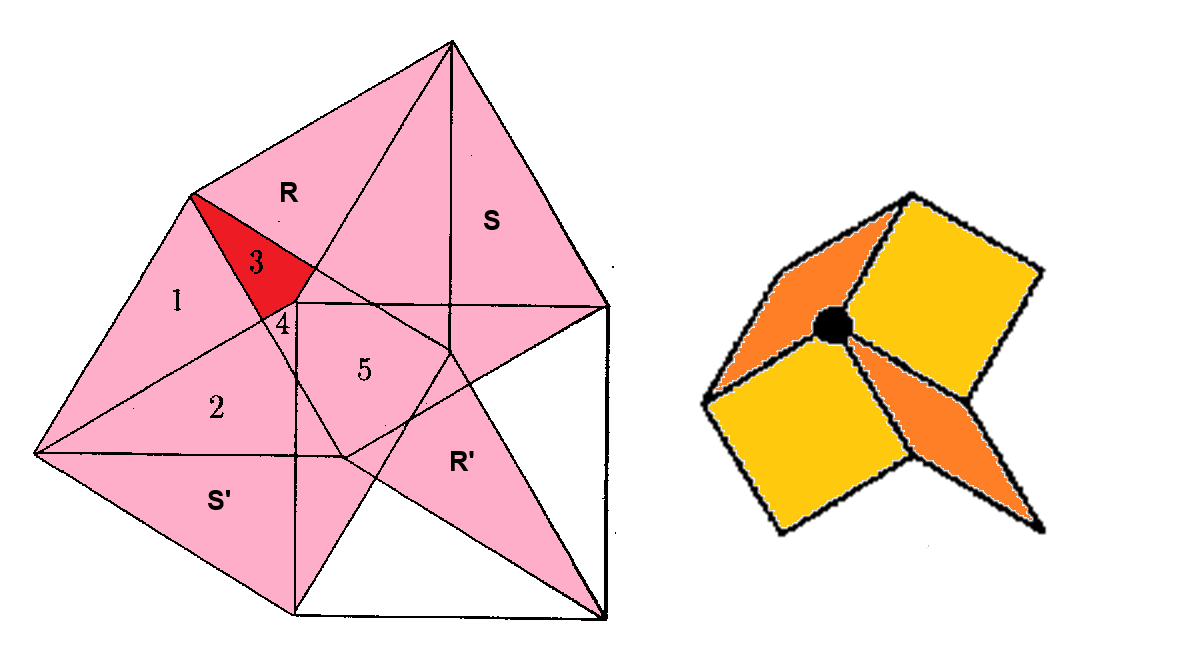Type 3 relative frequency = [9-5 sqrt(3)]/48 = 0.707804 % count of orientations = 12	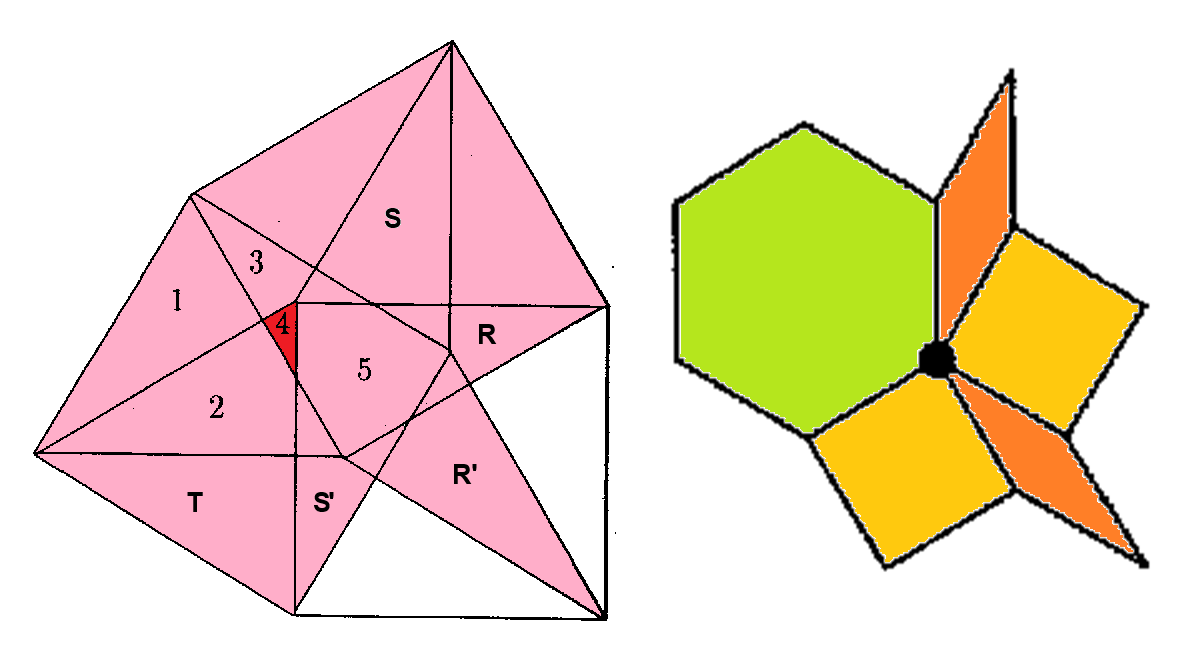Type 4 relative frequency = [11 sqrt(3)-19]/32 = 0.164247 % count of orientations = 24
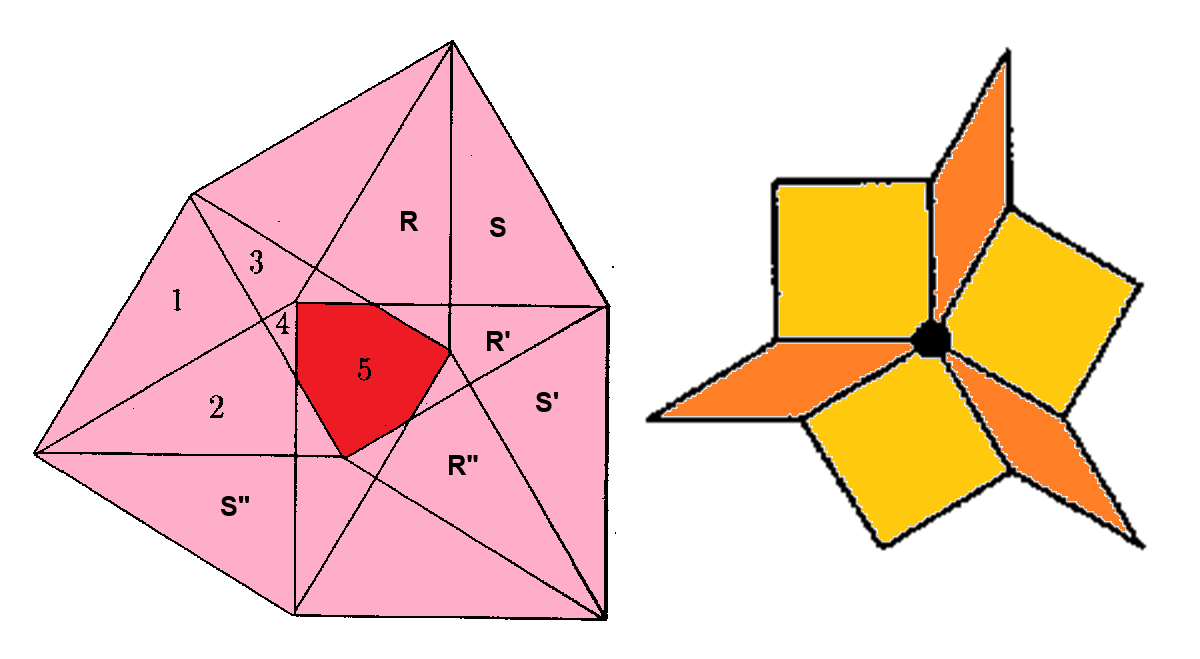Type 5 relative frequency = [7-4 sqrt(3)]/4 = 1.794919 % count of orientations = 4

Substitution

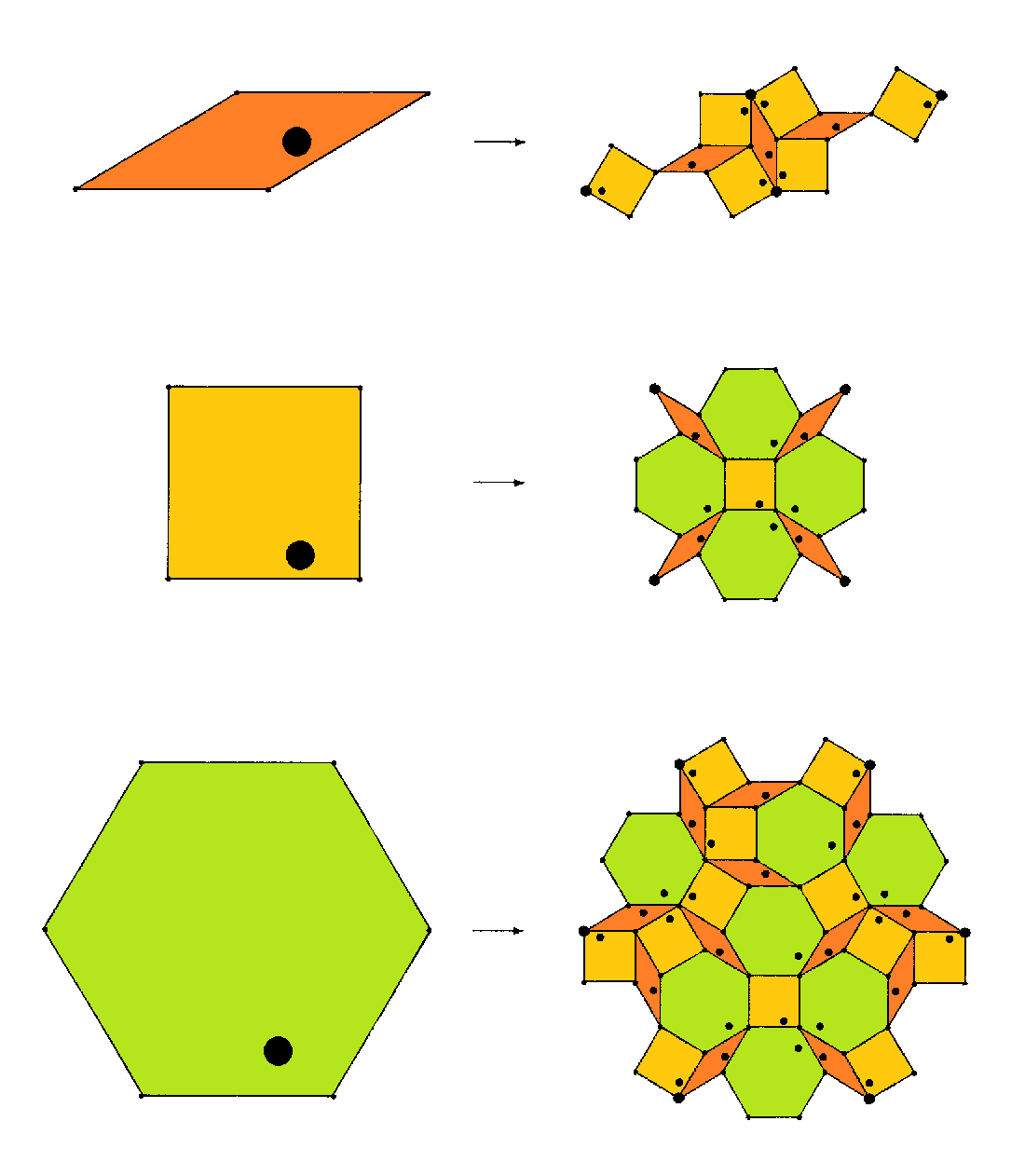
The Socolar tiling alternatively can be obtained by an iterated application of a substitution rule, which requires an additional orientation of the tiles (black dots).

The (linear) scaling factor of patch inflation then is evidently ρ = 2+sqrt(3) = 3.732051. Note that this substitution does not respect the (scaled) original outline, and thus in the below provided substitution matrix only those child tiles contribute, which have their center within the outline of the parent tile.

Substitution matrix:

3 4 12		-- child rhombs
6 1 12		-- child squares
0 4  7		-- child hexagons

| |  +-- parent hexagons
| +----- parent square
+------- parent rhomb

Matching Rules

 

The mere tiles as such clearly allow for a periodic arrangement too, cf. eg. the right example. – In order to dissallow such tilings, i.e. to enforce the here required quasiperiodic arrangement, such as already got enforced both by the projection as well as the substitution methods, one would have to apply local matching rules onto the tiles. An according such example is given below.
©