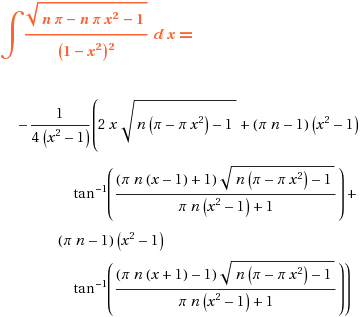Rusin’s disco ball  |
golden angles  |
Saff & Kuijlaars  |
Examples of three algorithms for distributing nodes fairly evenly over a sphere. Those on the middle and right slice the sphere into parallel bands of equal area (much narrower than the white discs), and put one node (center of a disc) somewhere in each band. Saff & Kuijlaars place the nodes along a spiral path across the bands, keeping the distance between turns of the spiral roughly constant. Failing to grok how their rule does that, I approach it from another angle.
In the ideal limit (N approaching infinity), the unit sphere is covered exactly once by a strip of width 2√(π/N) and length 2√(Nπ); the strip is divided into N nearly square pieces, with a node in the center of each. What parametric functions of -1 < t < 1 describe the midline of the strip?
(In what follows, θ and φ have their conventional meanings of longitude and co-latitude, i.e. angular distance from a pole.)
The equal slices rule gives cosφ = t. I seek a function θ(t) such that the derivative along the path has constant magnitude:
ds² = dφ² + sin²φ dθ² = Nπ dt²
I proceed:
–sinφ dφ = dt; dφ = –dt / sinφ = –dt / √(1–t²)
ds² = Nπ dt² = ( dt² / (1–t²) ) + (1–t²) dθ²
(1–t²) dθ² = dt² (Nπ – 1 / (1–t²))
= dt² (Nπ – Nπt² – 1) / (1–t²)dθ² = dt² (Nπ – Nπt² – 1) / (1–t²)²
So I ask the Wolfram Integrator to integrate
Sqrt[ n*Pi - n*Pi*x^2 - 1 ] / (1-x^2)
and it says
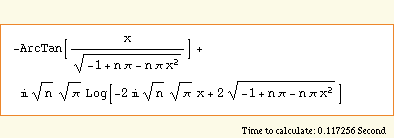
Now, I do make mistakes; I’ve worked the problem several times now and got subtly different answers. Last time around, in fact, there were no imaginary coefficients; so I made this in PoV-Ray:

Not quite what I’m looking for. Can you spot where I went wrong?
Still. Pret-ty.
one problem is that when t=±1, the integrand is undefined — it might be easier to compute dt/dθ, instead of the reciprocal
also, the square roots are problematic, since some terms are negative at t=±1: for example,
n*pi*(1-t^2)-1
is -1 when t=±1, and is positive for the midrange.
The function need not be valid all the way to the pole: I only need it for |t|≤(N-1)/N.
But never mind, it’s not a bad idea to eliminate t rather than φ. So:
. . so we integrate
Sqrt[n*Pi-csc[x]^2]and get —— not even an attempt. Wow.
Well, the point about square roots suggests that my blunder was earlier in the process.
this integral is much better, but it still needs special estimates at the boundaries (here x is phi, not t as it was in the other integral, so this integral needs to go from x=0 to x=pi, where csc[x] is infinite at both endpoints)
but it is otherwise probly ok, even if not closed form —
it is easy to show that for
|t| < 1,
we have
n > pi / (2*pi – 1) (~0.6),
and we can show that
n^2 / (2*n-1) < (n-1)/n) using a special case to avoid the weirdness in the integrals
Again, I seek an antiderivative valid for (1–N)/N ≤ t = cosφ ≤ (N–1)/N, not a definite integral from pole to pole.
Wow; what a wonderful use of both POVRay and Mathematica. (first time visitor)
Now I see one blunder: the denominator of the integrand ought to be squared! The result is still far from pretty: