There is no quick or certain algorithm to find the best arrangement of N nodes on a sphere, but here are three that may be good enough.

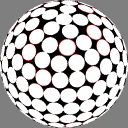
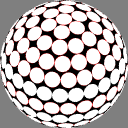
The first column shows Dave Rusin's "disco ball": place the nodes along rows equally spaced by latitude, with as many in each row as will fit at that same distance from each other. (I also show what happens if the spacing is tightened to admit at least one more node without changing the number of rows.)

The other two rules each divide the sphere into bands of equal area, and place one node at some longitude in the middle of the band.

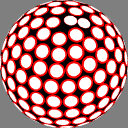
In the middle column, the longitude steps by a constant interval, a golden section of the circle. Because the golden section (sqrt(5)-1)/2 is the most irrational number, this avoids a near-repeat of the same longitude in any nearby band. (This method has been independently found by many amateurs including me.)

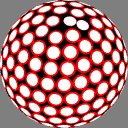
In the right column, the method of Saff and Kuijlaars places the nodes in a more obvious single spiral, making the distance between adjacent nodes approximately equal to that between successive turns of the spiral. (Note: The page cited confuses phi with theta.)

In these images the nodes are centers of white discs of equal size, chosen so that none overlap but somewhere on the sphere there is at least one point where two discs meet. The number below each image is the ratio of the diameter of the overall sphere to that of the discs.

The red rings around the white discs show the half-distance to that node's nearest neighbor. A perfectly even packing would show no red at all.

As you can see, Rusin's rule gives the densest packings, but because its anisotropy is more obvious I find it less pretty than the others; for the same reason I would not be surprised if it is less useful for some purposes.

	Rusin's disco ball	golden sector	Saff & Kuijlaars
006	1.414214 (optimal)	1.587431	1.762795
007	1.701302	1.709011	1.912087
012	2.000000	2.244487	2.529424
014	2.309401	2.424840	2.737578
020	2.613126	2.898101	3.283709
023	2.923804	3.107512	3.525160
030	3.236068	3.548099	4.032681
034	3.402603	3.776758	4.295845
044	3.863703	4.295342	4.892192
049	4.178581	4.532396	5.164602
058	4.493959	4.930419	5.621770
064	4.609530	5.178784	5.906922
078	5.125831	5.716461	6.523982
085	5.464102	5.967150	6.811580
098	5.758770	6.406732	7.315756
106	6.010855	6.662840	7.609432
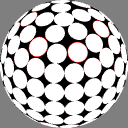
124	6.392453	7.205870	8.231983
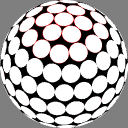
133	6.726918	7.462578	8.526229
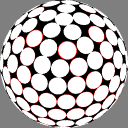
146	7.026674	7.818511	8.934159
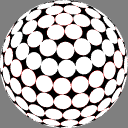
156	7.201051	8.081644	9.235698
176	7.661298	8.583742	9.811012
186	7.931559	8.824082	10.086371
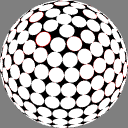
208	8.296230	9.331065	10.667169
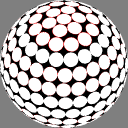
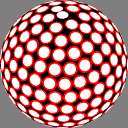
222	8.684322	9.639817	11.020843
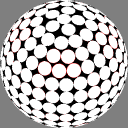
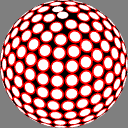
244	8.931404	10.105957	11.554764
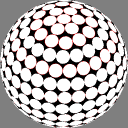
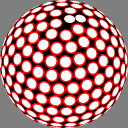
255	9.249067	10.331142	11.812679
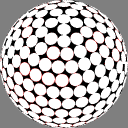
278	9.566772	10.786804	12.334540
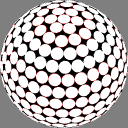
290	9.882249	11.017061	12.598236
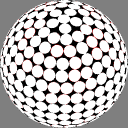
318	10.202297	11.536470	13.193047
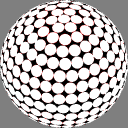
331	10.520110	11.769834	13.460278
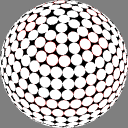
358	10.837951	12.240306	13.999004
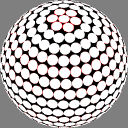
386	11.567274	12.709821	14.536611
404	11.473713	13.002702	14.871956
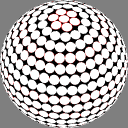
434	12.217355	13.476700	15.414662
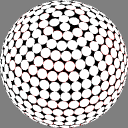
448	12.109566	13.692285	15.661490
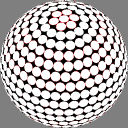
480	12.869074	14.172741	16.211562