Acronym	chic
Name	chamfered cube, octahedrally truncated rhombic dodecahedron
	©   ©
Vertex figure	[4,H2], [h3]
Coordinates	(1/2 + 1/sqrt(3), 1/2 + 1/sqrt(3), 1/2 + 1/sqrt(3))       & all changes of sign (vertex inscribed cube) (1/2, 1/2, 1/2 + 2/sqrt(3))               & all permutations, all changes of sign
General of army	(is itself convex)
Colonel of regiment	(is itself locally convex)
Dihedral angles (at margins)	between {4} and {(h,H,H)2}:   135° between {(h,H,H)2} and {(h,H,H)2}:   120°
Face vector	32, 48, 18
Confer	rad   cube   oq3oo4ux&zc
External links

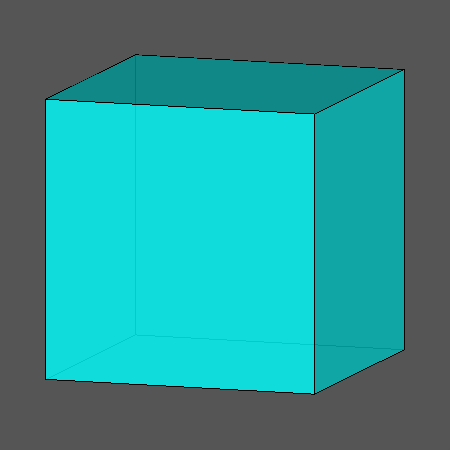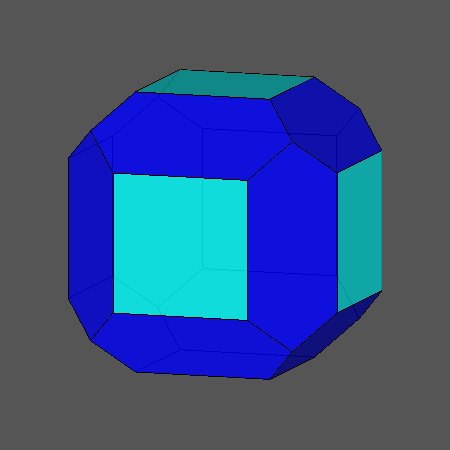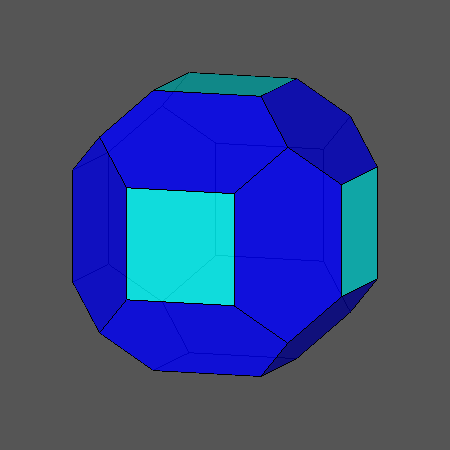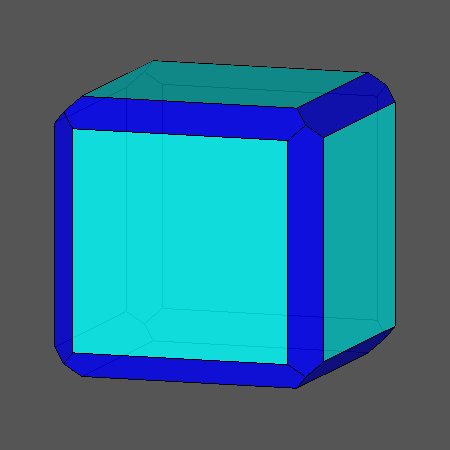
The non-regular hexagons {(h,H,H)²} have vertex angles h = arccos(-1/3) = 109.471221° resp. H = arccos[-1/sqrt(3)] = 125.264390°.

Octahedral truncation applies to the octahedral vertices (vertex inscribed oct) only. Wrt. the rad this produces new square faces there. These are then face planes of a cutting cube. – The above transition shows a dynamical mutual scaling of cube and rad. The chamfered cube then is the instance, where all edges happen to have the same length. However there also occurs a not so deep truncation as the Waterman polyhedron number 5 wrt. body-centered cubic lattice C₃* centered at a lattice point (oq3oo4ux&#zc). (Note that here the diagonals of the non-regular hexagons will not be side-parallel, while there they happen to be.)

Chamfering (or edge-only beveling – here is being applied to the cube) flatens the former edges into new (non-regular hexagonal) faces. There is a deeper, terminal chamfering of the cube too, which then reduces the original faces to nothing. Then the hexagons will become rhombs and the total figure becomes the rad. – When considering the below provided tegum sum Dynkin symbol, it becomes obvious that this figure also can be seen as a Stott expansion of the rad.

Incidence matrix according to Dynkin symbol

ax4oo3oc&#zx   → height = 0
                 a = (3+2 sqrt(3))/3 = 2.154701
                 c = sqrt(8/3) = 1.632993
(tegum sum of a-cube and (x,c)-sirco)

o.4o.3o.     | 8  * |  3  0 |  3 0  [h3]
.o4.o3.o     | * 24 |  1  2 |  2 1  [4,H2]
-------------+------+-------+-----
oo4oo3oo&#x  | 1  1 | 24  * |  2 0
.x .. ..     | 0  2 |  * 24 |  1 1
-------------+------+-------+-----
ax .. oc&#zx | 2  4 |  4  2 | 12 *  {(h,H,H)2}
.x4.o ..     | 0  4 |  0  4 |  * 6  {4}