Fractals

Fractals usually are defined via some substitution rule, thereby considering the limit of an infinite sequence of iterated application substitutions of a starting set of tiles by according patches of tiles, again individually being chosen from the same set, but scaled down by some factor ε, and which are designed such, that their overall boundary either is kept or at least is only deformed in such a way, that the substitution rule, i.e. arrangement of smaller copies within those patches still matches iteratedly.

©

Thence the easiest case of substitution rules clearly are mere subdivision rules, cf. eg. the right picture, which as such clearly still does not define a fractal. More relevant body-fractal examples can be given here by the different dimensional series of Cantor set structures given below with ε=1/3. An easy to calculate measure here is the fractal dimension D, which for non-overlapping substitution rules (such as dissections are) both coincide with Hausdorff and box counting dimensions. For mere dissections of a single tile into N ε-scaled copies of itself one simply has D = log(N)/log(1/ε). (Note, that because of taking the ratio, the concrete logarithm function does not matter, it might be lb, ln, lg,..., i.e. wrt. base 2, e, 10, or any other.)

embedding dimension	1	2	3	d
central removement	Cantor set © successiv decomposition into 31 = 3 bits: 2 outer (maintained) and 1 central (removed) D = log(2)/log(3) = 0.630930	Sierpinski carpet © successiv decomposition into 32 = 9 bits: 8 outer (maintained) and 1 central (removed) D = log(8)/log(3) = 1.892789	successiv decomposition into 33 = 27 bits: 26 outer (maintained) and 1 central (removed) D = log(26)/log(3) = 2.965647	successiv decomposition into 3d bits: 3d-1 outer (maintained) and 1 central (removed) D = log(3d-1)/log(3)
axial removement		Cantor dust © successiv decomposition into 32 = 9 bits: 32-2·2-1 = 4 outer (maintained) and 1+2·2 = 5 axial (removed) D = log(4)/log(3) = 1.261860	Menger sponge © successiv decomposition into 33 = 27 bits: 33-2·3-1 = 20 outer (maintained) and 1+2·3 = 7 axial (removed) D = log(20)/log(3) = 2.726833	successiv decomposition into 3d bits: 3d-2d-1 outer (maintained) and 1+2d axial (removed) D = log(3d-2d-1)/log(3)

 

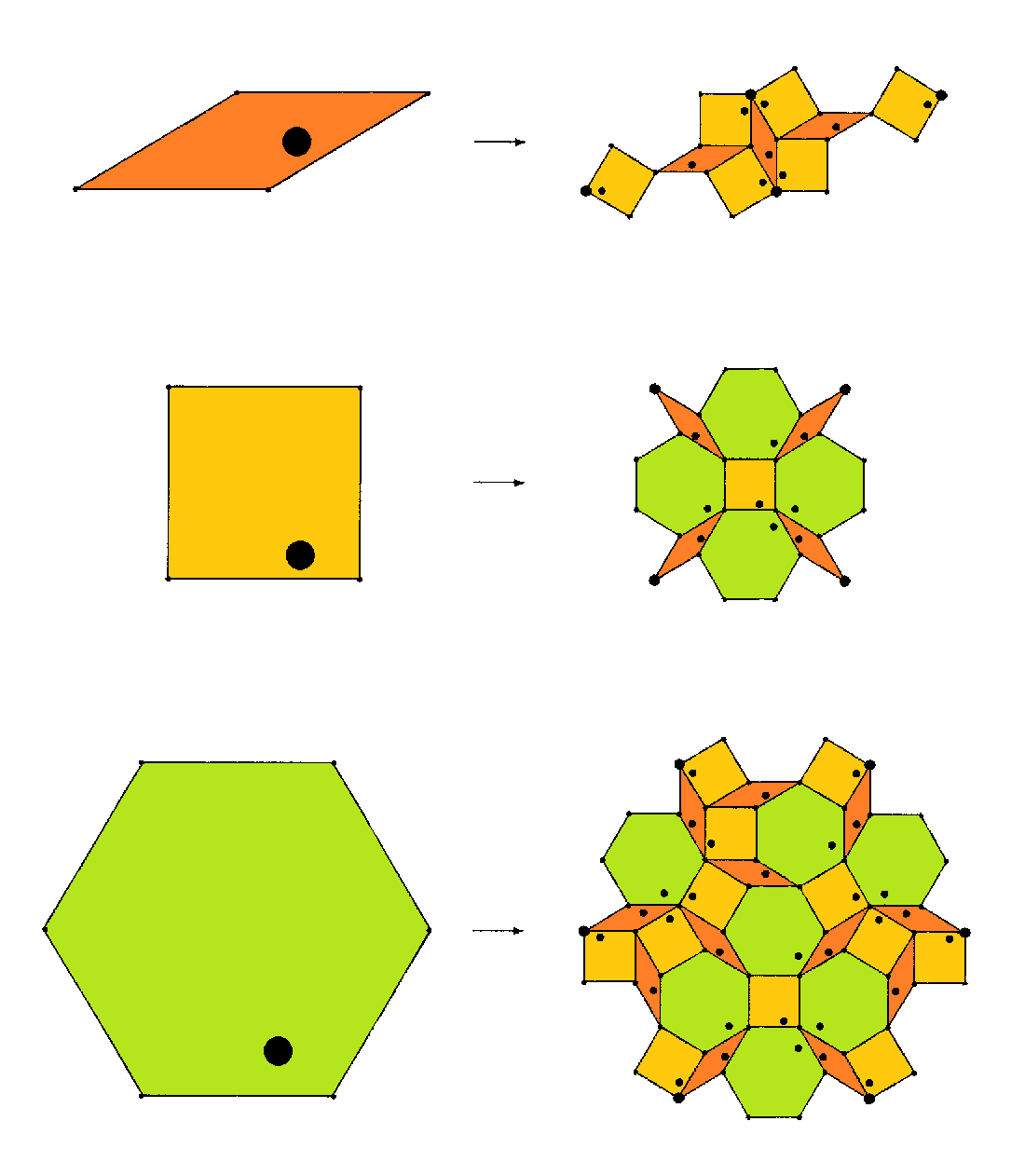
More involved substitution rules might violate the above depicted true dissection property, although still having neither gaps nor overlaps. Thence it becomes obvious that the calculation rules for fractal dimensions, as described above, still would apply, but, because of lacking any gaps, the tiles won't be body-fractals at all. However, the deviations at their borders, when counting the smaller tiles completely in/out, depending on their respective child's body-center with respect to the parents border, then would here produce ultimately a border-fractalisations of those tiles instead. Cf. e.g. the right depicted substitution rule for the Socolar tiling with its below given substitution matrix

3 4 12		-- child rhombs
6 1 12		-- child squares
0 4  7		-- child hexagons

| |  +-- parent hexagons
| +----- parent square
+------- parent rhomb

 

Obviously any patch with current tile count vector, given in this basis of rhombs, squares, hexagons respectively, when substituted iteratedly, will have an according tile count vector, when this matrix gets applied from the left. I.e. for infinite applications such initial patches become infinite tilings and the absolute tile numbers, when iteratedly renormalized by the total tile count, become according tile frequences. In here both rhombs and square have frequency (6-sqrt(3))/11 = 38.799538 %, while the hexagons have frequency (2sqrt(3)-1)/11 = 22.400924 %.

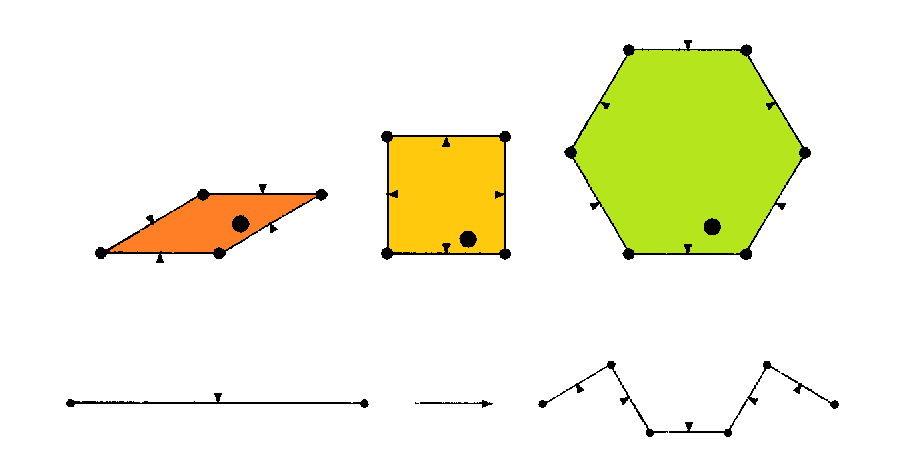
For true tile-dissecting substitutions the entries of the left eigenvector in contrast would amount in the relative tile volumes (or, within 2D: areas). For non-dissecting substitutions the step-by-step border-meandering however amounts in a fractalisation of the tile outlines. I.e. the according eigenvector entries thus provide the relative volumes of the accordingly fractalised tiles, because only then the substitution becomes again fully dissecting. Esp. in the current example the fractalised rhombs, fractalised squares, and fractalised hexagons would have a volume-ratio of (21 sqrt(3)-33)/26 = 12.973334 % to (10-4 sqrt(3))/13 = 23.629206 % to (3-sqrt(3))/2 = 63.397460 %.

The border-fractalisation, as shown on the left, uses an edge-size scaling-ratio of 1/ε = 2+sqrt(3) = 3.732051. And the scaled edge pull consists of 5 smaller ones. Thence the fractal dimension of that border here amounts in D = log(5)/log(2+sqrt(3)) = 1.222088.