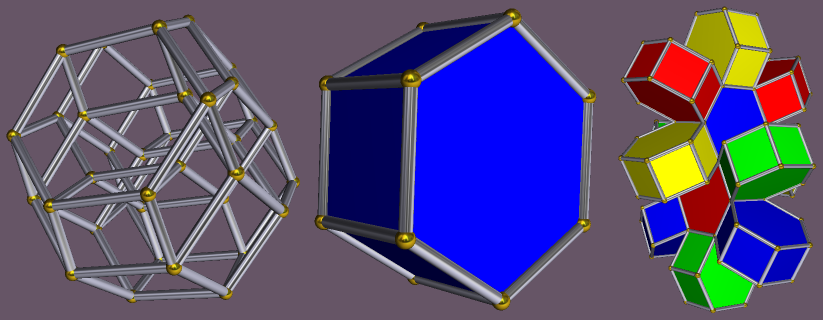
Voronoi cell of lattice A2×A2
 ©
©
©
- general duoprisms:
- 6,n-dip n,n-dip n,m-dip 2n,m-dip 2n,2m-dip
- compounds:
- affip datap
- general polytopal classes:
- Wythoffian polychora noble polytopes bistratic lace towers lace simplices
links



| Acronym | hiddip |
| Name |
hexagonal-hexagonal duoprism, Voronoi cell of lattice A2×A2 |
 © ©

| |
| Cross sections |
|
| Circumradius | sqrt(2) = 1.414214 |
| Volume | 27/4 = 6.75 |
| General of army | (is itself convex) |
| Colonel of regiment | (is itself locally convex) |
| Dihedral angles | |
| Face vector | 36, 72, 48, 12 |
| Confer |
|
|
External links |



|
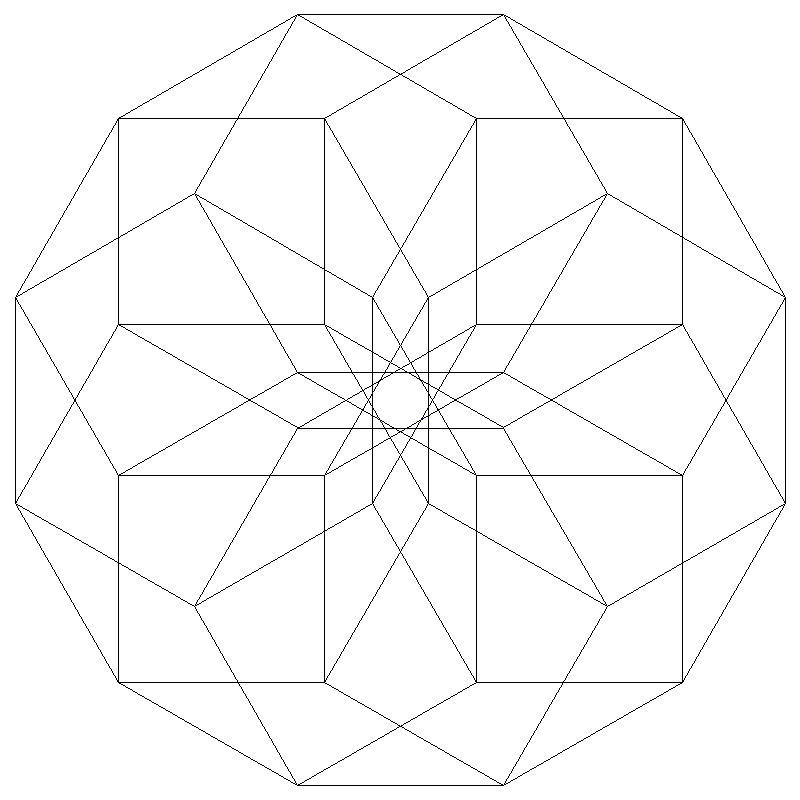
It ought be emphasized that the 4-coloring, shown in the net above, represents hiddip's representation according to x3x x3x.
It further shall be pointed out that hiddip plays the role of the acceptance domain for the quasiperiodic Stampfli tiling.
Incidence matrix according to Dynkin symbol
x6o x6o . . . . | 36 | 2 2 | 1 4 1 | 2 2 --------+----+-------+--------+---- x . . . | 2 | 36 * | 1 2 0 | 2 1 . . x . | 2 | * 36 | 0 2 1 | 1 2 --------+----+-------+--------+---- x6o . . | 6 | 6 0 | 6 * * | 2 0 x . x . | 4 | 2 2 | * 36 * | 1 1 . . x6o | 6 | 0 6 | * * 6 | 0 2 --------+----+-------+--------+---- x6o x . ♦ 12 | 12 6 | 2 6 0 | 6 * x . x6o ♦ 12 | 6 12 | 0 6 2 | * 6 snubbed forms: s6o2s6o
or . . . . | 36 | 4 | 2 4 | 4 -----------+----+----+-------+--- x . . . & | 2 | 72 | 1 2 | 3 -----------+----+----+-------+--- x6o . . & | 6 | 6 | 12 * | 2 x . x . | 4 | 4 | * 36 | 2 -----------+----+----+-------+--- x6o x . & ♦ 12 | 18 | 2 6 | 12
x3x x6o . . . . | 36 | 1 1 2 | 1 2 2 1 | 2 1 1 --------+----+----------+-----------+------ x . . . | 2 | 18 * * | 1 2 0 0 | 2 1 0 . x . . | 2 | * 18 * | 1 0 2 0 | 2 0 1 . . x . | 2 | * * 36 | 0 1 1 1 | 1 1 1 --------+----+----------+-----------+------ x3x . . | 6 | 3 3 0 | 6 * * * | 2 0 0 x . x . | 4 | 2 0 2 | * 18 * * | 1 1 0 . x x . | 4 | 0 2 2 | * * 18 * | 1 0 1 . . x6o | 6 | 0 0 6 | * * * 6 | 0 1 1 --------+----+----------+-----------+------ x3x x . ♦ 12 | 6 6 6 | 2 3 3 0 | 6 * * x . x6o ♦ 12 | 6 0 12 | 0 6 0 2 | * 3 * . x x6o ♦ 12 | 0 6 12 | 0 0 6 2 | * * 3
x3x x3x . . . . | 36 | 1 1 1 1 | 1 1 1 1 1 1 | 1 1 1 1 --------+----+-------------+-------------+-------- x . . . | 2 | 18 * * * | 1 1 1 0 0 0 | 1 1 1 0 . x . . | 2 | * 18 * * | 1 0 0 1 1 0 | 1 1 0 1 . . x . | 2 | * * 18 * | 0 1 0 1 0 1 | 1 0 1 1 . . . x | 2 | * * * 18 | 0 0 1 0 1 1 | 0 1 1 1 --------+----+-------------+-------------+-------- x3x . . | 6 | 3 3 0 0 | 6 * * * * * | 1 1 0 0 x . x . | 4 | 2 0 2 0 | * 9 * * * * | 1 0 1 0 x . . x | 4 | 2 0 0 2 | * * 9 * * * | 0 1 1 0 . x x . | 4 | 0 2 2 0 | * * * 9 * * | 1 0 0 1 . x . x | 4 | 0 2 0 2 | * * * * 9 * | 0 1 0 1 . . x3x | 6 | 0 0 3 3 | * * * * * 6 | 0 0 1 1 --------+----+-------------+-------------+-------- x3x x . ♦ 12 | 6 6 6 0 | 2 3 0 3 0 0 | 3 * * * x3x . x ♦ 12 | 6 6 0 6 | 2 0 3 0 3 0 | * 3 * * x . x3x ♦ 12 | 6 0 6 6 | 0 3 3 0 0 2 | * * 3 * . x x3x ♦ 12 | 0 6 6 6 | 0 0 0 3 3 2 | * * * 3 snubbed forms: s3s2x3x, s3s2s3s
xux xxx6ooo&#xt → both heights = sqrt(3)/2 = 0.866025 (hip || pseudo (x,u)-hip || hip) o.. o..6o.. | 12 * * | 1 2 1 0 0 0 0 | 2 1 2 1 0 0 0 0 | 1 1 2 0 0 .o. .o.6.o. | * 12 * | 0 0 1 2 1 0 0 | 0 0 2 1 1 2 0 0 | 0 1 2 1 0 ..o ..o6..o | * * 12 | 0 0 0 0 1 1 2 | 0 0 0 1 0 2 2 1 | 0 0 2 1 1 ----------------+----------+--------------------+-------------------+---------- x.. ... ... | 2 0 0 | 6 * * * * * * | 2 0 0 1 0 0 0 0 | 1 0 2 0 0 ... x.. ... | 2 0 0 | * 12 * * * * * | 1 1 1 0 0 0 0 0 | 1 1 1 0 0 oo. oo.6oo.&#x | 1 1 0 | * * 12 * * * * | 0 0 2 1 0 0 0 0 | 0 1 2 0 0 ... .x. ... | 0 2 0 | * * * 12 * * * | 0 0 1 0 1 1 0 0 | 0 1 1 1 0 .oo .oo6.oo&#x | 0 1 1 | * * * * 12 * * | 0 0 0 1 0 2 0 0 | 0 0 2 1 0 ..x ... ... | 0 0 2 | * * * * * 6 * | 0 0 0 1 0 0 2 0 | 0 0 2 0 1 ... ..x ... | 0 0 2 | * * * * * * 12 | 0 0 0 0 0 1 1 1 | 0 0 1 1 1 ----------------+----------+--------------------+-------------------+---------- x.. x.. ... | 4 0 0 | 2 2 0 0 0 0 0 | 6 * * * * * * * | 1 0 1 0 0 ... x..6o.. | 6 0 0 | 0 6 0 0 0 0 0 | * 2 * * * * * * | 1 1 0 0 0 ... xx. ...&#x | 2 2 0 | 0 1 2 1 0 0 0 | * * 12 * * * * * | 0 1 1 0 0 xux ... ...&#xt | 2 2 2 | 1 0 2 0 2 1 0 | * * * 6 * * * * | 0 0 2 0 0 ... .x.6.o. | 0 6 0 | 0 0 0 6 0 0 0 | * * * * 2 * * * | 0 1 0 1 0 ... .xx ...&#x | 0 2 2 | 0 0 0 1 2 0 1 | * * * * * 12 * * | 0 0 1 1 0 ..x ..x ... | 0 0 4 | 0 0 0 0 0 2 2 | * * * * * * 6 * | 0 0 1 0 1 ... ..x6..o | 0 0 6 | 0 0 0 0 0 0 6 | * * * * * * * 2 | 0 0 0 1 1 ----------------+----------+--------------------+-------------------+---------- x.. x..6o.. ♦ 12 0 0 | 6 12 0 0 0 0 0 | 6 2 0 0 0 0 0 0 | 1 * * * * ... xx.6oo.&#x ♦ 6 6 0 | 0 6 6 6 0 0 0 | 0 1 6 0 1 0 0 0 | * 2 * * * xux xxx ...&#xt ♦ 4 4 4 | 2 2 4 2 4 2 2 | 1 0 2 2 0 2 1 0 | * * 6 * * ... .xx6.oo&#x ♦ 0 6 6 | 0 0 0 6 6 0 6 | 0 0 0 0 1 6 0 1 | * * * 2 * ..x ..x6..o ♦ 0 0 12 | 0 0 0 0 0 6 12 | 0 0 0 0 0 0 6 2 | * * * * 1
or o.. o..6o.. & | 24 * | 1 2 1 0 | 2 1 2 1 0 | 1 1 2 .o. .o.6.o. | * 12 | 0 0 2 2 | 0 0 4 1 1 | 0 2 2 -------------------+-------+-------------+-------------+------ x.. ... ... & | 2 0 | 12 * * * | 2 0 0 1 0 | 1 0 2 ... x.. ... & | 2 0 | * 24 * * | 1 1 1 0 0 | 1 1 1 oo. oo.6oo.&#x & | 1 1 | * * 24 * | 0 0 2 1 0 | 0 1 2 ... .x. ... | 0 2 | * * * 12 | 0 0 2 0 1 | 0 2 1 -------------------+-------+-------------+-------------+------ x.. x.. ... & | 4 0 | 2 2 0 0 | 12 * * * * | 1 0 1 ... x..6o.. & | 6 0 | 0 6 0 0 | * 4 * * * | 1 1 0 ... xx. ...&#x & | 2 2 | 0 1 2 1 | * * 24 * * | 0 1 1 xux ... ...&#xt | 4 2 | 2 0 4 0 | * * * 6 * | 0 0 2 ... .x.6.o. | 0 6 | 0 0 0 6 | * * * * 2 | 0 2 0 -------------------+-------+-------------+-------------+------ x.. x..6o.. & ♦ 12 0 | 6 12 0 0 | 6 2 0 0 0 | 2 * * ... xx.6oo.&#x & ♦ 6 6 | 0 6 6 6 | 0 1 6 0 1 | * 4 * xux xxx ...&#xt ♦ 8 4 | 4 4 8 2 | 2 0 4 2 0 | * * 6
xux xxx3xxx&#xt → both heights = sqrt(3)/2 = 0.866025 (hip || pseudo (x,u)-hip || hip) o.. o..3o.. | 12 * * | 1 1 1 1 0 0 0 0 0 0 | 1 1 1 1 1 1 0 0 0 0 0 0 | 1 1 1 1 0 0 .o. .o.3.o. | * 12 * | 0 0 0 1 1 1 1 0 0 0 | 0 0 0 1 1 1 1 1 1 0 0 0 | 0 1 1 1 1 0 ..o ..o3..o | * * 12 | 0 0 0 0 0 0 1 1 1 1 | 0 0 0 1 0 0 0 1 1 1 1 1 | 0 1 1 0 1 1 ----------------+----------+-----------------------+-------------------------+------------ x.. ... ... | 2 0 0 | 6 * * * * * * * * * | 1 1 0 1 0 0 0 0 0 0 0 0 | 1 1 1 0 0 0 ... x.. ... | 2 0 0 | * 6 * * * * * * * * | 1 0 1 0 1 0 0 0 0 0 0 0 | 1 1 0 1 0 0 ... ... x.. | 2 0 0 | * * 6 * * * * * * * | 0 1 1 0 0 1 0 0 0 0 0 0 | 1 0 1 1 0 0 oo. oo.3oo.&#x | 1 1 0 | * * * 12 * * * * * * | 0 0 0 1 1 1 0 0 0 0 0 0 | 0 1 1 1 0 0 ... .x. ... | 0 2 0 | * * * * 6 * * * * * | 0 0 0 0 1 0 1 1 0 0 0 0 | 0 1 0 1 1 0 ... ... .x. | 0 2 0 | * * * * * 6 * * * * | 0 0 0 0 0 1 1 0 1 0 0 0 | 0 0 1 1 1 0 .oo .oo3.oo&#x | 0 1 1 | * * * * * * 12 * * * | 0 0 0 1 0 0 0 1 1 0 0 0 | 0 1 1 0 1 0 ..x ... ... | 0 0 2 | * * * * * * * 6 * * | 0 0 0 1 0 0 0 0 0 1 1 0 | 0 1 1 0 0 1 ... ..x ... | 0 0 2 | * * * * * * * * 6 * | 0 0 0 0 0 0 0 1 0 1 0 1 | 0 1 0 0 1 1 ... ... ..x | 0 0 2 | * * * * * * * * * 6 | 0 0 0 0 0 0 0 0 1 0 1 1 | 0 0 1 0 1 1 ----------------+----------+-----------------------+-------------------------+------------ x.. x.. ... | 4 0 0 | 2 2 0 0 0 0 0 0 0 0 | 3 * * * * * * * * * * * | 1 1 0 0 0 0 x.. ... x.. | 4 0 0 | 2 0 2 0 0 0 0 0 0 0 | * 3 * * * * * * * * * * | 1 0 1 0 0 0 ... x..3x.. | 6 0 0 | 0 3 3 0 0 0 0 0 0 0 | * * 2 * * * * * * * * * | 1 0 0 1 0 0 xux ... ...&#xt | 2 2 2 | 1 0 0 2 0 0 2 1 0 0 | * * * 6 * * * * * * * * | 0 1 1 0 0 0 ... xx. ...&#x | 2 2 0 | 0 1 0 2 1 0 0 0 0 0 | * * * * 6 * * * * * * * | 0 1 0 1 0 0 ... ... xx.&#x | 2 2 0 | 0 0 1 2 0 1 0 0 0 0 | * * * * * 6 * * * * * * | 0 0 1 1 0 0 ... .x.3.x. | 0 6 0 | 0 0 0 0 3 3 0 0 0 0 | * * * * * * 2 * * * * * | 0 0 0 1 1 0 ... .xx ...&#x | 0 2 2 | 0 0 0 0 1 0 2 0 1 0 | * * * * * * * 6 * * * * | 0 1 0 0 1 0 ... ... .xx&#x | 0 2 2 | 0 0 0 0 0 1 2 0 0 1 | * * * * * * * * 6 * * * | 0 0 1 0 1 0 ..x ..x ... | 0 0 4 | 0 0 0 0 0 0 0 2 2 0 | * * * * * * * * * 3 * * | 0 1 0 0 0 1 ..x ... ..x | 0 0 4 | 0 0 0 0 0 0 0 2 0 2 | * * * * * * * * * * 3 * | 0 0 1 0 0 1 ... ..x3..x | 0 0 6 | 0 0 0 0 0 0 0 0 3 3 | * * * * * * * * * * * 2 | 0 0 0 0 1 1 ----------------+----------+-----------------------+-------------------------+------------ x.. x..3x.. ♦ 12 0 0 | 6 6 6 0 0 0 0 0 0 0 | 3 3 2 0 0 0 0 0 0 0 0 0 | 1 * * * * * xux xxx ...&#xt ♦ 4 4 4 | 2 2 0 4 2 0 4 2 2 0 | 1 0 0 2 2 0 0 2 0 1 0 0 | * 3 * * * * xux ... xxx&#xt ♦ 4 4 4 | 2 0 2 4 0 2 4 2 0 2 | 0 1 0 2 0 2 0 0 2 0 1 0 | * * 3 * * * ... xx.3xx.&#x ♦ 6 6 0 | 0 3 3 6 3 3 0 0 0 0 | 0 0 1 0 3 3 1 0 0 0 0 0 | * * * 2 * * ... .xx3.xx&#x ♦ 0 6 6 | 0 0 0 0 3 3 6 0 3 3 | 0 0 0 0 0 0 1 3 3 0 0 1 | * * * * 2 * ..x ..x3..x ♦ 0 0 12 | 0 0 0 0 0 0 0 6 6 6 | 0 0 0 0 0 0 0 0 0 3 3 2 | * * * * * 1
© 2004-2026 | top of page |