Ridge-facetings of the great dirhombicosidodecahedron ship   (part 1)

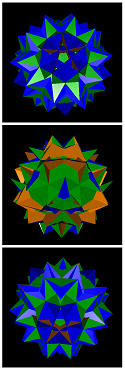
Possible facets here are the 24 pentagrams, 40 triangles, and 60 squares of the comodore itself together with 120 more internal triangles. The general naming code here is accordingly gidrid-#{5/2}-#{3}-#{4}. This gives rise for exactly 406 (pure polyhedral) edge-facetings with n-gonal axial rotation symmetries, provided n = 5 (plus uncounted compounds). In fact, 1 polyhedral ones has full icosahedral symmetry, 1 polyhedral ones has chiral icosahedral symmetry, 10 have 5-fold pyramidal symmetry, 250 have 5-fold chiral pyramidal symmetry, 15 have 5-fold antiprismatic symmetry, 9 have 5-fold chiral antiprismatic symmetry (i.e. anti-aligned orientations of base margins), 120 have 5-fold rotational glyde reflection symmetry (i.e. aligned orientations of base margins) 1 has octahedral symmetry, 1 has tetrahedral symmetry. And a total of 117 800 ridge-facetings have some 3-fold symmetry. Only the highest symmetrical compounds, the icosahedral symmetric dasi (compound of 20 octs) and the chiral icosahedral symmetric sapisseri (compound of 20 thahs), are being displayed additionally.

Due to its amount this page is being split into parts. The following parts are available:

1. part (this page) : full icosahedral, chiral icosahedral, 5-fold pyramidal, and 5-fold antiprismatic symmetry
2. part : 5-fold antiprismatic (continued), 5-fold chiral antiprismatic, 5-fold chiral pyramidal, and 5-fold rotational glyde reflection symmetry

The octahedral symmetric case clearly is oct itself and the tetrahedral symmetric one is thah. Those 2 and all other 117 798 cases with 3-fold symmetries, which then again contain all the 24 pentagrams, had only been counted by means of a computer research, cf. the article Axial-Symmetrical Edge-Facetings of Uniform Polyhedra. Neither a picture, nor a VRML, nor its mere code is being provided for obvious reason. – Even for the 2 last large groups of 5-fold symmetries only their VRML file, linked by its respective naming code, is being provided in list form so far.

gidrid-24-40-60 = gidrid	gidrid-0-160-0 = dasi	gidrid-24-80-0 = gisdid	gidrid-0-80-60 = sapisseri	gidrid-24-60-10-v1	gidrid-24-60-10-v2	gidrid-24-60-10-v6	gidrid-24-60-10-v49
icosahedral		chiral icosahedral		5-fold pyramidal ...
gidrid-24-60-10-v50	gidrid-24-60-10-v59	gidrid-24-60-30-v1	gidrid-24-60-30-v13	gidrid-24-80-0-v1	gidrid-24-80-0-v3	gidrid-24-40-20-v1	gidrid-24-40-20-v2
... 5-fold pyramidal						5-fold antiprismatic ...
gidrid-24-40-20-v7	gidrid-24-40-20-v8	gidrid-24-40-20-v11	gidrid-24-40-20-v12	gidrid-24-40-20-v40	gidrid-24-40-20-v41	gidrid-24-40-20-v45	gidrid-24-40-40-v1
... 5-fold antiprismatic ...
continue >>