Acronym	gik vixathi
Name	great skewverted hexacositriakishecatonicosachoro
Cross sections	©
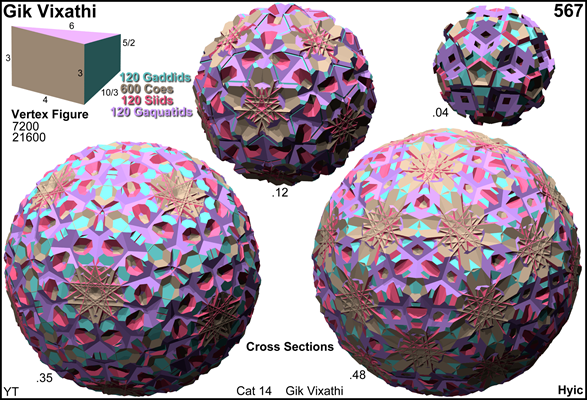Circumradius	sqrt[13-4 sqrt(5)] = 2.013884
Colonel of regiment	(is itself locally convex – uniform polychoral members: by cells: co dip gaddid gaquatid idtid oho qrid sidditdid siid toe gikkiv datapixady 600 720 0 0 0 0 120 120 0 0 gik vixathi 600 0 120 120 0 0 0 0 120 0 gikkiv datixathi 0 0 120 0 120 600 0 120 0 0 gik vadixady 0 0 0 0 0 600 120 0 120 600 & others)
Face vector	7200, 21600, 13680, 960
Confer	general polytopal classes: Wythoffian polychora
External links

As abstract polytope gik vixathi is isomorphic to sik vixathi, thereby replacing pentagrams by pentagons and decagrams by decagons, respectively siid by giid, gaddid by saddid, and gaquatid by grid.

Incidence matrix according to Dynkin symbol

        _o_        
    _3-  |  -3_    
 x<     5/2     >x 
    -3_  |  5/3    
        -x-        

o3x3x5/3x3*a5/2*c

. . .   .         | 7200 |    2    2    2 |    1    1    1    2    2    2 |   1   1   1   2
------------------+------+----------------+-------------------------------+----------------
. x .   .         |    2 | 7200    *    * |    1    0    0    1    1    0 |   1   1   0   1
. . x   .         |    2 |    * 7200    * |    0    1    0    1    0    1 |   1   0   1   1
. . .   x         |    2 |    *    * 7200 |    0    0    1    0    1    1 |   0   1   1   1
------------------+------+----------------+-------------------------------+----------------
o3x .   .         |    3 |    3    0    0 | 2400    *    *    *    *    * |   1   1   0   0
o . x   . *a5/2*c |    5 |    0    5    0 |    * 1440    *    *    *    * |   1   0   1   0
o . .   x3*a      |    3 |    0    0    3 |    *    * 2400    *    *    * |   0   1   1   0
. x3x   .         |    6 |    3    3    0 |    *    *    * 2400    *    * |   1   0   0   1
. x .   x         |    4 |    2    0    2 |    *    *    *    * 3600    * |   0   1   0   1
. . x5/3x         |   10 |    0    5    5 |    *    *    *    *    * 1440 |   0   0   1   1
------------------+------+----------------+-------------------------------+----------------
o3x3x   . *a5/2*c ♦   60 |   60   60    0 |   20   12    0   20    0    0 | 120   *   *   *
o3x .   x3*a      ♦   12 |   12    0   12 |    4    0    4    0    6    0 |   * 600   *   *
o . x5/3x3*a5/2*c ♦   60 |    0   60   60 |    0   12   20    0    0   12 |   *   * 120   *
. x3x5/3x         ♦  120 |   60   60   60 |    0    0    0   20   30   12 |   *   *   * 120

        _o_        
    3/2  |  3/2    
 x<     5/3     >x 
    -3_  |  5/3    
        -x-        

o3/2x3x5/3x3/2*a5/3*c

.   . .   .           | 7200 |    2    2    2 |    1    1    1    2    2    2 |   1   1   1   2
----------------------+------+----------------+-------------------------------+----------------
.   x .   .           |    2 | 7200    *    * |    1    0    0    1    1    0 |   1   1   0   1
.   . x   .           |    2 |    * 7200    * |    0    1    0    1    0    1 |   1   0   1   1
.   . .   x           |    2 |    *    * 7200 |    0    0    1    0    1    1 |   0   1   1   1
----------------------+------+----------------+-------------------------------+----------------
o3/2x .   .           |    3 |    3    0    0 | 2400    *    *    *    *    * |   1   1   0   0
o   . x   .   *a5/3*c |    5 |    0    5    0 |    * 1440    *    *    *    * |   1   0   1   0
o   . .   x3/2*a      |    3 |    0    0    3 |    *    * 2400    *    *    * |   0   1   1   0
.   x3x   .           |    6 |    3    3    0 |    *    *    * 2400    *    * |   1   0   0   1
.   x .   x           |    4 |    2    0    2 |    *    *    *    * 3600    * |   0   1   0   1
.   . x5/3x           |   10 |    0    5    5 |    *    *    *    *    * 1440 |   0   0   1   1
----------------------+------+----------------+-------------------------------+----------------
o3/2x3x   .   *a5/3*c ♦   60 |   60   60    0 |   20   12    0   20    0    0 | 120   *   *   *
o3/2x .   x3/2*a      ♦   12 |   12    0   12 |    4    0    4    0    6    0 |   * 600   *   *
o   . x5/3x3/2*a5/3*c ♦   60 |    0   60   60 |    0   12   20    0    0   12 |   *   * 120   *
.   x3x5/3x           ♦  120 |   60   60   60 |    0    0    0   20   30   12 |   *   *   * 120