Acronym	bipgy srit
Name	bipara(bi)gyrated small rhombitesseract, pseudo cantellated tesseract
	© ©
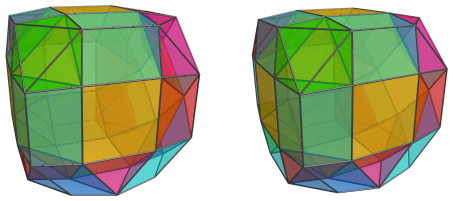Circumradius	sqrt[2+sqrt(2)] = 1.847759
Dihedral angles	at {4} between squippy and trip:   arccos(-sqrt[(3+2 sqrt(2))/6]) = 170.264390° at {4} between trip and trip:   arccos[-sqrt(8)/3] = 160.528779° at {3} between oct and trip:   150° at {3} between squippy and trip:   150° at {4} between esquigybcu and squippy:   135° at {4} between esquigybcu and trip:   arccos[-1/sqrt(3)] = 125.264390° at {3} between esquigybcu and oct:   120° at {3} between esquigybcu and squippy:   120° at {4} between esquigybcu and esquigybcu:   90°
Pattern (parts of total size: 8x8 squares)	A---7---A---8---H---9---H---8---A-... | \ : / | | \ : / | | 1==B,E==1=======4===F===4=======1= (EF.. remains) | / : \ | | / : \ | | A---7---A---8---H---9---H---8---A-... | : | | \ : / | | 2 : 2 5 D 5 2 | : | | / : \ | | H---a---H---b---I---c---I---b---H-... | \ : / | \ / | : | \ / | 3===C===3===G===6===:===6===G===3= (GG.. gyrated) | / : \ | / \ | : | / \ | H---a---H---b---I---c---I---b---H-... | : | | \ : / | | 2 : 2 5 D 5 2 | : | | / : \ | | A---7---A---8---H---9---H---8---A-... | \ : / | | \ : / | | (BC.. (DD.. (etc.) remains) gyrated)
Face vector	96, 288, 260, 68
Confer	uniform relative: srit   odip   segmentochora: {4} || op   related CRFs: cyted srit   cyte gysrit   bicyte gysrit
External links

The symmetry of srit will be broken by an inscribed odip. Here the squares of odip are used for separation: in both of these halves an opposite pair of {4} || op would remain intact, while the other one each will be gyrated. – As can be seen from the above pattern, the relative choice, even if starting by an appropriate augmentation of odip, is irrelevant, they just would come out in different orientations of the same figure. – All octs, but the ones marked in the pattern by "B,E", thereby will be halved into squippy).

This polychoron alternatively can be obtained by augmenting alternate ops of both rings of ops within odip by {4} || op. Then the opposite ones in each ring have to use the same orientations, while the orthogonal pair, has to be relatively gyrated.

This alternate gyration is what produces esquigybcu (= J37) instead of the sirco used for srit. Those J37 cells, also being called pseudo rhombicuboctahedra, gave rise for the analogue (alternate) naming of pseudo cantellated tesseract, here.

Incidence matrix

16  *  * * *  * |  2  2  0  0  0  0  2  0  0  0  0 0 0 |  2  1 0  0 0  2  2  0  0  0  0  0  2  0  0 0 0 | 1 0  0  2 0 0 2  (A)
 * 32  * * *  * |  0  1  1  1  1  0  0  1  1  0  0 0 0 |  1  1 1  1 0  0  0  1  1  1  1  0  1  1  0 0 0 | 0 1  1  1 1 0 2  (H)
 *  * 16 * *  * |  0  0  0  0  2  2  0  0  0  2  0 0 0 |  0  1 0  2 1  0  0  0  0  0  2  2  0  0  2 0 0 | 0 0  2  0 0 2 2  (I)
 *  *  * 8 *  * |  0  0  0  0  0  0  4  0  0  0  2 0 0 |  0  0 0  0 0  2  2  0  0  0  0  0  4  0  0 1 0 | 1 0  0  2 0 0 2  (B,E)
 *  *  * * 8  * |  0  0  0  0  0  0  0  4  0  0  2 0 0 |  0  0 0  0 0  0  0  2  2  0  0  0  4  0  0 1 0 | 0 1  0  2 0 0 2  (C,F)
 *  *  * * * 16 |  0  0  0  0  0  0  0  0  2  2  0 1 1 |  0  0 0  0 0  0  0  0  0  1  2  1  0  2  2 0 1 | 0 0  1  0 1 1 2  (D,G)
----------------+--------------------------------------+------------------------------------------------+----------------
 2  0  0 0 0  0 | 16  *  *  *  *  *  *  *  *  *  * * * |  1  0 0  0 0  1  1  0  0  0  0  0  0  0  0 0 0 | 1 0  0  1 0 0 1  (1,7)
 1  1  0 0 0  0 |  * 32  *  *  *  *  *  *  *  *  * * * |  1  1 0  0 0  0  0  0  0  0  0  0  1  0  0 0 0 | 0 0  0  1 0 0 2  (2,8)
 0  2  0 0 0  0 |  *  * 16  *  *  *  *  *  *  *  * * * |  0  0 1  1 0  0  0  1  0  1  0  0  0  0  0 0 0 | 0 1  1  0 1 0 1  (3,9)
 0  2  0 0 0  0 |  *  *  * 16  *  *  *  *  *  *  * * * |  1  0 1  0 0  0  0  0  1  0  0  0  0  1  0 0 0 | 0 1  0  1 1 0 1  (4,a)
 0  1  1 0 0  0 |  *  *  *  * 32  *  *  *  *  *  * * * |  0  1 0  1 0  0  0  0  0  0  1  0  0  0  0 0 0 | 0 0  1  0 0 0 2  (5,b)
 0  0  2 0 0  0 |  *  *  *  *  * 16  *  *  *  *  * * * |  0  0 0  1 1  0  0  0  0  0  0  1  0  0  1 0 0 | 0 0  1  0 0 2 1  (6,c)
 1  0  0 1 0  0 |  *  *  *  *  *  * 32  *  *  *  * * * |  0  0 0  0 0  1  1  0  0  0  0  0  1  0  0 0 0 | 1 0  0  1 0 0 1
 0  1  0 0 1  0 |  *  *  *  *  *  *  * 32  *  *  * * * |  0  0 0  0 0  0  0  1  1  0  0  0  1  0  0 0 0 | 0 1  0  1 0 0 1
 0  1  0 0 0  1 |  *  *  *  *  *  *  *  * 32  *  * * * |  0  0 0  0 0  0  0  0  0  1  1  0  0  1  0 0 0 | 0 0  1  0 1 0 1
 0  0  1 0 0  1 |  *  *  *  *  *  *  *  *  * 32  * * * |  0  0 0  0 0  0  0  0  0  0  1  1  0  0  1 0 0 | 0 0  1  0 0 1 1
 0  0  0 1 1  0 |  *  *  *  *  *  *  *  *  *  * 16 * * |  0  0 0  0 0  0  0  0  0  0  0  0  2  0  0 1 0 | 0 0  0  1 0 0 2
 0  0  0 0 0  2 |  *  *  *  *  *  *  *  *  *  *  * 8 * |  0  0 0  0 0  0  0  0  0  0  0  0  0  2  0 0 1 | 0 0  0  0 1 0 2
 0  0  0 0 0  2 |  *  *  *  *  *  *  *  *  *  *  * * 8 |  0  0 0  0 0  0  0  0  0  0  0  0  0  0  2 0 1 | 0 0  0  0 0 1 2
----------------+--------------------------------------+------------------------------------------------+----------------
 2  2  0 0 0  0 |  1  2  0  1  0  0  0  0  0  0  0 0 0 | 16  * *  * *  *  *  *  *  *  *  *  *  *  * * * | 0 0  0  1 0 0 1
 1  2  1 0 0  0 |  0  2  0  0  2  0  0  0  0  0  0 0 0 |  * 16 *  * *  *  *  *  *  *  *  *  *  *  * * * | 0 0  0  0 0 0 2
 0  4  0 0 0  0 |  0  0  2  2  0  0  0  0  0  0  0 0 0 |  *  * 8  * *  *  *  *  *  *  *  *  *  *  * * * | 0 1  0  0 1 0 0
 0  2  2 0 0  0 |  0  0  1  0  2  1  0  0  0  0  0 0 0 |  *  * * 16 *  *  *  *  *  *  *  *  *  *  * * * | 0 0  1  0 0 0 1
 0  0  4 0 0  0 |  0  0  0  0  0  4  0  0  0  0  0 0 0 |  *  * *  * 4  *  *  *  *  *  *  *  *  *  * * * | 0 0  0  0 0 2 0
 2  0  0 1 0  0 |  1  0  0  0  0  0  2  0  0  0  0 0 0 |  *  * *  * * 16  *  *  *  *  *  *  *  *  * * * | 1 0  0  1 0 0 0
 2  0  0 1 0  0 |  1  0  0  0  0  0  2  0  0  0  0 0 0 |  *  * *  * *  * 16  *  *  *  *  *  *  *  * * * | 1 0  0  0 0 0 1
 0  2  0 0 1  0 |  0  0  1  0  0  0  0  2  0  0  0 0 0 |  *  * *  * *  *  * 16  *  *  *  *  *  *  * * * | 0 1  0  0 0 0 1
 0  2  0 0 1  0 |  0  0  0  1  0  0  0  2  0  0  0 0 0 |  *  * *  * *  *  *  * 16  *  *  *  *  *  * * * | 0 1  0  1 0 0 0
 0  2  0 0 0  1 |  0  0  1  0  0  0  0  0  2  0  0 0 0 |  *  * *  * *  *  *  *  * 16  *  *  *  *  * * * | 0 0  1  0 1 0 0
 0  1  1 0 0  1 |  0  0  0  0  1  0  0  0  1  1  0 0 0 |  *  * *  * *  *  *  *  *  * 32  *  *  *  * * * | 0 0  1  0 0 0 1
 0  0  2 0 0  1 |  0  0  0  0  0  1  0  0  0  2  0 0 0 |  *  * *  * *  *  *  *  *  *  * 16  *  *  * * * | 0 0  1  0 0 1 0
 1  1  0 1 1  0 |  0  1  0  0  0  0  1  1  0  0  1 0 0 |  *  * *  * *  *  *  *  *  *  *  * 32  *  * * * | 0 0  0  1 0 0 1
 0  2  0 0 0  2 |  0  0  0  1  0  0  0  0  2  0  0 1 0 |  *  * *  * *  *  *  *  *  *  *  *  * 16  * * * | 0 0  0  0 1 0 1
 0  0  2 0 0  2 |  0  0  0  0  0  1  0  0  0  2  0 0 1 |  *  * *  * *  *  *  *  *  *  *  *  *  * 16 * * | 0 0  0  0 0 1 1
 0  0  0 2 2  0 |  0  0  0  0  0  0  0  0  0  0  4 0 0 |  *  * *  * *  *  *  *  *  *  *  *  *  *  * 4 * | 0 0  0  0 0 0 2
 0  0  0 0 0  4 |  0  0  0  0  0  0  0  0  0  0  0 2 2 |  *  * *  * *  *  *  *  *  *  *  *  *  *  * * 4 | 0 0  0  0 0 0 2
----------------+--------------------------------------+------------------------------------------------+----------------
 4  0  0 2 0  0 |  4  0  0  0  0  0  8  0  0  0  0 0 0 |  0  0 0  0 0  4  4  0  0  0  0  0  0  0  0 0 0 | 4 *  *  * * * *  oct
 0  4  0 0 1  0 |  0  0  2  2  0  0  0  4  0  0  0 0 0 |  0  0 1  0 0  0  0  2  2  0  0  0  0  0  0 0 0 | * 8  *  * * * *  squippy (J1)
 0  2  2 0 0  1 |  0  0  1  0  2  1  0  0  2  2  0 0 0 |  0  0 0  1 0  0  0  0  0  1  2  1  0  0  0 0 0 | * * 16  * * * *  squippy (J1)
 2  2  0 1 1  0 |  1  2  0  1  0  0  2  2  0  0  1 0 0 |  1  0 0  0 0  1  0  0  1  0  0  0  2  0  0 0 0 | * *  * 16 * * *  trip
 0  4  0 0 0  2 |  0  0  2  2  0  0  0  0  4  0  0 1 0 |  0  0 1  0 0  0  0  0  0  2  0  0  0  2  0 0 0 | * *  *  * 8 * *  trip
 0  0  4 0 0  2 |  0  0  0  0  0  4  0  0  0  4  0 0 1 |  0  0 0  0 1  0  0  0  0  0  0  2  0  0  2 0 0 | * *  *  * * 8 *  trip
 4  8  4 2 2  4 |  2  8  2  2  8  2  4  4  4  4  4 2 2 |  2  4 0  2 0  0  2  2  0  0  4  0  4  2  2 1 1 | * *  *  * * * 8  esquigybcu (J37)