Acronym	gacid
Name	great complex icosidodecahedron
Circumradius	sqrt[(5-sqrt(5))/8] = 0.587785
Vertex figure	[(5/3,3)5] (type A) or [(5/2,3)5]/3 (type B)
General of army	ike
Colonel of regiment	sissid
Confer	non-Grünbaumian masters: gike   sissid   Grünbaumian relatives: sissid+2gike   2sissid+gike   sissid+3gike   3sissid+gike   2sissid+4gike   4sissid+2gike   general polytopal classes: Wythoffian polyhedra
External links

As abstract polytope gacid is isomorphic to cid, thereby replacing pentagrams by pentagons.

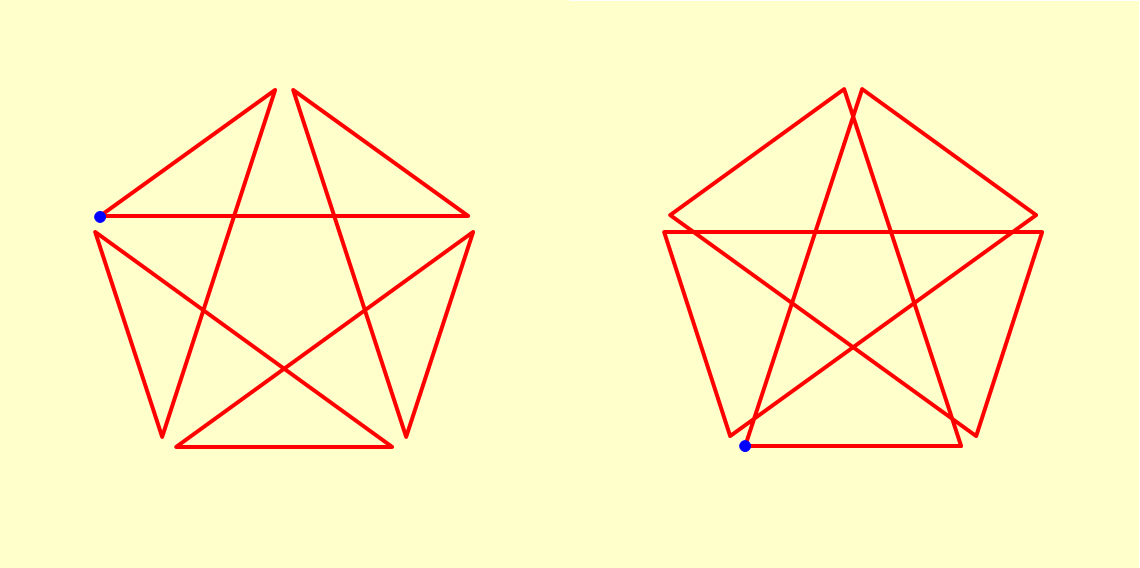
Looks like a compound of the great icosahedron (gike) and the small stellated dodecahedron (sissid), and indeed edges coincide by pairs, but vertices are identified. Note that without edge-doubling this would be a tetradic figure (type C).

Incidence matrix according to Dynkin symbol

o5/3x3o5*a (type A)

.   . . | 12 | 10 |  5  5
--------+----+----+------
.   x . |  2 | 60 |  1  1
--------+----+----+------
o5/3x . |  5 |  5 | 12  *
.   x3o |  3 |  3 |  * 20

o3/2x5/2o5*a (type A)

.   .   . | 12 | 10 |  5  5
----------+----+----+------
.   x   . |  2 | 60 |  1  1
----------+----+----+------
o3/2x   . |  3 |  3 | 20  *
.   x5/2o |  5 |  5 |  * 12

x5/3o5/2o3*a (type B)

.   .   .    | 12 | 10 |  5  5
-------------+----+----+------
x   .   .    |  2 | 60 |  1  1
-------------+----+----+------
x5/3o   .    |  5 |  5 | 12  *
x   .   o3*a |  3 |  3 |  * 20

o5/3o5/2x3*a (type B)

.   .   .    | 12 | 10 |  5  5
-------------+----+----+------
.   .   x    |  2 | 60 |  1  1
-------------+----+----+------
.   o5/2x    |  5 |  5 | 12  *
o   .   x3*a |  3 |  3 |  * 20

x3/2o5/2o5/2*a (type B)

.   .   .      | 12 | 10 |  5  5
---------------+----+----+------
x   .   .      |  2 | 60 |  1  1
---------------+----+----+------
x3/2o   .      |  3 |  3 | 20  *
x   .   o5/2*a |  5 |  5 |  * 12

o5/4o5/2x3*a (type A)

.   .   .    | 12 | 10 |  5  5
-------------+----+----+------
.   .   x    |  2 | 60 |  1  1
-------------+----+----+------
.   o5/2x    |  5 |  5 | 12  *
o   .   x3*a |  3 |  3 |  * 20

x3/2o5/3o5/3*a (type B)

.   .   .      | 12 | 10 |  5  5
---------------+----+----+------
x   .   .      |  2 | 60 |  1  1
---------------+----+----+------
x3/2o   .      |  3 |  3 | 20  *
x   .   o5/3*a |  5 |  5 |  * 12

o5/4o3/2x5/3*a (type A)

.   .   .      | 12 | 10 |  5  5
---------------+----+----+------
.   .   x      |  2 | 60 |  1  1
---------------+----+----+------
.   o3/2x      |  3 |  3 | 20  *
o   .   x5/3*a |  5 |  5 |  * 12

(Type C)

12 |  5 |  5  5
---+----+------
 2 | 30 |  2  2  :4 incident faces
---+----+------
 3 |  3 | 20  *
 5 |  5 |  * 12  :pentagrams

β3o5/2o (type A)

both( . .   . ) | 12 | 10 |  5  5
----------------+----+----+------
sefa( β3o   . ) |  2 | 60 |  1  1
----------------+----+----+------
      β3o   .   ♦  3 |  3 | 20  *
sefa( β3o5/2o ) |  5 |  5 |  * 12

starting figure: x3o5/2o

as uniform compound

  12 |  5  5 |  5  5 || 1 1
-----+-------+-------++----
   2 | 30  * |  2  0 || 1 0
   2 |  * 30 |  0  2 || 0 1
-----+-------+-------++----
   3 |  3  0 | 20  * || 1 0
   5 |  0  5 |  * 12 || 0 1
-----+-------+-------++----
♦ 12 | 30  0 | 20  0 || 1 *
♦ 12 |  0 30 |  0 20 || * 1