Would multi-snubbing be allowable in general?

Consider the following formal notation for alternated facetings: let P be some polytope and p be some set of subelements, which is meant to be alternated, then call the resulting snub Q = AF(P,p). In several occasions then this procedure can be applied iteratedly, that is, that Q might have in turn a set of subelements q, which could be alternated. That is, we consider here R = AF(Q,q) = AF(AF(P,p),q). – As such there is no harm here soever. The sequencing is readily been seen from this notation.

Quite different this same theme becomes when being applied to Wythoffian starting figures, and the application of alternated facetings will be given by Stott node markings. Let's use s for one of the operations and s' for the other. Without some clear advice for sequencing (e.g. like indexings), the result would become ambiguous in general! – Or turned differently: Such a multi-snubbed notation would be allowable only, if either sequencing would result in the same outcome.

A proof for generally different outcomes could be given by a simple example:

Consider sPs2Qs' in either sequencing. It will be proven, that this symbol will not be allowable. What would be obvious from that symbol however, is the starting figure, which here ought to be xPx2Qx. The subelements of that starting polyhedron or tiling obviously are xPx . (2P-gons), x . x (squares), and . x2Qx (4Q-gons).

s before s'

The first step then would be to derive sPs2Qx. In here the to be alternated elements would be the alternate edges of the 2Q-gons, i.e. . . x. Thereby the 2P-gons get alternated in their vertices, thus resulting in P-gons (with equal, but different edge size). The 4Q-gons then become 2Q-gons (with alternate edge size). And the squares would reduce to one of their sides. As sefas (sectioning facets occuring underneath the to be alternated former elements) here occure new tetragons (trapezes). These trapezes will have the new 2Q-gons at their opposite, parallel edges, while the new P-gons are incident at their opposite lacing edges. Note we have 3 edge sizes (without relaxation), where the 2Q-gon has alternating 2 of them, while the P-gon uses throughout the 3rd. The resulting vertex figure here would be [P,4,2Q,4].
Thus sPs2Qx turns out to be equivalent to xPo2Qx (after relaxation).

In the second step we thus would have to consider sPs2Qs' = xPo2Qs' here. The to be alternated elements this time are the P-gons. Half of them would be rejected, half would remain as is. The 2Q-gons then get reduced to mere regular Q-gons. The just derived squares x . x of the new starting figure (i.e. those trapezes of the former derivation process) again get reduced to one of their sides. As sefas new 2P-gons re-occure again. Thus the resulting vertex figure here becomes [P,2P,Q,2P].
Accordingly (in this sequencing) we get sPs2Qs' = xPxPoQ*a (after relaxation).

s' before s

Here we would have to consider xPx2Qs' first. I.e. we will have to alternate the 2P-gons (xPx .) here. The rejected ones then would get replaced by larger 2P-gons (as sefas) here. The 4Q-gons again get reduced to 2Q-gons (of alternating edge size). And the squares again get reduced to one of their sides. The resulting vertex figure here would be [2P,2Q,2Q].
Thus xPx2Qs' turns out to be equivalent to xPx2Qo (after relaxation).

In the second step we thus would have to consider sPs2Qs' = sPs2Qo here. That is, we would have to alternate the vertices (. . o) now. Then the 2P-gons clearly become regular P-gons and the 2Q-gons become mere regular Q-gons (of different edge size, when considered without relaxation – assuming P ≠ Q). The additional face (the sefa) here is the former vertex figure, i.e. an isocele triangle. Relaxation thus results in some tiling with verf [P,3,P,3,Q,3].
I.e. (in this sequencing) we get sPs2Qs' = sPsPsQ*a.

Finally we will just provide some specific cases out of these derived examplifying class:
E.g. s3s4s' (case P=3, Q=2):   x3x3o2*a = x3x3o (tut)   vs.   s3s3s2*a = s3s3s (= x3o5o, ike).

s before s'
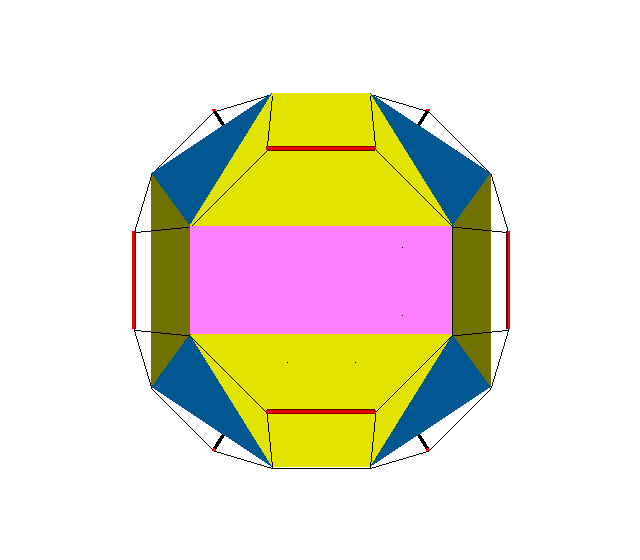
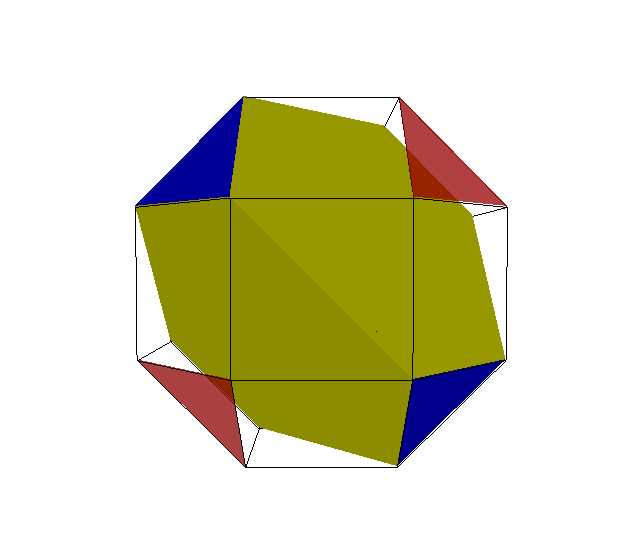
x3x4x → s3s4x ≈ x3o4x	x3o4x → x3o4s' ≈ x3x3o
s after s'
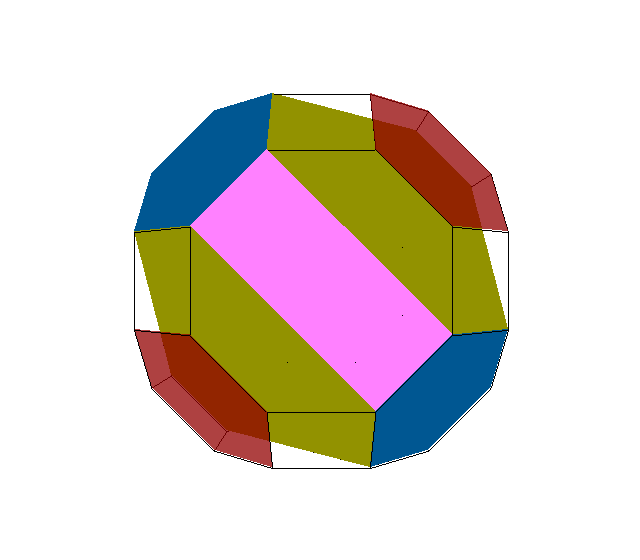
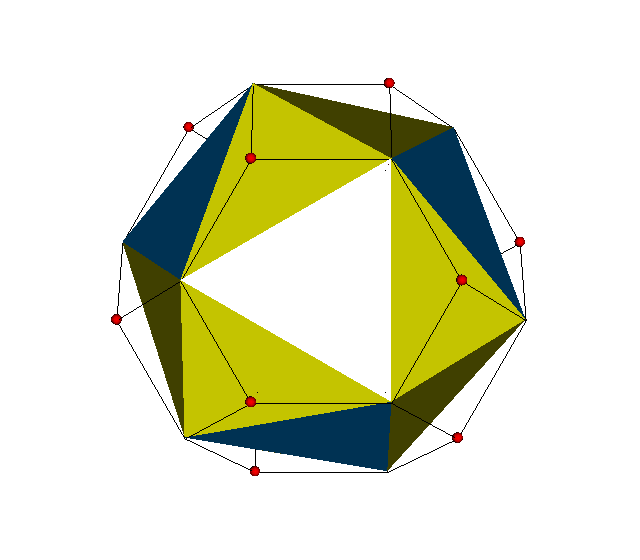
x3x4x → x3x4s' ≈ x3x4o	x3x4o → s3s4o ≈ x3o5o

Likewise s3s6s' (case P=3, Q=3):   x3x3o3*a (= o3x6o, that)   vs.   s3s3s3*a (= x3o6o, trat).

Thus, providing such multi-snub symbols (without sequencing advice) is allowable only, when either outcome will result in the same object.

A small compilation of such allowable multi-snubbings however would include e.g.:

s4o4s' (snasquat)
s4x4s' (squat)

s3s4s'3s' (prissi)
s3s4o4s'  (hyperbolic x4s4o *b3s tesselation)
s4o3o4s'  (batatoh)
s4o3o6s'  (quishexah)

s4o3o3o4s' (rittit)