⭳







the corresponding VRML preview in this canvas
= defbideb
= sifdodeb
= sifdadedo
= cube
= quistet

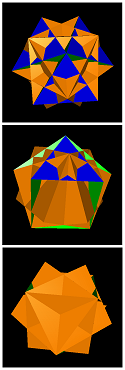


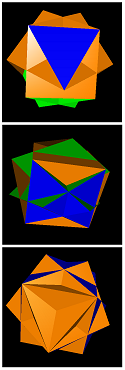

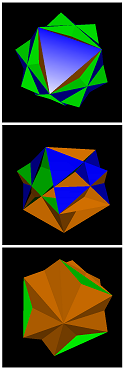

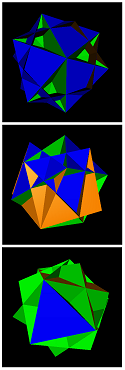
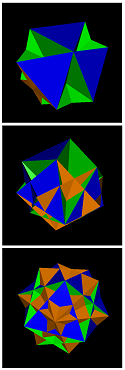
= trippescu
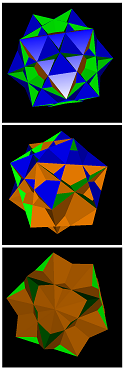









(comp. †)
= dritit
| Site Map | Polytopes | Dynkin Diagrams | Vertex Figures, etc. | Incidence Matrices | Index |
Possible facets here are the 12 pentagrams and 20 triangles of the comodore itself together with the 30 internal squares and 12 internal pentagons. The general naming code here is accordingly sidtid-#{5/2}-#{3}-#{4}-#{5}. This gives rise for exactly 161 (pure polyhedral) edge-facetings with n-gonal axial rotation symmetries, provided n > 2 (plus uncounted compounds). In fact, 3 polyhedral ones have full icosahedral symmetry, 46 have 5-fold pyramidal symmetry, 7 have 5-fold antiprismatic symmetry, 1 has cubical symmetry, 1 has chiral tetrahedral symmetry, 76 have 3-fold (full) pyramidal symmetry, 15 have 3-fold chiral pyramidal symmetry, 6 have 3-fold (full) antiprismatic symmetry, and 6 have 3-fold chiral antiprismatic symmetry. Only the full symmetrical compound rhom is being displayed additionally, as this one shows clearly the origin of the possible square facets.
Due to its amount this page is being split into parts. The following parts are available:
| << continue | |||||||||
|

|

|

|

|

|

|

| ||
|
clicking the triple-pictures of the table provides the corresponding VRML preview in this canvas |
sidtid-2-20-10-2 = defbideb |
sidtid-10-0-10-2 = sifdodeb |
sidtid-10-10-10-0 = sifdadedo |
sidtid-0-0-6-0 = cube |
sidtid-0-8-12-0-b = quistet | sidtid-0-2-12-6-a | sidtid-0-2-18-6-a | ||
| ... 5-fold antiprismatic | cubic | tetrahedr.-chiral | 3-fold pyramidal ... | ||||||

|

|

|

|

|

|

|

|

|

|
|
sidtid-0-3-3-3 = trippescu | sidtid-0-3-15-3 | sidtid-0-5-15-9 | sidtid-0-7-9-3-a | sidtid-0-7-9-3-c | sidtid-0-7-9-3-d | sidtid-0-7-9-3-g | sidtid-0-10-6-6-a | sidtid-0-10-6-6-b | sidtid-0-10-6-6-c |
| ... 3-fold pyramidal ... | |||||||||

|

|

|

|

|

|

|

|

|

|
|
sidtid-0-10-12-6 (comp. †) | sidtid-0-12-12-0-a | sidtid-0-12-18-0-a | sidtid-0-15-15-3 | sidtid-0-17-3-9 | sidtid-3-0-6-3-a |
sidtid-3-0-6-3-b = dritit | sidtid-3-0-12-3-a | sidtid-3-0-12-3-b | sidtid-3-2-12-3-a |
| ... 3-fold pyramidal ... | |||||||||
| continue >> | |||||||||
†: sidtid-0-10-12-6 = sidtid-0-3-3-3 (trippescu) + sidtid-0-7-9-3-g, i.e. it happens to be a compound.
© 2004-2026 | top of page |