|
Acronym
|
...
|
|
Name
|
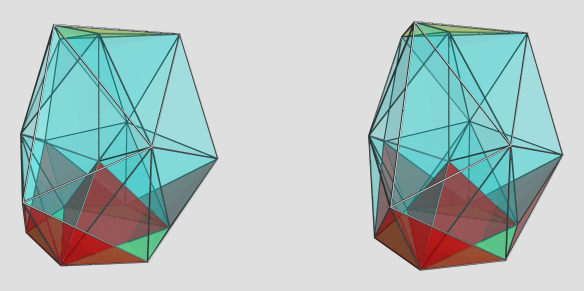
tetra-augmented axially-tetrahedral ursachoron xofo3ooox3oxoo&#xt
|
|
|
 © ©
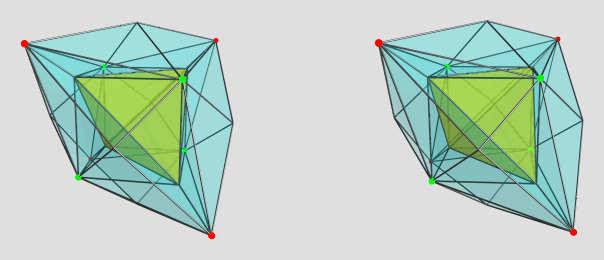 © ©
The second picture shows the bottom x3o3o in yellow, the vertices of the augmentation tips in green (layer o3o3x), and the medial vertices of f3o3o in red.
|
|
Circumradius
|
...
|
Lace city
in approx. ASCII-art
|
o o x x o o
f o o f
o x x o
x o o x
|
+--------------------- x3o3o (tet)
/ +------------- o3o3x (dual tet)
/ / +--------- f3o3o (f-tet)
/ / / +-- o3x3o (oct)
/ / / /
o3o o3o
o3x
x3o x3o
o3o f3o
o3x
|
|
Coordinates
|
-
-
(1/sqrt(2), 0, 0; 1/sqrt(2)) & all permutations in first 3 coord.s & all changes of sign in first 3 coord.s
(layer o3x3o in lace tower description resp. top one in lace city)
-
-
(f/sqrt(8), f/sqrt(8), f/sqrt(8); 1/(F sqrt(8))) & all even permutations in first 3 coord.s & all changes of sign in first 3 coord.s
(layer f3o3o in lace tower description resp. medial one in lace city)
-
-
(1/sqrt(8), 1/sqrt(8), -1/sqrt(8); -(sqrt(5)-2)/sqrt(8)) & all even permutations in first 3 coord.s & all changes of sign in first 3 coord.s
(layer o3o3x in lace tower description resp. the augmentation tips)
-
-
(1/sqrt(8), 1/sqrt(8), 1/sqrt(8); -sqrt(5/8)) & all even permutations in first 3 coord.s & all changes of sign in first 3 coord.s
(layer x3o3o in lace tower description resp. bottom one in lace city)
where f=(1+sqrt(5))/2, F=ff=f+x
|
|
Face vector
|
18, 70, 90, 38
|
|
Confer
|
- related CRFs:
-
tetu
- related segmentochora:
-
teddipy
- uniform relative:
-
hex
- general polytopal classes:
-
ursachora
|
It shall be noted here, that the circumradius of the dual x-tet is sqrt(3/8) = 0.612372, while the inradius of the f-tet is sqrt[(3+sqrt(5))/48] = 0.330280.
Thus the augmentation tips well protrude beyond – even if the perspective chosen in the first lace city would suggest otherwise.
This then becomes visible also within the second lace city.
On the other hand, the second picture above kind of shows the green vertices and the yellow tet as spanning a cube. But this is not the case.
Rather those have a different height-coordinate, flattened by this perspective. In fact, the vertices of these 2 dual tet will span an hex.
Incidence matrix according to Dynkin symbol
xofo3ooox3oxoo&#xt → height(1,2) = 1/sqrt(8) = 0.353553
height(2,3) = height(3,4) = sqrt[3+sqrt(5)]/4 = 0.572061
(tet || pseudo dual tet || pseudo f-tet || oct)
o...3o...3o... | 4 * * * | 3 3 1 0 0 0 0 | 3 6 3 3 0 0 0 0 0 | 1 3 6 0 0 0 0
.o..3.o..3.o.. | * 4 * * ♦ 0 3 0 3 3 0 0 | 0 3 3 0 6 3 0 0 0 | 0 1 3 3 1 0 0
..o.3..o.3..o. | * * 4 * | 0 0 1 3 0 3 0 | 0 0 3 3 6 0 3 0 0 | 0 0 6 3 0 1 0
...o3...o3...o | * * * 6 | 0 0 0 0 2 2 4 | 0 0 0 1 4 4 4 2 2 | 0 0 2 4 2 2 1
-------------------+---------+--------------------+------------------------+----------------
x... .... .... | 2 0 0 0 | 6 * * * * * * | 2 2 0 1 0 0 0 0 0 | 1 2 2 0 0 0 0
oo..3oo..3oo..&#x | 1 1 0 0 | * 12 * * * * * | 0 2 1 0 0 0 0 0 0 | 0 1 2 0 0 0 0
o.o.3o.o.3o.o.&#x | 1 0 1 0 | * * 4 * * * * | 0 0 3 3 0 0 0 0 0 | 0 0 6 0 0 0 0
.oo.3.oo.3.oo.&#x | 0 1 1 0 | * * * 12 * * * | 0 0 1 0 2 0 0 0 0 | 0 0 2 1 0 0 0
.o.o3.o.o3.o.o&#x | 0 1 0 1 | * * * * 12 * * | 0 0 0 0 2 2 0 0 0 | 0 0 1 2 1 0 0
..oo3..oo3..oo&#x | 0 0 1 1 | * * * * * 12 * | 0 0 0 1 2 0 2 0 0 | 0 0 2 2 0 1 0
.... ...x .... | 0 0 0 2 | * * * * * * 12 | 0 0 0 0 0 1 1 1 1 | 0 0 0 1 1 1 1
-------------------+---------+--------------------+------------------------+----------------
x...3o... .... | 3 0 0 0 | 3 0 0 0 0 0 0 | 4 * * * * * * * * | 1 1 0 0 0 0 0
xo.. .... ....&#x | 2 1 0 0 | 1 2 0 0 0 0 0 | * 12 * * * * * * * | 0 1 1 0 0 0 0
ooo.3ooo.3ooo.&#x | 1 1 1 0 | 0 1 1 1 0 0 0 | * * 12 * * * * * * | 0 0 2 0 0 0 0
x.fo .... ....&#xt | 2 0 2 1 | 1 0 2 0 0 2 0 | * * * 6 * * * * * | 0 0 2 0 0 0 0
.ooo3.ooo3.ooo&#x | 0 1 1 1 | 0 0 0 1 1 1 0 | * * * * 24 * * * * | 0 0 1 1 0 0 0
.... .o.x ....&#x | 0 1 0 2 | 0 0 0 0 2 0 1 | * * * * * 12 * * * | 0 0 0 1 1 0 0
.... ..ox ....&#x | 0 0 1 2 | 0 0 0 0 0 2 1 | * * * * * * 12 * * | 0 0 0 1 0 1 0
...o3...x .... | 0 0 0 3 | 0 0 0 0 0 0 3 | * * * * * * * 4 * | 0 0 0 0 1 0 1
.... ...x3...o | 0 0 0 3 | 0 0 0 0 0 0 3 | * * * * * * * * 4 | 0 0 0 0 0 1 1
-------------------+---------+--------------------+------------------------+----------------
x...3o...3o... ♦ 4 0 0 0 | 6 0 0 0 0 0 0 | 4 0 0 0 0 0 0 0 0 | 1 * * * * * *
xo..3oo.. ....&#x ♦ 3 1 0 0 | 3 3 0 0 0 0 0 | 1 3 0 0 0 0 0 0 0 | * 4 * * * * *
xofo .... ....&#xr ♦ 2 1 2 1 | 1 2 2 2 1 2 0 | 0 1 2 1 2 0 0 0 0 | * * 12 * * * * cycle: (1342)
.... .oox ....&#x ♦ 0 1 1 2 | 0 0 0 1 2 2 1 | 0 0 0 0 2 1 1 0 0 | * * * 12 * * *
.o.o3.o.x ....&#x ♦ 0 1 0 3 | 0 0 0 0 3 0 3 | 0 0 0 0 0 3 0 1 0 | * * * * 4 * *
.... ..ox3..oo&#x ♦ 0 0 1 3 | 0 0 0 0 0 3 3 | 0 0 0 0 0 0 3 0 1 | * * * * * 4 *
...o3...x3...o ♦ 0 0 0 6 | 0 0 0 0 0 0 12 | 0 0 0 0 0 0 0 4 4 | * * * * * * 1
©
©