Acronym	tibbit
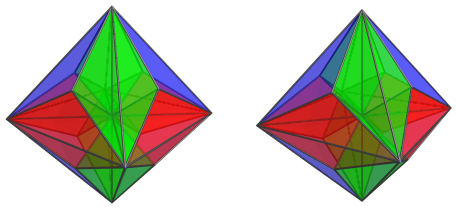
Name	triangular-bipyramidal triacontadichoron, rectified-tesseract dual, surtegmated hexadecachoron
	©
Inradius	1/sqrt(2) = 0.707107
Coordinates	(3, 0, 0, 0)/sqrt(18)     & all permutations, all changes of sign (1, 1, 1, 1)/sqrt(18)     & all permutations, all changes of sign
Dual	rit
Face vector	24, 88, 96, 32
External links

This polychoron can be obtained from the compound of a c = sqrt(2)/3 scaled tes and a dual unit-edged hex, thus choosing the edge center radius of tes and the triangle center radius of hex to be equal. The convex hull therefrom results in this polychoron, and the edges of the former resp. the orthogonal triangles of the latter will serve as diametrals of the cells of this hull polychoron, which are identical quite flat trigonal bipyramids co oo3ox&#zy.

Accordingly those c edges, provided in the below description, only qualify as pseudo edges wrt. the full polychoron.

Because o4m3o3o is derived by some secondary process only (rectification followed by dualisation), instead of a primary Wythoff construction, it is much more remarkable that it still allows for a true rectification (oa4oo3bo3oc&zx). This is because the truncational depth of the second vertex type (in the below incidence matrix) for a rectification scenario is easily settled at the second edge type (providing the mid points at those x-edges). But then the same truncational hyperplanes would define corresponding intersection points on the y-edges as well. And those points then could be matched in a rectificational sense by truncation hyperplanes of according depth wrt. the first vertex set.

Being the dual of rit and considering that one's coordinates, it is apparent that this solid is nothing but a hyperball wrt. the norm max(|x|+|y|+|z|, |x|+|y|+|w|, |x|+|z|+|w|, |y|+|z|+|w|).

Incidence matrix according to Dynkin symbol

o4m3o3o =
co4oo3oo3ox&#zy   → height = 0
                    c = sqrt(2)/3 = 0.471405
                    y = sqrt(7/18) = 0.623610

o.4o.3o.3o.     | 16 * ♦  4  0 |  6 |  4
.o4.o3.o3.o     |  * 8 ♦  8  6 | 24 | 12
----------------+------+-------+----+---
oo4oo3oo3oo&#y  |  1 1 | 64  * |  3 |  3
.. .. .. .x     |  0 2 |  * 24 |  4 |  4
----------------+------+-------+----+---
.. .. .. ox&#y  |  1 2 |  2  1 | 96 |  2
----------------+------+-------+----+---
co .. oo3ox&#zy ♦  2 3 |  6  3 |  6 | 32