| Acronym | idsid pixhi |
| Name | icositetra-diminished small disprismatohexacosihecatonicosachoron |
| Circumradius | 3+sqrt(5) = 5.236068 |
| Dihedral angles |
|
| Face vector | 1920, 5040, 4272, 1152 |
| Confer |
|

In the same way, as sadi was derived as an icositetrachoral diminishing of ex, idsid pixhi can be derived as an icositetrachoral diminishing of sidpixhi. The fundamental domain of sadi (i.e. the dual of teddi), which there clearly encompasses just a single vertex, here would encompass a complete doe. Therefore idsid pixhi clearly is no longer uniform (as weren't lots of the Johnson solids neither).
Sadi was diminished at 24 vertices. Idsid pixhi accordingly will be diminished at 24 does. In fact 24 doe-first caps will be chopped off. Any individual of those clearly is a doe || srid.
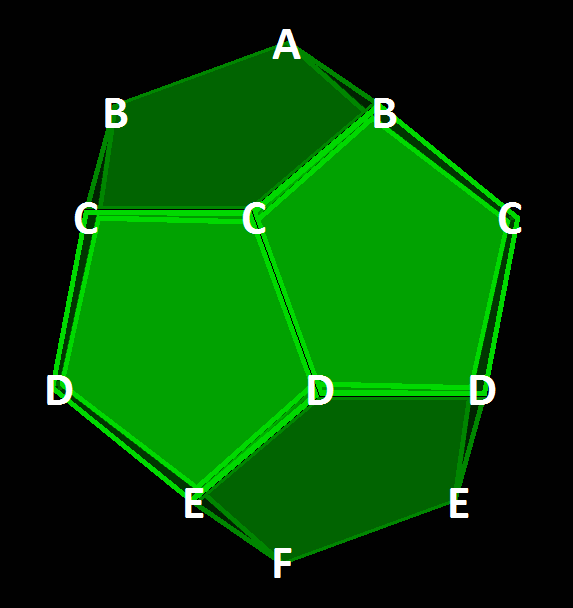
Corresponding to the 3-fold symmetry of that domain we call the vertices of doe as A, ..., F along its 3-fold axis. The other elements of idsid pixhi then can be classified accordingly, as given below. The prime denotes equivalent elements, mirrored at a domain face which is close to A. The hash is the same with respect to a domain face which is close to F. The remaining domain face mirror images are denoted by an asterisk.
A | 96 * * * * * | 3 0 0 0 0 0 0 3 0 0 0 0 0 | 3 0 0 0 0 6 0 0 0 0 0 3 0 0 0 | 1 0 3 0 0 3 0 1 0 B | * 288 * * * * | 1 2 0 0 0 0 0 0 2 0 1 0 0 | 0 1 2 0 0 2 2 0 2 0 0 2 1 0 0 | 0 1 1 2 0 2 1 1 0 C | * * 576 * * * | 0 1 1 1 0 0 0 0 0 1 0 1 0 | 0 0 0 1 0 0 1 1 1 1 0 1 1 1 0 | 0 0 0 1 0 1 1 1 1 D | * * * 576 * * | 0 0 0 1 1 1 0 0 0 0 0 0 2 | 0 0 0 0 1 0 0 0 0 2 2 0 1 1 1 | 0 0 0 0 1 0 2 1 1 E | * * * * 288 * | 0 0 0 0 0 2 1 0 0 0 0 2 0 | 0 0 0 1 0 0 0 0 2 2 0 0 0 1 2 | 0 0 0 1 0 0 2 1 1 F | * * * * * 96 | 0 0 0 0 0 0 3 0 0 0 3 0 0 | 0 0 3 0 0 0 0 0 6 0 0 0 0 0 3 | 0 1 0 3 0 0 3 1 0 --------+-----------------------+-----------------------------------------------------+-----------------------------------------------------------+------------------------------ AB | 1 1 0 0 0 0 | 288 * * * * * * * * * * * * | 0 0 0 0 0 2 0 0 0 0 0 2 0 0 0 | 0 0 1 0 0 2 0 1 0 BC | 0 1 1 0 0 0 | * 576 * * * * * * * * * * * | 0 0 0 0 0 0 1 0 1 0 0 1 1 0 0 | 0 0 0 1 0 1 1 1 0 CC | 0 0 2 0 0 0 | * * 288 * * * * * * * * * * | 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 | 0 0 0 0 0 1 0 1 1 CD | 0 0 1 1 0 0 | * * * 576 * * * * * * * * * | 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 | 0 0 0 0 0 0 1 1 1 DD | 0 0 0 2 0 0 | * * * * 288 * * * * * * * * | 0 0 0 0 0 0 0 0 0 0 2 0 1 0 1 | 0 0 0 0 1 0 2 1 0 DE | 0 0 0 1 1 0 | * * * * * 576 * * * * * * * | 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 | 0 0 0 0 0 0 1 1 1 EF | 0 0 0 0 1 1 | * * * * * * 288 * * * * * * | 0 0 0 0 0 0 0 0 2 0 0 0 0 0 2 | 0 0 0 1 0 0 2 1 0 AA' | 2 0 0 0 0 0 | * * * * * * * 144 * * * * * | 2 0 0 0 0 2 0 0 0 0 0 0 0 0 0 | 1 0 2 0 0 1 0 0 0 BB' | 0 2 0 0 0 0 | * * * * * * * * 288 * * * * | 0 1 1 0 0 1 1 0 0 0 0 0 0 0 0 | 0 1 1 1 0 1 0 0 0 CC' | 0 0 2 0 0 0 | * * * * * * * * * 288 * * * | 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 | 0 0 0 1 0 1 0 0 1 BB*&FF# | 0 1 0 0 0 1 | * * * * * * * * * * 288 * * | 0 0 2 0 0 0 0 0 2 0 0 0 0 0 0 | 0 1 0 2 0 0 1 0 0 CC*&EE# | 0 0 1 0 1 0 | * * * * * * * * * * * 576 * | 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 | 0 0 0 1 0 0 1 0 1 DD*&DD# | 0 0 0 2 0 0 | * * * * * * * * * * * * 576 | 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 | 0 0 0 0 1 0 1 0 1 --------+-----------------------+-----------------------------------------------------+-----------------------------------------------------------+------------------------------ AB | 3 0 0 0 0 0 | 0 0 0 0 0 0 0 3 0 0 0 0 0 | 96 * * * * * * * * * * * * * * | 1 0 1 0 0 0 0 0 0 AB' | 0 3 0 0 0 0 | 0 0 0 0 0 0 0 0 3 0 0 0 0 | * 96 * * * * * * * * * * * * * | 0 1 1 0 0 0 0 0 0 BC&EF' | 0 2 0 0 0 1 | 0 0 0 0 0 0 0 0 1 0 2 0 0 | * * 288 * * * * * * * * * * * * | 0 1 0 1 0 0 0 0 0 BC'&EF | 0 0 2 0 1 0 | 0 0 0 0 0 0 0 0 0 1 0 2 0 | * * * 288 * * * * * * * * * * * | 0 0 0 1 0 0 0 0 1 DD | 0 0 0 3 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 3 | * * * * 192 * * * * * * * * * * | 0 0 0 0 1 0 0 0 1 AB' | 2 2 0 0 0 0 | 2 0 0 0 0 0 0 1 1 0 0 0 0 | * * * * * 288 * * * * * * * * * | 0 0 1 0 0 1 0 0 0 BC' | 0 2 2 0 0 0 | 0 2 0 0 0 0 0 0 1 1 0 0 0 | * * * * * * 288 * * * * * * * * | 0 0 0 1 0 1 0 0 0 CC' | 0 0 4 0 0 0 | 0 0 2 0 0 0 0 0 0 2 0 0 0 | * * * * * * * 144 * * * * * * * | 0 0 0 0 0 1 0 0 1 BC*&EF# | 0 1 1 0 1 1 | 0 1 0 0 0 0 1 0 0 0 1 1 0 | * * * * * * * * 576 * * * * * * | 0 0 0 1 0 0 1 0 0 CD*&DE# | 0 0 1 2 1 0 | 0 0 0 1 0 1 0 0 0 0 0 1 1 | * * * * * * * * * 576 * * * * * | 0 0 0 0 0 0 1 0 1 DD*&DD# | 0 0 0 4 0 0 | 0 0 0 0 2 0 0 0 0 0 0 0 2 | * * * * * * * * * * 288 * * * * | 0 0 0 0 1 0 1 0 0 ABC | 1 2 2 0 0 0 | 2 2 1 0 0 0 0 0 0 0 0 0 0 | * * * * * * * * * * * 288 * * * | 0 0 0 0 0 1 0 1 0 BCD | 0 1 2 2 0 0 | 0 2 0 2 1 0 0 0 0 0 0 0 0 | * * * * * * * * * * * * 288 * * | 0 0 0 0 0 0 1 1 0 CDE | 0 0 2 2 1 0 | 0 0 1 2 0 2 0 0 0 0 0 0 0 | * * * * * * * * * * * * * 288 * | 0 0 0 0 0 0 0 1 1 DEF | 0 0 0 2 2 1 | 0 0 0 0 1 2 2 0 0 0 0 0 0 | * * * * * * * * * * * * * * 288 | 0 0 0 0 0 0 1 1 0 --------+-----------------------+-----------------------------------------------------+-----------------------------------------------------------+------------------------------ A ♦ 4 0 0 0 0 0 | 0 0 0 0 0 0 0 6 0 0 0 0 0 | 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 24 * * * * * * * * B&F ♦ 0 3 0 0 0 1 | 0 0 0 0 0 0 0 0 3 0 3 0 0 | 0 1 3 0 0 0 0 0 0 0 0 0 0 0 0 | * 96 * * * * * * * AB ♦ 3 3 0 0 0 0 | 3 0 0 0 0 0 0 3 3 0 0 0 0 | 1 1 0 0 0 3 0 0 0 0 0 0 0 0 0 | * * 96 * * * * * * BC&EF ♦ 0 2 2 0 1 1 | 0 2 0 0 0 0 1 0 1 1 2 2 0 | 0 0 1 1 0 0 1 0 2 0 0 0 0 0 0 | * * * 288 * * * * * DD ♦ 0 0 0 6 0 0 | 0 0 0 0 3 0 0 0 0 0 0 0 6 | 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 | * * * * 96 * * * * ABC ♦ 2 4 4 0 0 0 | 4 4 2 0 0 0 0 1 2 2 0 0 0 | 0 0 0 0 0 2 2 1 0 0 0 2 0 0 0 | * * * * * 144 * * * BCD&DEF ♦ 0 1 2 4 2 1 | 0 2 0 2 2 2 2 0 0 0 1 2 2 | 0 0 0 0 0 0 0 0 2 2 1 0 1 0 1 | * * * * * * 288 * * doe ♦ 1 3 6 6 3 1 | 3 6 3 6 3 6 3 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 3 3 3 3 | * * * * * * * 96 * srid ♦ 0 0 24 24 12 0 | 0 0 12 24 0 24 0 0 0 12 0 24 24 | 0 0 0 12 8 0 0 6 0 24 0 0 0 12 0 | * * * * * * * * 24
© 2004-2026 | top of page |