Acronym	gittith
Name	great tesseractitesseractihexadecachoron
Cross sections	©
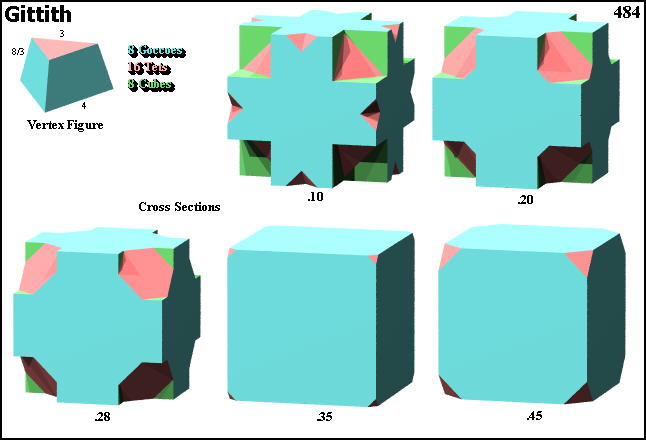Circumradius	sqrt[(3-sqrt(2))/2] = 0.890446
Inradius wrt. tet	[2 sqrt(2)-1]/sqrt(8) = 0.646447
Inradius wrt. gocco	1/2 = 0.5
Inradius wrt. cube	(sqrt(2)-1)/2 = 0.207107
Coordinates	((sqrt(2)-1)/2, 1/2, 1/2, 1/2)   & all permutations, all changes of sign
Volume	[24 sqrt(2)-19]/6 = 2.490188
Surface	[68 sqrt(2)-24]/3 = 24.055507
General of army	tat
Colonel of regiment	(is itself locally convex – uniform polychoral members: by cells: cube gocco groh querco stop tet trip quidpith 32 0 0 0 0 16 32 picnut 24 8 0 0 0 0 32 gittifcoth 24 0 0 8 0 16 0 gaquipadah 16 0 0 0 8 16 32 gittith 8 8 0 0 0 16 0 gahfipto 8 0 0 8 0 0 32 gnappoth 0 0 8 0 0 16 32 & others)
Dihedral angles (at margins)	at {3} between gocco and tet:   120° at {4} between cube and gocco:   90° at {8/3} between gocco and gocco:   90°
Face vector	64, 192, 136, 32
Confer	general polytopal classes: Wythoffian polychora   analogs: gocco series
External links

As abstract polytope gittith is isomorphic to steth, thereby replacing octagrams by octagons, resp. gocco by socco.

Incidence matrix according to Dynkin symbol

     o    
   3 |    
     o    
  3 / \ 4 
   x---x  
    4/3   

o3o3x4/3x4*b

. . .   .    | 64 |  3  3 |  3  3  3 |  1 1 3
-------------+----+-------+----------+-------
. . x   .    |  2 | 96  * |  2  0  1 |  1 0 2
. . .   x    |  2 |  * 96 |  0  2  1 |  0 1 2
-------------+----+-------+----------+-------
. o3x   .    |  3 |  3  0 | 64  *  * |  1 0 1
. o .   x4*b |  4 |  0  4 |  * 48  * |  0 1 1
. . x4/3x    |  8 |  4  4 |  *  * 24 |  0 0 2
-------------+----+-------+----------+-------
o3o3x   .    ♦  4 |  6  0 |  4  0  0 | 16 * *
o3o .   x4*b ♦  8 |  0 12 |  0  6  0 |  * 8 *
. o3x4/3x4*b ♦ 24 | 24 24 |  8  6  6 |  * * 8

     o     
   3 |     
     o     
3/2 / \ 4/3
   x---x   
    4/3    

o3o3/2x4/3x4/3*b

. .   .   .      | 64 |  3  3 |  3  3  3 |  1 1 3
-----------------+----+-------+----------+-------
. .   x   .      |  2 | 96  * |  2  0  1 |  1 0 2
. .   .   x      |  2 |  * 96 |  0  2  1 |  0 1 2
-----------------+----+-------+----------+-------
. o3/2x   .      |  3 |  3  0 | 64  *  * |  1 0 1
. o   .   x4/3*b |  4 |  0  4 |  * 48  * |  0 1 1
. .   x4/3x      |  8 |  4  4 |  *  * 24 |  0 0 2
-----------------+----+-------+----------+-------
o3o3/2x   .      ♦  4 |  6  0 |  4  0  0 | 16 * *
o3o   .   x4/3*b ♦  8 |  0 12 |  0  6  0 |  * 8 *
. o3/2x4/3x4/3*b ♦ 24 | 24 24 |  8  6  6 |  * * 8

     o    
 3/2 |    
     o    
  3 / \ 4 
   x---x  
    4/3   

o3/2o3x4/3x4*b

.   . .   .    | 64 |  3  3 |  3  3  3 |  1 1 3
---------------+----+-------+----------+-------
.   . x   .    |  2 | 96  * |  2  0  1 |  1 0 2
.   . .   x    |  2 |  * 96 |  0  2  1 |  0 1 2
---------------+----+-------+----------+-------
.   o3x   .    |  3 |  3  0 | 64  *  * |  1 0 1
.   o .   x4*b |  4 |  0  4 |  * 48  * |  0 1 1
.   . x4/3x    |  8 |  4  4 |  *  * 24 |  0 0 2
---------------+----+-------+----------+-------
o3/2o3x   .    ♦  4 |  6  0 |  4  0  0 | 16 * *
o3/2o .   x4*b ♦  8 |  0 12 |  0  6  0 |  * 8 *
.   o3x4/3x4*b ♦ 24 | 24 24 |  8  6  6 |  * * 8

     o     
 3/2 |     
     o     
3/2 / \ 4/3
   x---x   
    4/3    

o3/2o3/2x4/3x4/3*b

.   .   .   .      | 64 |  3  3 |  3  3  3 |  1 1 3
-------------------+----+-------+----------+-------
.   .   x   .      |  2 | 96  * |  2  0  1 |  1 0 2
.   .   .   x      |  2 |  * 96 |  0  2  1 |  0 1 2
-------------------+----+-------+----------+-------
.   o3/2x   .      |  3 |  3  0 | 64  *  * |  1 0 1
.   o   .   x4/3*b |  4 |  0  4 |  * 48  * |  0 1 1
.   .   x4/3x      |  8 |  4  4 |  *  * 24 |  0 0 2
-------------------+----+-------+----------+-------
o3/2o3/2x   .      ♦  4 |  6  0 |  4  0  0 | 16 * *
o3/2o   .   x4/3*b ♦  8 |  0 12 |  0  6  0 |  * 8 *
.   o3/2x4/3x4/3*b ♦ 24 | 24 24 |  8  6  6 |  * * 8